感知機和神經網絡

引入?

什么是神經網絡？

我們今天學習的神經網絡，不是人或動物的神經網絡，但是又是模仿人和動物的神經網絡而定制的神經系統，特別是大腦和神經中樞，定制的系統是一種數學模型或計算機模型，神經網絡由大量的人工神經元連接而成，大多數時候人工神經網絡能夠在外界信息的基礎上改變內部結構，是一種自適應的改變的過程，現代的神經網絡是一種基于傳統統計學的建模工具，常用來對輸入和輸出之間復雜的關系進行建模或者探索數據之間的模式

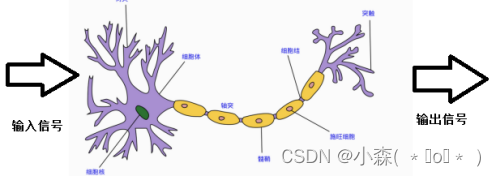
人或動物的神經元如下，當人感受到刺激的時候，信號會通過傳道部傳遞信號，最后會作用在效應部做出相應的反應。神經網絡是一種運算模型，有大量的節點，神經元節點之間構成了聯系，這些神經元負責傳遞信息和加工信息，神經元可以被訓練和強化，形成一種固定的形態，對一些特殊的信息會有更強烈的反應。

這張圖片是一張古風女士的圖片，因為在我們的生活中的經驗已經告訴我們人的模樣，椅子的樣子，衣服的模樣。

所以通過我們強大的成熟的視覺神經系統判定她是一個古風女孩。

計算機系統和人腦一樣，也是通過不斷訓練，告訴計算機那些是貓，那些是狗，會通過一個數學模型來得到結果。比如：百度圖片搜索就能識別圖片的物體，地點以及其他信息，都歸功于計算機神經系統的突破發展。

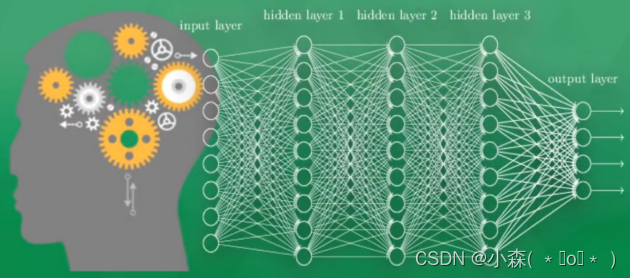
一個可視化的神經網絡系統，由多層的神經元組成，為了區分不同的神經層，我們通常將輸入信息的叫做輸入層，中間傳遞信息叫做隱藏層或隱層，輸出層就是將前面傳遞的信息形成輸出的結果，通過該結果能直接看到計算機對物體的認知，隱層通常由1層或多層組成，負責輸入層的加工信息的處理，類似于人類的神經系統，通過多層的神經加工才能達到最后的效果。

?一個可視化的神經網絡系統，由多層的神經元組成，為了區分不同的神經層，我們通常將輸入信息的叫做輸入層，中間傳遞信息叫做隱藏層或隱層，輸出層就是將前面傳遞的信息形成輸出的結果，通過該結果能直接看到計算機對物體的認知，隱層通常由1層或多層組成，負責輸入層的加工信息的處理，類似于人類的神經系統，通過多層的神經加工才能達到最后的效果。

現在的深度學習就是從神經網絡發展而來，當神經網絡中間的隱層非常之多的時候可處理的信息也會非常之多，這也是叫深度神經網絡的原因。當隱藏層只有1個時候，是神經網絡中的“BP神經網絡”模型，而沒有隱層，只有輸入輸出層的是最簡單的“感知機”分類模型。

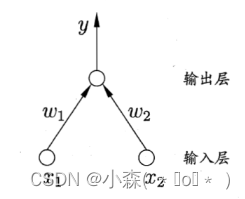
感知機由輸入層和輸出層組成，沒有隱藏層。它接收多個輸入信號，通過加權求和后，如果超過某個閾值，則輸出一個信號，這種結構使其成為一個線性分類器。
感知機通過錯誤修正算法來更新權重。當模型做出錯誤預測時，它會調整權重以減少未來的錯誤。

感知機作為神經網絡的基礎，雖然簡單，但為理解更復雜的神經網絡模型提供了重要的起點。?

通常計算機能看到的和處理的和人類會有很大的不同，比如圖片和聲音、文字，他們在計算機中均已0或1的方式存在再神經網絡中，通過對這一些0-1數字的加工和處理生成另外一些數字，而生成的數字也有了物理上的意義了。

神經網絡訓練的過程

首先，需要準備大量的數據集，進行上千萬次的訓練，但是計算機不一定能識別正確，比如一張圖原來是貓的被識別成了狗，雖然識別錯誤了，但是這個錯誤是非常有價值的，我們可以從這次錯誤中總結和學習經驗，計算機一般是根據正確的答案和預測的答案做對比產生一個差別，在將這個差別反向傳遞回去，每一個神經元往正確的方向上改動一點點，這樣下一次識別的時候，通過已經改進的神經網絡識別的正確率會提高一些，將每次一點點的提高加上上千萬次的訓練，最終的識別效果也就被提高了，最后到了驗收結果的時候原來是貓現在也被識別為貓。

計算機中的每個神經元都有屬于他的激勵函數，我們可以利用這些函數給計算機一個刺激行為。

當第一次給計算機看貓的圖片的時候，只有部分神經元被激勵或激活，被激活的神經元會傳遞給下一級別的神經元，這些傳遞的信息也是計算機中最為重要的信息，也就是對輸出結果最優價值的信息，如果預測成了狗狗，那么神經元的一些參數就會被調整，有一些神經元變得遲鈍，有一些則變得敏感起來，這就說明所有神經元參數都在被改變，往識別正確的方向去改變了，被改動的參數也能逐漸的預測出正確的答案，這就是神經網絡的過程。???

感知機

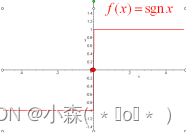
感知機只有輸出層神經元進行激活函數處理，即只擁有一層功能神經元，學習能力非常有限，感知機的學習皆在求將訓練數據進行線性劃分的分離超平面。為此，導入基于誤分類的損失函數，利用梯度下降法對損失函數進行極小化，求得感知機模型。?

激勵函數

BP神經網絡

BP中采用的梯度求解最優參數的方法是最常用的方法，但是如果誤差函數在當前點的梯度為0，已達到了局部最小，更新量將為0，這意味著迭代將會停止，但此時如果誤差函數僅僅有一個局部的最小，那么此時的局部最小將變為全局最小；如果誤差函數有多個局部最小，則不能保證找到的解釋全部最小，這種情形也是參數陷入局部最小的情況。

以不同的參數值初始化多個網絡，按不同方法標準化訓練后，取最小的解作為最終參數。這相當于從多個不同的初始點開始搜索，這樣就可能陷入不同的局部最小，從中選擇可能更接近全局最小的結果。
使用“模擬退火”技術在每一步都以一定的概率接受比當前更差的結果，從而有助于跳出局部最小。在每次迭代的過程中，接受“次優解”的概率要隨著時間的推移而逐漸降低，從而保證算法的穩定性。
使用隨機梯度下降。與標準的梯度下降算法精確計算梯度不同。隨機梯度下降法在計算梯度的時候加入了隨機因素。即便陷入了局部最小值點，它計算的梯度仍不可能為0，這樣就跳出了局部最小搜索。

梯度下降法

找到一個拋物線的最低點：

首先求導，令導數為0，求值。l為學習率，為（0,1]的值，設置的小，需要很長時間才能到最低點。設置的大，可能錯過最低點。一般設置的時候首先設置的大一些，等到快接近最低點步子放慢一些。

import numpy as np
def tanh(x): ?return np.tanh(x)def tanh_deriv(x): ?return 1.0 - np.tanh(x)*np.tanh(x)def logistic(x): ?return 1/(1 + np.exp(-x))def logistic_derivative(x): ?return logistic(x)*(1-logistic(x))class NeuralNetwork: ??def __init__(self, layers, activation='tanh'): ?""" ?:param layers: A list containing the number of units in each layer.Should be at least two values ?:param activation: The activation function to be used. Can be"logistic" or "tanh" ?""" ?if activation == 'logistic': ?self.activation = logistic ?self.activation_deriv = logistic_derivative ?elif activation == 'tanh': ?self.activation = tanh ?self.activation_deriv = tanh_derivself.weights = [] ?for i in range(1, len(layers) - 1): ?self.weights.append((2*np.random.random((layers[i - 1] + 1, layers[i] + 1))-1)*0.25) ?self.weights.append((2*np.random.random((layers[i] + 1, layers[i + 1]))-1)*0.25) ? ??def fit(self, X, y, learning_rate=0.2, epochs=10000): ? ? ? ??X = np.atleast_2d(X) ? ? ? ??temp = np.ones([X.shape[0], X.shape[1]+1]) ? ? ? ??temp[:, 0:-1] = X ?# adding the bias unit to the input layer ? ? ? ??X = temp ? ? ? ??from NeuralNetwork import NeuralNetwork
import numpy as npnn = NeuralNetwork([2,2,1], 'tanh') ? ??
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) ? ??
y = np.array([0, 1, 1, 0]) ? ??
nn.fit(X, y) ? ??
for i in [[0, 0], [0, 1], [1, 0], [1,1]]: ? ?print(i, nn.predict(i))