基于混合注意力網絡和深度信念網絡的魯棒視頻水印技術基礎理論深度解析

1. 引言

隨著數字媒體技術的迅猛發展和互聯網的普及，視頻內容的創作、傳播和分享變得前所未有的便捷。然而，這種便利性也帶來了嚴重的版權保護挑戰。數字視頻的易復制性使得盜版和非法傳播成為困擾內容創作者和版權所有者的重大問題。傳統的加密技術雖然能夠在一定程度上保護數字內容，但一旦內容被解密，就失去了進一步的保護能力。在這種背景下，數字水印技術作為一種新興的版權保護手段應運而生，它能夠將版權信息直接嵌入到數字媒體內容中，實現對數字內容的持久性保護。

數字水印技術的核心思想是在不影響原始內容感知質量的前提下，將特定的標識信息（水印）隱藏在數字媒體中。這些水印信息在正常的觀看或使用過程中是不可見或不可感知的，但可以通過特定的算法和密鑰提取出來，從而實現對數字內容的版權認證、完整性驗證和來源追溯。與傳統的版權保護方法相比，數字水印技術具有隱蔽性強、魯棒性好、容量大等優勢，已經成為數字版權保護領域的重要技術手段。

視頻水印作為數字水印技術的重要分支，面臨著比圖像水印更為復雜的技術挑戰。視頻數據不僅具有空間維度的特征，還包含時間維度的信息，這使得視頻水印需要在空域、頻域和時域等多個維度上進行考慮。同時，視頻在傳輸和存儲過程中可能遭受各種有意或無意的攻擊，如壓縮、噪聲添加、幾何變換、幀操作等，這要求視頻水印算法必須具備足夠的魯棒性來抵抗這些攻擊。

近年來，深度學習技術的快速發展為數字水印領域帶來了新的機遇和挑戰。基于深度學習的水印方法能夠自動學習數據的深層特征表示，實現更加智能和自適應的水印嵌入和提取策略。特別是注意力機制的引入，使得水印算法能夠動態地關注視頻內容中最重要的區域，從而在保證不可感知性的同時提高魯棒性。

論文《DeepSecure watermarking: Hybrid Attention on Attention Net and Deep Belief Net based robust video authentication using Quaternion Curvelet Transform domain》提出了一種創新的視頻水印方法，該方法巧妙地融合了多種先進技術，包括注意力機制（Attention Mechanism）、深度信念網絡（Deep Belief Network）、四元數曲波變換（Quaternion Curvelet Transform）以及黃金分割斐波那契樹優化算法（Golden Section Fibonacci Tree Optimization）。這種多技術融合的方法在視頻水印的不可感知性和魯棒性之間實現了良好的平衡，為視頻版權保護提供了新的技術路徑。

2. 數字水印技術基礎理論

2.1 數字水印的基本概念與分類

數字水印技術起源于物理世界中的紙質水印概念，但其內涵和外延都得到了極大的擴展。從技術角度來看，數字水印是一種信息隱藏技術，它將特定的數字信號（水印）嵌入到數字媒體載體中，使得水印信息與載體內容緊密結合，難以被分離或篡改。這種嵌入過程需要滿足兩個基本要求：一是不可感知性（Imperceptibility），即水印的嵌入不應該明顯影響載體的感知質量；二是魯棒性（Robustness），即水印信息應該能夠抵抗各種可能的攻擊和處理操作。

根據水印嵌入的域空間不同，數字水印技術可以分為空域水印和變換域水印兩大類。空域水印直接在像素層面進行操作，通過修改圖像或視頻幀的像素值來嵌入水印信息。最典型的空域水印方法是最低有效位（Least Significant Bit, LSB）方法，它將水印信息替換載體圖像的最低有效位。LSB方法的優點是實現簡單、嵌入容量大，但缺點是魯棒性較差，容易受到各種信號處理操作的影響。另一種常見的空域方法是疊加法，它將水印信號與載體信號直接相加，數學表達式為：

$I_w(x,y) = I(x,y) + \alpha \cdot W(x,y)$

其中 $I(x,y)$ 表示原始載體圖像， $W(x,y)$ 表示水印信號， $\alpha$ 表示嵌入強度因子， $I_w(x,y)$ 表示嵌入水印后的圖像。

變換域水印則是在頻域中進行水印嵌入，它首先將載體信號通過某種數學變換轉換到頻域，然后在變換系數中嵌入水印信息，最后通過逆變換得到嵌入水印的載體信號。常用的變換包括離散余弦變換（DCT）、離散小波變換（DWT）、離散傅里葉變換（DFT）等。變換域水印的主要優勢在于其良好的魯棒性，因為頻域系數通常對常見的信號處理操作（如壓縮、濾波等）具有更強的抗干擾能力。例如，在DCT域中的水印嵌入可以表示為：

$C_w(u,v) = C(u,v) + \alpha \cdot W(u,v)$

其中 $C(u,v)$ 表示原始DCT系數， $W(u,v)$ 表示水印信號在DCT域的表示， $C_w(u,v)$ 表示嵌入水印后的DCT系數。

2.2 視頻水印的特殊挑戰

與靜態圖像相比，視頻水印面臨著更多的技術挑戰。首先，視頻具有時間維度，這使得水印算法需要考慮幀間的相關性和時間一致性。視頻中相鄰幀之間往往存在很強的相關性，這種相關性既可以被利用來提高水印的魯棒性，也可能成為攻擊者利用的弱點。其次，視頻數據量龐大，對算法的計算效率提出了更高的要求。一個典型的高清視頻文件可能包含數十萬幀圖像，如果對每一幀都進行復雜的水印處理，將會帶來巨大的計算開銷。

視頻在傳輸和存儲過程中還可能遭受各種特有的攻擊，包括時域攻擊和空域攻擊。時域攻擊主要針對視頻的時間特性，如幀丟棄（Frame Dropping）、幀重排（Frame Reordering）、幀插入（Frame Insertion）等。這些攻擊會破壞視頻的時間結構，可能導致基于時間相關性的水印信息丟失。空域攻擊則包括傳統的圖像處理攻擊，如噪聲添加、濾波、幾何變換等，以及視頻特有的壓縮攻擊。視頻壓縮是視頻處理中最常見的操作，不同的壓縮標準（如H.264、H.265等）采用不同的壓縮算法，這些算法可能會顯著影響嵌入的水印信息。

為了應對這些挑戰，視頻水印算法通常采用關鍵幀（Key Frame）選擇策略，即只在視頻的關鍵幀中嵌入水印信息。關鍵幀的選擇需要考慮多個因素，包括幀的重要性、視覺顯著性、運動信息等。數學上，關鍵幀的選擇可以建模為一個優化問題：

$\arg\max_{F \subset {f_1, f_2, ..., f_N}} \sum_{f_i \in F} \text{Importance}(f_i)$

其中 ${f_1, f_2, ..., f_N}$ 表示視頻中的所有幀，F表示選擇的關鍵幀集合， $\text{Importance}(f_i)$ 表示第 $i$ 幀的重要性度量。

2.3 水印系統的性能評價指標

數字水印系統的性能通常通過多個指標來評價，這些指標反映了水印算法在不可感知性、魯棒性、安全性等方面的表現。不可感知性是衡量水印嵌入對載體質量影響程度的指標，常用的客觀評價指標包括峰值信噪比（Peak Signal-to-Noise Ratio, PSNR）和結構相似性指數（Structural Similarity Index, SSIM）。PSNR的計算公式為：

$\text{PSNR} = 10 \log_{10} \frac{\text{MAX}^2}{\text{MSE}}$

其中MAX表示圖像可能的最大像素值，MSE表示均方誤差：

$\text{MSE} = \frac{1}{MN} \sum_{i=0}^{M-1} \sum_{j=0}^{N-1} [I(i,j) - I_w(i,j)]^2$

SSIM指標考慮了人眼視覺系統的特性，通過比較亮度、對比度和結構信息來評價圖像質量：

$\text{SSIM}(x,y) = \frac{(2\mu_x\mu_y + c_1)(2\sigma_{xy} + c_2)}{(\mu_x^2 + \mu_y^2 + c_1)(\sigma_x^2 + \sigma_y^2 + c_2)}$

其中 $\mu_x,\mu_y$ 分別表示圖像x和y的均值， $\sigma_x^2,\sigma_y^2$ 分別表示方差， $\sigma_{xy}$ 表示協方差， $c_1,c_2$ 為常數。

魯棒性評價主要關注水印在各種攻擊下的生存能力，常用指標包括歸一化相關系數（Normalized Correlation Coefficient, NCC）和誤碼率（Bit Error Rate, BER）。NCC用于衡量提取水印與原始水印之間的相似度：

$\text{NCC} = \frac{\sum_{i=1}^{N} W_i \cdot W'i}{\sqrt{\sum{i=1}^{N} W_i^2} \sqrt{\sum_{i=1}^{N} W'^2_i}}$

其中 $W_i$ 表示原始水印的第i個元素， $W'_i$ 表示提取水印的第i個元素。BER則計算錯誤提取的比特數占總比特數的比例：

3. 注意力機制的基礎原理

3.1 注意力機制的生物學啟發與數學基礎

注意力機制源于對人類認知過程的模擬，特別是人類視覺注意力系統的工作原理。在日常生活中，人類面對復雜的視覺場景時，并不會同時關注所有的細節，而是會選擇性地將注意力集中在最重要或最相關的信息上。這種選擇性注意的能力使得人類能夠在有限的認知資源下高效地處理大量信息。心理學研究表明，人類的注意力機制包括自下而上（bottom-up）和自上而下（top-down）兩種模式。自下而上的注意力由刺激的顯著性驅動，而自上而下的注意力則由任務目標和先驗知識引導。

在深度學習中，注意力機制的數學基礎可以追溯到信息論和概率論。從信息論的角度來看，注意力機制可以理解為一種信息選擇和過濾機制，它通過分配不同的權重來突出重要信息，抑制不相關信息。數學上，注意力機制可以表示為一個加權平均的過程：

$\text{Attention}(Q, K, V) = \sum_{i=1}^{n} \alpha_i v_i$

其中Q表示查詢（Query），K表示鍵（Key），V表示值（Value）， $\alpha_i$ 表示注意力權重， $v_i$ 表示第i個值向量。注意力權重 $\alpha_i$ 的計算通常涉及查詢和鍵之間的相似度計算：

$\alpha_i = \frac{\exp(f(q, k_i))}{\sum_{j=1}^{n} \exp(f(q, k_j))}$

其中 $f(q, k_i)$ 表示查詢q與第i個鍵 $k_i$ 之間的相似度函數，常用的相似度函數包括點積、加性注意力、多層感知機等。

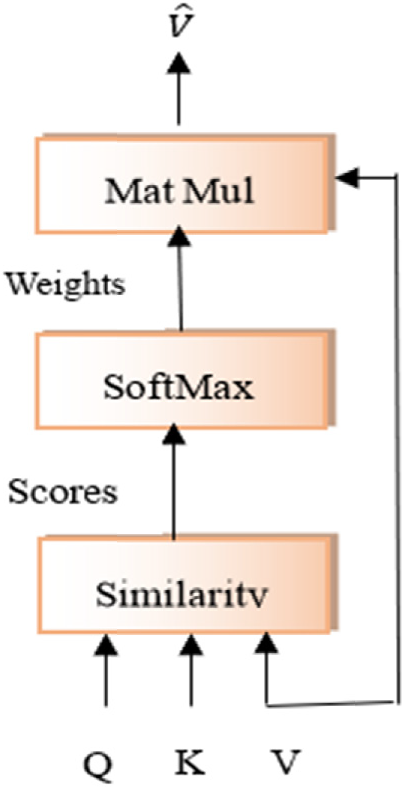
3.2 Scaled Dot-Product Attention的數學原理

Scaled Dot-Product Attention是最常用的注意力計算方法，它使用向量點積來計算查詢和鍵之間的相似度。點積操作的幾何意義是計算兩個向量之間的夾角余弦，當兩個向量方向相似時，點積值較大，表示較高的相關性。Scaled Dot-Product Attention的完整計算公式為：

$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$

其中 $d_k$ 表示鍵向量的維度，除以 $\sqrt{d_k}$ 的目的是進行縮放，防止點積結果過大導致softmax函數進入飽和區域。這種縮放的必要性可以從統計學角度來理解：假設Q和K的元素是獨立的隨機變量，均值為0，方差為1，那么它們的點積的方差為 $d_k$ 。通過除以 $\sqrt{d_k}$ ，可以使得縮放后的點積具有單位方差，從而穩定訓練過程。

softmax函數將注意力分數轉換為概率分布：

$\text{softmax}(x_i) = \frac{\exp(x_i)}{\sum_{j=1}^{n} \exp(x_j)}$

這確保了所有注意力權重的和為1，符合概率分布的定義。從信息論的角度來看，softmax函數實現了一種"軟選擇"機制，相比于硬性的最大值選擇，軟選擇能夠保留更多的信息，有利于梯度的反向傳播。

3.3 多頭注意力機制的并行處理能力

多頭注意力（Multi-Head Attention）是對單頭注意力的擴展，它并行計算多個注意力頭，每個頭關注輸入的不同方面。這種設計的理論基礎來自于集成學習的思想，多個弱學習器的組合往往能夠獲得比單個強學習器更好的性能。在注意力機制中，不同的頭可以學習到不同類型的依賴關系，如短距離依賴、長距離依賴、句法依賴、語義依賴等。

多頭注意力的數學表達式為：

$\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, ..., \text{head}_h)W^O$

其中每個注意力頭的計算為：

$\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)$

這里 $W_i^Q \in \mathbb{R}^{d_{model} \times d_k},W_i^K \in \mathbb{R}^{d_{model} \times d_k},W_i^V \in \mathbb{R}^{d_{model} \times d_v}$ 是可學習的投影矩陣， $W^O \in \mathbb{R}^{hd_v \times d_{model}}$ 是輸出投影矩陣。通過這些投影矩陣，不同的頭可以學習到輸入在不同子空間中的表示。

多頭注意力的一個重要優勢是計算的并行性。由于不同頭之間的計算相互獨立，可以在現代GPU架構上高效地并行執行。這種并行性不僅提高了計算效率，還增強了模型的表達能力。理論分析表明，多頭注意力能夠捕獲輸入序列中的多種模式和關系，其表達能力隨著頭數的增加而增強，但存在邊際遞減效應。

3.4 自注意力機制的長距離依賴建模

自注意力（Self-Attention）是注意力機制的一個特殊情況，其中查詢、鍵和值都來自同一個輸入序列。自注意力的核心優勢在于能夠直接建模序列中任意兩個位置之間的依賴關系，而不受距離限制。這與傳統的循環神經網絡（RNN）形成鮮明對比，RNN需要逐步傳遞信息，對于長距離依賴的建模能力有限。

自注意力機制的計算復雜度為 $O(n^2 d)$ ，其中n是序列長度，d是特征維度。雖然這種二次復雜度在長序列上可能成為瓶頸，但對于中等長度的序列，自注意力的并行性和建模能力使其成為理想的選擇。更重要的是，自注意力的權重矩陣提供了序列中不同位置之間關系的直觀可視化，這對于理解模型的行為具有重要價值。

在數學上，自注意力可以看作是輸入序列的一種自適應重新組合。對于輸入序列 $X = [x_1, x_2, ..., x_n]$ ，自注意力的輸出為：

$Y = \text{SelfAttention}(X) = \text{softmax}\left(\frac{XX^T}{\sqrt{d}}\right)X$

這個公式展現了自注意力的本質：首先計算序列中每對元素的相似度（ $XX^T$ ），然后將這些相似度作為權重，對原始序列進行加權組合。這種機制使得每個輸出位置都能夠"看到"輸入序列的全局信息，從而實現了全局上下文的有效建模。

4. Attention on Attention網絡的深度解析

4.1 傳統注意力機制的局限性分析

傳統的注意力機制雖然在許多任務中取得了顯著的成功，但仍然存在一些固有的局限性。其中最主要的問題是注意力機制的"盲目性"，即無論輸入的相關性如何，注意力機制總是會產生一個歸一化的權重分布。這意味著即使輸入中沒有相關信息，注意力機制仍然會強制分配權重，可能導致不相關信息被錯誤地納入最終表示中。這種現象在信息檢索和問答系統中尤為明顯，當查詢與所有候選項都不相關時，傳統注意力機制仍然會選擇"最不相關"的項作為答案。

從數學角度分析，傳統注意力機制的輸出可以表示為：

$c = \sum_{i=1}^{n} \alpha_i v_i, \quad \sum_{i=1}^{n} \alpha_i = 1$

由于softmax函數的歸一化特性，權重 $\alpha_i$ 總是非負且和為1。這意味著輸出c始終是輸入值 $v_i$ 的凸組合，無法表示"無相關信息"的情況。在實際應用中，這可能導致模型學習到虛假的相關性，特別是在訓練數據存在噪聲或標注錯誤的情況下。

另一個重要的局限性是傳統注意力機制缺乏對注意力質量的評估能力。在人類認知中，注意力不僅涉及"關注什么"，還包括"關注程度"的控制。例如，當面對模糊或不確定的刺激時，人類會調節注意力的強度，而不是盲目地分配最大注意力。傳統的注意力機制缺乏這種自適應調節能力，可能在處理低質量或不確定輸入時產生過擬合現象。

4.2 AoA網絡的設計理念與創新點

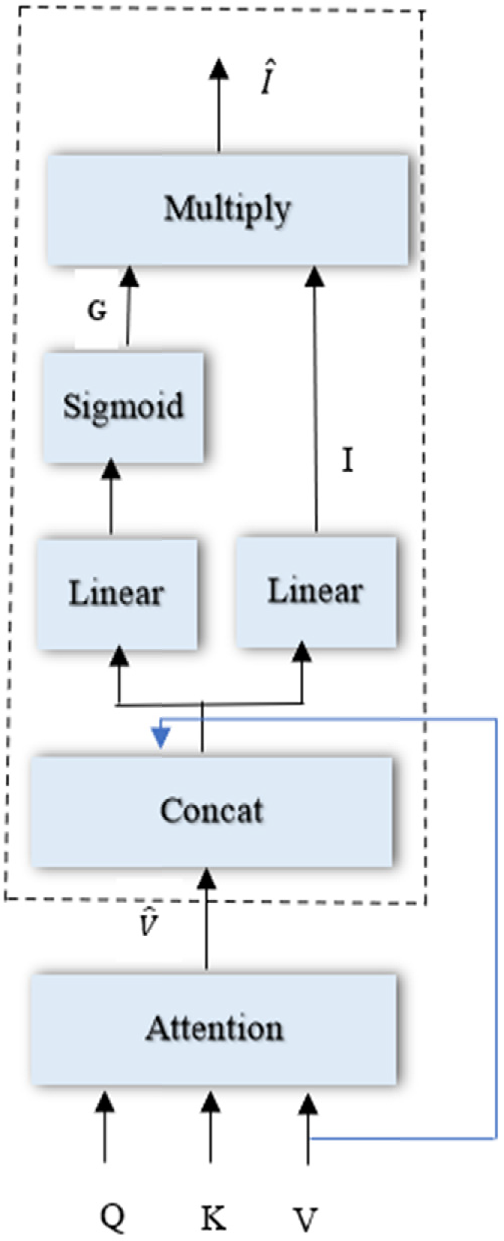
Attention on Attention（AoA）網絡的核心思想是在傳統注意力機制的基礎上增加一個"注意力門控"機制，用于控制注意力信息的流動。這種設計受到了門控機制在循環神經網絡中成功應用的啟發，如LSTM和GRU中的遺忘門、輸入門等。AoA網絡通過引入注意力門控，使得模型能夠自適應地決定是否以及在多大程度上使用注意力信息。

AoA網絡的數學模型包含兩個關鍵組件：信息向量（Information Vector）和注意力門控（Attention Gate）。信息向量$i$通過線性變換生成，包含了當前上下文的豐富信息：

$i = W_q^i Q + W_v^i \hat{V} + b^i$

其中Q表示查詢， $\hat{V}$ 表示傳統注意力機制的輸出， $W_q^i,W_v^i$ 是可學習的權重矩陣， $b^i$ 是偏置向量。

注意力門控g通過sigmoid激活函數生成，其值在0到1之間，控制信息流的強度：

$g = \sigma(W_q^g Q + W_v^g \hat{V} + b^g)$

最終的AoA輸出通過元素級乘法得到：

$\hat{i} = g \odot i$

這種設計的巧妙之處在于，當門控值接近0時，模型會抑制注意力信息的傳遞，有效地表達"無相關信息"的語義；當門控值接近1時，模型會充分利用注意力信息。這種自適應控制機制使得AoA網絡能夠根據輸入的質量和相關性動態調整注意力的強度。

4.3 AoA網絡的信息論解釋

從信息論的角度來看，AoA網絡實現了一種更加智能的信息選擇機制。傳統注意力機制可以看作是一種有損壓縮過程，它將輸入序列壓縮為固定長度的表示向量。然而，這種壓縮是"強制性"的，即使輸入信息質量很低，也會產生一個表示向量。AoA網絡通過引入門控機制，實現了"自適應壓縮"，當輸入信息質量不足時，可以選擇產生近似零向量的輸出。

這種機制可以用條件信息論來解釋。設Y表示AoA網絡的輸出，X表示輸入，R表示相關性變量，那么AoA網絡的目標可以表示為：

$\max I(Y; T|R) - \lambda I(Y; X|R=0)$

其中T表示目標任務， $I(\cdot; \cdot|\cdot)$ 表示條件互信息， $\lambda$ 是正則化參數。第一項鼓勵輸出與目標任務的相關性，第二項懲罰在無相關信息時的輸出復雜度。這種目標函數確保了AoA網絡在有相關信息時最大化信息傳遞，在無相關信息時最小化噪聲傳播。

4.4 AoA網絡在視頻水印中的應用機制

在視頻水印的應用場景中，AoA網絡被用于生成分數圖（Score Map），指導水印的嵌入位置選擇。視頻幀的不同區域具有不同的紋理復雜度、視覺顯著性和魯棒性特征，AoA網絡通過分析這些特征，生成一個分數圖來指示每個像素位置的嵌入適宜性。

具體而言，AoA網絡接收從深度信念網絡提取的視頻幀特征作為輸入，通過多頭注意力機制分析特征之間的相關性，然后通過門控機制生成最終的分數圖。這個過程可以數學化表示為：

$\text{ScoreMap}i = \text{AoA}(f{\text{att}}, Q_i, K_i, V_i)$

其中 $Q_i,K_i,V_i$ 分別表示第i個視頻幀的查詢、鍵、值表示， $f_{\text{att}}$ 表示注意力函數。

生成的分數圖具有重要的語義含義：高分數區域通常對應于紋理豐富、視覺不敏感且具有較強魯棒性的區域，這些區域適合嵌入水印信息；低分數區域則對應于平滑、視覺敏感或容易受攻擊影響的區域，應該避免在這些區域嵌入水印。這種自適應的位置選擇策略顯著提高了水印系統的整體性能，實現了不可感知性和魯棒性的良好平衡。

5. 深度信念網絡的理論基礎

5.1 概率圖模型與生成式建模

深度信念網絡（Deep Belief Network, DBN）是一種基于概率圖模型的深度生成模型，由Geoffrey Hinton在2006年提出。DBN的理論基礎建立在概率圖模型和無監督學習的交匯點上，它通過學習數據的概率分布來實現特征提取和數據生成的雙重功能。與傳統的判別式模型不同，生成式模型試圖學習數據的聯合概率分布P(X, Y)，其中X表示輸入數據，Y表示標簽。這種建模方式使得生成式模型不僅能夠進行分類預測，還能夠生成新的數據樣本。

DBN的概率建模基礎可以追溯到統計物理學中的玻爾茲曼分布。在這種框架下，系統的狀態由一個能量函數 $E(\mathbf{v}, \mathbf{h})$ 決定，其中 $\mathbf{v}$ 表示可見變量， $\mathbf{h}$ 表示隱變量。系統的概率分布遵循玻爾茲曼分布：

$P(\mathbf{v}, \mathbf{h}) = \frac{1}{Z} \exp(-E(\mathbf{v}, \mathbf{h}))$

其中Z是配分函數（Partition Function），用于歸一化概率分布：

$Z = \sum_{\mathbf{v}, \mathbf{h}} \exp(-E(\mathbf{v}, \mathbf{h}))$

這種概率建模方式的優勢在于能夠捕獲變量之間的復雜依賴關系，特別是高階相關性。在傳統的線性模型中，變量之間的關系通常假設為線性或簡單的非線性關系，而基于能量的模型能夠表示任意復雜的依賴結構。

5.2 受限玻爾茲曼機的數學原理

受限玻爾茲曼機（Restricted Boltzmann Machine, RBM）是DBN的基本構建單元。RBM是一種特殊的玻爾茲曼機，其"受限"特性體現在網絡結構的約束上：可見層內部沒有連接，隱藏層內部也沒有連接，只有可見層和隱藏層之間存在全連接。這種結構約束大大簡化了模型的訓練過程，使得條件概率的計算變得可行。

RBM的能量函數定義為：

$E(\mathbf{v}, \mathbf{h}) = -\mathbf{v}^T \mathbf{W} \mathbf{h} - \mathbf{a}^T \mathbf{v} - \mathbf{b}^T \mathbf{h}$

其中$\mathbf{W}$是連接權重矩陣，$\mathbf{a}$和$\mathbf{b}$分別是可見層和隱藏層的偏置向量。基于這個能量函數，可以推導出條件概率分布：

$P(h_j = 1|\mathbf{v}) = \sigma\left(\sum_i W_{ij} v_i + b_j\right)$$ $$P(v_i = 1|\mathbf{h}) = \sigma\left(\sum_j W_{ij} h_j + a_i\right)$

其中 $\sigma(x) = \frac{1}{1 + \exp(-x)}$ 是sigmoid激活函數。

這些條件概率公式揭示了RBM的重要特性：給定可見層的狀態，隱藏層單元的激活是相互獨立的；反之亦然。這種條件獨立性是RBM可訓練性的關鍵，它使得可以通過Gibbs采樣高效地從模型分布中采樣。

RBM的訓練目標是最大化觀測數據的對數似然：

$\mathcal{L} = \sum_{n=1}^{N} \log P(\mathbf{v}^{(n)})$

其中邊際概率 $P(\mathbf{v})$ 通過對隱變量求和得到：

$P(\mathbf{v}) = \sum_{\mathbf{h}} P(\mathbf{v}, \mathbf{h}) = \sum_{\mathbf{h}} \frac{1}{Z} \exp(-E(\mathbf{v}, \mathbf{h}))$

5.3 對比散度算法的理論基礎

RBM的直接最大似然訓練面臨著配分函數難以計算的問題，因為需要對所有可能的狀態組合求和。為了解決這個問題，Hinton提出了對比散度（Contrastive Divergence, CD）算法，這是一種近似的梯度估計方法。

對比散度算法的核心思想是用短鏈Gibbs采樣來近似模型分布下的期望。標準的梯度計算需要計算數據分布和模型分布下的期望差：

$\frac{\partial \mathcal{L}}{\partial \theta} = \mathbb{E}{\text{data}}[\frac{\partial E}{\partial \theta}] - \mathbb{E}{\text{model}}[\frac{\partial E}{\partial \theta}]$

其中第一項可以直接從訓練數據計算，第二項需要從模型分布采樣。對比散度算法用$k$步Gibbs采樣來近似模型分布下的期望：

從訓練樣本 $\mathbf{v}^{(0)}$ 開始
計算 $P(\mathbf{h}^{(0)}|\mathbf{v}^{(0)})$ 并采樣 $\mathbf{h}^{(0)}$
計算 $P(\mathbf{v}^{(1)}|\mathbf{h}^{(0)})$ 并采樣 $\mathbf{v}^{(1)}$
重復k次得到 $\mathbf{v}^{(k)}$

對比散度的梯度估計為：

$\frac{\partial \mathcal{L}{\text{CD}}}{\partial \theta} = \mathbb{E}{\text{data}}[\frac{\partial E}{\partial \theta}] - \mathbb{E}_{\mathbf{v}^{(k)}}[\frac{\partial E}{\partial \theta}]$

理論分析表明，當 $k \to \infty$ 時，CD算法收斂到真實的最大似然梯度。在實踐中，即使k=1（CD-1），算法也能獲得良好的性能。這種近似的理論基礎在于Gibbs采樣的快速混合性質：在大多數實際數據分布下，短鏈采樣已經能夠捕獲模型分布的主要特征。

5.4 DBN的逐層貪心訓練策略

DBN通過逐層貪心訓練策略解決了深層網絡的訓練難題。這種策略的理論依據來自于復合函數的近似理論和信息瓶頸原理。每一層RBM可以看作是對輸入數據的一種信息壓縮和特征提取，而多層的堆疊則實現了層次化的特征學習。

DBN的訓練過程可以分為兩個階段：無監督預訓練和有監督微調。在預訓練階段，從底層開始，逐層訓練每個RBM：

訓練第一層RBM： ${W^{(1)}, \mathbf{a}^{(1)}, \mathbf{b}^{(1)}} = \arg\max_{\theta} \sum_n \log P(\mathbf{v}_n; \theta)$
固定第一層參數，用 $P(\mathbf{h}^{(1)}|\mathbf{v})$ 的期望作為第二層的輸入
訓練第二層RBM： ${W^{(2)}, \mathbf{b}^{(1)}, \mathbf{b}^{(2)}} = \arg\max_{\theta} \sum_n \log P(\mathbf{h}_n^{(1)}; \theta)$
重復直到所有層訓練完成

這種逐層訓練策略的理論優勢在于每一層的訓練都有明確的目標函數，避免了深層網絡訓練中的梯度消失和局部最優問題。更重要的是，每一層都學習到了前一層表示的更抽象的特征，實現了從低級特征到高級特征的層次化學習。

數學上，DBN的完整概率模型可以表示為：

$P(\mathbf{v}, \mathbf{h}^{(1)}, ..., \mathbf{h}^{(L)}) = P(\mathbf{v}|\mathbf{h}^{(1)}) \prod_{l=1}^{L-1} P(\mathbf{h}^{(l)}|\mathbf{h}^{(l+1)}) P(\mathbf{h}^{(L-1)}, \mathbf{h}^{(L)})$

其中底層是有向的信念網絡，頂層是無向的RBM。這種混合的圖結構既保留了生成模型的優勢，又具有了判別模型的表達能力。

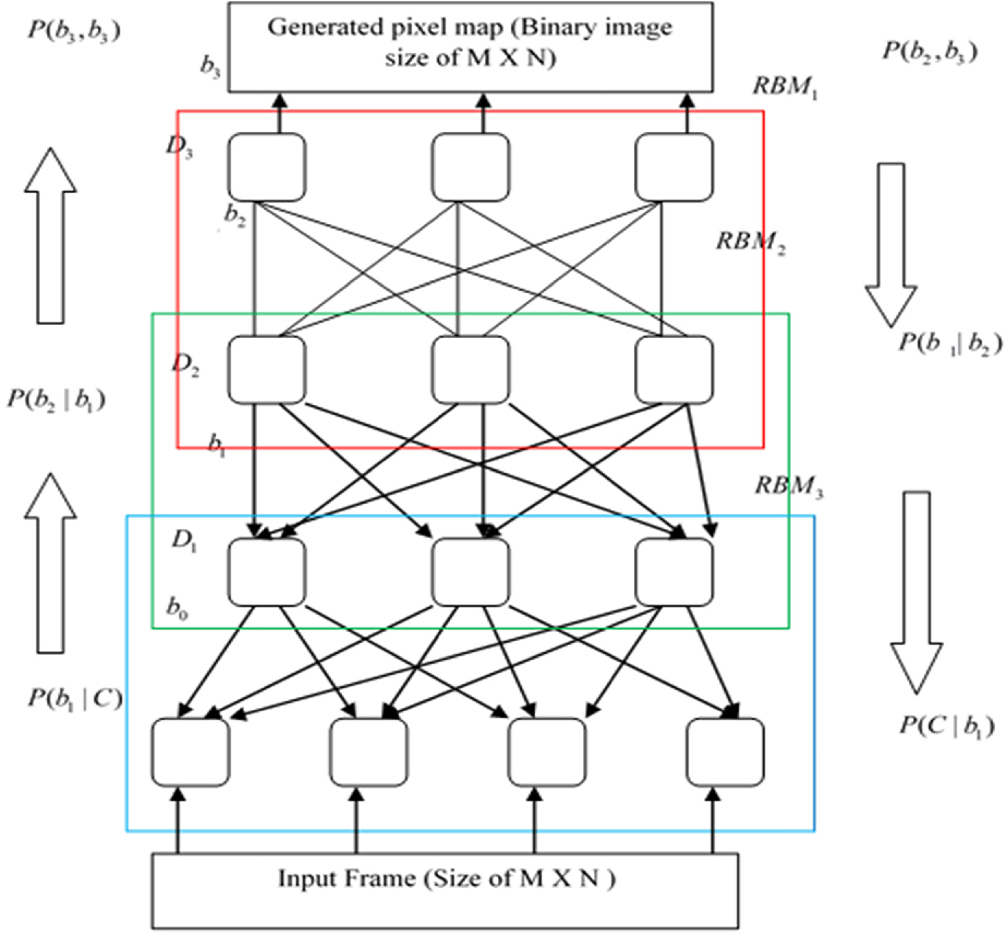
6. 四元數曲波變換的數學原理

6.1 四元數代數的基礎理論

四元數（Quaternion）是由愛爾蘭數學家Hamilton在1843年發明的一種擴展的數系統，它是復數在高維空間的推廣。四元數在計算機圖形學、機器人學和信號處理等領域有著廣泛的應用，特別是在表示三維旋轉和處理彩色圖像時展現出獨特的優勢。一個四元數可以表示為：

$q = q_0 + q_1 i + q_2 j + q_3 k$

其中 $q_0, q_1, q_2, q_3 \in \mathbb{R},i, j, k$ 是四元數的基本單位，滿足以下乘法規則：

$i^2 = j^2 = k^2 = ijk = -1$$ $$ij = k, \quad jk = i, \quad ki = j$$ $$ji = -k, \quad kj = -i, \quad ik = -j$

這些乘法規則定義了四元數的非交換代數結構，這種非交換性使得四元數能夠表示三維空間中的旋轉操作。

在信號處理中，四元數的一個重要應用是表示彩色圖像。傳統的彩色圖像處理方法通常將RGB三個通道分別處理，忽略了通道之間的相關性。而四元數表示法可以將彩色圖像編碼為一個四元數信號：

$f(x, y) = f_R(x, y) i + f_G(x, y) j + f_B(x, y) k$

其中 $f_R, f_G, f_B$ 分別表示紅、綠、藍三個顏色通道。這種表示方法的優勢在于能夠同時處理三個顏色通道，保持通道間的相關性，從而獲得更好的處理效果。

四元數的模長定義為：

$|q| = \sqrt{q_0^2 + q_1^2 + q_2^2 + q_3^2}$

四元數的共軛定義為：

$\bar{q} = q_0 - q_1 i - q_2 j - q_3 k$

四元數的逆定義為：

$q^{-1} = \frac{\bar{q}}{|q|^2}$

6.2 四元數傅里葉變換的理論基礎

四元數傅里葉變換（Quaternion Fourier Transform, QFT）是傅里葉變換在四元數域的推廣，它能夠同時分析信號在多個維度上的頻域特性。二維QFT的定義為：

$\mathcal{F}q[f](u, v) = \int{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, y) e^{-\mu 2\pi(ux + vy)} dx dy$

其中 $\mu$ 是一個單位純四元數，通常選擇為 $\mu = \frac{i + j + k}{\sqrt{3}}$ 。這個選擇確保了變換的對稱性和旋轉不變性。

QFT的一個重要特性是它能夠將信號分解為不同方向和頻率的分量。與傳統的復數傅里葉變換相比，QFT提供了更豐富的頻域表示，能夠更好地分析彩色圖像和多通道信號的特性。QFT的逆變換定義為：

$f(x, y) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \mathcal{F}_q[f](u, v) e^{\mu 2\pi(ux + vy)} du dv$

QFT具有線性性、平移性、旋轉協變性等重要性質。特別地，QFT的旋轉協變性表明，當輸入信號發生旋轉時，其QFT也會發生相應的旋轉，這種性質在處理幾何變換時非常有用。

6.3 曲波變換的多尺度幾何分析

曲波變換（Curvelet Transform）是一種新興的多尺度幾何分析工具，由Candès和Donoho在21世紀初提出。與傳統的小波變換相比，曲波變換在處理具有方向性特征的信號時具有顯著優勢，特別是在圖像中的邊緣和線性特征分析方面。

曲波變換的基本思想是構造一族具有方向選擇性的基函數，這些基函數在不同尺度上具有不同的長寬比。在粗尺度上，曲波基函數接近于各向同性的；在細尺度上，曲波基函數變得高度各向異性，呈現出細長的形狀。這種設計使得曲波能夠稀疏地表示具有線性和曲線特征的信號。

連續曲波的定義基于極坐標系。在頻域中，曲波的支撐集由尺度參數a和角度參數 $\theta$ 確定：

$\text{supp}(\hat{\psi}_{a,\theta}) \subset {(\rho, \phi) : \rho \sim 2^{-j}, |\phi - \theta| \lesssim 2^{-j/2}}$

其中j是尺度指標， $\rho$ 和 $\phi$ 分別表示極徑和極角。這個支撐集的形狀類似于楔形，其寬度隨著尺度的減小而減小，體現了曲波的方向選擇性。

離散曲波變換通過在頻域中的楔形分割來實現。具體步驟包括：

對輸入信號進行2D FFT
在頻域中應用角度和徑向窗函數
對每個楔形區域進行逆FFT
應用適當的重采樣和包裝操作

曲波變換的一個重要理論結果是其在表示分片光滑圖像時的最優稀疏性。對于包含$C^2$曲線的分片$C^2$圖像，曲波變換能夠實現接近最優的非線性逼近誤差。

6.4 四元數曲波變換的構造與性質

四元數曲波變換（Quaternion Curvelet Transform, QCT）是曲波變換在四元數域的推廣，它結合了四元數代數的優勢和曲波變換的幾何分析能力。QCT的構造基于四元數傅里葉變換和曲波分析的結合。

QCT的實現過程可以描述如下：

將輸入的彩色圖像表示為四元數信號： $f_q(x, y) = f_R(x, y) i + f_G(x, y) j + f_B(x, y) k$
計算四元數傅里葉變換： $\hat{f}_q(u, v) = \mathcal{F}_q[f_q](u, v)$
在四元數頻域中應用曲波分析： $C_{j,l,k} = \langle \hat{f}q, \hat{\psi}{j,l,k} \rangle$

其中j, l, k分別表示尺度、方向和位置參數， $\hat{\psi}_{j,l,k}$ 是四元數曲波基函數。

QCT具有以下重要性質：

完美重構性：存在對偶基函數使得原始信號可以完美重構： $f_q = \sum_{j,l,k} C_{j,l,k} \psi_{j,l,k}$

旋轉協變性：當輸入信號發生旋轉時，QCT系數也會發生相應的變化，保持幾何結構的一致性。

顏色不變性：QCT能夠捕獲圖像的幾何結構信息，對顏色空間的線性變換具有一定的魯棒性。

稀疏表示：對于具有方向性特征的彩色圖像，QCT能夠提供稀疏的表示，大部分能量集中在少數幾個重要系數上。

在水印應用中，QCT的優勢主要體現在：

多通道處理：能夠同時處理RGB三個顏色通道，保持通道間的相關性
方向選擇性：能夠精確定位圖像中的邊緣和紋理方向
多尺度分析：在不同尺度上提供不同的頻率分辨率
幾何不變性：對常見的幾何變換具有一定的魯棒性

這些特性使得QCT成為視頻水印應用中理想的變換域選擇。

7. Golden Section Fibonacci Tree Optimization算法

7.1 黃金分割的數學美學與優化原理

黃金分割（Golden Section）是數學中一個具有深刻美學意義的概念，其比值 $\phi = \frac{1 + \sqrt{5}}{2} \approx 1.618$ 在自然界和藝術中廣泛存在。從數學角度來看，黃金分割具有獨特的自相似性質： $\phi^2 = \phi + 1$ ，這種性質使得黃金分割在優化算法中具有特殊的價值。黃金分割搜索算法是一種基于單峰函數假設的單變量優化方法，它通過逐步縮小搜索區間來逼近最優解。

黃金分割搜索的基本原理是在每次迭代中，將搜索區間按黃金分割比例分為兩部分，通過比較分割點處的函數值來決定下一步的搜索方向。設搜索區間為 $[a, b]$ ，兩個內部分割點為：

$x_1 = a + (1 - \frac{1}{\phi})(b - a) = a + 0.382(b - a)$$ $$x_2 = a + \frac{1}{\phi}(b - a) = a + 0.618(b - a)$

通過比較 $f(x_1)$ 和 $f(x_2)$ 的大小，可以排除區間的一部分，新的搜索區間長度為原來的 $\frac{1}{\phi} \approx 0.618$ 倍。這種方法的收斂速度是線性的，收斂常數為 $\frac{1}{\phi}$ ，在單變量優化中具有良好的理論性質。

黃金分割搜索的一個重要優勢是其魯棒性。算法不需要計算函數的導數信息，只需要進行函數值比較，因此適用于非光滑、非凸甚至不連續的目標函數。在實際應用中，黃金分割搜索經常作為其他優化算法的組件，用于線搜索或區間縮放。

7.2 斐波那契數列的遞歸結構與優化應用

斐波那契數列是數學中最著名的遞歸序列之一，定義為： $F_0 = 0, F_1 = 1, F_n = F_{n-1} + F_{n-2}$ 。斐波那契數列與黃金分割有著密切的聯系：當 $n \to \infty$ 時，相鄰斐波那契數的比值趨向于黃金分割比：

$\lim_{n \to \infty} \frac{F_{n+1}}{F_n} = \phi$

這種聯系使得斐波那契數列在優化算法中具有重要應用。斐波那契搜索算法是黃金分割搜索的一個變種，它使用斐波那契數來確定搜索區間的分割點。與黃金分割搜索相比，斐波那契搜索在有限步數內具有更好的收斂性質。

斐波那契樹優化（Fibonacci Tree Optimization, FTO）算法是一種基于斐波那契數列的群體智能優化算法。該算法模擬了斐波那契數列的生長模式，將搜索空間組織成樹狀結構，每個節點代表一個候選解。算法的核心思想是通過模擬斐波那契數列的遞歸關系來生成新的候選解：

$x_n = x_{n-1} + x_{n-2} + \epsilon$

其中 $\epsilon$ 是隨機擾動項，用于維持種群的多樣性。

FTO算法的樹狀結構使得算法能夠在全局搜索和局部搜索之間取得良好的平衡。樹的根節點對應于全局最優解的估計，葉節點對應于局部搜索的候選解。通過控制樹的深度和分支因子，可以調節算法在探索（exploration）和利用（exploitation）之間的權衡。

7.3 GSFTO算法的設計理念與數學模型

Golden Section Fibonacci Tree Optimization（GSFTO）算法是黃金分割搜索和斐波那契樹優化的有機結合，旨在繼承兩種方法的優勢。GSFTO算法的設計理念是將黃金分割的精確性與斐波那契數列的遞歸結構相結合，構造一種既具有良好收斂性又能維持種群多樣性的優化算法。

GSFTO算法的數學模型包含以下幾個關鍵組件：

種群初始化：算法首先在搜索空間中隨機初始化$N$個個體，每個個體的位置向量表示為：

$\mathbf{x}i = \mathbf{x}{\min} + \text{rand}(0,1) \cdot (\mathbf{x}{\max} - \mathbf{x}{\min})$

其中 $\mathbf{x}{\min},\mathbf{x}{\max}$ 分別表示搜索空間的下界和上界。

黃金分割更新策略：在每次迭代中，算法使用黃金分割原理來更新個體位置。對于第$i$個個體，其更新公式為：

$\mathbf{x}i^{(t+1)} = \mathbf{x}{\text{best}}^{(t)} + \phi^{-1} \cdot (\mathbf{x}i^{(t)} - \mathbf{x}{\text{best}}^{(t)}) + \mathbf{r}$

其中 $\mathbf{x}_{\text{best}}^{(t)}$ 表示當前最優解， $\mathbf{r}$ 是隨機向量，用于維持種群多樣性。

斐波那契遞歸機制：算法引入斐波那契遞歸機制來生成新的候選解：

$\mathbf{x}{\text{new}} = \alpha \mathbf{x}{F_{n-1}} + \beta \mathbf{x}{F{n-2}} + \gamma \mathbf{x}_{\text{random}}$

其中 $\alpha, \beta, \gamma$ 是權重系數，滿足 $\alpha + \beta + \gamma = 1,\mathbf{x}{F{n-1}},\mathbf{x}{F{n-2}}$ 分別表示按斐波那契指標排序的候選解。

適應性參數調節：GSFTO算法采用自適應參數調節機制，根據算法的收斂狀態動態調整搜索參數：

$\alpha(t) = \alpha_0 \cdot \exp\left(-\frac{t}{T}\right)$

其中 $\alpha_0$ 是初始參數值，T是最大迭代次數，這種指數衰減策略確保算法從全局搜索逐漸轉向局部搜索。

7.4 GSFTO在深度網絡優化中的應用

在深度信念網絡的訓練過程中，GSFTO算法被用于優化網絡的權重和偏置參數。傳統的梯度下降方法在訓練DBN時容易陷入局部最優，而且對初始化敏感。GSFTO算法通過其全局搜索能力，能夠為DBN提供更好的參數初始化，從而提高網絡的訓練效果。

GSFTO在DBN優化中的應用可以形式化為以下優化問題：

$\min_{\Theta} \mathcal{L}(\Theta) = \min_{\Theta} \left[-\sum_{i=1}^{N} \log P(\mathbf{v}_i | \Theta)\right]$

其中 $\Theta = {W, \mathbf{a}, \mathbf{b}}$ 表示DBN的所有參數， $\mathcal{L}(\Theta)$ 是負對數似然損失函數。

GSFTO算法的適應度函數設計為：

$f(\Theta) = \frac{1}{N} \sum_{i=1}^{N} (y_i^* - y_i(\Theta))^2 + \lambda |\Theta|_2^2$

其中第一項是重構誤差，第二項是正則化項， $\lambda$ 是正則化系數。

算法的具體執行步驟包括：

種群初始化：隨機生成$M$個參數向量組成初始種群
適應度評估：計算每個個體的適應度值
黃金分割更新：使用黃金分割策略更新個體位置
斐波那契重組：應用斐波那契遞歸關系生成新個體
選擇操作：根據適應度值選擇下一代種群
收斂判斷：檢查終止條件，若滿足則停止，否則返回步驟2

這種優化策略的優勢在于能夠有效平衡全局搜索和局部搜索，避免傳統梯度方法的局部最優問題，為DBN提供高質量的參數初始化。

8. 技術融合與系統架構

8.1 多技術融合的理論基礎

在現代機器學習和信號處理系統中，單一技術往往難以解決復雜的實際問題，多技術融合已成為提升系統性能的重要手段。技術融合的理論基礎可以從信息論、優化理論和系統論的角度來理解。從信息論的視角，不同技術往往捕獲數據的不同方面的信息，通過融合可以獲得更完整的信息描述。從優化理論的角度，多技術融合相當于在更大的假設空間中尋找最優解，理論上能夠獲得更好的性能。從系統論的視角，技術融合體現了系統的整體性原理，即整體的功能大于各部分功能的簡單疊加。

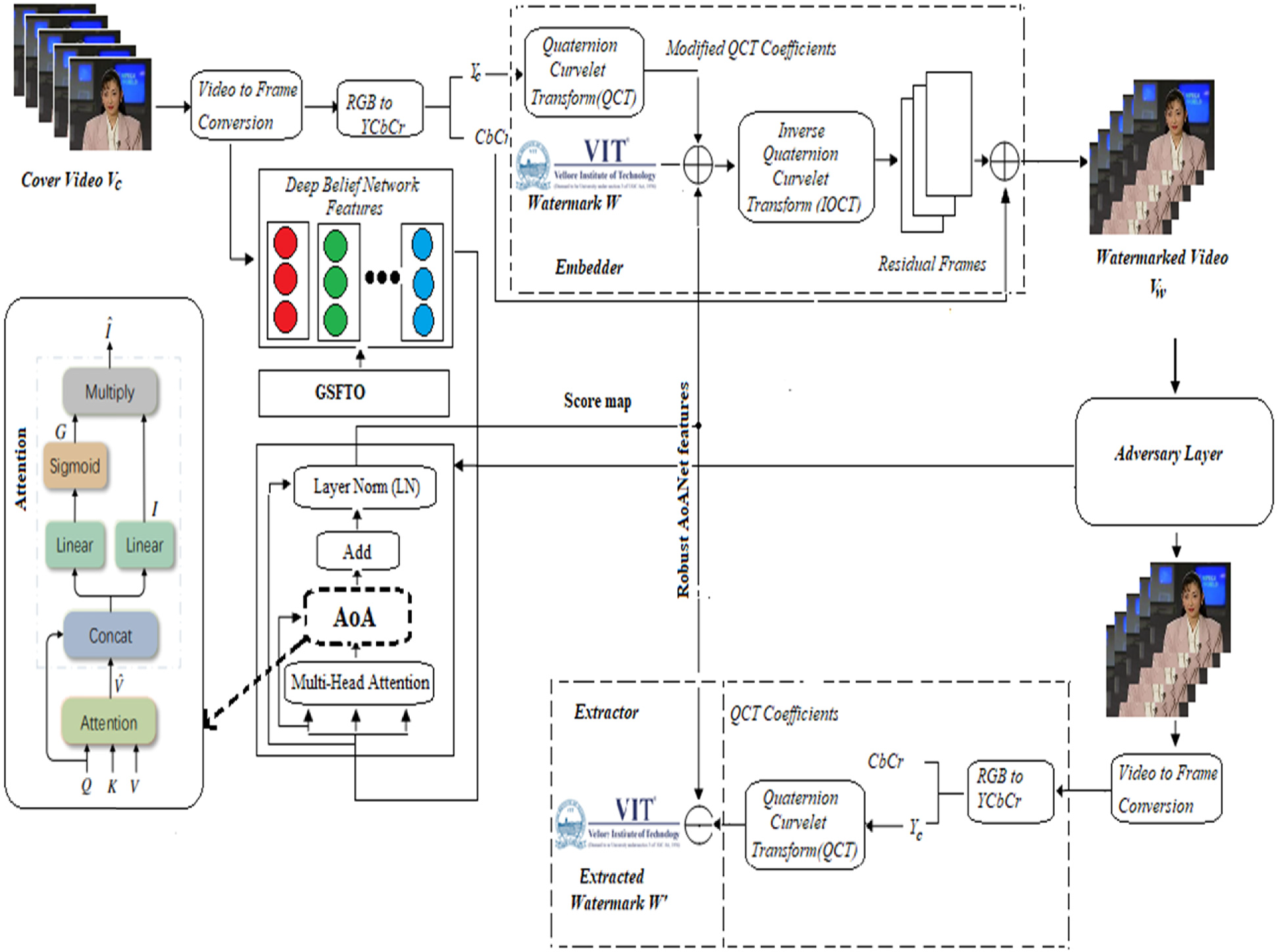
在本論文的技術架構中，AoA網絡、DBN、QCT和GSFTO四種技術的融合體現了深度學習、傳統信號處理和智能優化的有機結合。這種融合不是簡單的技術疊加，而是基于各技術特點的協同設計。AoA網絡負責智能的注意力分配，DBN提供強大的特征提取能力，QCT實現高效的頻域分析，GSFTO保證參數優化的全局性。

技術融合的數學模型可以表示為一個復合函數：

$y = h(g(f_1(x), f_2(x)), f_3(x), f_4(x))$

其中 $f_1, f_2, f_3, f_4$ 分別表示四種核心技術的映射函數，g表示中間層的融合函數，h表示最終的輸出函數。這種層次化的融合結構使得不同技術能夠在不同層次上發揮作用，實現功能的互補和增強。

8.2 系統架構的設計原則

視頻水印系統的架構設計需要遵循幾個重要原則。首先是模塊化原則，即將復雜系統分解為相對獨立的功能模塊，每個模塊負責特定的功能，模塊間通過明確的接口進行通信。這種設計有利于系統的開發、測試和維護，也便于對單個模塊進行優化和替換。其次是層次化原則，即將系統功能按照抽象層次進行組織，低層提供基礎功能，高層實現復雜邏輯。這種設計使得系統具有良好的可擴展性和可維護性。

在本論文的系統架構中，整個水印系統可以分為四個主要層次：預處理層、特征提取層、水印處理層和后處理層。預處理層負責視頻的格式轉換、關鍵幀提取等基礎功能；特征提取層使用DBN和AoA網絡提取視頻的深層特征；水印處理層在QCT域中進行水印嵌入和提取；后處理層負責視頻的重構和質量評估。

系統的數據流可以用以下流程圖描述：

8.3 關鍵幀提取與二進制像素圖生成

關鍵幀提取是視頻水印系統的重要組成部分，它直接影響水印的嵌入效率和系統性能。有效的關鍵幀提取策略應該能夠選擇出視覺上重要、信息量豐富且具有較強魯棒性的幀。本系統采用基于內容復雜度和運動信息的關鍵幀提取方法。

關鍵幀的重要性評分可以通過以下公式計算：

$\text{Score}(f_i) = \alpha \cdot \text{Complexity}(f_i) + \beta \cdot \text{Motion}(f_i) + \gamma \cdot \text{Texture}(f_i)$

其中 $\text{Complexity}(f_i)$ 表示第i幀的復雜度， $\text{Motion}(f_i)$ 表示運動信息， $\text{Texture}(f_i)$ 表示紋理豐富度， $\alpha, \beta, \gamma$ 是權重系數。

復雜度可以通過圖像的梯度信息來衡量：

$\text{Complexity}(f_i) = \frac{1}{MN} \sum_{x=1}^{M} \sum_{y=1}^{N} \sqrt{(\nabla_x f_i(x,y))^2 + (\nabla_y f_i(x,y))^2}$

運動信息可以通過相鄰幀間的光流場來估計：

$\text{Motion}(f_i) = \frac{1}{MN} \sum_{x=1}^{M} \sum_{y=1}^{N} \sqrt{u_i(x,y)^2 + v_i(x,y)^2}$

其中 $u_i(x,y),v_i(x,y)$ 分別表示位置 $(x,y)$ 處的水平和垂直光流分量。

二進制像素圖的生成是基于深度信念網絡的特征分析結果。DBN通過無監督學習提取視頻幀的深層特征表示，這些特征包含了像素級的重要性信息。二進制像素圖的生成過程可以表示為：

$\text{BinaryMap}(x,y) = \begin{cases} 1, & \text{if } \text{Importance}(x,y) > \tau, \\ 0, & \text{otherwise}. \end{cases}$

其中 $\text{Importance}(x,y)$ 表示位置 $(x,y)$ 的重要性得分， $\tau$ 是閾值參數。

8.4 水印嵌入與提取的數學模型

水印嵌入過程是整個系統的核心，它需要在保證視覺質量的前提下，將水印信息魯棒地嵌入到視頻中。本系統在QCT域中進行水印嵌入，嵌入公式為：

$C_w(u,v) = C(u,v) + \alpha \cdot S(u,v) \cdot W(u,v)$

其中 $C(u,v)$ 表示原始QCT系數， $W(u,v)$ 表示水印信號， $S(u,v)$ 表示AoA網絡生成的分數圖， $\alpha$ 表示嵌入強度， $C_w(u,v)$ 表示嵌入水印后的QCT系數。

分數圖$S(u,v)$的作用是提供自適應的嵌入強度控制。在紋理豐富、視覺不敏感的區域，分數圖的值較大，允許更強的水印嵌入；在平滑、視覺敏感的區域，分數圖的值較小，限制水印的嵌入強度。這種自適應機制確保了水印在提供魯棒性的同時保持良好的視覺質量。

水印提取過程是嵌入過程的逆操作：

$W'(u,v) = \frac{C'_w(u,v) - C(u,v)}{\alpha \cdot S(u,v)}$

其中 $C'_w(u,v)$ 表示從可能受到攻擊的視頻中提取的QCT系數， $W'(u,v)$ 表示提取的水印信號。

為了提高提取的精度，系統還采用了統計檢測方法。對于二值水印，可以使用相關檢測器：

$\rho = \frac{\sum_{u,v} W(u,v) \cdot W'(u,v)}{\sqrt{\sum_{u,v} W(u,v)^2} \sqrt{\sum_{u,v} W'(u,v)^2}}$

當 $\rho$ 超過預設閾值時，判斷水印存在；否則判斷水印不存在或已被破壞。

這種基于多技術融合的水印系統架構，通過各技術模塊的協同工作，實現了在復雜攻擊環境下的魯棒水印嵌入和提取，為視頻版權保護提供了有效的技術解決方案。

9. 總結與展望

9.1 技術創新點總結

本文深入解析了基于混合注意力網絡和深度信念網絡的魯棒視頻水印技術的基礎理論，涵蓋了數字水印技術、注意力機制、深度信念網絡、四元數曲波變換以及優化算法等多個重要領域的核心概念。通過對這些基礎理論的系統性闡述，我們可以清晰地看到現代視頻水印技術的理論根基和發展脈絡。

論文《DeepSecure watermarking: Hybrid Attention on Attention Net and Deep Belief Net based robust video authentication using Quaternion Curvelet Transform domain》的主要技術創新體現在多個層面。首先，在注意力機制的應用方面，該研究首次將Attention on Attention網絡引入視頻水印領域，通過門控機制實現了對注意力信息的智能控制，有效解決了傳統注意力機制的"盲目性"問題。其次，在特征提取方面，研究采用深度信念網絡提取視頻幀的深層特征表示，并結合GSFTO優化算法進行參數優化，顯著提升了特征提取的質量和效率。第三，在變換域選擇方面，四元數曲波變換的應用實現了對彩色視頻多通道信息的統一處理，保持了通道間的相關性，提高了水印的魯棒性。最后，在系統架構方面，多技術融合的設計理念實現了不同技術優勢的互補，構建了一個性能優異的視頻水印系統。

9.2 理論意義與實際價值

從理論意義來看，這項研究代表了視頻水印技術從傳統信號處理向深度學習范式的重要轉變。傳統的水印方法主要依賴于手工設計的特征和啟發式的嵌入策略，而基于深度學習的方法能夠自動學習最優的特征表示和嵌入策略。特別是注意力機制的引入，使得水印系統具備了類似人類視覺注意力的智能選擇能力，能夠自適應地關注最重要的視頻內容區域。這種從"被動嵌入"到"主動選擇"的轉變，體現了人工智能技術在傳統信號處理領域的深度融合和創新應用。

深度信念網絡作為深度學習的重要先驅技術，在視頻水印中的成功應用證明了生成式模型在特征學習方面的獨特優勢。與判別式模型相比，生成式模型能夠學習數據的內在分布特征，這對于理解視頻內容的語義結構具有重要價值。四元數曲波變換的應用則體現了多維信號處理理論的發展，它不僅能夠處理傳統的空域和頻域信息，還能夠有效分析顏色空間的相關性和幾何結構的方向性。

從實際應用價值來看，這項研究為解決當前視頻版權保護面臨的挑戰提供了新的技術路徑。隨著高清視頻、4K視頻甚至8K視頻的普及，傳統的水印技術在處理大容量、高分辨率視頻時面臨著計算效率和存儲空間的雙重壓力。基于深度學習的水印方法通過智能的關鍵幀選擇和自適應的嵌入策略，能夠在保證水印質量的前提下顯著降低計算復雜度。此外，系統對各種攻擊的強魯棒性使其能夠應對復雜的網絡傳輸環境和多樣化的惡意攻擊，為實際的商業應用提供了可靠的技術保障。

9.3 技術發展趨勢與挑戰

當前，視頻水印技術正朝著更加智能化、自適應化的方向發展。人工智能技術的快速進步為水印領域帶來了新的機遇，同時也提出了新的挑戰。從技術發展趨勢來看，未來的視頻水印技術可能會更加注重以下幾個方面：

在算法層面，端到端的深度學習框架將成為主流。傳統的水印系統通常由多個相對獨立的模塊組成，模塊間的接口設計和參數調優往往需要大量的人工干預。而端到端的深度學習框架能夠將整個水印流程統一在一個可微分的網絡中，通過梯度下降算法實現全局優化。這種方法不僅能夠簡化系統設計，還能夠獲得更好的整體性能。

在計算效率方面，輕量化網絡設計將成為重要研究方向。隨著移動設備和邊緣計算的普及，水印算法需要能夠在資源受限的環境中高效運行。這要求研究者在保證算法性能的前提下，盡可能減少模型參數和計算復雜度。知識蒸餾、網絡剪枝、量化等技術將在水印領域得到更廣泛的應用。

在魯棒性方面，對抗性訓練和元學習技術的應用將進一步提升水印的抗攻擊能力。傳統的魯棒性測試通常基于已知的攻擊類型，而實際應用中可能面臨未知的攻擊方式。通過對抗性訓練，水印系統能夠學習到更加泛化的抗攻擊特征；通過元學習，系統能夠快速適應新的攻擊類型。

然而，技術發展也面臨著諸多挑戰。首先是安全性挑戰，隨著深度學習技術的普及，基于神經網絡的攻擊方法也在不斷發展。對抗樣本攻擊、模型逆向工程等技術可能對基于深度學習的水印系統構成威脅。其次是標準化挑戰，目前的深度學習水印方法往往缺乏統一的評估標準和性能基準，這限制了不同方法之間的公平比較和技術進步。最后是可解釋性挑戰，深度學習模型的"黑箱"特性使得水印系統的決策過程難以理解和解釋，這在某些應用場景中可能成為技術采用的障礙。

9.4 未來研究方向

基于當前的技術發展狀況和面臨的挑戰，未來的視頻水印研究可能會在以下幾個方向取得突破：

多模態水印技術將成為重要的研究方向。現代的多媒體內容往往包含視頻、音頻、文本等多種模態信息，單一模態的水印可能無法提供足夠的安全保障。多模態水印技術通過在不同模態中協同嵌入水印信息，不僅能夠提高水印的容量和魯棒性，還能夠實現跨模態的版權保護。這種技術的實現需要深入研究不同模態之間的相關性和互補性，設計有效的多模態融合策略。

區塊鏈與水印技術的結合將為數字版權保護提供新的解決方案。區塊鏈技術的去中心化、不可篡改等特性與水印技術的隱蔽性、魯棒性形成良好的互補。通過將水印信息的哈希值記錄在區塊鏈上，可以實現水印的時間戳認證和不可否認性。同時，智能合約技術可以自動化水印的驗證和版權確認過程，降低版權保護的成本和復雜度。

隱私保護水印將成為重要的研究方向。隨著隱私保護意識的增強和相關法規的完善，傳統的水印技術可能面臨隱私泄露的風險。差分隱私、同態加密等隱私保護技術與水印技術的結合，能夠在保護內容版權的同時保護用戶隱私。這種技術的發展需要在版權保護強度、隱私保護程度和系統性能之間找到合適的平衡點。

關于實驗驗證部分，由于篇幅限制，本文主要聚焦于基礎理論的深度解析。該論文的詳細實驗結果、性能評估和比較分析可以參考原始論文《DeepSecure watermarking: Hybrid Attention on Attention Net and Deep Belief Net based robust video authentication using Quaternion Curvelet Transform domain》，其中包含了在多個標準數據集上的全面實驗驗證，以及與現有先進方法的詳細性能比較。

通過對這些基礎理論的深入理解，我們可以更好地把握視頻水印技術的發展脈絡和未來趨勢，為相關研究和應用提供理論指導和技術支撐。隨著人工智能技術的不斷發展，相信視頻水印技術將在保護數字內容版權、維護網絡信息安全方面發揮越來越重要的作用。