《數學模型》經典案例——鋼管的訂購與運輸

一、問題描述

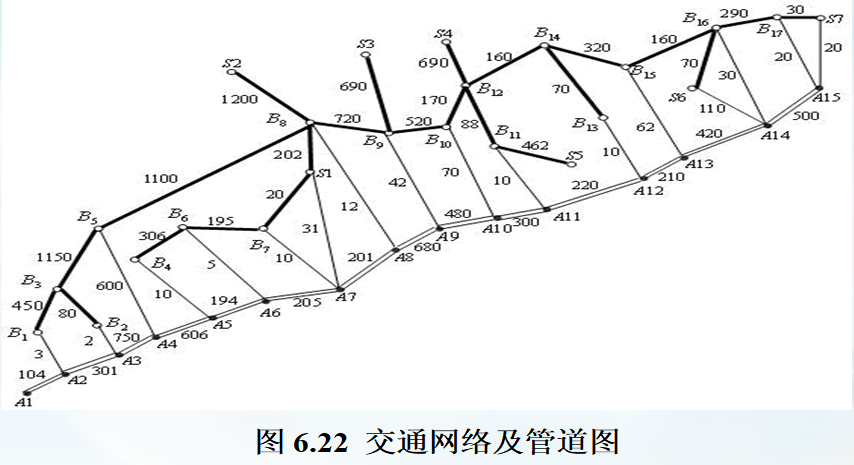
要鋪設一條 $A1→A2→?→A15A_1 \rightarrow A_2 \rightarrow \cdots \rightarrow A_{15}$ 的輸送天然氣的主管道，如圖 6.22 所示。經篩選后可以生產這種主管道鋼管的鋼廠有 $S1,S2,?,S7S_1, S_2, \cdots, S_7$ 。圖中粗線表示鐵路，單細線表示公路，雙細線表示要鋪設的管道（假設沿管道或者原來有公路，或者建有施工公路），圓圈表示火車站，每段鐵路、公路和管道旁的阿拉伯數字表示里程（單位 km）。
在這里插入圖片描述
為方便計，1km 主管道鋼管稱為 1 單位鋼管。

一個鋼廠如果承擔制造這種鋼管，至少需要生產 500 個單位。鋼廠 $S_i$ 在指定期限內能生產該鋼管的最大數量為 $s_i$ 個單位，鋼管出廠銷價 1 單位鋼管為 $p_i$ 萬元，見表 6.9；1 單位鋼管的鐵路運價見表 6.10。

							表 6.9 各鋼管廠的供貨上限及銷價

i	1	2	3	4	5	6	7
$s_i$	800	800	1000	2000	2000	2000	3000
$p_i$	160	155	155	160	155	150	160

							表 6.10 單位鋼管的鐵路運價

里程(km)	≤300	301~350	351~400	401~450	451~500
運價(萬元)	20	23	26	29	32
里程(km)	501~600	601~700	701~800	801~900	901~1000
運價(萬元)	37	44	50	55	60

1000km 以上每增加 1 至 100km 運價增加 5 萬元。公路運輸費用為 1 單位鋼管每公里 0.1 萬元（不足整公里部分按整公里計算）。鋼管可由鐵路、公路運往鋪設地點（不只是運到點 $A1,A2,?,A15A_1, A_2, \cdots, A_{15}$ ，而是管道全線）請制定一個主管道鋼管的訂購和運輸計劃，使總費用最小（給出總費用）。

二、問題分析

問題的建模目的是求一個主管道鋼管的訂購和運輸策略，使總費用最小。首先，問題給出了 7 個供選擇的鋼廠，選擇哪些？訂購多少？是一個要解決的問題。其次，每一個鋼廠到鋪設地點大多都有多條可供選擇的運輸路線，應選擇哪一條路線運輸，取決于建模的目標。而目標總費用包含兩個組成部分：訂購費用和運輸費用。訂購費用取決于單價和訂購數量，運輸費用取決于往哪里運和運輸路線。結合總目標的要求，可以很容易地想到應選擇運費最小的路線。
從同一個鋼管廠訂購鋼管運往同一個目的地，一旦最小運輸費用路線確定，則單位鋼管的運費就確定了，單位鋼管的訂購及運輸費用=鋼管單價+運輸費用。因此，同一個鋼管廠訂購鋼管運往同一個目的地的總費用等于訂購數量乘以單位鋼管的購運費用（單價+單位鋼管運費）。因而，在制定訂購與運輸計劃時，要分成兩個子問題考慮：

(1)運輸路線及運輸費用的確定：鋼管可以通過鐵路或公路運輸，公路運費是運輸里程的線性函數，但是鐵路運價卻是一種分段的階躍的常數函數。因此在計算時，不管對運輸里程還是費用而言，都不具有可加性，只能將鐵路運價（即由運輸總里程找出對應費率）和公路運價分別計算后再疊加。

(2)鋪設方案的設定：從鋼管廠訂購若干個單位的鋼管運送至樞紐點 $A1,A2,?,A15A_{1}, A_{2}, \cdots, A_{15}$ ，再由樞紐點按一個單位計分別往樞紐點兩側運送至最終鋪設地點，計算從樞紐點開始的鋪設費用。

雖然準備把問題分解為兩個子問題進行處理，但最終優化時，必須作為一個綜合的優化問題進行處理，否則無法得到全局最優解。

三、模型的建立與求解

記第 $\cdots, 7)$ 個鋼廠的最大供應量為 $s_{i}$ ，從第 i 個鋼廠到鋪設節點 $\cdots, 15)$ 的訂購和運輸費用為 $c_{ij}$ ；用 $lk=∣AkAk+1∣(k=1,2,?,14)l_{k}=|A_{k}A_{k+1}|(k=1, 2, \cdots, 14)$ 表示管道第 k 段需要鋪設的鋼管量。 $x_{ij}$ 是從鋼廠 $S_{i}$ 運到節點 j 的鋼管量， $y_{j}$ 是從節點 j 向左鋪設的鋼管量， $z_{j}$ 是從節點 j 向右鋪設的鋼管量。

根據題中所給數據，可以先計算出從供應點 $S_{i}$ 到需求點 $A_{j}$ 的最小購運費 $c_{ij}$ （即出廠售價與運輸費用之和），再根據 $c_{ij}$ 求解總費用，總費用應包括：訂購費用（已包含在 $c_{ij}$ 中），運輸費用（由各廠 $S_{i}$ 經鐵路、公路至各點 $Aj,i=1,2,?,7A_{j}, i=1, 2, \cdots, 7$ ），鋪設管道 $A_{j}A_{j+1}(j=1, 2, L, 14)$ 的運費。

1.運費矩陣的計算模型

購買單位鋼管及從 $S_{i}(i=1, 2, L, 7)$ 運送到 $A_{j}(j=1, 2, L, 15)$ 的最小購運 $j = 1, 2, L, 15$ 費用 $c_{ij}$ 的計算如下。

(1)計算鐵路任意兩點間的最小運輸費用

由于鐵路運費不是連續的，故不能直接構造鐵路費用賦權圖，用 Floyd 算法來計算任意兩點間的最小運輸費用。但可以首先構造鐵路距離賦權圖，用 Floyd 算法來計算任意兩點間的最短鐵路距離值，再依據題中的鐵路運價表，求出任意兩點間的最小鐵路運輸費用。這就巧妙地避開鐵路運費不是連續的問題。
首先構造鐵路距離賦權圖 $G_{1}=(V, E_{1}, W_{1})$ ，其中 $V={S1,?,S7,A1,?,A15,B1,?,B17}={v1,v2,?,v39}V=\{S_{1}, \cdots, S_{7}, A_{1}, \cdots, A_{15}, B_{1}, \cdots, B_{17}\}=\{v_{1}, v_{2}, \cdots, v_{39}\}$ ，總共 39 個頂點的編號見圖 6.22； $W1=(wij(1))39×39W_{1}=(w_{ij}^{(1)})_{39\times 39}$ ，

$wij(1)={dij(1),vi,vj之間有鐵路直接相連+∞,vi,vj之間沒有鐵路直接相連\boldsymbol {w}_{ij}^{(1)}=\left \{ \begin{aligned} &\boldsymbol {d}_{ij}^{(1)}, \boldsymbol {v}_{i},\boldsymbol {v}_{j}之間有鐵路直接相連\\ &+\infty , \boldsymbol {v}_{i},\boldsymbol {v}_{j}之間沒有鐵路直接相連\end{aligned} \right .$
式中： $d_{ij}^{(1)}$ 表示 $v_{i}, v_{j}$ 兩點之間的鐵路里程。然后應用Floyd算法求得任意兩點間的最短鐵路距離。
根據鐵路運價表，可以得到鐵路費用賦權完全圖 $G~1=(V,E1,W~1)\widetilde{G}_{1}=(V, E_{1}, \widetilde{W}_{1})$ , 其中 $W~1=(cij(1))39×39\widetilde{W}_{1}=(c_{ij}^{(1)})_{39\times 39}$ ,這里 $c_{ij}^{(1)}$ 為第 i , j 頂點間的最小鐵路運輸費用，若兩點間的鐵路距離值為無窮大，則對應的鐵路運輸費用也為無窮大。

(2) 構造公路費用的賦權圖

構造公路費用賦權圖 $G_{2}=(V, E_{2}, W_{2})$ ，其中 V 同上， $W2=(cij(2))39×39W_{2}=(c_{ij}^{(2)})_{39\times 39}$

$cij(2)={0.1dij(2),vi,vj之間有公路相連，+∞,vi,vj之間沒有公路相連，c_{ij}^{(2)}=\left \{ \begin{aligned} &0.1d_{ij}^{(2)},v_{i},v_{j}之間有公路相連，\\ &+\infty ,v_{i},v_{j}之間沒有公路相連，\end{aligned} \right .$
式中： $d_{ij}^{(2)}$ 表示 $v_{i}, v_{j}$ 兩點之間的公路里程。

(3)計算任意兩點間的最小運輸費用

由于可以用鐵路、公路交叉運送，所以任意相鄰兩點間的最小運輸費用為鐵路、公路兩者最小運輸費用的最小值。

構造鐵路公路的混合賦權圖 $W=(c_{ij}^{(3)})_{39\times 39}$ ，其中 $c_{ij}^{(3)}=min(c_{ij}^{(1)}, c_{ij}^{(2)})$ 。

對圖G應用Floyd算法，就可以計算出所有頂點對之間的最小運輸費用，最后提取需要的 $Si(i=1,2,?,7)S_{i}(i=1, 2, \cdots, 7)$ 到 $Aj(j=1,2,?,15)A_{j}(j=1, 2, \cdots, 15)$ 的最小運輸費用 $c~ij\widetilde{c}_{ij}$ （單位：萬元）見表6.11。

									表6.11 最小運費計算結果

170.7	160.3	140.2	98.6	38	20.5	3.1	21.2	64.2	92	96	106	121.2	128	142
215.7	205.3	190.2	171.6	111	95.5	86	71.2	114.2	142	146	156	171.2	178	192
230.7	220.3	200.2	181.6	121	105.5	96	86.2	48.2	82	86	96	111.2	118	132
260.7	250.3	235.2	216.6	156	140.5	131	116.2	84.2	62	51	61	76.2	83	97
255.7	245.3	225.2	206.6	146	130.5	121	111.2	79.2	57	33	51	71.2	73	87
265.7	255.3	235.2	216.6	156	140.5	131	121.2	84.2	62	51	45	26.2	11	28
275.7	265.3	245.2	226.6	166	150.5	141	131.2	99.2	76	66	56	38.2	26	2

任意兩點間的最小運輸費用加上出廠售價，得到單位鋼管從任一個 $Si(i=1,2,?,7)S_{i}(i=1, 2, \cdots, 7)$ 到 $Aj(j=1,2,?,15)A_{j}(j=1, 2, \cdots, 15)$ 的購買和運送最小費用 $c_{ij}$ 。

2.總費用的數學規劃模型

目標函數

(1) 從鋼管廠到各樞紐點 $A_{1}$ , $A2,?,A15A_{2}, \cdots, A_{15}$ 的總購運費用為 $∑i=17∑j=115cijxij\sum \limits _{i=1}^{7}\sum \limits _{j=1}^{15}c_{ij}x_{ij}$
(2)鋪設管道不僅只運輸到樞紐點，而是要運送并鋪設到全部管線，注意到將總量為y $_{j}$ 的鋼管從樞紐點往左運到每單位鋪設點，其運費應為第一公里、第二公里、 $??\cdots \cdots$ 直到第y $_{j}$ 公里的運費之和，即為
$0.1×(1+2+?+yj)=0.12yj(yj+1).\mathbf 0.1\times (1+2+\cdots +y_{j})=\frac {0.1}{2}y_{j}(y_{j}+1).$
從樞紐點 $A_{j}$ 往右也一樣，對應的鋪設費用為
$0.1×(1+2+?+zj)=0.12zj(zj+1).0.1\times (1+2+\cdots +z_{j})=\frac{0.1}{2}z_{j}(z_{j}+1).$
總的鋪設費用為
$0.12∑j=115[yj(yj+1)+zj(zj+1)].\frac{0.1}{2}\sum _{j=1}^{15}[y_{j}(y_{j}+1)+z_{j}(z_{j}+1)].$
因而，總購運費用為
$∑i=17∑j=115cijxij+0.12∑j=115[yj(yj+1)+zj(zj+1)]\sum _{i=1}^{7}\sum _{j=1}^{15}c_{ij}x_{ij}+\frac{0.1}{2}\sum _{j=1}^{15}[y_{j}(y_{j}+1)+z_{j}(z_{j}+1)]$

約束條件
(1) 根據鋼管廠生產能力約束或購買限制，有
$∑j=115xij∈{0}∪[500,si],i=1,2,?,7.\sum_{j=1}^{15} x_{ij} \in \{0\} \cup [500, s_i], \quad i = 1, 2, \cdots, 7.$

(2) 購運量應等于鋪設量
$∑i=17xij=zj+yj,j=1,2,?,15.\sum_{i=1}^{7} x_{ij} = z_j + y_j, \quad j = 1, 2, \cdots, 15.$

(3) 樞紐點間距約束：從兩個相鄰樞紐點分別往右、往左鋪設的總單位鋼管數應等于其間距，即
$zj+yj+1=∣AjAj+1∣=lj,j=1,2,?,14.z_j + y_{j+1} = |A_j A_{j+1}| = l_j, \quad j = 1, 2, \cdots, 14.$

(4) 端點約束：

從樞紐點 $A_{1}$ 只能往右鋪，不能往左鋪，故
$y_{1} = 0,$
從樞紐點 $A_{15}$ 只能往左鋪，不能往右鋪，故
$z_{15} = 0.$

(5) 非負約束：
$xij≥0,yj≥0,zj≥0,i=1,2,?,7,j=1,2,?,15.x_{ij} \ge 0, \quad y_{j} \ge 0, \quad z_{j} \ge 0, \quad i=1, 2, \cdots, 7, \quad j=1, 2, \cdots, 15.$

綜上所述，建立如下數學規劃模型

$min?∑i=17∑j=115cijxij+0.12∑j=115(zj(zj+1)+yj(yj+1)),(6.25)\min\sum _{i=1}^{7}\sum _{j=1}^{15}c_{ij}x_{ij}+\frac {0.1}{2}\sum _{j=1}^{15}(z_{j}(z_{j}+1)+y_{j}(y_{j}+1)),(6.25)$

s.t.
${∑j=115xij∈{0}∪[500,si],i=1,2,?,7,∑i=17xij=zj+yj,j=1,2,?,15,zj+yj+1=lj,j=1,2,?,14,y1=0,z15=0,xij≥0,yj≥0,zj≥0,i=1,2,?,7;j=1,2,?,15.(6.26)\left \{ \begin{aligned} &\sum _{j=1}^{15}x_{ij}\in \{ 0\} \cup [500,s_{i}], & i=1,2,\cdots ,7,\\ &\sum _{i=1}^{7}x_{ij}=z_{j}+y_{j}, & j=1,2,\cdots ,15,\\ &z_{j}+y_{j+1}=l_{j}, & j=1,2,\cdots ,14,\\ &y_{1}=0, z_{15}=0,\\ &x_{ij}\ge 0, y_{j}\ge 0, z_{j}\ge 0, & i=1,2,\cdots ,7; j=1,2,\cdots ,15. \end{aligned} \right .(6.26)$

3.模型求解

使用計算機求解上述數學規劃時，需要對約束條件（6.26）中的第一個非線性約束

$∑j=115xij∈{0}∪[500,si],i=1,2,?,7(6.27)\sum _{j=1}^{15}x_{ij}\in \{ 0\} \cup [500,s_{i}], \quad i=1,2,\cdots ,7 \quad (6.27)$
進行處理。引進0-1變量

$ti={1,鋼管廠?i生產,0,鋼管廠?i不生產,t_{i}=\left \{ \begin{matrix} 1, & \text{鋼管廠 } i \text{ 生產}, \\ 0, & \text{鋼管廠 } i \text{ 不生產}, \end{matrix} \right .$
把約束條件(6.27)轉化為線性約束

$500ti≤∑j=115xij≤siti,i=1,2,?,7.(6.28)500t_{i}\le \sum _{j=1}^{15}x_{ij}\le s_{i}t_{i}, \quad i=1,2,\cdots ,7. \quad (6.28)$

利用 Python 軟件求得總費用的最小值為 127.8632 億。具體的訂購和運輸方案見表 6.12 所示。

	訂購量	$A_{2}$	$A_{3}$	$A_{4}$	$A_{5}$	$A_{6}$	$A_{7}$	$A_{8}$	$A_{9}$	$A_{10}$	$A_{11}$	$A_{12}$	$A_{13}$	$A_{14}$	$A_{15}$
$S_{1}$	800	0	0	319	15	200	266	0	0	0	0	0	0	0	0
$S_{2}$	800	179	321	0	0	0	0	300	0	0	0	0	0	0	0
$S_{3}$	1000	0	187	149	0	0	0	0	664	0	0	0	0	0	0
$S_{4}$	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$S_{5}$	1015	0	0	0	600	0	0	0	0	0	415	0	0	0	0
$S_{6}$	1556	0	0	0	0	0	0	0	0	351	0	86	333	621	165
$S_{7}$	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

鋼管運輸excel文件：https://wwo.lanzouu.com/igf7E33r9uha 密碼:1gni
相應的python代碼如下：

#程序文件anli6_1.py
import cvxpy as cp
import numpy as np
import networkx as nx
import pandas as pds1 = ['S'+str(i) for i in range(1,8)]
s2 = ['A'+str(i) for i in range(1,16)]
s3 = ['B'+str(i) for i in range(1,18)]
L = s1 + s2 + s3   #構造頂點字符列表
G1 = nx.Graph(); G1.add_nodes_from(L)
L1 = [('B1','B3',450),('B2','B3',80),('B3','B5',1150),('B5','B8',1100),('B4','B6',306),('B6','B7',195),('S1','B7',20),('S1','B8',202),('S2','B8',1200),('B8','B9',720),('S3','B9',690),('B9','B10',520),('B10','B12',170),('S4','B12',690),('S5','B11',462),('B11','B12',88),('B12','B14',160),('B13','B14',70),('B14','B15',320),('B15','B16',160),('S6','B16',70),('B16','B17',290),('S7','B17',30)]
G1.add_weighted_edges_from(L1)  #構造鐵路賦權圖
d1 = nx.floyd_warshall_numpy(G1) #求最短距離矩陣
d1 = np.array(d1)  #轉換為array數組
c1 = np.ones(d1.shape)*np.inf
c1[d1==0]=0; c1[(d1>0) & (d1<=300)]=20
c1[(d1>300) & (d1<=350)]=23; c1[(d1>350) & (d1<=400)]=26
c1[(d1>400) & (d1<=450)]=29; c1[(d1>450) & (d1<=500)]=32
c1[(d1>500) & (d1<=600)]=37; c1[(d1>600) & (d1<=700)]=44
c1[(d1>700) & (d1<=800)]=50; c1[(d1>800) & (d1<=900)]=55
c1[(d1>900) & (d1<=1000)]=60; ind=(d1>1000) & (d1<np.inf)
c1[ind]=60+5*np.ceil(d1[ind]/100-10)G2 = nx.Graph()
G2.add_nodes_from(L)
L2 = [('A1','A2',104),('A2','B1',3),('A2','A3',301),('A3','B2',2),('A3','A4',750),('A4','B5',600),('A4','A5',606),('A5','B4',10),('A5','A6',194),('A6','B6',5),('A6','A7',205),('A7','B7',10),('S1','A7',31),('A7','A8',201),('A8','B8',12),('A8','A9',680),('A9','B9',42),('A9','A10',480),('A10','B10',70),('A10','A11',300),('A11','B11',10),('A11','A12',220),('A12','B13',10),('A12','A13',210),('A13','B15',62),('A13','A14',420),('S6','A14',110),('A14','B16',30),('A14','A15',500),('A15','B17',20),('S7','A15',20)]
G2.add_weighted_edges_from(L2)  #構造公路賦權圖
c2 = nx.to_numpy_matrix(G2)  #導出圖G2的鄰接矩陣
c2 = np.array(c2)   #轉換為array數組
c2[c2==0] = np.inf
c3 = np.minimum(c1, 0.1*c2)G3 = nx.Graph(c3)
c4 = nx.floyd_warshall_numpy(G3) #求最短距離矩陣
c5 = c4[:7,7:22]   #提出7行15列的運費數據
f = pd.ExcelWriter('anli6_1.xlsx')
pd.DataFrame(c5).to_excel(f, index=False)s = np.array([800, 800, 1000, 2000, 2000, 2000, 3000])
p = np.array([160, 155, 155, 160, 155, 150, 160])
b = np.array([104, 301, 750, 606, 194, 205, 201,680, 480, 300, 220, 210, 420, 500])
c = np.tile(p,(15,1)).T + c5  #購運費用
x = cp.Variable((7,15), integer=True)  #調整為整型
y = cp.Variable(15, pos=True); z = cp.Variable(15, pos=True)
t = cp.Variable(7, integer=True)
obj = cp.Minimize(cp.sum(cp.multiply(c, x))+0.05*cp.sum(y**2+y+z**2+z))
con = [500*t<=cp.sum(x,axis=1), cp.sum(x,axis=1)<=cp.multiply(s,t),cp.sum(x,axis=0)==y+z, y[1:]+z[:-1]==b,y[0]==0, z[14]==0,t>=0, t<=1, x>=0]
prob = cp.Problem(obj, con); prob.solve(solver='CPLEX')
print('最優值為：', prob.value); print('最優解為：\n', x.value)
sx = np.sum(x.value, axis=1)  
pd.DataFrame(c).to_excel(f, 'Sheet2', index=False)
pd.DataFrame(x.value).to_excel(f, 'Sheet3', index=False)
f.close()