什么是邏輯回歸

邏輯回歸（Logistic Regression）是一種廣泛應用于分類問題的統計學習方法，盡管名字中帶有"回歸"，但它實際上是一種用于二分類或多分類問題的算法。

邏輯回歸通過使用邏輯函數（也稱為 Sigmoid 函數）將線性回歸的輸出映射到 0 和 1 之間，從而預測某個事件發生的概率。

邏輯回歸的應用場景

信用評分：預測貸款申請人的違約風險。
醫療診斷：根據病人的癥狀預測疾病的可能性。
市場營銷：預測用戶是否會點擊廣告或購買產品
垃圾郵件檢測（是垃圾郵件/不是垃圾郵件）
疾病預測（患病/不患病）
客戶流失預測（流失/不流失）

邏輯回歸幾個重要概念

Sigmoid 函數

$$\sigma (x)=\frac{1}{1+e^{?x}}$$
一個簡單的圖形表示，sigmoid函數將輸出映射到了0和1之間，從而預測某個事件發生的概率

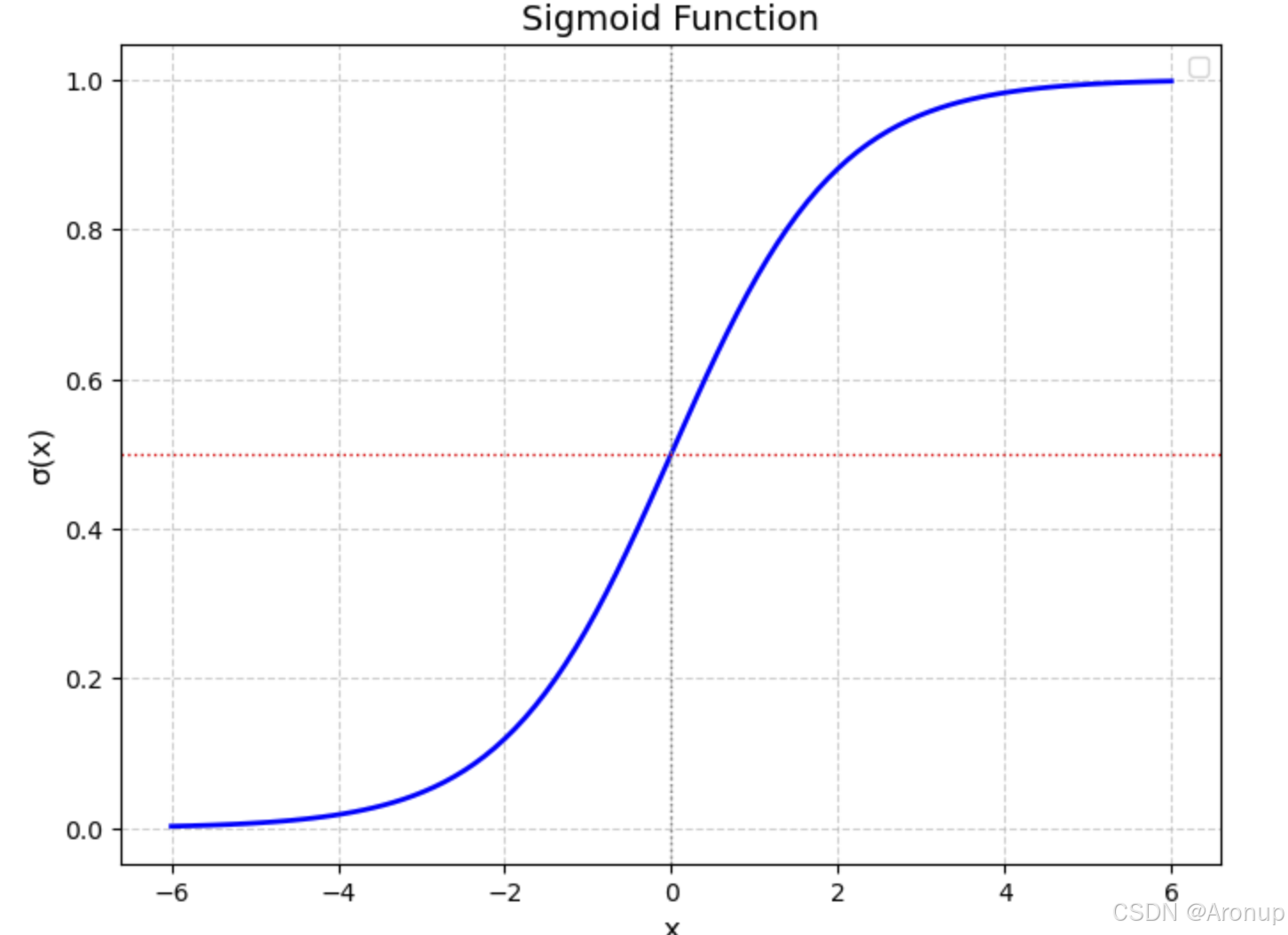
損失函數

是機器學習中用于量化模型預測結果與真實標簽之間差異的數學工具。其核心目標是為模型優化提供一個可計算的目標，通過最小化損失函數，模型能逐步調整參數以逼近真實數據分布
邏輯回歸常用的損失函數是對數損失，又叫交叉熵損失函數，來衡量模型預測的效果。

對于每個樣本，它的損失可以表示為：
$$L(\theta )=?[y_i\log ({\hat{y}}_i)+(1?y_i)\log (1?{\hat{y}}_i)]$$
對整個訓練集的損失是對所有樣本損失的平均：
$$L(\theta )=?\frac{1}{N}\sum _{i=1}^N\left[y_i\log ({\hat{y}}_i)+(1?y_i)\log (1?{\hat{y}}_i)\right]$$
其中 N 是訓練樣本的數量，yi? 是真實標簽，y^?i? 是預測概率值
下面是一個簡單的圖形，p是預測的概率,圖表直觀地展示了當真實標簽固定時，損失如何隨著預測概率的變化而變化

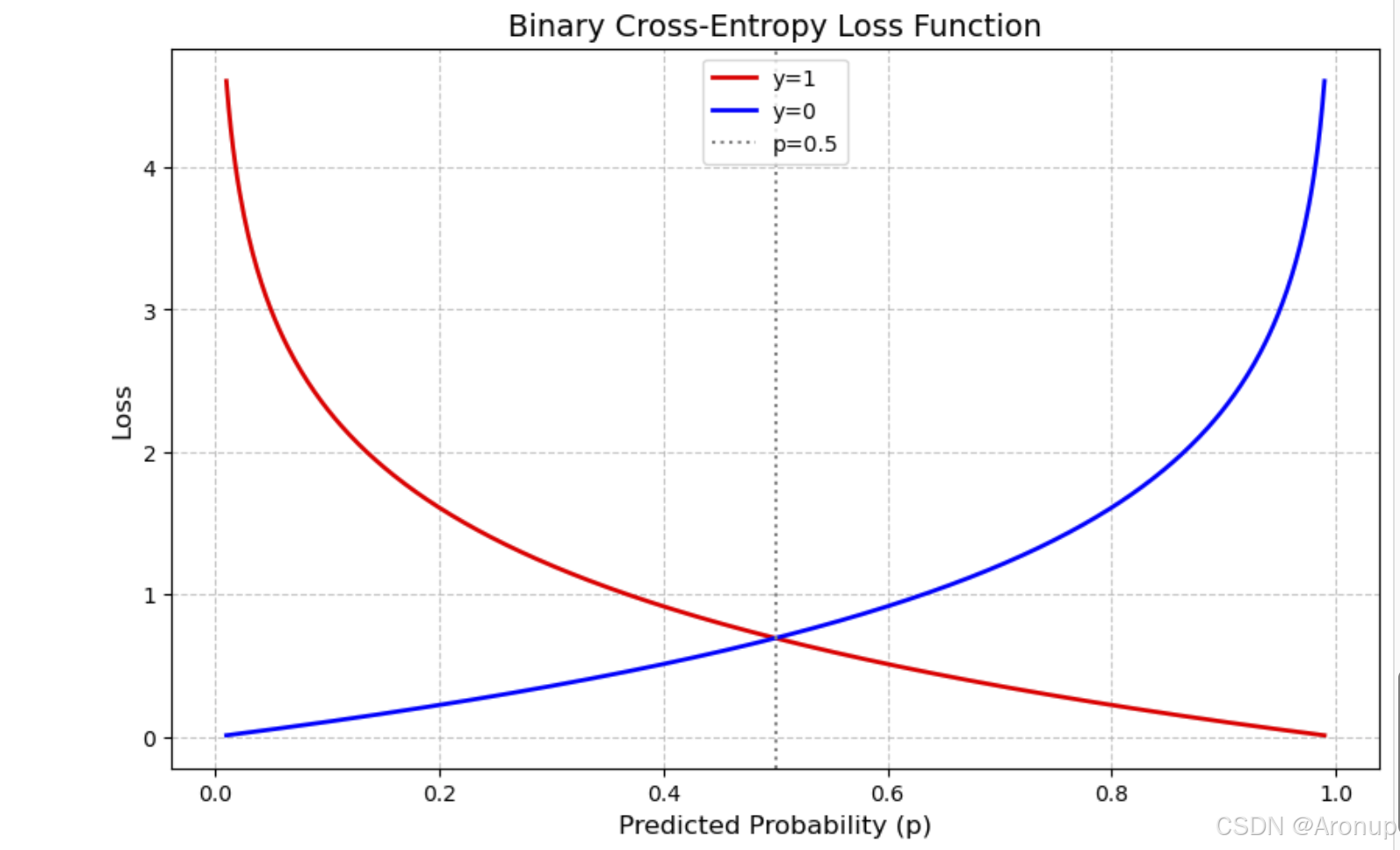
橫軸（Predicted Probability, p）：表示模型預測的概率為正類（通常標記為1）的概率值，范圍從0到1。
縱軸（Loss）：表示對應的損失值，反映了預測概率與真實標簽之間的差異程度。
曲線：
紅色曲線（y=1）：當真實標簽為1時，損失隨預測概率的變化。當預測概率接近0時，損失非常大，因為模型嚴重錯誤地預測了負類。當預測概率接近1時，損失接近0，因為模型正確預測了正類。
藍色曲線（y=0）：當真實標簽為0時，損失隨預測概率的變化。當預測概率接近1時，損失非常大，因為模型嚴重錯誤地預測了正類。當預測概率接近0時，損失接近0，因為模型正確預測了負類。
虛線（p=0.5）：表示預測概率為0.5的位置，此時模型對正負類的預測不確定。

構建邏輯回歸模型的步驟

1.數據EDA
2.特征工程
3.模型構建與訓練
4.模型評估與調優
5.模型解釋與部署

舉個例子

課題：Binary Classification with a Bank Dataset

#邏輯回歸
import numpy as np 
import pandas as pd
from sklearn.linear_model import LogisticRegression# 數據
test = pd.read_csv("../data/BankDataset/test.csv") # 驗證集
train = pd.read_csv("../data/BankDataset/train.csv") # 訓練集
# 合并測試集和訓練集
test['type'] = 'test'
train['type'] = 'train'
all_data = pd.concat([test,train])
all_columns = all_data.columns.tolist()

數據EDA

print(all_columns)
"""
id → ID（標識符/唯一編號）
age → 年齡
job → 職業
marital → 婚姻狀況
education → 教育程度
default → 是否有違約記錄（通常指信貸違約，如“是否拖欠債務”）
balance → 賬戶余額
housing → 是否有住房貸款（或“住房貸款狀態”）
loan → 是否有個人貸款（或“貸款狀態”）
contact → 聯系方式（或“溝通渠道”，如電話、郵件等）
day → 日期（日）（當月中的第幾天）
month → 月份
duration → 通話時長（單位：秒，常見于電話營銷場景）
campaign → 營銷活動次數（客戶被聯系的次數）
pdays → 上次聯系間隔天數（距離上次聯系的間隔天數，999表示未聯系過）
previous → 之前營銷活動次數（客戶在本次活動前參與的營銷次數）
poutcome → 之前營銷結果（如“成功”“失敗”“未響應”等）
y → 目標變量（通常為二分類標簽，如“是否購買產品”“是否響應營銷”）
"""#查看列類型
print("train",all_data.dtypes)
# 缺失值查看
missing_report = pd.DataFrame({'Missing_Count': all_data[all_columns].isnull().sum(),'Missing_Ratio': (all_data[all_columns].isnull().sum() / len(all_data[all_columns])).round(4),'Valid_Count': all_data[all_columns].count(),'Valid_Ratio': (all_data[all_columns].count() / len(all_data[all_columns])).round(4)
})
print(missing_report)# 獲取文本列和數值列
numeric_cols = all_data.select_dtypes(include=['number']).columns.tolist()
non_numeric_cols = all_data.select_dtypes(exclude=['number']).columns.tolist()
# 查看文本特征列的值
for col in non_numeric_cols:print(col)print(all_data[col].unique())

對于一些有順序性的特征進行有序編碼

# 對于一些有順序性的特征進行有序編碼
poutcome_map = {'failure':0,'unknown':1,'other':2,'success':3,None:1} #使用順序編碼，從失敗～成功
default_map={'no':0,'yes':1,None:-1} # 
housing_map={'no':0,'yes':1,None:-1} #
loan_map={'no':0,'yes':1,None:-1} #
education_map = {'primary': 1,'secondary': 2,'tertiary': 3,'unknown': 0
}
order_columns=['poutcome','default','housing','loan','education']
all_data["poutcome_encode"]=all_data['poutcome'].map(poutcome_map)
all_data["default_encode"]=all_data['default'].map(default_map)
all_data["housing_encode"]=all_data['housing'].map(housing_map)
all_data["loan_encode"]=all_data['loan'].map(loan_map)
all_data["education_encode"]=all_data['education'].map(education_map)
#刪除轉換的列
all_data.drop(order_columns,axis=1, inplace=True)

對沒有順序性的列進行獨熱編碼

# 對月份進行標簽編碼
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
all_data['month_encoded'] = le.fit_transform(all_data['month'])
# 對職業進行獨熱編碼編碼
job_dummies = pd.get_dummies(all_data['job'], prefix='job')
job_dummies = job_dummies.astype(int)  # 轉換為0/1
# 對婚姻狀況進行獨熱編碼
marital_dummies = pd.get_dummies(all_data['marital'], prefix='marital')
marital_dummies = marital_dummies.astype(int)  # 轉換為0/1
# 對聯系方式進行獨熱編碼
contact_dummies = pd.get_dummies(all_data['contact'], prefix='contact')
contact_dummies = marital_dummies.astype(int)  # 轉換為0/1

構建新的數據集

# 合并為新的數據集
finall_data=pd.concat([all_data,job_dummies,marital_dummies,contact_dummies],axis=1)
encode_col=['job','marital','contact','month']
finall_data.drop(encode_col,axis=1, inplace=True)
new_train = finall_data[finall_data['type']=='train'].copy()
new_test = finall_data[finall_data['type']=='test'].copy()
new_train.drop(['type'],axis=1, inplace=True)
new_test.drop(['type'],axis=1, inplace=True)
Y_train = new_train['y']
new_train.drop(['y','id'],axis=1, inplace=True)
new_test.drop(['y','id'],axis=1, inplace=True)

構建模型

# 創建模型
from sklearn.linear_model import LogisticRegression
# 創建模型（可調整參數）
model = LogisticRegression(penalty='l2',  # 正則化類型（L1/L2）C=1.0,         # 正則化強度（越小正則化越強）solver='lbfgs', # 優化算法（'lbfgs', 'liblinear', 'saga'）max_iter=1000,  # 最大迭代次數random_state=42
)
#訓練模型
model.fit(new_train,Y_train)

使用模型

y_pred = model.predict(new_test)
submission_df = pd.DataFrame(data={'id': test['id'], 'y': y_pred})
submission_df.to_csv('output.csv', index=False)

參數解釋

penalty（正則化類型）
作用：指定正則化類型，用于防止過擬合。
可選值： ‘l2’（默認）：L2 正則化（權重衰減），對大權重施加懲罰，使參數更平滑。 ‘l1’：L1 正則化，傾向于產生稀疏解（部分參數為零，適用于特征選擇）。 ‘elasticnet’：L1 和 L2 的組合（需額外設置 l1_ratio 參數）。 None：無正則化（不推薦，易過擬合）。
調整建議： 如果特征較多，嘗試 ‘l1’ 進行特征選擇。 默認 ‘l2’ 通常表現穩定

== C（正則化強度）==
作用：控制正則化的強度，與模型復雜度負相關。
取值： 必須為正浮點數（如 C=0.1, C=1.0, C=10）。
越小：正則化越強，模型更簡單（可能欠擬合）。
越大：正則化越弱，模型更復雜（可能過擬合）。
調整建議： 通過交叉驗證（如 GridSearchCV）搜索最優值（例如 C=[0.01, 0.1, 1, 10]）。 默認值 C=1.0 適合多數場景。
solver（優化算法）
作用：指定損失函數的優化算法，不同算法對參數的支持和效率不同。 可選值：
‘lbfgs’（默認）：擬牛頓法，適合中小型數據集，支持 ‘l2’ 和 ‘none’。
‘liblinear’：坐標下降法，適合小型數據集，支持 ‘l1’ 和 ‘l2’。
‘saga’：隨機梯度下降，適合大數據集，支持 ‘l1’、‘l2’ 和’elasticnet’。
‘newton-cg’：牛頓法，支持 ‘l2’ 和 ‘none’。
‘sag’：隨機平均梯度下降，適合大數據集，僅支持 ‘l2’。
調整建議： 數據量小：‘liblinear’ 或 ‘lbfgs’。 數據量大：‘saga’ 或 ‘sag’。 需要 L1 正則化：選擇 ‘liblinear’ 或 ‘saga’。
max_iter（最大迭代次數）
作用：控制優化算法的最大迭代次數，確保算法收斂。
默認值：100（可能不足，尤其是復雜數據）。
調整建議： 如果收斂警告（ConvergenceWarning），增加此值（如 max_iter=1000）。 對于大型模型或高維數據，可能需要更大值（如 5000）。
random_state（隨機種子）
作用：控制隨機數生成，確保結果可復現。
適用場景： 當 solver=‘lbfgs’、‘sag’ 或 ‘saga’ 時，影響權重初始化。在交叉驗證或數據洗牌時固定隨機性。
調整建議： 固定為整數（如 42）以保證結果一致性。

模型優化

努力碼字中…