LeetCode111.二叉樹的最小深度:
題目描述:
給定一個二叉樹,找出其最小深度。
最小深度是從根節點到最近葉子節點的最短路徑上的節點數量。
說明:葉子節點是指沒有子節點的節點。
示例 1:
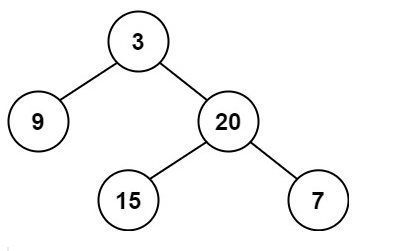
輸入:root = [3,9,20,null,null,15,7]
輸出:2
示例 2:
輸入:root = [2,null,3,null,4,null,5,null,6]
輸出:5
提示:
樹中節點數的范圍在 [0, 10^5] 內
-1000 <= Node.val <= 1000
思路:
涉及樹的左右節點問題,我們可以借鑒閆氏DP的思想,也就是每次只是看當前根節點跟左右子節點(左右子節點下可能存在子樹),我們需要看怎么去維護當前左右子節點的信息
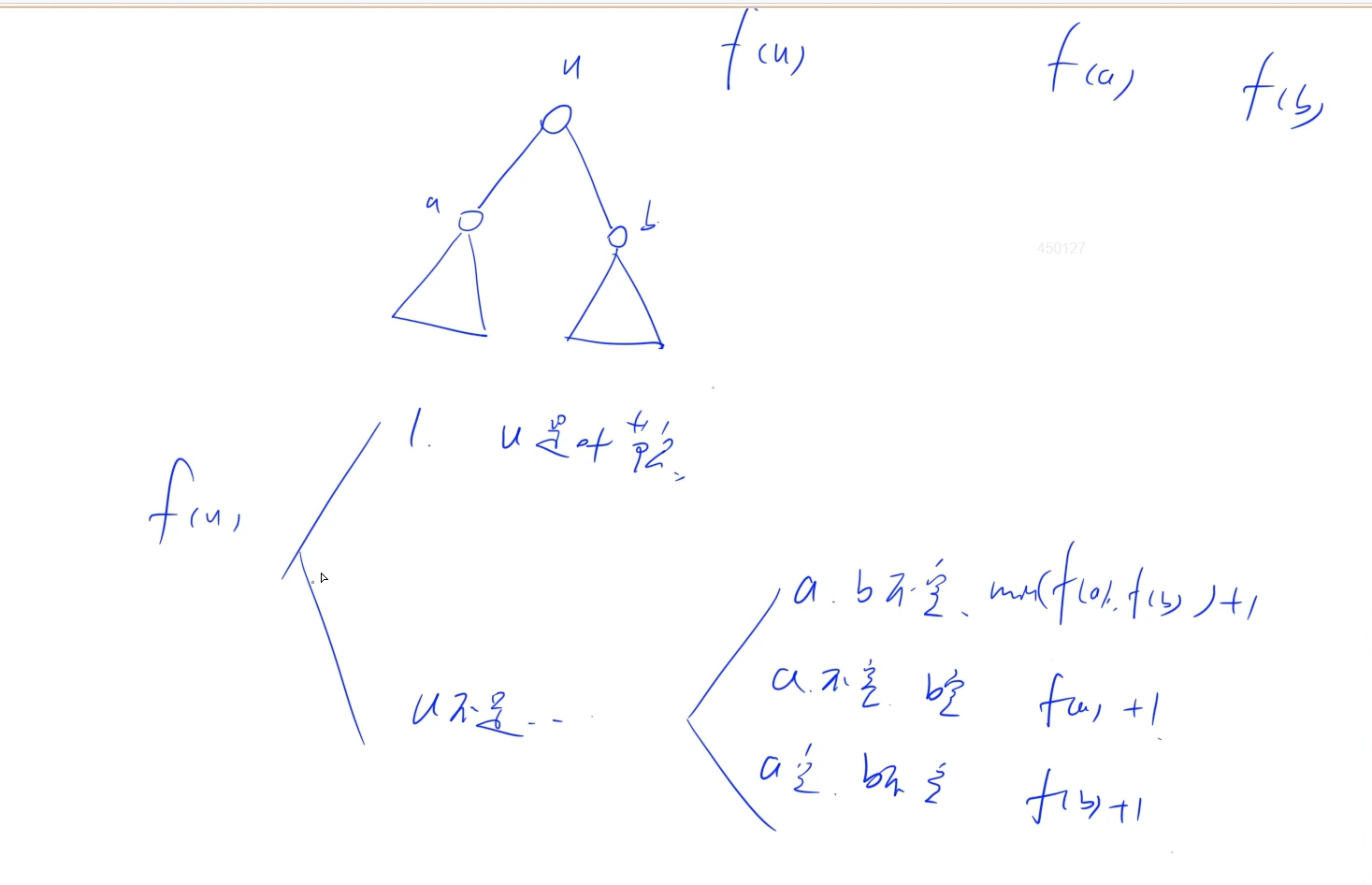
比如這題: 我們需要求的是最小的深度,那么我們就當前根節點以及它的左右子節點來看,根節點的最小深度看成f(n), 左右子節點分別看成f(a), f(b),那么我們可以分情況討論f(n)跟f(a), f(b)之間的關系:
1.a和b都存在: 那么f(n) = min(f(a), f(b)) + 1
2.a存在b不存在: f(n) = min(f(a)) + 1
3.a不存在b存在: f(n) = min(f(b)) + 1
4.a和b都不存在: 那么f(n) = 1
于是我們可以發現當前跟節點的最小深度只跟左右子節點的情況有關,所以我們可以遞歸處理每個子樹的關系,最終將結果聚合到根節點下
時間復雜度:
每個節點會查詢一次,所以總的時間復雜度是O(n)的
注釋代碼:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int minDepth(TreeNode* root) {if(!root) return 0; //當前節點不存在,返回0if(!root -> right && !root -> left) return 1; //沒有左右節點,說明當前是葉子節點if(root -> right && root -> left) return min(minDepth(root -> left), minDepth(root -> right)) + 1; //兩者都存在則返回深度最小的if(root -> left) return minDepth(root -> left) + 1; //存左子節點那么返回左子樹中最小的深度+ 1(當前節點)return minDepth(root -> right) + 1; //否則就是存在右子節點,那么返回右子樹中最小的深度+ 1,以此遞歸}
};
純享版:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int minDepth(TreeNode* root) {if(!root) return 0;if(!root -> left && !root -> right) return 1;if(root -> left && root -> right) return min(minDepth(root -> left), minDepth(root -> right)) + 1;if(root -> left) return minDepth(root -> left) + 1;return minDepth(root -> right) + 1;}
};
LeetCode112.路徑總和:
題目描述:
給你二叉樹的根節點 root 和一個表示目標和的整數 targetSum 。判斷該樹中是否存在 根節點到葉子節點 的路徑,這條路徑上所有節點值相加等于目標和 targetSum 。如果存在,返回 true ;否則,返回 false 。
葉子節點 是指沒有子節點的節點。
示例 1:
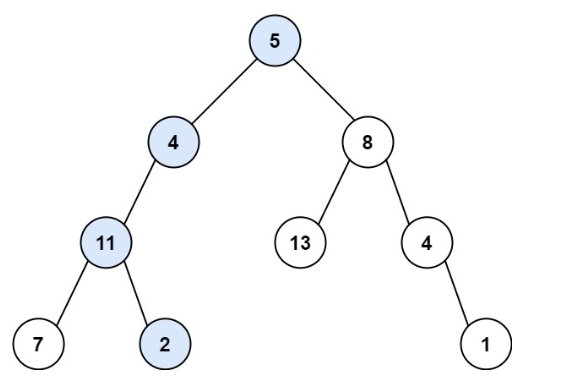
輸入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
輸出:true
解釋:等于目標和的根節點到葉節點路徑如上圖所示。
示例 2:
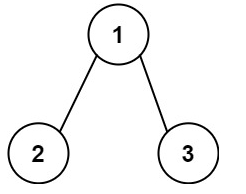
輸入:root = [1,2,3], targetSum = 5
輸出:false
解釋:樹中存在兩條根節點到葉子節點的路徑:
(1 --> 2): 和為 3
(1 --> 3): 和為 4
不存在 sum = 5 的根節點到葉子節點的路徑。
示例 3:
輸入:root = [], targetSum = 0
輸出:false
解釋:由于樹是空的,所以不存在根節點到葉子節點的路徑。
提示:
樹中節點的數目在范圍 [0, 5000] 內
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
思路:
這類需要根據父子節點的值來得出答案的題型一般有兩種思路: 一種自下向上: 就是利用兒子節點來得出父親節點的目標值; 一種是自上向下: 使用父親節點的值來得出兒子節點上的目標值;
這題就是利用自上向下的思路: 設定父節點u, 左右兒子節點分別為a, b : 那么f(a) 和 f(b) 的路徑值就是在父親節點的基礎上加上自己本身的節點值也就是 f(a) = f(u) + a -> val f(b) = f(u) + b -> val 以此類推,直到延展至葉子節點,而這里為了節省變量空間,將原本需要使用sum進行總和累加的變量省去,每次讓targetSum減去當前節點的節點值,然后將減后的targetSum值繼續作為參數傳下去,以此遞歸,直到延展至葉子節點時判斷最后的targetSum是否恰好為0,為0 則說明這條路徑剛好滿足條件,否則說明這條路徑節點值總和不是targetSum
時間復雜度:
每個節點僅被遍歷一次,且遞歸過程中維護 targetSum的時間復雜度是 O(1),所以總時間復雜度是 O(n)
注釋代碼:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if(!root) return false; //如果當前節點不存在返回falsetargetSum -= root -> val; //讓target Sum減去當前節點的值if(!root -> left && !root -> right) return !targetSum; //如果是葉子節點那就判斷當前target Sum的值是否剛好減為0//然后如果當前節點有左兒子或者右兒子,那么在當前節點和targetSum的基礎上遞歸下去return root -> left && hasPathSum(root -> left, targetSum) || root -> right && hasPathSum(root -> right, targetSum);}
};
純享版:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if(!root) return false;targetSum -= root -> val;if(!root -> left && !root -> right && targetSum == 0) return true;return root -> left && hasPathSum(root -> left, targetSum) || root -> right && hasPathSum(root -> right, targetSum);}
};
LeetCode113.路徑總和Ⅱ:
題目描述:
給你二叉樹的根節點 root 和一個整數目標和 targetSum ,找出所有 從根節點到葉子節點 路徑總和等于給定目標和的路徑。
葉子節點 是指沒有子節點的節點。
示例 1:
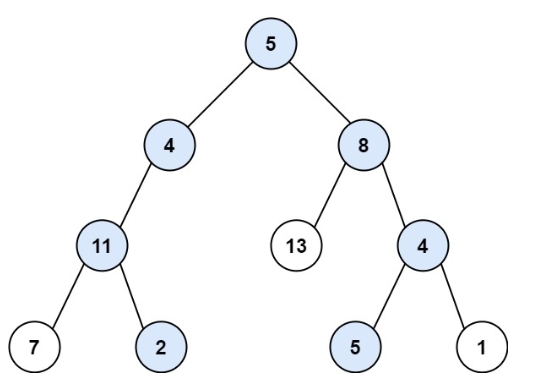
輸入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
輸出:[[5,4,11,2],[5,8,4,5]]
示例 2:
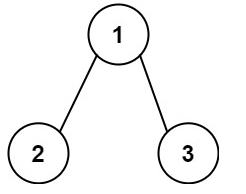
輸入:root = [1,2,3], targetSum = 5
輸出:[]
示例 3:
輸入:root = [1,2], targetSum = 0
輸出:[]
提示:
樹中節點總數在范圍 [0, 5000] 內
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
思路:
跟 LeetCode12.路徑總和 思路一致,但是Ⅰ只要找到合法路徑就return了,Ⅱ則需要將所有的合法路徑存下來, 那么只需要開一個容器并且記錄使得targetSum為0的路徑即可,形式便是dfs形式
時間復雜度:
每個節點會搜一次,并且每個節點上的操作時間是O(1)的,總的時間復雜度就是O(n)的
注釋代碼:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> pathSum(TreeNode* root, int targetSum) {if(root) dfs(root, targetSum);return res;}void dfs(TreeNode* root, int targetSum){path.push_back(root -> val); //將當前節點存入當前路徑targetSum -= root -> val;if(!root -> left && !root -> right) //如果當前節點是葉子節點{if(targetSum == 0) //并且targetSum為0,說明該路徑是合法的{res.push_back(path); //加到答案集合中}}else{if(root -> left) dfs(root -> left, targetSum); //如果不是葉子節點,并且左兒子存在的話遞歸左兒子if(root -> right) dfs(root -> right, targetSum); //不是葉子節點并且右兒子存在的話遞歸右兒子}path.pop_back(); //恢復現場}
};
純享版:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> pathSum(TreeNode* root, int targetSum) {if(root) dfs(root, targetSum);return res;}void dfs(TreeNode* root, int targetSum){path.push_back(root -> val);targetSum -= root -> val;if(!root -> left && !root -> right){if(targetSum == 0) res.push_back(path);}else{if(root -> left) dfs(root -> left, targetSum);if(root -> right) dfs(root -> right, targetSum);}path.pop_back();}
};
LeetCode114.二叉樹展開為鏈表:
題目描述:
給你二叉樹的根結點 root ,請你將它展開為一個單鏈表:
展開后的單鏈表應該同樣使用 TreeNode ,其中 right 子指針指向鏈表中下一個結點,而左子指針始終為 null 。
展開后的單鏈表應該與二叉樹 先序遍歷 順序相同。
示例 1:
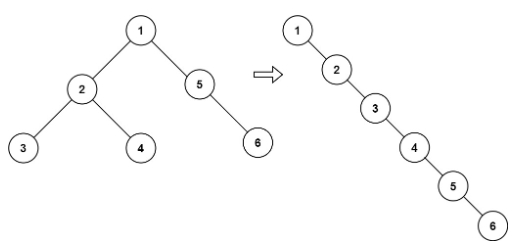
輸入:root = [1,2,5,3,4,null,6]
輸出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
輸入:root = []
輸出:[]
示例 3:
輸入:root = [0]
輸出:[0]
提示:
樹中結點數在范圍 [0, 2000] 內
-100 <= Node.val <= 100
進階:你可以使用原地算法(O(1) 額外空間)展開這棵樹嗎?
思路:
這里是使用二叉樹的前序遍歷:

稍微變形一下就是如果當前節點存在左兒子,就找到當前節點下左子樹的右鏈,將其插入右子樹中,然后跳到右兒子繼續循環處理,直到所有節點都不存在左兒子:
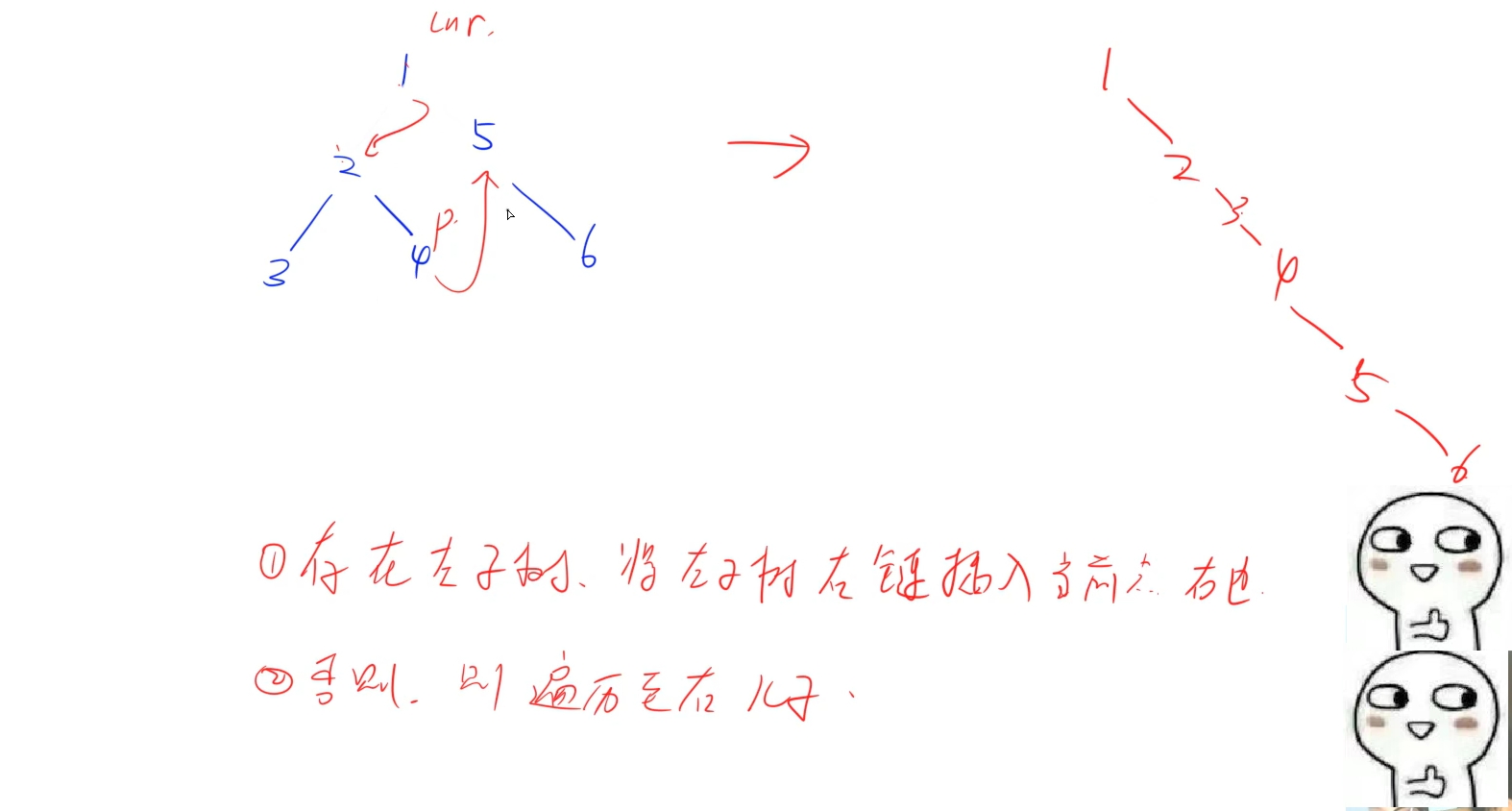
形成鏈表的做法也跟鏈表做法相似: 找到當前節點下的左兒子,以及左子樹的右鏈的最后一個節點,讓左子樹的右鏈最后一個節點右兒子指向當前節點原先的右兒子,再讓當前節點的右兒子指向當前節點的左兒子,具體如上圖所示
時間復雜度:
雖然兩重while循環,但是外層循環會將每個節點遍歷一次,內層循環會將除了根節點之外的其他右鏈內部節點遍歷一次,也就是說每個節點最多遍歷兩次,所以時間復雜度是O(n)的
注釋代碼:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void flatten(TreeNode* root) {while(root){auto p = root -> left; //找到左兒子if(p) //如果存在左兒子,那么找到左兒子下的右鏈{while(p -> right) p = p -> right; //找到左子樹的右鏈p -> right = root -> right; //將右鏈插入右子樹中root -> right = root -> left;root -> left = NULL; //當前節點就沒有左子樹了}root = root -> right; //將當前節點移動到右節點繼續找左子樹的右鏈}}
};
純享版:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void flatten(TreeNode* root) {while(root){auto p = root -> left;if(p){while(p -> right) p = p -> right;p -> right = root -> right;root -> right = root -> left;root -> left = NULL;}root = root -> right;}}
};
LeetCode115.不同的子序列:
題目描述:
給你兩個字符串 s 和 t ,統計并返回在 s 的 子序列 中 t 出現的個數,結果需要對 109 + 7 取模。
示例 1:
輸入:s = “rabbbit”, t = “rabbit”
輸出:3
解釋:
如下所示, 有 3 種可以從 s 中得到 “rabbit” 的方案。

示例 2:
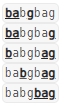
輸入:s = “babgbag”, t = “bag”
輸出:5
解釋:
如下所示, 有 5 種可以從 s 中得到 “bag” 的方案。
提示:
1 <= s.length, t.length <= 1000
s 和 t 由英文字母組成
思路:
諸如此類字符匹配的題型優先考慮用DP:
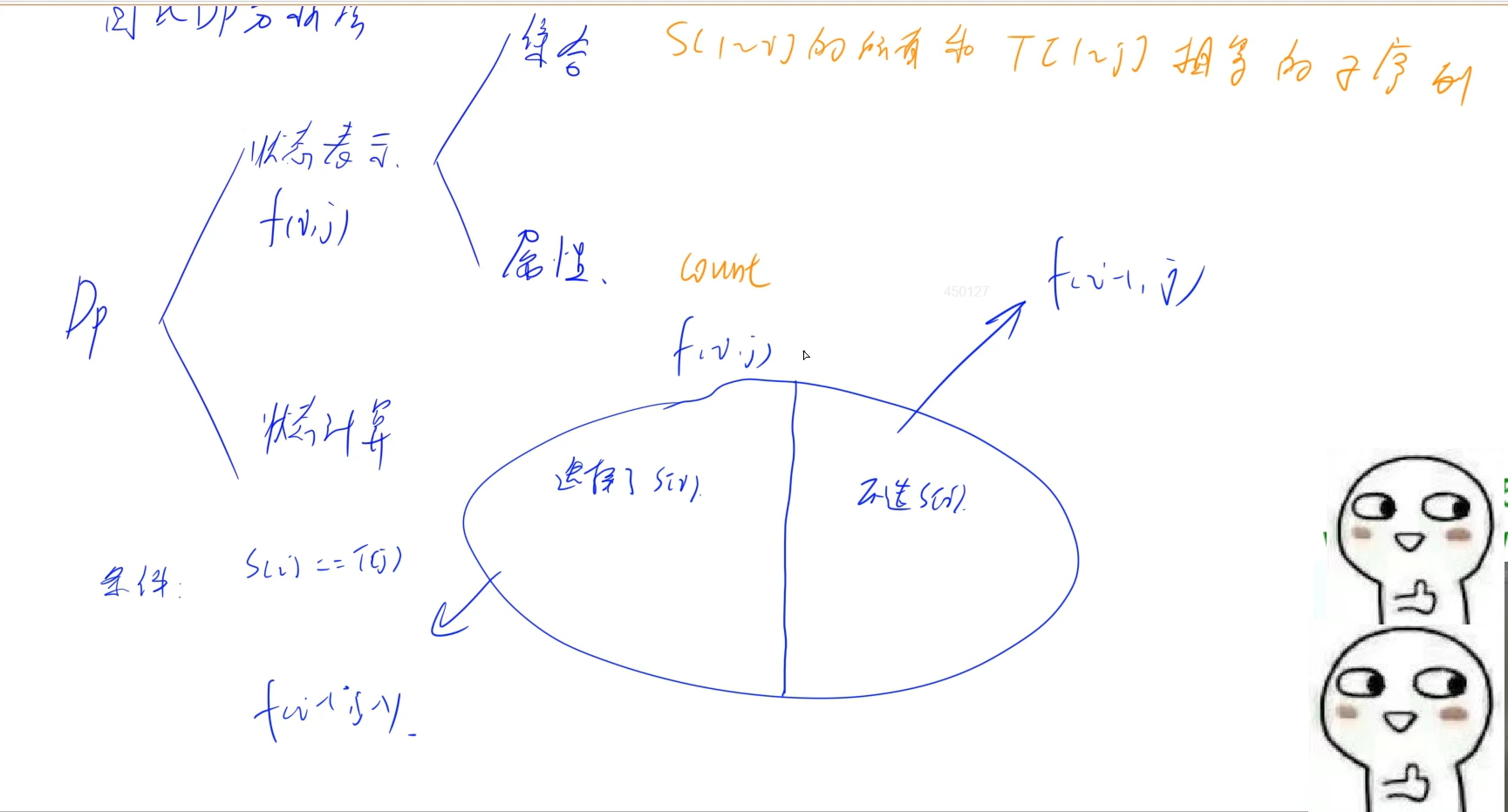
通過閆氏DP法:
1.設定集合f(i, j): 表示由s 的前1 ~i 字符組成的所有跟 t的 1~j字符相同的子序列數量
2.集合劃分: 分情況考慮, DP問題一般對末尾的一位的情況進行討論,這里也是,對于跟t的 1 ~j字符組成的字符串相同的子序列中,是否包含s的第i位進行討論:
(1)不包含s[i]的子序列: 也就是說在不包含s[i]的情況下,所求的f[i][j]也就是由s的1~i字符中組成的子序列中跟t的1~j字符串相同的數量是不包含s[i]的數量,也就等價于求由s的1~i-1字符中組成的子序列中跟t的1~j字符串相同的數量: f[i][j] = f[i - 1][j]
(2)包含s[i]的子序列: 首先要滿足s[i] == t[j]條件,如果選了s[i]那么, 滿足條件的所有子序列都是包含s[i]的,于是變成從s的1~i-1字符中選,讓其組成的子序列中跟t的1~j-1字符組成的字符串相同: f[i][j] += f[i - 1][j - 1](相加是因為滿足條件的子序列可以包含s[i] 也可以不包含s[i])
時間復雜度:O(nm): dp問題一般先分析狀態數量

注釋代碼:
class Solution {
public:const int mod = 1e9 + 7; //設定modint numDistinct(string s, string t) {int n = s.size(), m = t.size();s = ' ' + s, t = ' ' + t; //從1開始比較好處理//設定集合f(i, j)為s的1~i字符組成的所有子序列中等于t的1~j字符串的子序列個數vector<vector<long long>> f(n + 1, vector<long long> (m + 1));for(int i = 0; i <= n; i++) f[i][0] = 1; //s的前1~i個字符選零個來匹配t的前零個字符是一種方案for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){//當不選s的第i個字符,那么s的1 ~i個字符中匹配t的1~j的子序列數量就為s的1~i- 1個字符中匹配t的1~j的子序列數量f[i][j] = f[i - 1][j] % mod; //如果選s的第i個字符, 那么首先判斷s[i] 能不能和t[j]匹配上,如果能匹配上//那么s的1 ~i個字符中匹配t的1~j的子序列數量就要在本身的基礎上加上s的1~i- 1個字符中匹配t的1~j - 1的子序列數量if(s[i] == t[j]) f[i][j] += f[i - 1][j - 1] % mod;}}return f[n][m];}
};
純享版:
class Solution {
public:const int mod = 1e9 + 7;int numDistinct(string s, string t) {int n = s.size(), m = t.size();s = ' ' + s, t = ' ' + t;vector<vector<long long>> f(n + 1, vector<long long> (m + 1));for(int i = 0; i <= n; i++) f[i][0] = 1;for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){f[i][j] = f[i - 1][j] % mod;if(s[i] == t[j]) f[i][j] += f[i - 1][j - 1] % mod;}}return f[n][m];}
};
LeetCode116.填充每個節點的下一個右側節點指針:
題目描述:
給定一個 完美二叉樹 ,其所有葉子節點都在同一層,每個父節點都有兩個子節點。二叉樹定義如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每個 next 指針,讓這個指針指向其下一個右側節點。如果找不到下一個右側節點,則將 next 指針設置為 NULL。
初始狀態下,所有 next 指針都被設置為 NULL。
示例 1:
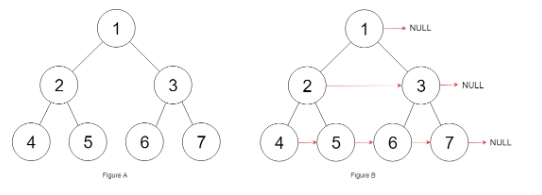
輸入:root = [1,2,3,4,5,6,7]
輸出:[1,#,2,3,#,4,5,6,7,#]
解釋:給定二叉樹如圖 A 所示,你的函數應該填充它的每個 next 指針,以指向其下一個右側節點,如圖 B 所示。序列化的輸出按層序遍歷排列,同一層節點由 next 指針連接,‘#’ 標志著每一層的結束。
示例 2:
輸入:root = []
輸出:[]
提示:
樹中節點的數量在 [0, 2^12 - 1] 范圍內
-1000 <= node.val <= 1000
進階:
你只能使用常量級額外空間。
使用遞歸解題也符合要求,本題中遞歸程序占用的棧空間不算做額外的空間復雜度
思路:
原本這題是可以直接使用層序遍歷的做法直接在每一層進行指向即可,但是進階做法需要使用常數空間的話就只能利用原樹直接進行指向了,那么可以發現每一層的節點指向都需要用到上一層的節點指向才能完整連接每一層的所有節點,而上層又需要更上一層的節點指向,所以我們需要從根節點開始維護,一層一層往下指向:(這里為了通俗易懂些使用樣例進行說明)
1.從根節點1開始,先找到根節點1下最左邊的節點,也就是當前根節點的左兒子2,讓2指向根節點的右兒子3: p -> left -> next = p -> right (p 依次表示上一層的每個節點)
2.進入下一層,同樣是找到下一層的最左邊的節點,也就是上一層節點2的左兒子4: root = root -> left,同樣的讓4指向2的右兒子5
3.由于5需要指向6,這里就需要利用上一層的指向關系: 因為上一層的2后面有指向的節點3:p -> next存在, 則,讓5指向3的左兒子6:p -> left -> next = p -> next -> left, 然后p往后移指向上一層的后一個節點3:p = p -> next, 最后就是讓3的左兒子指向3的右兒子: p -> right -> next = p -> left ,由于上一層節點3的后面沒有后續節點了,所以退出當前層的循環,判斷下一層的最左邊節點是否存在,不存在則無需進入下一層,循環結束
時間復雜度:
每個節點僅會遍歷一次,遍歷時修改指針的時間復雜度是 O(1),所以總時間復雜度是 O(n)
注釋代碼:
/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {if(!root) return root;auto cur = root; //存儲root節點,作為返回while(root -> left){for(auto p = root; p ; p = p -> next) //遍歷當前層的每個節點{p -> left -> next = p -> right; //讓當前節點下的左兒子指向當前節點下的右兒子if(p -> next) p -> right -> next = p -> next -> left; //如果當前節點存在后續節點,則讓當前節點下的右兒子指向當前層的下一個節點的左兒子}root = root -> left; //進入下一層的最左邊節點}return cur;}
};
純享版:
/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {if(!root) return root;auto cur = root;while(root -> left){for(auto p = root; p; p = p -> next){p -> left -> next = p -> right;if(p -> next) p -> right -> next = p -> next -> left;}root = root -> left;}return cur;}
};
LeetCode117.填充每個節點的下一個右側節點指針Ⅱ:
題目描述:
給定一個二叉樹:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每個 next 指針,讓這個指針指向其下一個右側節點。如果找不到下一個右側節點,則將 next 指針設置為 NULL 。
初始狀態下,所有 next 指針都被設置為 NULL 。
示例 1:
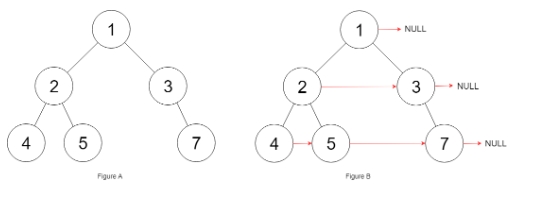
輸入:root = [1,2,3,4,5,null,7]
輸出:[1,#,2,3,#,4,5,7,#]
解釋:給定二叉樹如圖 A 所示,你的函數應該填充它的每個 next 指針,以指向其下一個右側節點,如圖 B 所示。序列化輸出按層序遍歷順序(由 next 指針連接),‘#’ 表示每層的末尾。
示例 2:
輸入:root = []
輸出:[]
提示:
樹中的節點數在范圍 [0, 6000] 內
-100 <= Node.val <= 100
進階:
你只能使用常量級額外空間。
使用遞歸解題也符合要求,本題中遞歸程序的隱式棧空間不計入額外空間復雜度。
思路:
由于這題的進階做法也同樣不能使用額外空間,同時這里還是與上題同樣的思想,使用上一層節點來維護下層的指向關系,但是可能不存在部分節點,就不能使用上題所述方法進行鏈表連接,這里想到只需要創建鏈表的頭尾兩個節點,每次只要發現當前節點有左兒子就優先將左兒子添加到尾節點之前,然后看右兒子,也進行同樣操作,這樣從前往后遍歷上一層的節點,就能將下一層的節點全部依次添加到每層創建的頭尾節點之間
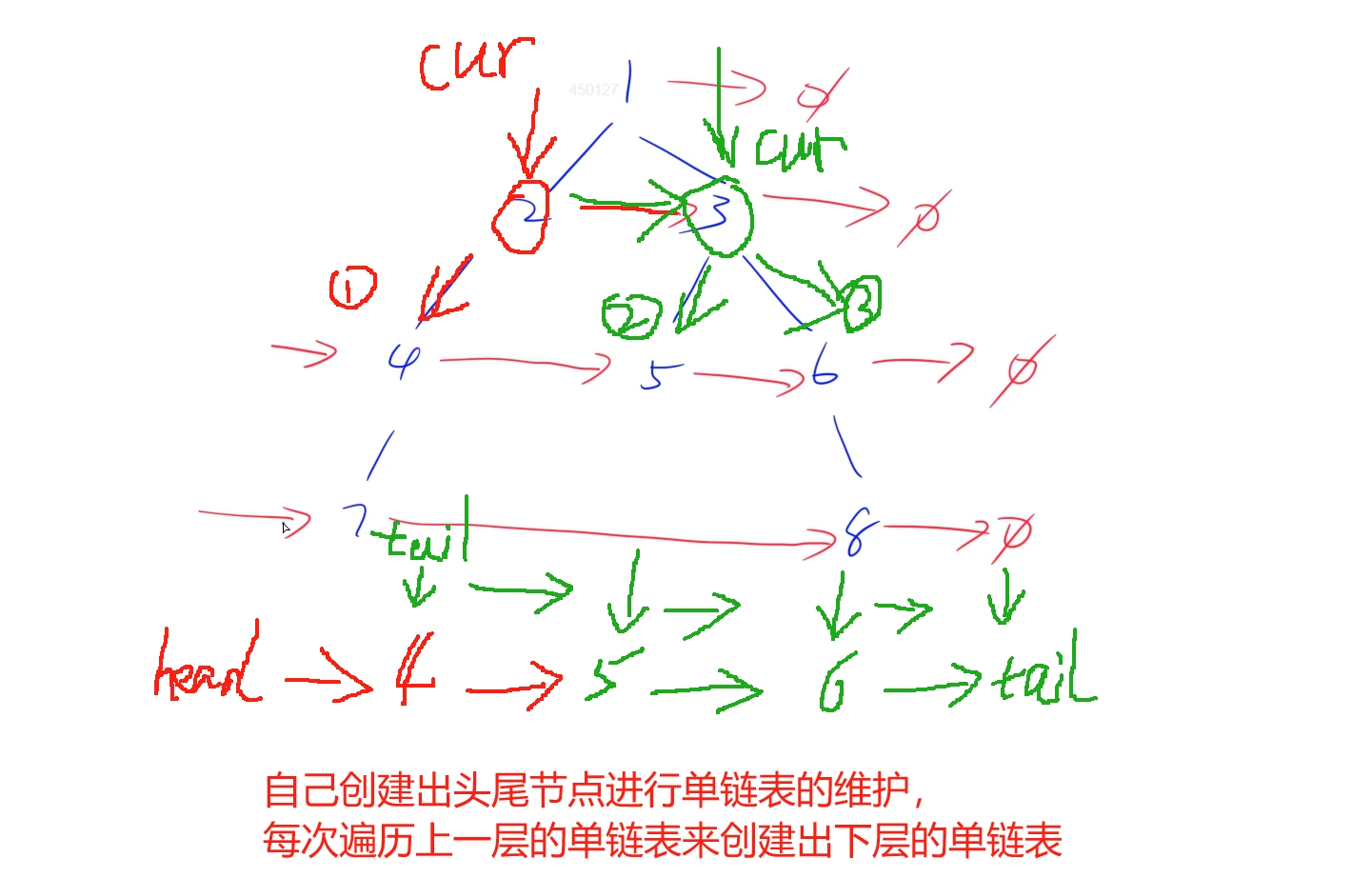
時間復雜度:
每個節點僅會遍歷一次。對于每個節點,遍歷時維護下一層鏈表的時間復雜度是 O(1),所以總時間復雜度是 O(n)。
注釋代碼:
/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {if(!root) return root;auto cur = root;while(cur){auto head = new Node(-1); //每一層的頭節點auto tail = head; //每一層的尾節點for(auto p = cur; p; p = p -> next) //遍歷當前層的每一個節點,利用當前層更新下一層的鏈表指向{if(p -> left) tail = tail -> next = p -> left; //如果存在左兒子那么將左兒子插入尾節點之前if(p -> right) tail = tail -> next = p -> right; //如果存在右兒子那么將右兒子插入尾節點之前}cur = head -> next; //轉至下一層的頭節點下的第一個節點}return root;}
};
純享版:
/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {if(!root) return root;auto cur = root;while(cur){auto head = new Node(-1);auto tail = head;for(auto p = cur; p; p = p -> next){if(p -> left) tail = tail -> next = p -> left;if(p -> right) tail = tail -> next = p -> right;}cur = head -> next;}return root;}
};LeetCode118.楊輝三角:
題目描述:
給定一個非負整數 numRows,生成「楊輝三角」的前 numRows 行。
在「楊輝三角」中,每個數是它左上方和右上方的數的和。
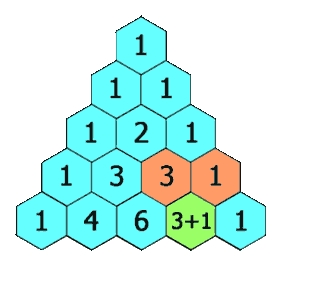
示例 1:
輸入: numRows = 5
輸出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
輸入: numRows = 1
輸出: [[1]]
提示:
1 <= numRows <= 30
思路:
遞推即可:這里主要需要注意的是在轉換成矩陣來看的話當前格子是由上一行的同一列和上一行前一列的兩個格子的和
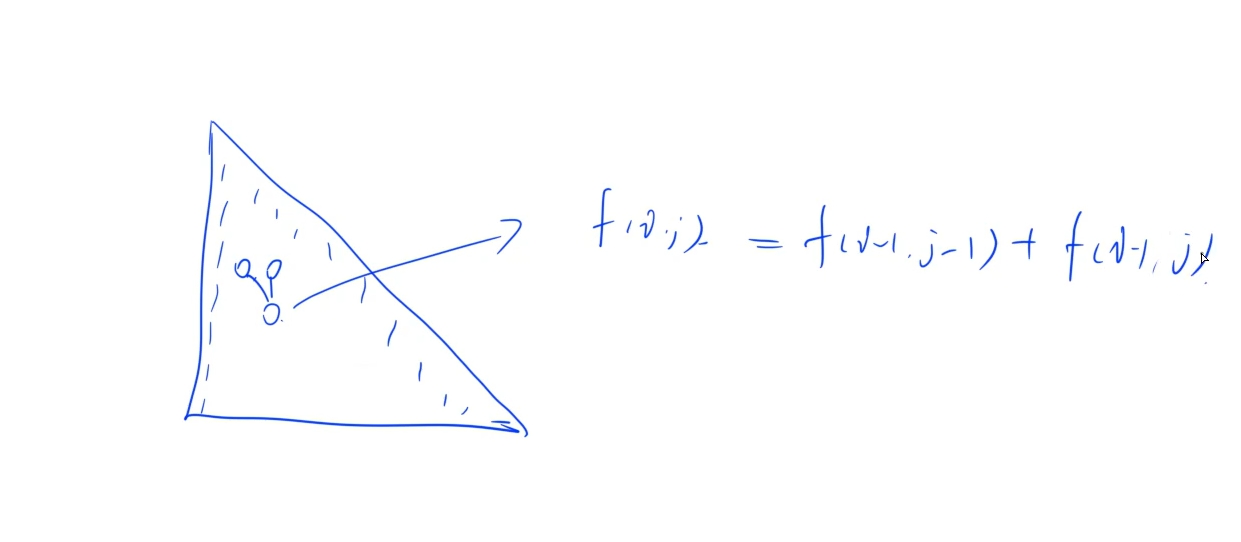
時間復雜度:
總共n行,每行最多n個數,總共n* (n + 1) / 2個數,每個數計算時間是O(1)的,總共的時間復雜度是O(n^2)的
注釋代碼:
class Solution {
public:vector<vector<int>> generate(int n) {vector<vector<int>> f;for(int i = 0; i < n; i++){vector<int> line(i + 1); //每一行的長度line[0] = line[i] = 1; //每一行的開頭和結尾都是1for(int j = 1; j < i; j++) //每一行的每個位置{line[j] = f[i - 1][j - 1] + f[i - 1][j]; //數為上一行同一列和上一行前一列的數之和}f.push_back(line);}return f;}
};
純享版:
class Solution {
public:vector<vector<int>> generate(int n) {vector<vector<int>> res;for(int i = 0; i < n; i++){vector<int> line(i + 1);line[0] = line[i] = 1;for(int j = 1; j < i; j++){line[j] = res[i - 1][j] + res[i - 1][j - 1];}res.push_back(line);}return res;}
};
LeetCode119.楊輝三角Ⅱ:
題目描述:
給定一個非負索引 rowIndex,返回「楊輝三角」的第 rowIndex 行。
在「楊輝三角」中,每個數是它左上方和右上方的數的和。
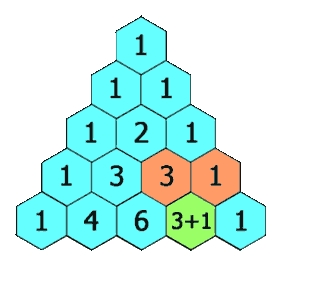
示例 1:
輸入: rowIndex = 3
輸出: [1,3,3,1]
示例 2:
輸入: rowIndex = 0
輸出: [1]
示例 3:
輸入: rowIndex = 1
輸出: [1,1]
提示:
0 <= rowIndex <= 33
進階:
你可以優化你的算法到 O(rowIndex) 空間復雜度嗎?
思路:
正常做法如下所示: 需要O(n*n)的空間復雜度, 進階做法要求使用O(n)的空間復雜度,于是考慮使用滾動數組:
滾動數組:由于我們從狀態方程f[i][j] = f[i - 1][j - 1] + f[i - 1][j]可以看出,當前行的狀態只是跟上一行有關,所以在計算完當前行的狀態值之后, 上一行的狀態值就沒用了,為了節省空間,我們只需要單開兩行(為什么要兩行? 交替存儲當前行的狀態值,計算時不會發生沖突,奇數行和偶數行交替存儲就不會發生覆蓋問題)(怎么存儲? 將當前行區分為奇數行還是偶數行: (i % 2 == 0) -> i & 1: 如果當前行是奇數行,它的狀態值就會存儲到第0行,而利用上一行的狀態值也就是偶數行(第一行)的值,以此交替
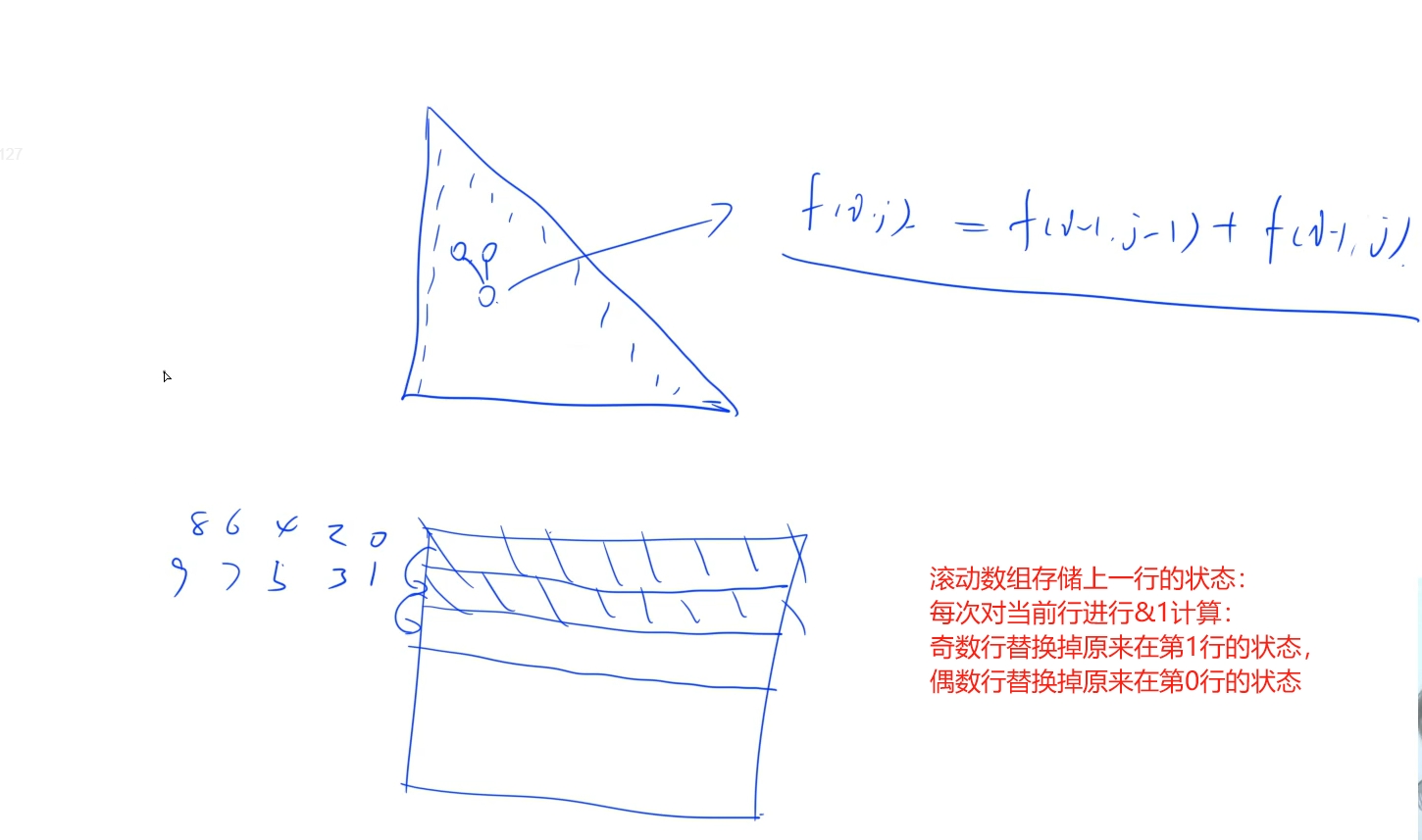
時間復雜度:
總共n層,總共:1 + 2 + …+n = n *(n + 1) / 2個數,每個數的計算時間是O(1)的,總共時間復雜度是O(n * n), 空間復雜度:總共開了2 * n個數組空間,2為常數,所以空間復雜度還是O(n)的
正常做法:
class Solution {
public:vector<int> getRow(int n) {vector<vector<int>> f(n + 1, vector<int> (n + 1));for(int i = 0; i <= n; i++){f[i][0] = f[i][i] = 1;for(int j = 1; j < i; j++){f[i][j] = f[i - 1][j - 1] + f[i - 1][j];}}return f[n];}
};
滾動數組:
class Solution {
public:vector<int> getRow(int n) {vector<vector<int>> f(2, vector<int> (n + 1));for(int i = 0; i <= n; i++){f[i & 1][0] = f[i & 1][i] = 1;for(int j = 1; j < i; j++){f[i & 1][j] = f[i - 1 & 1][j - 1] + f[i - 1 & 1][j];}}return f[n & 1];}
};
LeetCode120.三角形最小路徑和:
題目描述:
給定一個三角形 triangle ,找出自頂向下的最小路徑和。
每一步只能移動到下一行中相鄰的結點上。相鄰的結點 在這里指的是 下標 與 上一層結點下標 相同或者等于 上一層結點下標 + 1 的兩個結點。也就是說,如果正位于當前行的下標 i ,那么下一步可以移動到下一行的下標 i 或 i + 1 。
示例 1:
輸入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
輸出:11
解釋:如下面簡圖所示:
2
3 4
6 5 7
4 1 8 3
自頂向下的最小路徑和為 11(即,2 + 3 + 5 + 1 = 11)。
示例 2:
輸入:triangle = [[-10]]
輸出:-10
提示:
1 <= triangle.length <= 200
triangle[0].length == 1
triangle[i].length == triangle[i - 1].length + 1
-10^4 <= triangle[i][j] <= 10^4
進階:
你可以只使用 O(n) 的額外空間(n 為三角形的總行數)來解決這個問題嗎?
思路:
最小路徑和一看就是DP問題,但是有兩種考慮方式:
1.從最下邊往上:考慮最下邊到上面任意元素的最下路徑,邊界條件比較多,一是要注意兩邊是否存在元素,二是需要判斷路徑是從哪個位置來的
2.從上往下:考慮每個位置到最底層的最小路徑和:
時間復雜度:
每個位置會遍歷到,總的時間復雜度為O(n*n), 空間復雜度:O(1):沒有額外開空間,而是直接將元素位置的值改為當前位置到最底層的最小路徑和
注釋代碼:
class Solution {
public:int minimumTotal(vector<vector<int>>& f) {for(int i = f.size() - 2; i >= 0; i--){for(int j = 0; j <= i; j++){//f[i][j] 替換表示為:從(i, j) 到最底層的最小路徑和f[i][j] += min(f[i + 1][j], f[i + 1][j + 1]);}}return f[0][0]; //返回最上面的點:也就是(0, 0)到最底層的最下路徑和}
};
純享版:
class Solution {
public:int minimumTotal(vector<vector<int>>& f) {for(int i = f.size() - 2; i >= 0; i--){for(int j = 0; j <= i; j++){f[i][j] += min(f[i + 1][j + 1], f[i + 1][j]);}}return f[0][0];}
};
LeetCode121.買賣股票的最佳時機:
題目描述:
給定一個數組 prices ,它的第 i 個元素 prices[i] 表示一支給定股票第 i 天的價格。
你只能選擇 某一天 買入這只股票,并選擇在 未來的某一個不同的日子 賣出該股票。設計一個算法來計算你所能獲取的最大利潤。
返回你可以從這筆交易中獲取的最大利潤。如果你不能獲取任何利潤,返回 0 。
示例 1:
輸入:[7,1,5,3,6,4]
輸出:5
解釋:在第 2 天(股票價格 = 1)的時候買入,在第 5 天(股票價格 = 6)的時候賣出,最大利潤 = 6-1 = 5 。
注意利潤不能是 7-1 = 6, 因為賣出價格需要大于買入價格;同時,你不能在買入前賣出股票。
示例 2:
輸入:prices = [7,6,4,3,1]
輸出:0
解釋:在這種情況下, 沒有交易完成, 所以最大利潤為 0。
提示:
1 <= prices.length <= 10^5
0 <= prices[i] <= 10^4
思路:
相當于上帝視角買股票:只要找到當前i之前最低的時機,每次比較當前i把股票賣出去賺的價值和之前賣股票賺的最大值,同時也要不斷更新當前i之前的最低股票時機,取最小的股票時機
時間復雜度:
依次遍歷每一天,每一天股票價格的計算也是O(1), 的所以總的時間消耗為O(n)
代碼:
class Solution {
public:int maxProfit(vector<int>& prices) {int res = 0;for(int i = 0, minpr = INT_MAX; i < prices.size(); i++){res = max(res, prices[i] - minpr);minpr = min(minpr, prices[i]);}return res;}
};
LeetCode122.買賣股票的最佳時機Ⅱ:
題目描述:
給你一個整數數組 prices ,其中 prices[i] 表示某支股票第 i 天的價格。
在每一天,你可以決定是否購買和/或出售股票。你在任何時候 最多 只能持有 一股 股票。你也可以先購買,然后在 同一天 出售。
返回 你能獲得的 最大 利潤 。
示例 1:
輸入:prices = [7,1,5,3,6,4]
輸出:7
解釋:在第 2 天(股票價格 = 1)的時候買入,在第 3 天(股票價格 = 5)的時候賣出, 這筆交易所能獲得利潤 = 5 - 1 = 4。
隨后,在第 4 天(股票價格 = 3)的時候買入,在第 5 天(股票價格 = 6)的時候賣出, 這筆交易所能獲得利潤 = 6 - 3 = 3。
最大總利潤為 4 + 3 = 7 。
示例 2:
輸入:prices = [1,2,3,4,5]
輸出:4
解釋:在第 1 天(股票價格 = 1)的時候買入,在第 5 天 (股票價格 = 5)的時候賣出, 這筆交易所能獲得利潤 = 5 - 1 = 4。
最大總利潤為 4 。
示例 3:
輸入:prices = [7,6,4,3,1]
輸出:0
解釋:在這種情況下, 交易無法獲得正利潤,所以不參與交易可以獲得最大利潤,最大利潤為 0。
提示:
1 <= prices.length <= 3 * 10^4
0 <= prices[i] <= 10^4
思路:
主要理解題意: 這題可以當天賣當天賣,而且不限制買賣次數,但手上只能持有一支股票,于是我們可以發現,只要即將有虧損就立馬將股票賣出,能盈利的就立馬買入:于是只要記錄每兩天之間是否增加,增就累計,減就不買:
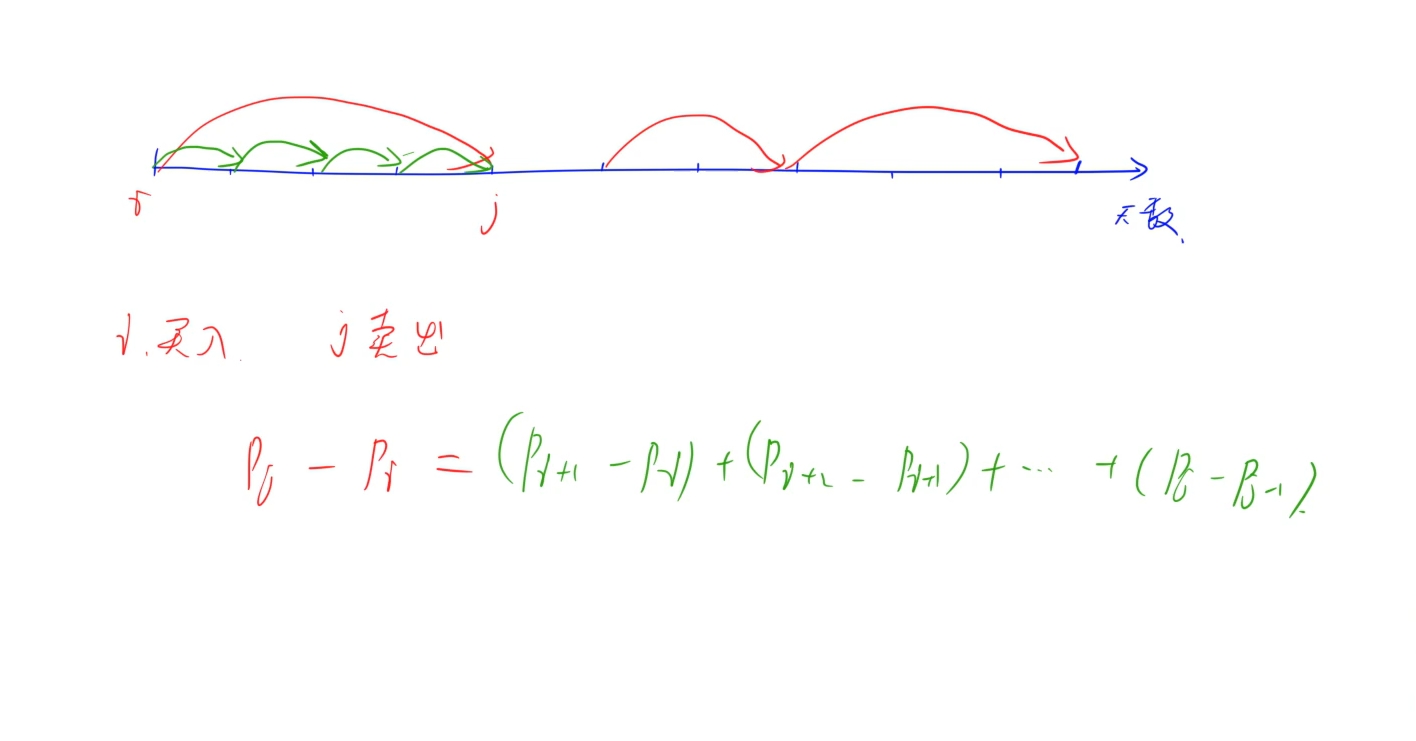
時間復雜度:
每天對比前一天的狀態會計算一次,每次計算是O(1)的, 總共的時間消耗為O(n)
代碼:
class Solution {
public:int maxProfit(vector<int>& prices) {int res = 0;for(int i = 0; i < prices.size() - 1; i++){res += max(0, prices[i + 1] - prices[i]);}return res;}
};
LeetCode123.買賣股票的最佳時機Ⅲ:
題目描述:
給定一個數組,它的第 i 個元素是一支給定的股票在第 i 天的價格。
設計一個算法來計算你所能獲取的最大利潤。你最多可以完成 兩筆 交易。
注意:你不能同時參與多筆交易(你必須在再次購買前出售掉之前的股票)。
示例 1:
輸入:prices = [3,3,5,0,0,3,1,4]
輸出:6
解釋:在第 4 天(股票價格 = 0)的時候買入,在第 6 天(股票價格 = 3)的時候賣出,這筆交易所能獲得利潤 = 3-0 = 3 。
隨后,在第 7 天(股票價格 = 1)的時候買入,在第 8 天 (股票價格 = 4)的時候賣出,這筆交易所能獲得利潤 = 4-1 = 3 。
示例 2:
輸入:prices = [1,2,3,4,5]
輸出:4
解釋:在第 1 天(股票價格 = 1)的時候買入,在第 5 天 (股票價格 = 5)的時候賣出, 這筆交易所能獲得利潤 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接連購買股票,之后再將它們賣出。
因為這樣屬于同時參與了多筆交易,你必須在再次購買前出售掉之前的股票。
示例 3:
輸入:prices = [7,6,4,3,1]
輸出:0
解釋:在這個情況下, 沒有交易完成, 所以最大利潤為 0。
示例 4:
輸入:prices = [1]
輸出:0
提示:
1 <= prices.length <= 10^5
0 <= prices[i] <= 10^5
思路:
兩次!問題思路: 閆氏前后綴分解:將兩次問題拆分開,看出兩次的單獨問題
比如這題: 我們以i為分界,將兩次交易看作: 一次交易是在第i天買入,在i天之后賣出,那么另外一次交易就是在1~i-1天中買入和賣出,這樣的話兩次交易就不會有交錯,同時兩次都是需要取收益最大:
分段分析:
后一次交易比較簡單: 如果在第i天買入,那么在第i天之后找到后面的最大值maxpr 賣出就一定是當前交易收益的最大值:res = maxpr - price[i]
前一次交易: 在1 ~ i- 1天中交易一次獲取交易最大值,跟 買賣股票的最佳時機 一致,當然也可以看成是一個簡單DP問題: 設定集合f[i]表示為在1~i天中買入和賣出一次的收益最大值,那么可以分為在第i天賣出和不在第i天賣出: 首先維護當前i之前的最小價格minpr:
第i天賣出: prices[i] - minpr
不在第i天賣出,那么就表示需要在1 ~ i- 1天中買入和賣出一次,狀態表示為f[i - 1]
最終這一次交易的最大收益就為max(f[i - 1], prices[i] - minpr)
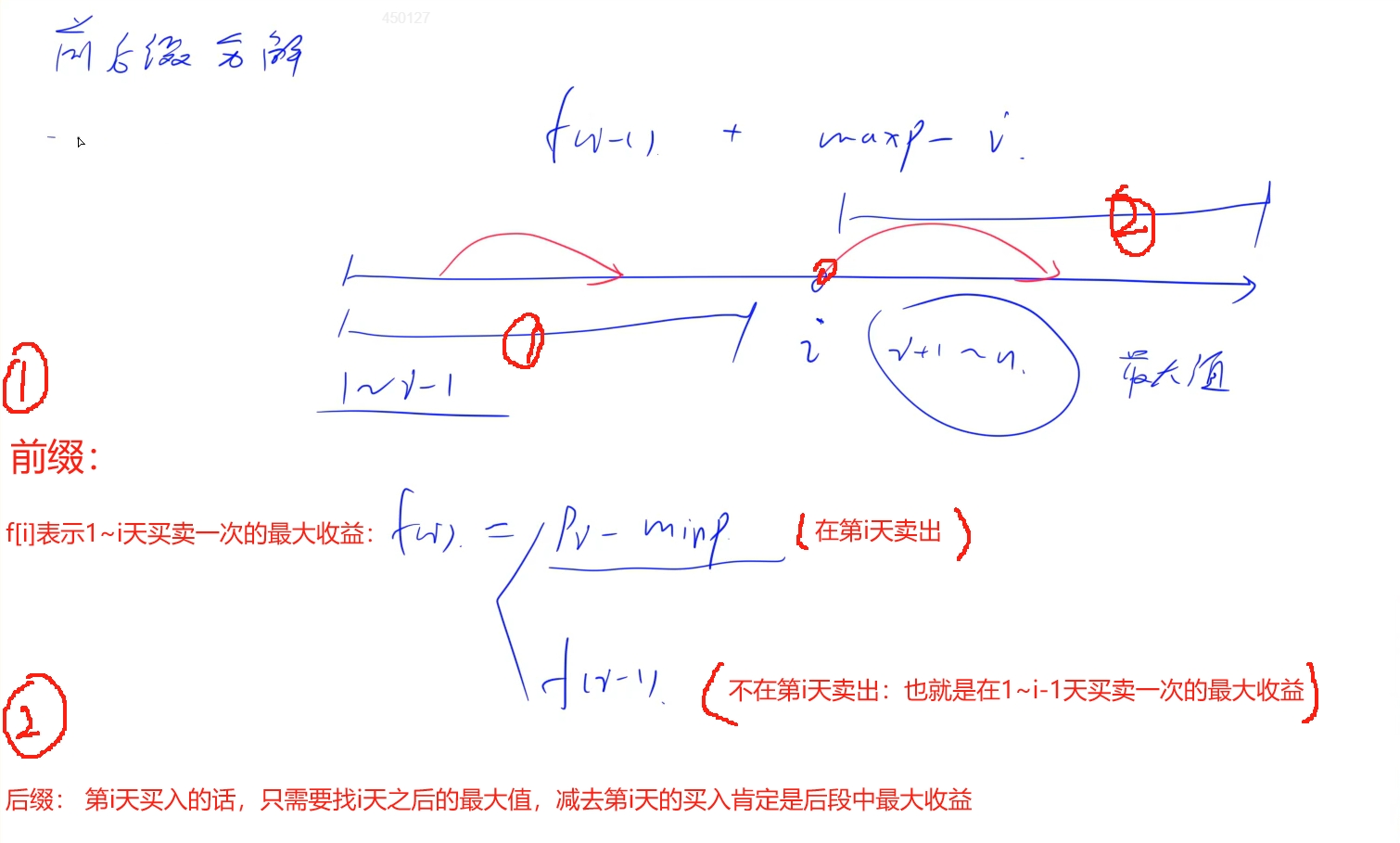
時間復雜度:
兩次交易均遍歷一遍prices數組,每個元素遍歷兩次,所以總的時間復雜度還是O(n)的
注釋代碼:
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size(); //天數vector<int> f(n + 2);//將兩次的交易拆分//將交易第一次: 1~i中買入和賣出一次的最大收益//求出f[i]: 在1~i天中買入和賣出一次的最大收益//從1開始,因為涉及到f[i - 1],0的話會越界,所以將prices向后移一位,f[i] 不變for(int i = 1, minpr = INT_MAX; i <= n; i++){f[i] = max(f[i - 1], prices[i - 1] - minpr);minpr = min(minpr, prices[i - 1]);}int res = 0; //第二次交易是第i天買入,在之后某天賣出//從后往前找到i之后的最大值//因為上面移了一位,所以整體向后移一位for(int i = n, maxpr = 0; i > 0; i--){cout<<i<<endl;res = max(res, maxpr - prices[i - 1] + f[i - 1]); //二次交易加在一起的最大收益maxpr = max(maxpr, prices[i - 1]); //更新i之后的最大價格}return res;}
};
純享版:
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<int> f(n + 2);for(int i = 1, minpr = INT_MAX; i <= n; i++){f[i] = max(f[i - 1], prices[i - 1] - minpr);minpr = min(minpr, prices[i - 1]);}int res = 0;for(int i = n, maxpr = 0; i > 0; i--){res = max(res, maxpr - prices[i - 1] + f[i - 1]);maxpr = max(maxpr, prices[i - 1]);}return res;}
};
LeetCode124.二叉樹的最大路徑和:
題目描述:
二叉樹中的 路徑 被定義為一條節點序列,序列中每對相鄰節點之間都存在一條邊。同一個節點在一條路徑序列中 至多出現一次 。該路徑 至少包含一個 節點,且不一定經過根節點。
路徑和 是路徑中各節點值的總和。
給你一個二叉樹的根節點 root ,返回其 最大路徑和 。
示例 1:
輸入:root = [1,2,3]
輸出:6
解釋:最優路徑是 2 -> 1 -> 3 ,路徑和為 2 + 1 + 3 = 6
示例 2:
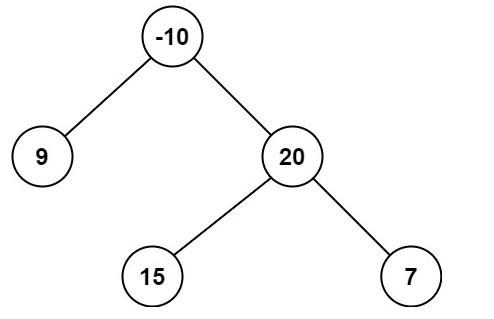
輸入:root = [-10,9,20,null,null,15,7]
輸出:42
解釋:最優路徑是 15 -> 20 -> 7 ,路徑和為 15 + 20 + 7 = 42
提示:
樹中節點數目范圍是 [1, 3 * 10^4]
-1000 <= Node.val <= 1000
思路:
最大路徑并且可以不包含根節點,那么也就是需要搜索每一條路徑,兩個節點之間都存在路徑,常用樹的路徑搜索方式: 枚舉每個節點,考慮以該節點為最高節點(相連)下的所有路徑(如圖所示),這樣的總和就可以找出所有路徑
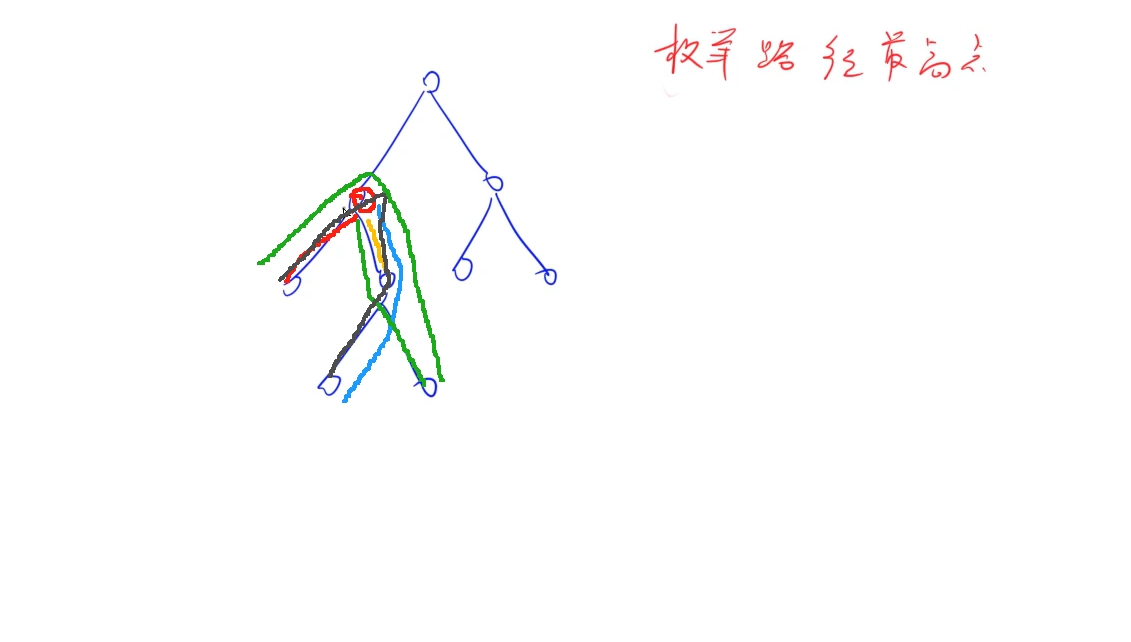
每條路徑找到了,接下來的問題就是如何在這些路徑中找到最大的路徑和,首先統計以每個節點為最高點下的路徑中路徑和的最大值,以某個節點為頂點求其下面的最大值,類似于之前的求根節點下的最大值,做法就是: 獲取到左兒子下的路徑最大值和右兒子下的路徑最大值,那么以當前節點為最高點的路徑和最大值就是當前節點值+ 左兒子下路徑最大值(大于零的前提下)+右兒子下路徑最大值(大于0的前提下),而為了求左右兒子下的路徑最大值,深搜無疑是最好的方式,使用dfs,每次找到當前節點下的左兒子和右兒子的最大路徑和,當前節點最大路徑和就為當前節點值+max(左兒子最大路徑和, 右兒子最大路徑和),以此往下搜即可
時間復雜度:
每個節點搜一次,每次計算時間為O(1),總的時間復雜度為O(n)
注釋代碼:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int ans;int maxPathSum(TreeNode* root) {ans = INT_MIN;dfs(root); //返回以當前節點為最高點下的最大路徑和return ans;}int dfs(TreeNode* u) {if(!u) return 0;int left = max(0, dfs(u -> left)); //返回左邊節點下的最大路徑和int right = max(0, dfs(u -> right)); //返回右邊節點下的最大路徑和ans = max(ans, u -> val + left + right); //答案是在每次節點下左右節點連通之和return u -> val + max(left, right); //當前節點下的最大路徑和為: 當前節點值與max(左邊節點,右邊節點)最大路徑}
};
純享版:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int res;int maxPathSum(TreeNode* root) {res = INT_MIN;dfs(root);return res;}int dfs(TreeNode* u){if(!u) return 0;int l = max(0, dfs(u -> left));int r = max(0, dfs(u -> right));res = max(res, u -> val + l + r);return u -> val + max(l , r);}
};
LeetCode125.驗證回文串:
題目描述:
如果在將所有大寫字符轉換為小寫字符、并移除所有非字母數字字符之后,短語正著讀和反著讀都一樣。則可以認為該短語是一個 回文串 。
字母和數字都屬于字母數字字符。
給你一個字符串 s,如果它是 回文串 ,返回 true ;否則,返回 false 。
示例 1:
輸入: s = “A man, a plan, a canal: Panama”
輸出:true
解釋:“amanaplanacanalpanama” 是回文串。
示例 2:
輸入:s = “race a car”
輸出:false
解釋:“raceacar” 不是回文串。
示例 3:
輸入:s = " "
輸出:true
解釋:在移除非字母數字字符之后,s 是一個空字符串 “” 。
由于空字符串正著反著讀都一樣,所以是回文串。
提示:
1 <= s.length <= 2 * 10^5
s 僅由可打印的 ASCII 字符組成
tolower函數: 可以將大寫字母轉成小寫字母,小寫字母則原樣輸出
思路:
雙指針: 頭尾分別使用兩個指針,只要不是大小寫字母或者數字字符就往中間跳
時間復雜度:s.length是2 * 10^5,使用O(n)的雙指針算法
代碼:
class Solution {
public:bool check(char c){return c >= 'a' && c <= 'z' || c >= 'A' && c <= 'Z'|| c >= '0' && c <= '9';}bool isPalindrome(string s) {for(int i = 0, j = s.size() - 1; i < j; i++, j--){while(i < j && !check(s[i])) i++;while(i < j && !check(s[j])) j--;if(i < j && tolower(s[i]) != tolower(s[j])) return false;}return true;}
};
LeetCode126.單詞接龍Ⅱ:
題目描述:
按字典 wordList 完成從單詞 beginWord 到單詞 endWord 轉化,一個表示此過程的 轉換序列 是形式上像 beginWord -> s1 -> s2 -> … -> sk 這樣的單詞序列,并滿足:
每對相鄰的單詞之間僅有單個字母不同。
轉換過程中的每個單詞 si(1 <= i <= k)必須是字典 wordList 中的單詞。注意,beginWord 不必是字典 wordList 中的單詞。
sk == endWord
給你兩個單詞 beginWord 和 endWord ,以及一個字典 wordList 。請你找出并返回所有從 beginWord 到 endWord 的 最短轉換序列 ,如果不存在這樣的轉換序列,返回一個空列表。每個序列都應該以單詞列表 [beginWord, s1, s2, …, sk] 的形式返回。
示例 1:
輸入:beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
輸出:[[“hit”,“hot”,“dot”,“dog”,“cog”],[“hit”,“hot”,“lot”,“log”,“cog”]]
解釋:存在 2 種最短的轉換序列:
“hit” -> “hot” -> “dot” -> “dog” -> “cog”
“hit” -> “hot” -> “lot” -> “log” -> “cog”
示例 2:
輸入:beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”]
輸出:[]
解釋:endWord “cog” 不在字典 wordList 中,所以不存在符合要求的轉換序列。
提示:
1 <= beginWord.length <= 5
endWord.length == beginWord.length
1 <= wordList.length <= 500
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小寫英文字母組成
beginWord != endWord
wordList 中的所有單詞 互不相同
思路:
使用圖論知識,將開始單詞到結束單詞的所有單詞看成一個點,兩個單詞之間的變換就是邊權為1的邊,
從開始單詞beginWord開始,不斷往后判斷當前單詞(點t)能否由上一個單詞(點r)變換一次(dist[t] == dist[r] + 1)得到,最后變換得到endWord為止
dist存儲當前點到起點的距離,由于題意需要求所有從beginWord到endWord的最短路徑,于是變成圖的最短路問題
時間復雜度:
注釋代碼:
class Solution {
public:unordered_set<string> S; unordered_map<string, int> dist;queue<string> q;vector<vector<string>> ans;vector<string> path;string beginWord;vector<vector<string>> findLadders(string _beginWord, string endWord, vector<string>& wordList) {for(auto word : wordList) S.insert(word);beginWord = _beginWord;dist[beginWord] = 0;q.push(beginWord); //將開始單詞加入while(q.size()){auto t = q.front(); //拿出隊頭q.pop();string r = t; //記錄隊頭防止丟失for(int i = 0; i < t.size(); i++) //對于每一個單詞的每一位{t = r; //重新置為原始的隊頭單詞,不讓上一個字母的改變影響下一個字母的改變for(char j = 'a'; j <= 'z'; j++) //要將當前為變成哪個字母{t[i] = j; //將其中一個字母換掉if(S.count(t) && dist.count(t) == 0) //如果能在字典中找到并且沒有出現過{dist[t] = dist[r] + 1; //建一條邊,說明字典中的這個單詞到隊頭單詞的改變距離為1if(t == endWord) break; //如果換完的單詞為結束單詞,說明已經找完了,breakq.push(t); //不然的話將換完的單詞放到隊列中}}}}if(dist.count(endWord) == 0) return ans; //如果dist中沒有終點,就不用搜索了path.push_back(endWord); //將終點插入路徑dfs(endWord);//從終點開始深度搜索return ans;}void dfs(string t){if(t == beginWord) //搜到開始單詞的話就意味著搜到了一條路徑{reverse(path.begin(), path.end()); //翻轉一下ans.push_back(path); //放入答案集合reverse(path.begin(), path.end()); //翻轉回來,防止下一次dfs亂序}else{string r = t; for(int i = 0; i < t.size(); i++) //看當前t可以從哪些邊過來{t = r;for(char j = 'a'; j <= 'z'; j++){t[i] = j;if(dist.count(t) && dist[t] + 1 == dist[r]) //如果存在這條邊,并且能走到新的t{path.push_back(t); //就將當前的t加入路徑中dfs(t);//并繼續搜索t的下一個邊path.pop_back(); //恢復現場}}}}}
};
純享版:
class Solution {
public:unordered_map<string, int> dist;vector<vector<string>> res;vector<string> path;unordered_set<string> S;string beginWord;queue<string> q;vector<vector<string>> findLadders(string _beginWord, string endWord, vector<string>& wordList) {for(auto word : wordList) S.insert(word);beginWord = _beginWord;dist[beginWord] = 0;q.push(beginWord);while(q.size()){string t = q.front();q.pop();string r = t;for(int i = 0; i < t.size(); i++){t = r;for(char j = 'a'; j <= 'z'; j++){t[i] = j;if(S.count(t) && dist.count(t) == 0){dist[t] = dist[r] + 1;cout<<t<<' ' <<r<<' ';if(t == endWord) break;q.push(t);}}}}if(dist.count(endWord) == 0) return res;path.push_back(endWord);dfs(endWord);return res;}void dfs(string t){if(t == beginWord){reverse(path.begin(), path.end());res.push_back(path);reverse(path.begin(), path.end());}else{string r = t;for(int i = 0; i < t.size(); i++){t = r;for(char j = 'a'; j <= 'z'; j++){t[i] = j;if(dist.count(t) && dist[t] + 1 == dist[r]){path.push_back(t);dfs(t);path.pop_back();}}}}}
};LeetCode127.單詞接龍:
題目描述:
字典 wordList 中從單詞 beginWord 到 endWord 的 轉換序列 是一個按下述規格形成的序列 beginWord -> s1 -> s2 -> … -> sk:
每一對相鄰的單詞只差一個字母。
對于 1 <= i <= k 時,每個 si 都在 wordList 中。注意, beginWord 不需要在 wordList 中。
sk == endWord
給你兩個單詞 beginWord 和 endWord 和一個字典 wordList ,返回 從 beginWord 到 endWord 的 最短轉換序列 中的 單詞數目 。如果不存在這樣的轉換序列,返回 0 。
示例 1:
輸入:beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
輸出:5
解釋:一個最短轉換序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”, 返回它的長度 5。
示例 2:
輸入:beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”]
輸出:0
解釋:endWord “cog” 不在字典中,所以無法進行轉換。
提示:
1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小寫英文字母組成
beginWord != endWord
wordList 中的所有字符串 互不相同
思路:
建圖: 根據單詞之間的變換關系,建立每個單詞到beginWord的變換操作次數,dist存儲當前單詞(節點)跟開始單詞(起點)的距離,通過不斷構建兩點之間的邊,最后找到結束單詞endWord時返回endWord距離開始單詞的距離即可(當然要加1, 因為起點設置的距離為0, 但是題意要求返回包括begin Word在內的長度)
時間復雜度:

注釋代碼:
class Solution {
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {unordered_set<string> S;for(auto word : wordList) S.insert(word);queue<string> q;unordered_map<string, int> dist;dist[beginWord] = 0;q.push(beginWord);while(q.size()){string t = q.front();q.pop();string r = t;for(int i = 0; i < t.size(); i++){t = r;for(char j = 'a'; j <= 'z'; j++){t[i] = j;if(S.count(t) && dist.count(t) == 0){dist[t] = dist[r] + 1;if(t == endWord) return dist[t] + 1; //dist數組就是表示當前單詞跟開始單詞的距離,由于dist[beginWord]是0開始,所以+1q.push(t);}}}}return 0;}
};
純享版:
class Solution {
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {unordered_set<string> S;for(auto word : wordList) S.insert(word);unordered_map<string, int> dist;queue<string> q;dist[beginWord] = 0;q.push(beginWord);while(q.size()){string t = q.front();q.pop();string r = t;for(int i = 0; i < t.size(); i++){t = r;for(char j = 'a'; j <= 'z'; j++){t[i] = j;if(S.count(t) && dist.count(t) == 0) {dist[t] = dist[r] + 1;if(t == endWord) return dist[t] + 1;q.push(t);}}}}return 0;}
};
LeetCode128.最長連續序列:
題目描述:
給定一個未排序的整數數組 nums ,找出數字連續的最長序列(不要求序列元素在原數組中連續)的長度。
請你設計并實現時間復雜度為 O(n) 的算法解決此問題。
示例 1:
輸入:nums = [100,4,200,1,3,2]
輸出:4
解釋:最長數字連續序列是 [1, 2, 3, 4]。它的長度為 4。
示例 2:
輸入:nums = [0,3,7,2,5,8,4,6,0,1]
輸出:9
提示:
0 <= nums.length <= 10^5
-10^9 <= nums[i] <= 10^9
思路:
將全部元素插入哈希表中,然后遍歷查找數組元素,先找到起點: 沒有前面一個數 再找到終點: 沒有后面的一個數,計算兩者中間的長度,然后取最大
時間復雜度:題目要求O(n)
注釋代碼:
class Solution {
public:int longestConsecutive(vector<int>& nums) {unordered_set<int> S;for(auto x : nums) S.insert(x);int res = 0;for(auto x : nums){if(S.count(x) && !S.count(x -1)) //起點:前面沒有元素的話{int y = x;S.erase(x); //找到起點后移除,防止重復查找while(S.count(y + 1)) //終點: 往后移動,直到后面沒有元素{y++;S.erase(y); //}res = max(res, y - x + 1);}}return res;}
};純享版:
class Solution {
public:int longestConsecutive(vector<int>& nums) {unordered_set<int> hash;for(auto x : nums) hash.insert(x);int res = 0;for(auto x : nums){if(hash.count(x) && !hash.count(x -1)){int y = x;hash.erase(x);while(hash.count(y + 1)){y++;hash.erase(y);}res = max(res, y - x + 1);}}return res;}
};
LeetCode129.求根到葉子節點數字之和:
題目描述:
給你一個二叉樹的根節點 root ,樹中每個節點都存放有一個 0 到 9 之間的數字。
每條從根節點到葉節點的路徑都代表一個數字:
例如,從根節點到葉節點的路徑 1 -> 2 -> 3 表示數字 123 。
計算從根節點到葉節點生成的 所有數字之和 。
葉節點 是指沒有子節點的節點。
示例 1:
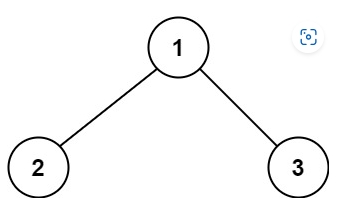
輸入:root = [1,2,3]
輸出:25
解釋:
從根到葉子節點路徑 1->2 代表數字 12
從根到葉子節點路徑 1->3 代表數字 13
因此,數字總和 = 12 + 13 = 25
示例 2:
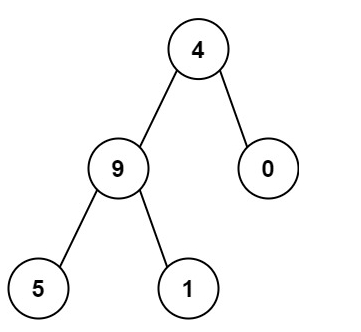
輸入:root = [4,9,0,5,1]
輸出:1026
解釋:
從根到葉子節點路徑 4->9->5 代表數字 495
從根到葉子節點路徑 4->9->1 代表數字 491
從根到葉子節點路徑 4->0 代表數字 40
因此,數字總和 = 495 + 491 + 40 = 1026
提示:
樹中節點的數目在范圍 [1, 1000] 內
0 <= Node.val <= 9
樹的深度不超過 10
思路:
老生常談的做法了,怎么一直不會用? 涉及樹的從根到葉子節點的問題一般只需要考慮局部,就以任意一個節點u以及它的左兒子a, 右兒子b來說,當前u的值可以表示為上面傳下來的number* 10 + 自身節點值,同時呢將這個值傳下去,以此往下推,直到葉子節點則將所有葉子節點下的值累加到一起就是我們的答案
時間復雜度:每個節點搜索一次, 每個節點number的計算時間是O(1)的,總的時間復雜度是O(n)的
注釋代碼:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int res = 0;int sumNumbers(TreeNode* root) {if(root) dfs(root, 0); //從根節點往下搜return res;}void dfs(TreeNode* root, int number){number = number * 10 + root -> val; //當前節點值等于父節點的值*10 + 自身節點值if(!root -> left && !root -> right) res += number; //如果是葉子節點,那么加上這條路徑上的總值if(root -> left) dfs(root -> left, number); //往左兒子搜if(root -> right) dfs(root -> right, number); //往右兒子搜}
};
純享版:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int res = 0;int sumNumbers(TreeNode* root) {if(root) dfs(root, 0);return res;}void dfs(TreeNode* root, int number){number = number * 10 + root -> val;if(!root -> left && !root -> right) res += number;if(root -> left) dfs(root -> left, number);if(root -> right) dfs(root -> right, number);}
};LeetCode130.被圍繞的區域:
題目描述:
給你一個 m x n 的矩陣 board ,由若干字符 ‘X’ 和 ‘O’ 組成,捕獲 所有 被圍繞的區域:
連接:一個單元格與水平或垂直方向上相鄰的單元格連接。
區域:連接所有 ‘O’ 的單元格來形成一個區域。
圍繞:如果您可以用 ‘X’ 單元格 連接這個區域,并且區域中沒有任何單元格位于 board 邊緣,則該區域被 ‘X’ 單元格圍繞。
通過將輸入矩陣 board 中的所有 ‘O’ 替換為 ‘X’ 來 捕獲被圍繞的區域。
示例 1:
輸入:board = [[“X”,“X”,“X”,“X”],[“X”,“O”,“O”,“X”],[“X”,“X”,“O”,“X”],[“X”,“O”,“X”,“X”]]
輸出:[[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“O”,“X”,“X”]]
解釋:
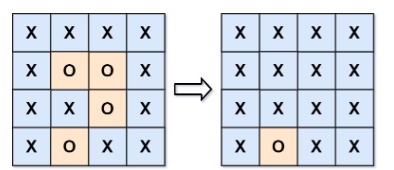
在上圖中,底部的區域沒有被捕獲,因為它在 board 的邊緣并且不能被圍繞。
示例 2:
輸入:board = [[“X”]]
輸出:[[“X”]]
提示:
m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 為 ‘X’ 或 ‘O’
思路:
利用逆向思維:題目要求將所有連通的圍繞O區域換成X,那么我們可以先找到所有沒有被圍繞也就是與邊界相連或者在邊界上的O并替換成#標記出來,通過遍歷將這些區域換回O,而其他的則全部為X:
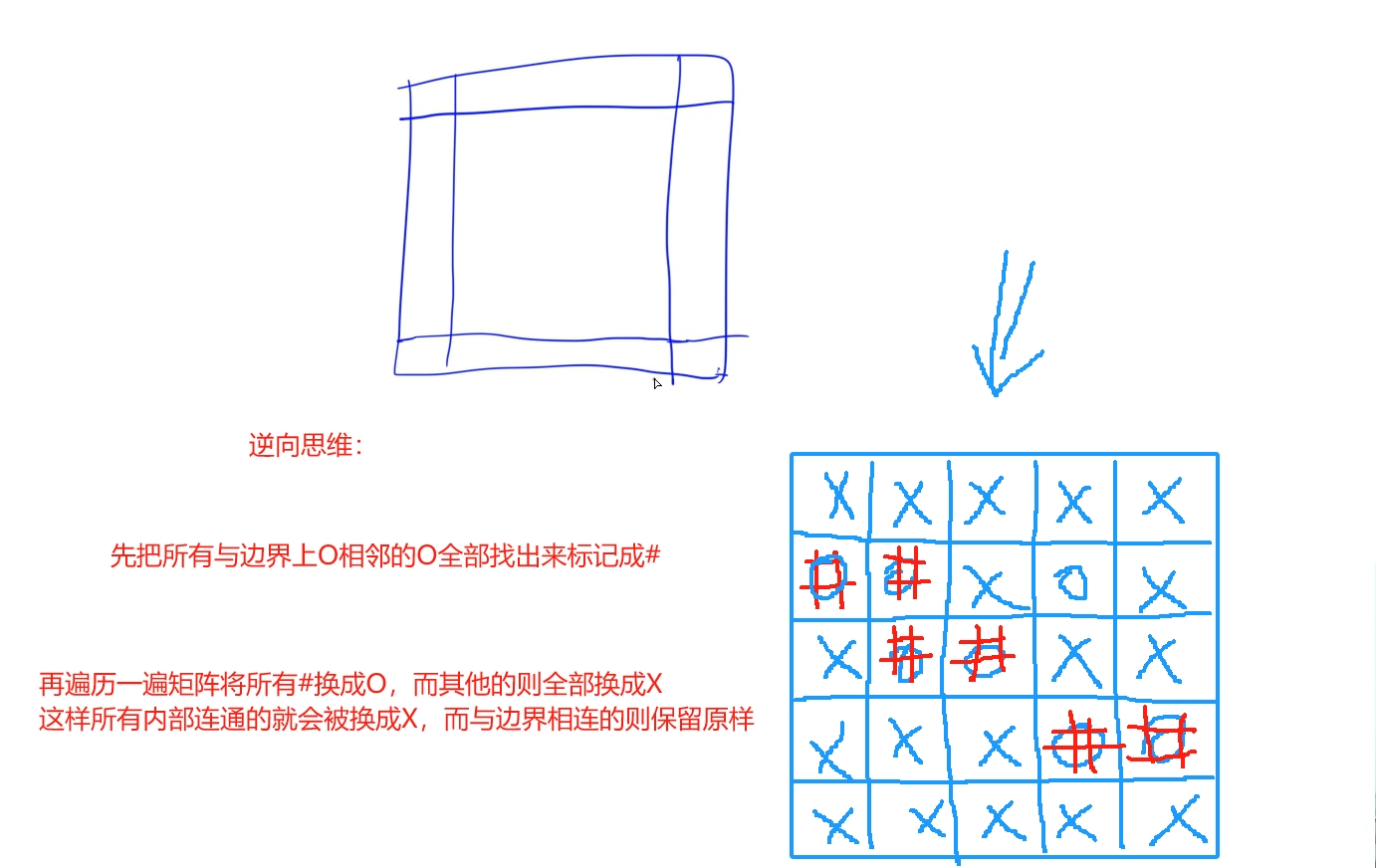
時間復雜度:
每個位置僅被遍歷一次,所以時間復雜度是 O(nm)
注釋代碼:
class Solution {
public:int n, m;vector<vector<char>> board;int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};void solve(vector<vector<char>>& _board) {board = _board;n = board.size();if(!n) return;m = board[0].size();for(int i = 0; i < n; i++) //第一列和最后一列有為O的話,將與該O相連的所有O找出來,標記{if(board[i][0] == 'O') dfs(i, 0);if(board[i][m - 1] == 'O') dfs(i, m - 1);}for(int i = 0; i < m; i++) //第一行和最后一行有為O的話,將與該O相連的所有O找出來,標記{if(board[0][i] == 'O') dfs(0, i);if(board[n - 1][i] == 'O') dfs(n - 1, i);}for(int i = 0;i < n; i++){for(int j = 0; j < m; j++){if(board[i][j] == '#') board[i][j] = 'O'; //將所有與邊緣相連的格子也就是標記為#的格子替換成Oelse board[i][j] = 'X'; //否則替換成X}}_board = board;}void dfs(int x, int y){board[x][y] = '#'; //將當前格子替換成#for(int i = 0; i < 4; i++){int a = x + dx[i], b = y + dy[i];if(a >= 0 && a < n && b >= 0 && b < m && board[a][b] == 'O') //找到所有連在一起的O{dfs(a, b); //繼續找下一個格子}}}
};純享版:
class Solution {
public:vector<vector<char>> board;int n, m;int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};void solve(vector<vector<char>>& _board) {board = _board;n = board.size();if(!n) return;m = board[0].size();for(int i = 0; i < n; i++){if(board[i][0] == 'O') dfs(i, 0);if(board[i][m - 1] == 'O') dfs(i, m - 1);}for(int i = 0; i < m; i++){if(board[0][i] == 'O') dfs(0, i);if(board[n - 1][i] == 'O') dfs(n - 1, i);}for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){if(board[i][j] == '#') board[i][j] = 'O';else board[i][j] = 'X';}}_board = board;}void dfs(int x, int y){board[x][y] = '#';for(int i = 0; i < 4; i++){int a = x + dx[i], b = y + dy[i];if(a >= 0 && a < n && b >= 0 && b < m && board[a][b] == 'O'){dfs(a, b);}}}
};
2024/12/27二刷:
class Solution {
public:vector<vector<char>> board;int n, m;int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, -1, 0, 1};void solve(vector<vector<char>>& _board) {board = _board;n = board.size(), m = board[0].size();for(int i = 0; i < n; i++) //第一列和最后一列的邊緣連通塊{if(board[i][0] == 'O') dfs(i, 0);if(board[i][m - 1] == 'O') dfs(i, m - 1);}for(int i = 0; i < m; i++) //第一行和最后一行的邊緣連通塊{if(board[0][i] == 'O') dfs(0, i);if(board[n - 1][i] == 'O') dfs(n - 1, i);}for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){if(board[i][j] == '#') board[i][j] = 'O'; //將邊緣的連通塊保留下來else board[i][j] = 'X'; //其他連通塊填成X}}_board = board;}void dfs(int x, int y) //找到以x,y為起點的連通塊{board[x][y] = '#';for(int i = 0; i < 4; i++){int a = x + dx[i], b = y + dy[i];if(a >= 0 && a < n && b >= 0 && b < m && board[a][b] == 'O'){dfs(a, b);}}}
};
*注:上述題解均來自acwing課程講解截圖,僅作為學習交流,不作為商業用途,如有侵權,聯系刪除。
Crypto節點、js timestamp代碼、Crypto node)






: 論文解讀)









)
)
