溫馨提示：
本篇文章已同步至"AI專題精講" EAGLE-2：通過動態草稿樹加速語言模型推理

摘要

現代 Large Language Models（LLMs）的推理過程既昂貴又耗時，而 speculative sampling 已被證明是一種有效的解決方案。大多數 speculative sampling 方法（例如 EAGLE）使用靜態的 draft tree，并默認 draft token 的接受率僅依賴于其位置。有趣的是，我們發現 draft token 的接受率也依賴于上下文。本文在 EAGLE 的基礎上提出了 EAGLE-2，該方法引入了一種新的 上下文感知動態 draft tree 技術用于 draft 建模。該改進利用了 EAGLE 的 draft 模型良好校準的特點：draft 模型的置信得分可以以較小誤差逼近 token 的接受率。我們在三個系列的 LLM 和六個任務上進行了廣泛評估，EAGLE-2 達到 3.05× 到 4.26× 的加速比，比 EAGLE-1 快 20%-40%。EAGLE-2 同時確保生成文本的分布保持不變，因此是一種 無損加速算法。

1. 引言

現代 Large Language Models（LLMs）（OpenAI, 2023；Touvron 等，2023）展現出了驚人的能力，并被廣泛應用于各類場景。然而，其參數規模已大幅增長，甚至超過千億。在自回歸生成過程中，每生成一個 token 都需要訪問全部模型參數。一次對話中可能會生成數百到數千個 token，這使得 LLM 推理過程既慢又昂貴Speculative sampling方法（Leviathan 等，2023；Chen 等，2023a）旨在解決這一問題，其核心思想是快速生成一批 draft token，并并行驗證這些 token。通過在單次前向傳播中生成多個 token，這些方法顯著減少了推理延遲。

標準的 speculative sampling 方法（Leviathan et al., 2023；Chen et al., 2023a）使用鏈式結構的 draft。為了提高被接受的 token 序列長度，近期的 speculative sampling 工作引入了樹狀結構的 draft。Sequoia（Chen et al., 2024）顯式地假設 draft token 的接受率僅依賴于其在樹中的位置。EAGLE（Li et al., 2024b）和 Medusa（Cai et al., 2024）在所有上下文中使用相同的靜態 draft tree 結構：在 draft 階段的第 i 步，添加 k 個候選 token，且 k 為固定值。這種做法隱含地采納了上述假設。然而，這一假設似乎與 speculative sampling 的基本直覺相矛盾：某些 token 更容易預測，較小的模型就能準確地預測它們。我們的實驗（見第 3.1 節）表明，draft token 的接受率不僅依賴于其位置，還高度依賴于上下文。因此，靜態 draft tree 結構存在內在的局限性。根據不同上下文中 draft token 的接受率動態調整 draft tree 的結構，能夠取得更好的效果。

然而，獲取 draft token 的接受率需要原始 LLM 的前向計算結果，這與 speculative sampling 減少原始 LLM 前向調用次數的目標相沖突。幸運的是，我們發現 EAGLE 的置信度校準效果良好：draft 模型的置信分數（即概率）可以很好地近似 draft token 的接受率（見第 3.2 節）。這使得基于上下文的動態 draft tree 結構成為可行的選擇。

我們提出 EAGLE-2，該方法利用 draft 模型的置信分數來近似接受率。在此基礎上，它動態調整 draft tree 的結構，從而提升被接受的 token 數量。我們在六個任務上進行了全面且廣泛的測試：多輪對話、代碼生成、數學推理、指令跟隨、文本摘要以及問答任務。所使用的數據集包括：MT-bench（Zheng et al., 2023）、HumanEval（Chen et al., 2021）、GSM8K（Cobbe et al., 2021）、Alpaca（Taori et al., 2023）、CNN/Daily Mail（Nallapati et al., 2016）以及 Natural Questions（Kwiatkowski et al., 2019）。對比方法涵蓋了六種先進的 speculative sampling 技術：標準 speculative sampling（Leviathan et al., 2023；Chen et al., 2023a；Joao Gante, 2023）、PLD（Saxena, 2023）、Medusa（Cai et al., 2024）、Lookahead（Fu et al., 2023）、Hydra（Ankner et al., 2024）以及 EAGLE（Li et al., 2024b）。實驗基于三類 LLM 系列：Vicuna、LLaMA2-Chat 和 LLaMA3-Instruct。

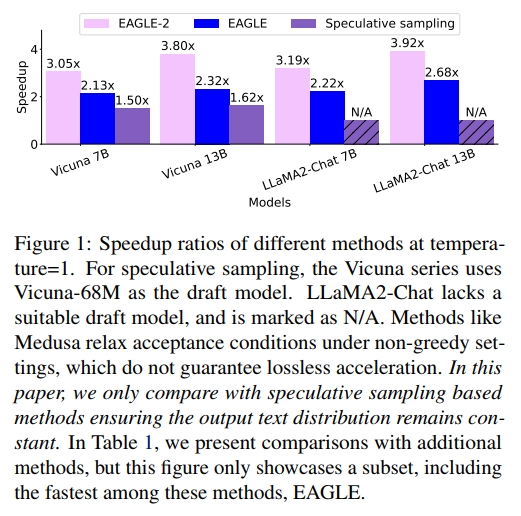
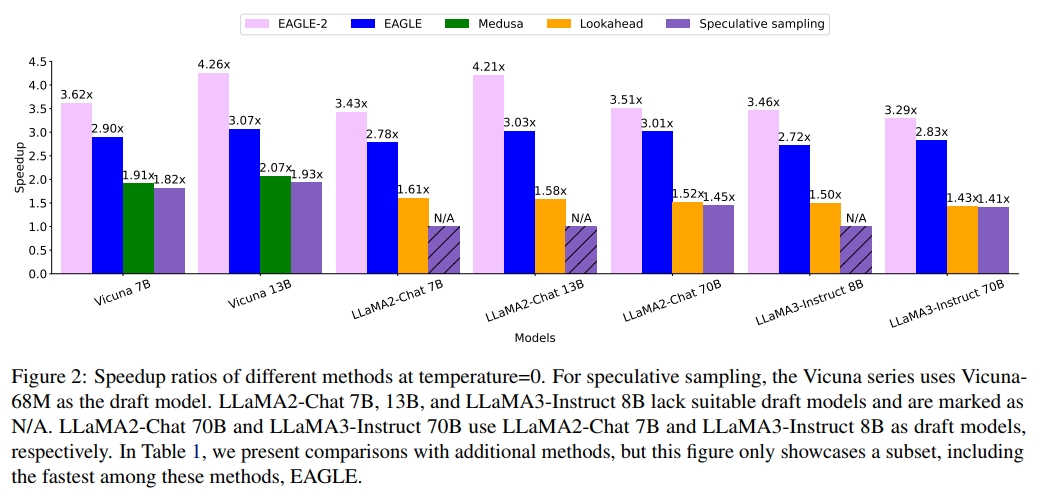
在所有實驗中，EAGLE-2 表現最佳，取得了 2.5 倍到 5 倍的加速效果。圖 1 和圖 2 展示了 EAGLE-2 與其他 speculative sampling 方法在 MT-bench 上的加速比。MT-bench 是一個多輪對話數據集，非常貼近 ChatGPT 等模型的真實應用場景，并被廣泛用于評估最先進的開源或閉源模型。在 MT-bench 數據集上，EAGLE-2 的速度大約是 Medusa 的 2 倍，約為 Lookahead 的 2.3 倍，同時確保輸出分布保持不變。

除了性能表現之外，EAGLE-2 還具有以下優勢：

• 開箱即用。相比 EAGLE，EAGLE-2 無需訓練任何額外的模型。它不需要訓練一個單獨的模型來預測 draft tree 結構，而是基于 draft 模型的置信分數動態調整 draft tree 結構，這一點對于 speculative sampling 至關重要。因此，EAGLE-2 完全無需額外訓練。

• 可靠性。EAGLE-2 不對原始 LLM 的參數進行微調或更新，也不會放寬 token 的接受條件。這確保了生成文本的分布與原始 LLM 完全一致，并且在理論上是可證的。

2. 預備知識

2.1. 推測式采樣

Speculative sampling（Leviathan 等，2023；Chen 等，2023a；Sun 等，2024c；2024b）的核心思想是“先起草，后驗證”：先快速生成一個可能正確的草稿，然后檢查草稿中哪些 token 是可以接受的。我們用 $t_i$ 表示第 i 個 token，用 $T_{a:b}$ 表示從$ t_a$ 到 $t_b$的 token 序列，即 $t_a,t_{a+1},???,t_b$。Speculative sampling 在草稿生成階段與驗證階段之間交替進行。

設有前綴 $T_{1:j}$，在草稿生成階段，speculative sampling 使用一個草稿模型（比原始 LLM 更小的模型）以 $T_{1:j}$ 為前綴，自回歸地生成一個草稿序列 ${\hat{T}}_{j+1:j+k}$，同時記錄每個 token 的概率 $\hat{p}$。

在驗證階段，speculative sampling 調用原始 LLM 來檢查草稿 ${\hat{T}}_{j+1:j+k}$，并記錄其對應的概率 $p$。然后，speculative sampling 從前往后依次決定草稿中每個 token 的接受與否。對于第 $j+i$ 個草稿 token ${\hat{t}}_{j+i}$，它被接受的概率為：$\min (1,p_{j+i}({\hat{t}}_{j+i})/{\hat{p}}_{j+i}({\hat{t}}_{j+i}))$，如果該 token 被接受，則繼續檢查下一個；否則，從分布 $\text{norm}(\max (0,p_{j+i}?{\hat{p}}_{j+i}))$ 中重新采樣一個 token 來替換 ${\hat{t}}_{j+i}$，并丟棄草稿中其后的所有 token。Leviathan 等（2023）在其附錄 A.1 中證明了 speculative sampling 與標準自回歸解碼的分布是一致的。EAGLE 和 EAGLE-2 都遵循這一框架。

2.2 EAGLE

EAGLE（Li 等，2024b）是對 speculative sampling 的一種改進方法。在本工作提交時，EAGLE 在 Spec-Bench（Xia 等，2024）上排名第一。Spec-Bench 是一個為評估不同場景下的 speculative decoding 方法而設計的全面基準測試。

草稿生成階段（Drafting Stage）
與標準的 speculative sampling 使用自回歸方式預測 token 序列不同，EAGLE 在更結構化的特征層級（即在 LM Head 之前的特征層）上進行自回歸生成，然后再使用原始 LLM 的 LM Head 獲取草稿 token。
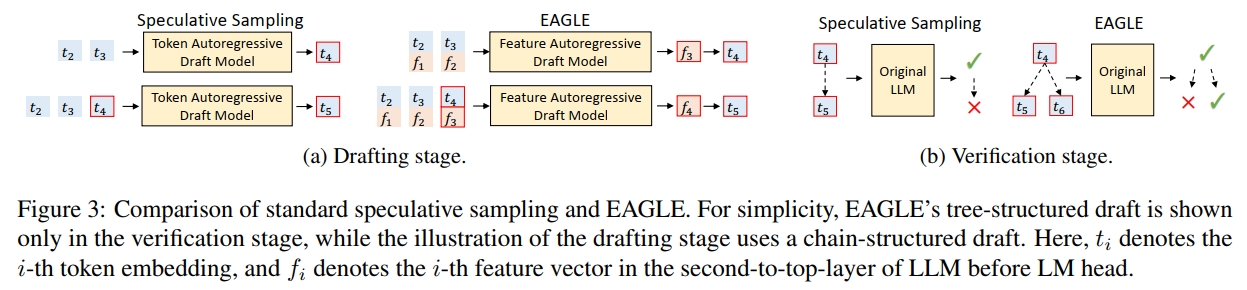
由于該采樣過程會在特征序列中引入不確定性，為了解決這一問題，EAGLE 還向草稿模型輸入一個提前一步的 token 序列，如圖 3a 所示。

驗證階段（Verification Stage）
在標準的 speculative sampling 中，草稿結構是鏈式的（chain-structured），這意味著一旦某個草稿 token 被拒絕，其后所有 token 都必須被丟棄。而 EAGLE 使用樹結構的草稿（tree-structured draft），當某個草稿 token 被拒絕時，可以嘗試其它的備選分支。圖 3b 展示了兩者之間的區別。

EAGLE 與 EAGLE-2 的區別
EAGLE 的草稿樹結構是固定的，在草稿生成階段會填充對應的位置。EAGLE-2 的目標是在此基礎上進一步改進，通過引入可動態調整的草稿樹來增強生成能力。圖 4 以一個簡單的示例說明了 EAGLE 與 EAGLE-2 之間的差異。

3. 觀察結果

3.1 依賴上下文的接受率

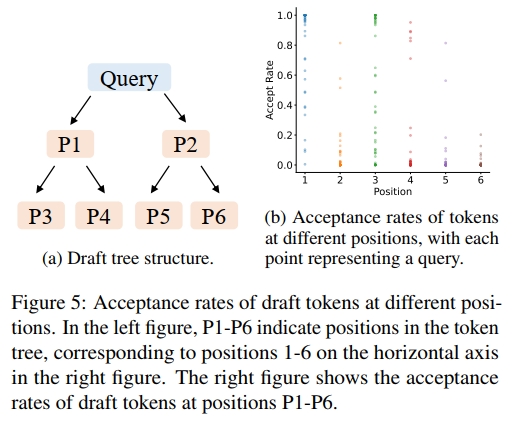
首先，我們評估了使用動態草稿樹的必要性，這取決于草稿token的接受率是否僅與其在草稿樹中的位置相關。我們在 Alpaca 數據集和 Vicuna 7B 模型上測試了不同位置的草稿token的接受率，結果如圖 5 所示。總體來看，草稿token的接受率確實與位置有關：位置 P1 的接受率最高，位置 P6 的接受率最低。草稿樹左上方（如位置 P1）的token接受率較高，而右下方（如位置 P6）的接受率較低。這也解釋了為什么靜態草稿樹（如 EAGLE 和 Medusa 中使用的）在左上方節點較多、右下方節點較少的設計合理性。然而，我們還觀察到相同位置的接受率存在顯著差異，這表明草稿token被接受的概率不僅依賴位置，還與上下文有關。這提示我們，基于上下文的動態草稿樹比靜態草稿樹具有更大的潛力。

3.2 草稿模型的良好校準性

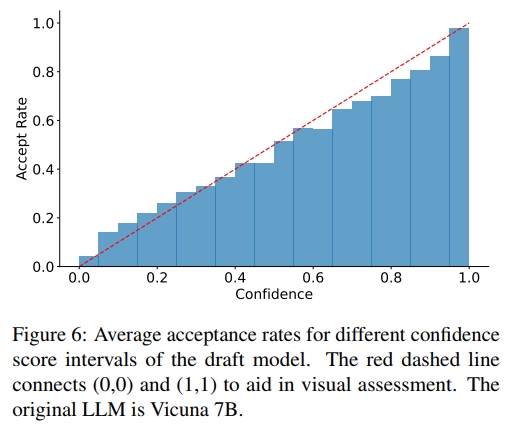
為了應用動態草稿樹，我們需要一種低成本的方法來估計草稿令牌的接受率，而無需調用原始 LLM。我們在 Alpaca 數據集上進行了實驗，探究草稿模型的置信度分數（即 LLM 對每個 token 輸出的概率）與接受率之間的關系。如圖 6 所示，草稿模型的置信度分數與令牌的接受率之間呈現出強正相關關系。例如，置信度分數低于 0.05 的草稿令牌，其接受率約為 0.04；而置信度分數高于 0.95 的令牌，其接受率約為 0.98。因此，我們可以使用草稿模型的置信度分數來估計接受率，無需額外開銷，從而支持對草稿樹的動態調整。在其他方法的草稿模型中，如 GLIDE 和 CAPE（Du 等人，2024），也觀察到了類似的現象。

4. 基于上下文的動態草稿樹

基于上述觀察結果，我們提出 EAGLE-2，這是一種用于 LLM 推理加速的算法，它能夠動態調整草稿樹結構。EAGLE-2 不改變草稿模型的訓練與推理過程，也不影響驗證階段，其改進主要體現在兩個方面：如何擴展草稿樹（見第 4.1 節）以及如何對草稿令牌重新排序（見第 4.2 節）。在擴展階段，我們將當前草稿樹最新一層中最有希望被接受的節點輸入草稿模型，以生成下一層草稿令牌；在重新排序階段，我們選擇接受概率更高的令牌，作為傳入原始 LLM 的驗證輸入。

在草稿樹中，每個節點代表一個 token。下文中，“節點”和“token”將交替使用。

4.1 擴展階段

得益于樹狀注意力機制（tree attention），草稿模型可以同時輸入當前層的所有 token，并在一次前向傳播中計算出下一步 token 的概率，從而實現對當前層所有 token 的擴展。然而，如果一次性輸入太多 token，草稿模型的前向傳播速度可能會下降；同時，草稿樹每一層中的 token 數量會呈指數級增長。因此，我們需要對草稿樹進行選擇性擴展。

我們從當前層中選擇全局接受概率最高的前 $k$ 個 token 進行擴展。在 speculative sampling 中，如果一個草稿 token 被拒絕，則其后所有 token 都會被丟棄；一個 token 只有在其所有前綴都被接受的情況下才最終被接受。因此，token $t_i$ 的全局接受率是從根節點到 $t_i$ 路徑上所有 token 的接受率的乘積。我們將其定義為值 $V_i$：
$$V_i=\prod _{t_j\in \mathrm{Path}(\mathrm{root},t_i)}{p}_j\approx \prod _{t_j\in \mathrm{Path}(\mathrm{root},t_i)}{c}_j,$$
其中，Path(root,?$t_i$) 表示從根節點到草稿樹中節點?$t_i$ 的路徑，$p_j$ 表示節點?$t_j$ 的接受率，$c_j$ 表示草稿模型對?$t? $的置信度分數。第 3.2 節的實驗表明，置信度分數與接受率之間存在顯著的正相關關系。我們利用這一關系來近似估算該值。

從具有較高?V 值的 token 開始的分支更有可能被接受。因此，我們從最后一層中選擇值最大的前?k 個節點作為草稿模型的輸入，并根據其輸出擴展草稿樹。圖 7 頂部展示了擴展階段的流程。

4.2 重排序階段

擴展階段的目的是加深草稿樹。由于接受率的取值范圍在 0 到 1 之間，越深的 token，其值越低。一些未被擴展的淺層節點可能比已擴展的深層節點具有更高的值。因此，我們不會直接將擴展階段選出的 token 作為最終草稿，而是對所有草稿 token 進行重排序，并選擇值最高的前?m?個 token。一個節點的值始終小于或等于其父節點的值。對于值相同的節點，我們優先選擇更淺層的節點。這樣可以確保重排序后選出的前?m?個 token 仍然構成一棵連通的樹。

隨后，我們將這些被選中的 token 展平為一維序列，用作驗證階段的輸入。為了確保與標準自回歸解碼保持一致，還需調整注意力掩碼（attention mask）。在標準自回歸解碼中，每個 token 都可以看到其之前的所有 token，因此形成的是一個下三角的注意力矩陣。而在草稿樹中，來自不同分支的 token 之間不應彼此可見，因此必須根據樹的結構調整注意力掩碼，確保每個 token 只能看到它的祖先節點。圖 7 底部展示了重排序階段的過程。

溫馨提示：
閱讀全文請訪問"AI深語解構" EAGLE-2：通過動態草稿樹加速語言模型推理