目錄
一、前言
二、算法思想
三、代碼實現
四、測試
五、源碼
一、前言
前兩篇學習的Dijkstra算法和Bellman-Ford算法都是用來求解圖的單源最短路徑,即從圖中指定的一個源點出發到圖中其他任意頂點的最短路徑。Dijkstra算法不能求解帶有負權重的圖的最短路徑,而Bellman-Ford算法彌補了這個缺點。本篇文章再來見識一下一個求解多源最短路徑的算法——Floyd-Warshall算法。
多源最短路徑–Floyd-Warshall算法
Floyd-Warshall算法是一種解決多源最短路徑問題(任意兩點間的最短路徑)的算法。
Floyd算法又稱為插點法,是一種利用動態規劃的思想尋找給定的加權圖中多源點之間最短路徑的算法(可以求解帶負權的圖)。 該算法名稱以創始人之一、1978年圖靈獎獲得者、斯坦福大學計算機科學系教授羅伯特·弗洛伊德命名。
我們前面學的Dijkstra算法和Bellman-Ford算法,它們是用來求單源最短路徑的,但是我們如果以所有的頂點為起點都走一遍Dijkstra/Bellman-Ford算法的話,其實也可以得到任意兩點間的最短距離。 不過呢,Dijkstra算法的話不可以求解帶負權路徑的圖,而Bellman-Ford算法呢效率又有點低。 ?
二、算法思想
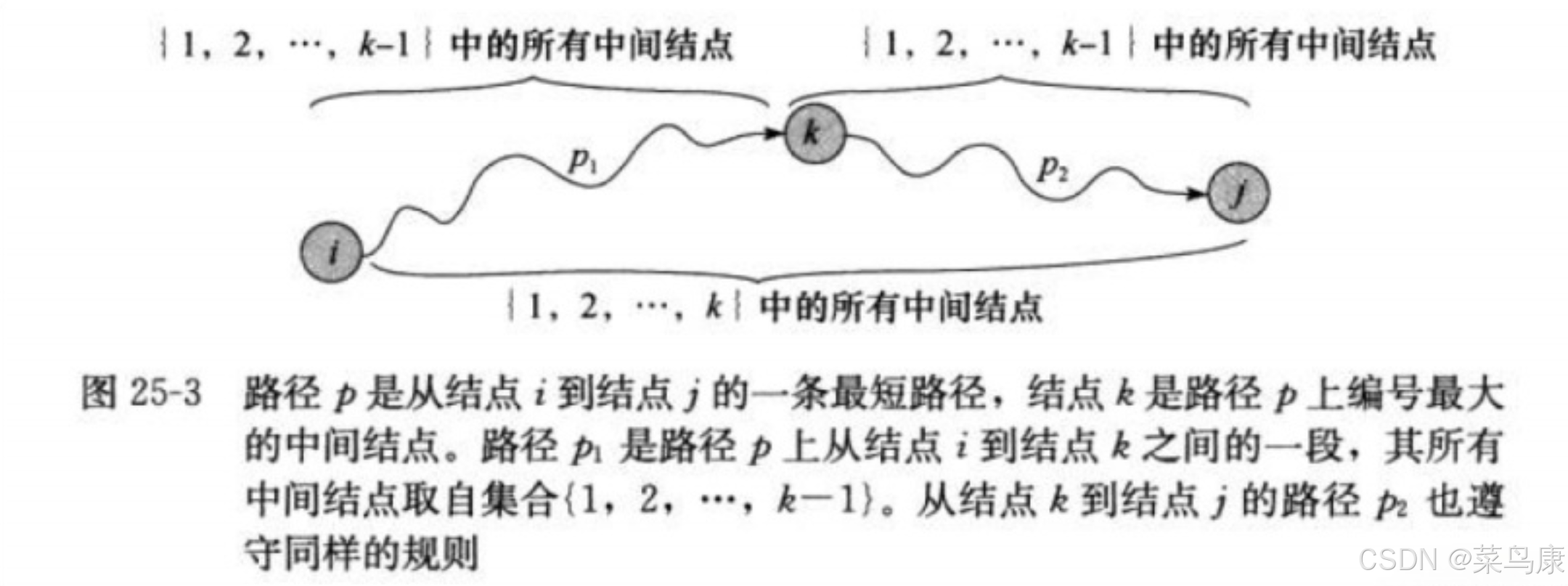
Floyd-Warshall算法考慮的是一條最短路徑的中間節點:
設k是最短路徑p的一個中間節點,那么從i到j的最短路徑p就被分成i到k和k到j的兩段最短路徑p1,p2。 p1是從i到k且中間節點屬于{1,2,…,k-1}取得的一條最短路徑;p2是從k到j且中間節點屬于{1,2,…,k-1}取得的一條最短路徑
 ?如何去求最短路徑p呢?我們先來了解下面的原理
?如何去求最短路徑p呢?我們先來了解下面的原理
 ?即Floyd算法本質是三維動態規劃,D[i][j][k]表示從點i到點j只經過0到k個點最短路徑,然后建立起轉移方程,然后通過空間優化,優化掉最后一維度,變成一個最短路徑的迭代算法,最后即得到所有點的最短路。
?即Floyd算法本質是三維動態規劃,D[i][j][k]表示從點i到點j只經過0到k個點最短路徑,然后建立起轉移方程,然后通過空間優化,優化掉最后一維度,變成一個最短路徑的迭代算法,最后即得到所有點的最短路。
上面原理中的這個公式,在動態規劃中應該叫狀態轉移方程:
Di,j,k表示從i到j的最短路徑,該路徑經過的中間結點是剩余的結點組成的集合中的結點,假設經過k個結點,編號為1…k,然后這里就分為了兩種情況:
- 如果路徑經過了結點k,那么
ij的距離就等于ik的距離加上kj的距離,然后剩余就經過k-1個點- 如果不經過結點k,那
ij的距離就等于i到j經過k-1個點(不包括k)的距離
那i到j的最短路徑就等于這兩種情況中的最小值
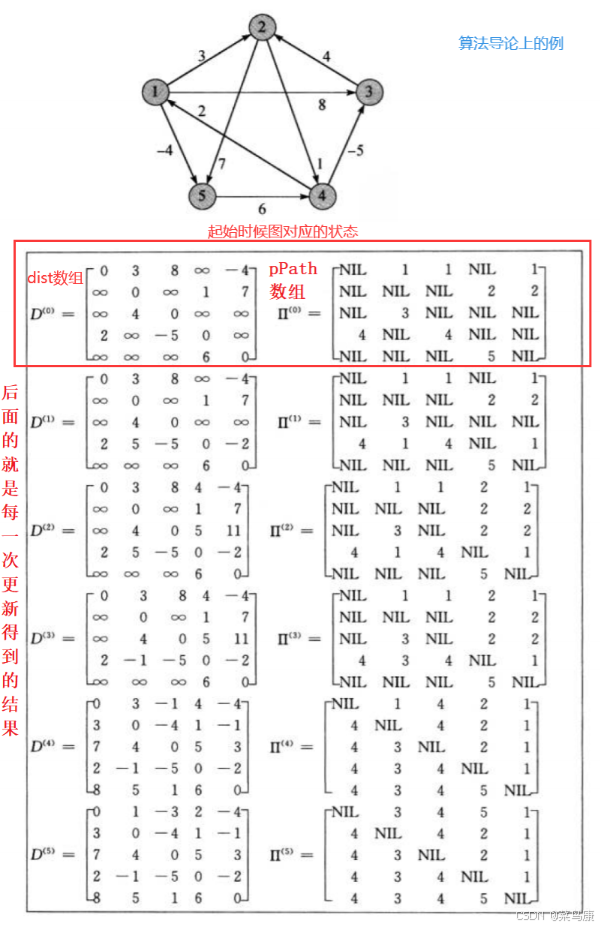
考慮這里如何存儲最短路徑和路徑權重 ?
前面的兩個算法中我們的dist數組和pPath數組都是用了一個一維數組就行了。 但是Floyd-Warshall算法就不一樣了,因為前兩個算法算的是單源最短路徑,而Floyd-Warshall算法是多源最短路徑。 因為前面我們都是一個起點,然后求其它頂點到起點的最短路徑;而現在是多源,即每個頂點都可以是起點,所以我們要記錄每個頂點作為起點時到其它頂點的最短路徑距離和路徑。 那我們就需要用二維數組了。
三、代碼實現
初始化部分
void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)
{size_t n = _vertexs.size(); // 獲取圖中頂點數量vvDist.resize(n); // 調整距離矩陣大小為n*nvvpPath.resize(n); // 調整路徑矩陣大小為n*n// 初始化權值和路徑矩陣
for (size_t i = 0; i < n; ++i) {vvDist[i].resize(n, MAX_W); // 距離初始化為無窮大(MAX_W)vvpPath[i].resize(n, -1); // 路徑初始化為無效值(-1)
}?接著 我們要把圖中所有相連的邊的信息直接更新一下,因為上面我們說了那個公式叫做狀態轉移方程,而這里初始化更新的結果就作為起始狀態,后面通過狀態轉移方程不斷更新得到最終結果

// 直接相連的邊更新
for (size_t i = 0; i < n; ++i) {for (size_t j = 0; j < n; ++j) {if (_matrix[i][j] != MAX_W) { // 存在直接邊vvDist[i][j] = _matrix[i][j]; // 更新直接距離vvpPath[i][j] = i; // 記錄前驅為起點i}if (i == j) { // 對角線處理vvDist[i][j] = W(); // 自身距離設為0(W()生成零值)}}
}?根據狀態轉移方程更新
// 最短路徑更新:i-> {其他頂點} ->j
for (size_t k = 0; k < n; ++k) { // 中間頂點kfor (size_t i = 0; i < n; ++i) { // 起點ifor (size_t j = 0; j < n; ++j) { // 終點j// 嘗試通過k中轉更新路徑
//如果:
//1. ik是相連的
//2. kj是相連的
//3. ik+kj的距離(經過k點)小于ij(不經過k點)的距離,就更新為ik+kj的距離,否則不更新,保存原來不經過k點的距離
//其實就是前面我們給出的狀態轉移方程的判斷(取兩者之間小的那一個)?if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j]) {// 更新最短距離vvDist[i][j] = vvDist[i][k] + vvDist[k][j];// 更新路徑前驅(關鍵步驟!)//注意:這里j的上一個結點不能之間給k,因為k->j路徑上k和j不一定之間相連,//有可能也更新了中間結點(k->...->j),//而kj路徑上的j的上一個是誰?就存儲在vvpPath[k][j]里面vvpPath[i][j] = vvpPath[k][j];}}}四、測試
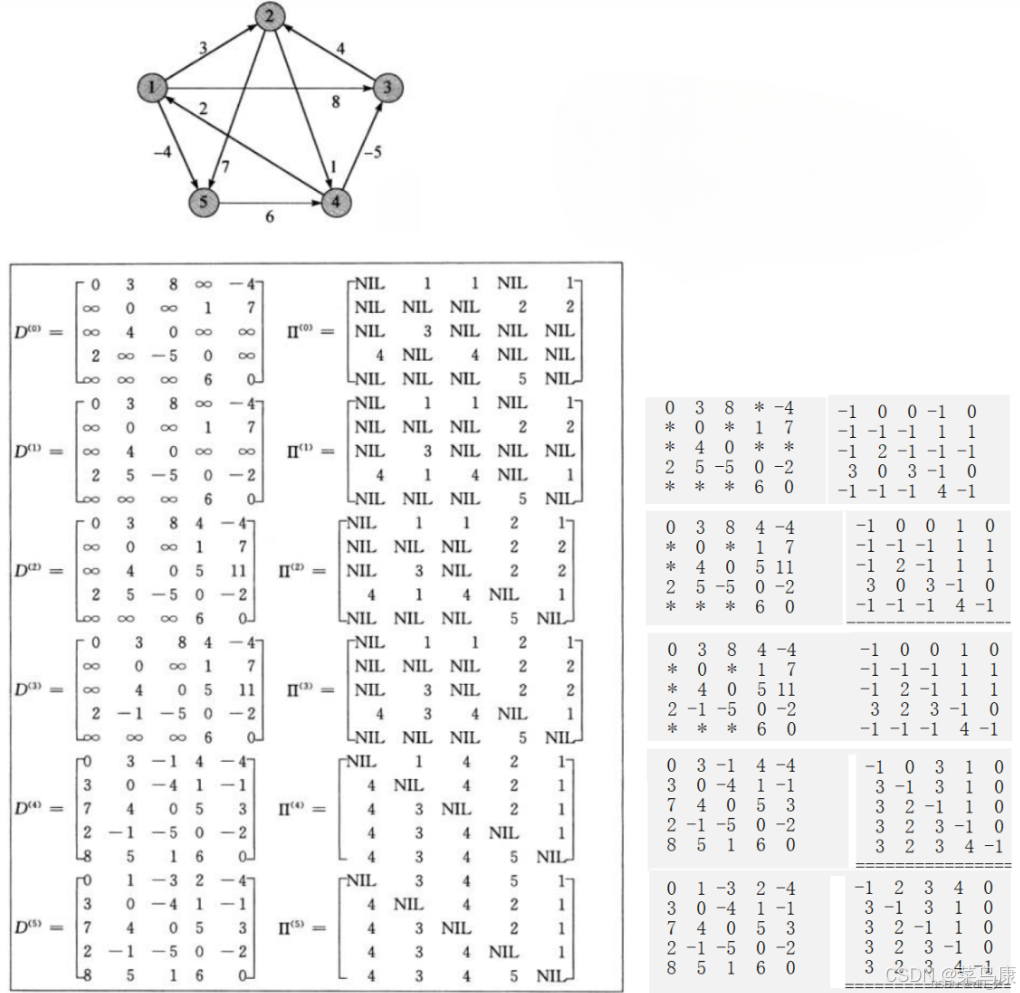
加一個打印權值和路徑的二維數組的代碼,因為上面那個例子也是把每一步對應的兩個二維數組(矩陣)畫了出來,我們可以打印(每個頂點作為中間結點更新之后的都打印一下)出來觀察對比一下:
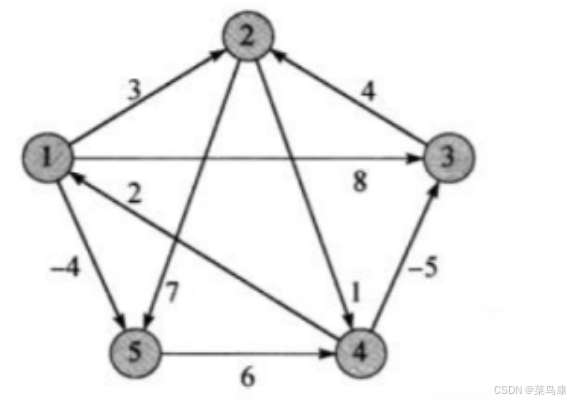
// 打印權值和路徑矩陣觀察數據for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (vvDist[i][j] == MAX_W){//cout << "*" << " ";printf("%3c", '*');}else{//cout << vvDist[i][j] << " ";printf("%3d", vvDist[i][j]);}}cout << endl;}cout << endl;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){//cout << vvParentPath[i][j] << " ";printf("%3d", vvpPath[i][j]);}cout << endl;}cout << "=================================" << endl;void TestFloydWarShall(){const char* str = "12345";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('1', '2', 3);g.AddEdge('1', '3', 8);g.AddEdge('1', '5', -4);g.AddEdge('2', '4', 1);g.AddEdge('2', '5', 7);g.AddEdge('3', '2', 4);g.AddEdge('4', '1', 2);g.AddEdge('4', '3', -5);g.AddEdge('5', '4', 6);vector<vector<int>> vvDist;vector<vector<int>> vvParentPath;g.FloydWarshall(vvDist, vvParentPath);}還是使用上面的圖解中的圖
運行結果
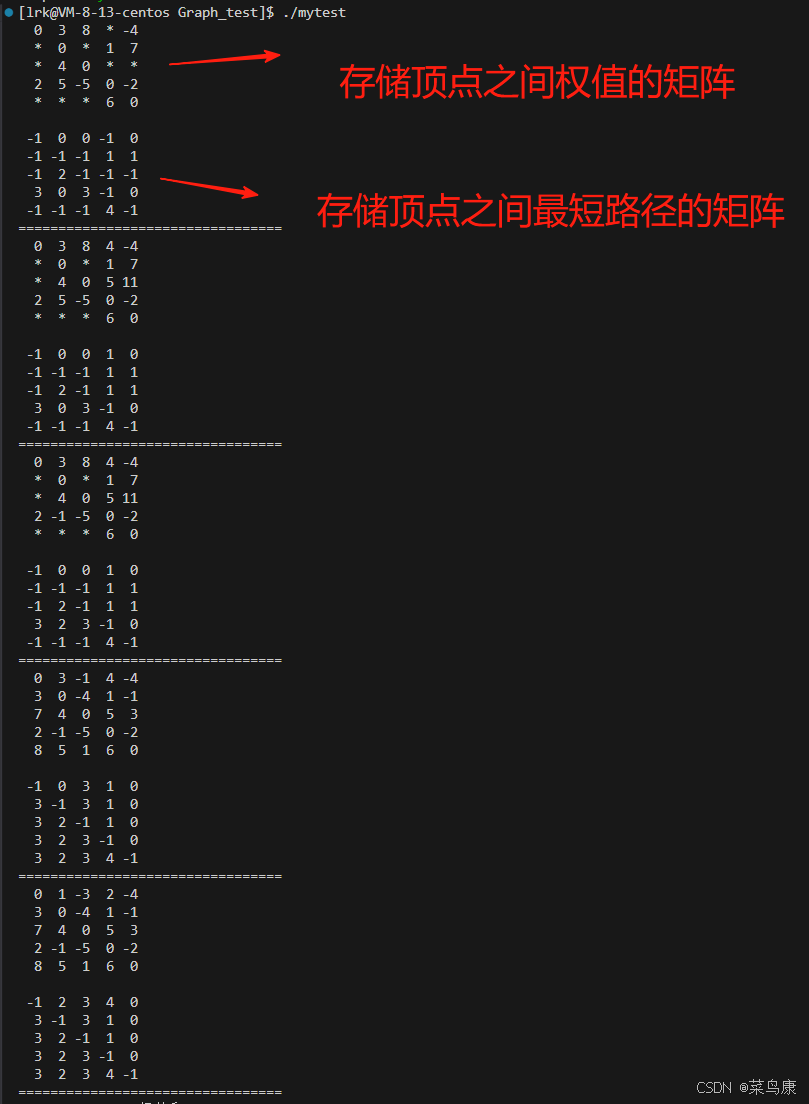
為了方便對比
?∞等價于*? ? NIL等價于-1
另外pPath數組例子中給的直接就是結點本身(他這里的頂點就是1 2 3 4 5),我們用的是頂點映射的下標,所以大家看到比他的值小1
接著我們打印一下任意兩個頂點之間的最短路徑
// 打印任意兩點之間的最短路徑for (size_t i = 0; i < strlen(str); ++i){g.PrintShortPath(str[i], vvDist[i], vvParentPath[i]);cout << endl;}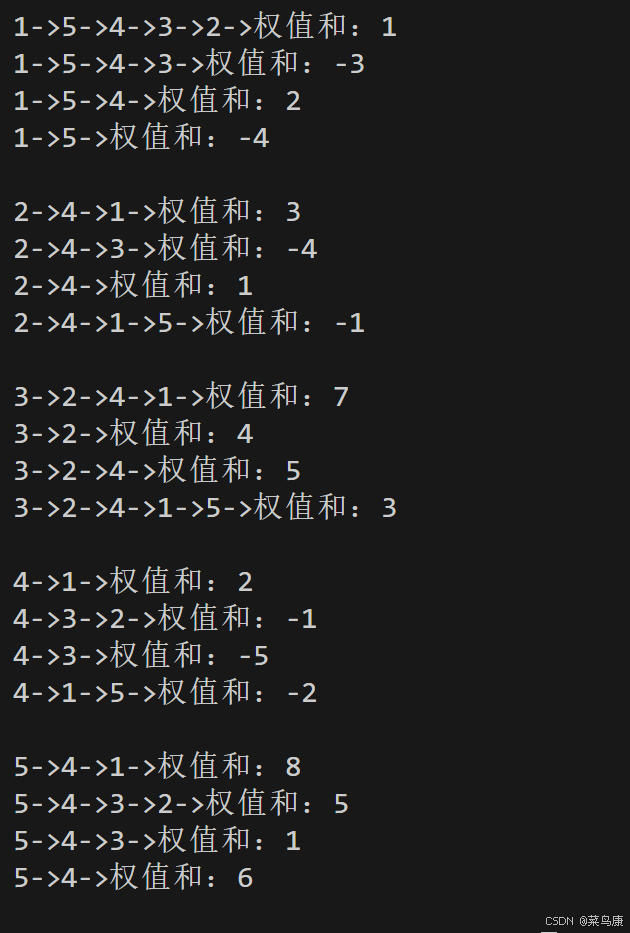
五、源碼
void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath){size_t n = _vertexs.size();vvDist.resize(n);vvpPath.resize(n);// 初始化權值和路徑矩陣for (size_t i = 0; i < n; ++i){vvDist[i].resize(n, MAX_W);vvpPath[i].resize(n, -1);}// 直接相連的邊更新一下for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (_matrix[i][j] != MAX_W){vvDist[i][j] = _matrix[i][j];vvpPath[i][j] = i;}if (i == j){vvDist[i][j] = W();}}}// abcdef a {} f || b {} c// 最短路徑的更新i-> {其他頂點} ->jfor (size_t k = 0; k < n; ++k){for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){// k 作為的中間點嘗試去更新i->j的路徑if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j]){vvDist[i][j] = vvDist[i][k] + vvDist[k][j];// 找跟j相連的上一個鄰接頂點// 如果k->j 直接相連,上一個點就k,vvpPath[k][j]存就是k// 如果k->j 沒有直接相連,k->...->x->j,vvpPath[k][j]存就是xvvpPath[i][j] = vvpPath[k][j];}}}// 打印權值和路徑矩陣觀察數據for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (vvDist[i][j] == MAX_W){//cout << "*" << " ";printf("%3c", '*');}else{//cout << vvDist[i][j] << " ";printf("%3d", vvDist[i][j]);}}cout << endl;}cout << endl;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){//cout << vvParentPath[i][j] << " ";printf("%3d", vvpPath[i][j]);}cout << endl;}cout << "=================================" << endl;} }感謝閱讀!
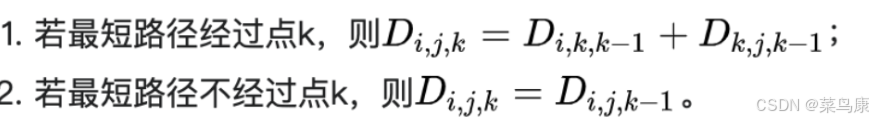
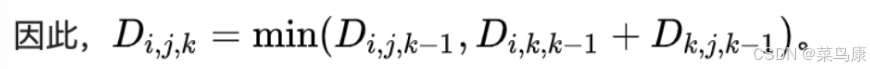
 打不開,無網絡連接的問題!)






 視頻教程 - 詞云圖-微博評論詞云圖實現)

、內核鏈表、棧(系統棧、實現方式)、隊列(實現方式、應用))
:windows安裝使用node.js 安裝express,suquelize,sqlite,nodemon)

![[Python 基礎課程]猜數字游戲](http://pic.xiahunao.cn/[Python 基礎課程]猜數字游戲)


)



)