---

理解 LogisticRegression 的核心參數：以約會數據集為例

邏輯回歸（Logistic Regression）是機器學習中一種基礎且重要的分類算法，特別適用于解決二分類和多分類問題。本文將基于 sklearn.linear_model.LogisticRegression 的用法，結合一個典型的約會數據集，通過代碼實踐，詳解其核心參數的作用與調優技巧。

下方鏈接下載文件

作者《機器學習實戰》 Peter Harrington 的配套代碼

machinelearninginaction/Ch02/datingTestSet2.txt at master · pbharrin/machinelearninginactionhttps://github.com/pbharrin/machinelearninginaction/blob/master/Ch02/datingTestSet2.txt（完整代碼在底部）

一、模型背景與代碼示例

我們使用《機器學習實戰》中的數據集 datingTestSet2.txt

其數據包含三列特征和一個表示喜歡程度的標簽（1：不喜歡，2：魅力一般，3：非常喜歡）。

通過如下代碼訓練邏輯回歸模型：

from sklearn.linear_model import LogisticRegression# 初始化邏輯回歸模型
model = LogisticRegression()
model.fit(X_train, y_train)

接下來我們圍繞 LogisticRegression 的主要參數逐個進行解析。

---

二、核心參數詳解

1?? C: 正則化強度的倒數（默認值：1.0）

• 含義：控制正則化項的權重。較小的 C 值表示更強的正則化，會限制模型復雜度，有助于防止過擬合。

• 實例：在本文代碼中使用了 C=0.01，代表較強的正則化。

model = LogisticRegression(C=0.01)

? 建議：

• 若模型過擬合（訓練集準確高，測試集低）→ 減小 C

• 若模型欠擬合（整體準確率都低）→ 增大 C

---

2?? penalty: 正則化方式（默認值：'l2'）

• 可選值：'l1', 'l2', 'elasticnet', 'none'

• 'l1'：可產生稀疏模型（特征選擇）

• 'l2'：默認值，更適合大多數線性問題

• 'elasticnet'：結合 l1 與 l2

• 'none'：不使用正則化（風險較大）

model = LogisticRegression(penalty='l2')

? 注意：不同 solver 對支持的 penalty 有限制，例如 'liblinear' 支持 'l1' 和 'l2'，而 'saga' 才支持 'elasticnet'。

---

3?? solver: 優化算法（默認值：'lbfgs'）

• 可選值：

  • 'liblinear'：適用于小數據集，支持 'l1' 與 'l2'

  • 'lbfgs'：適合多分類（支持 'l2'），速度快，默認值

  • 'newton-cg'、'sag'、'saga'：適合大數據

model = LogisticRegression(solver='lbfgs')

? 實際建議：

• 小數據集（如本文案例） → liblinear

• 多分類任務 → lbfgs 或 saga

• 稀疏特征（如文本） → saga

---

4?? multi_class: 多分類策略（默認：'auto'）

• 'ovr'（一對其余，One-vs-Rest）：訓練多個二分類器，速度快，解釋性強

• 'multinomial'：直接優化多分類損失函數，預測效果通常更優

• 'auto'：自動選擇（liblinear → ovr，其他 → multinomial）

model = LogisticRegression(multi_class='multinomial')

---

5?? max_iter: 最大迭代次數（默認值：100）

• 當模型無法收斂時，可以調大該值，如設置為 1000。

• 若出現如下報錯：ConvergenceWarning: lbfgs failed to converge → 增大 max_iter

model = LogisticRegression(max_iter=1000)

---

6?? class_weight: 類別權重（默認值：None）

• 用于處理類別不平衡問題，如設為 'balanced' 會自動按樣本數調整權重

• 或自定義字典，例如 {1:1, 2:2, 3:3}

model = LogisticRegression(class_weight='balanced')

---

7?? random_state: 隨機種子（可重復結果）

• 設置后模型行為可復現，例如 random_state=42

• 在劃分訓練/測試集、優化器初始化中有用

model = LogisticRegression(random_state=42)

除了LogisticRegression的參數，還有：

train_test_split的參數：

參數名	類型	說明
X, y	數組或矩陣	特征矩陣 X 和標簽向量 y，支持 NumPy、Pandas、List 等
test_size	float 或 int	測試集占比（如 0.25）或測試集樣本數（如 100）
train_size	float 或 int	訓練集占比或樣本數，默認自動補足（1 - test_size）
random_state	int	隨機種子，用于保證劃分可復現。設為固定值（如 42）結果不會變
shuffle	bool	是否在劃分前打亂數據（默認 True，一般都要打亂）
stratify	array-like 或 None	分層抽樣依據（常設為 y），用于保持標簽比例一致（分類任務推薦）

---

三、系數和截距

print(model.coef_)       # 每個類別的特征系數（權重）
print(model.intercept_)  # 每個類別的偏置（截距）

對于三分類模型（標簽為 1、2、3），會輸出三組線性決策函數（即分割面）：

y = w1*x1 + w2*x2 + w3*x3 + b

如輸出結果如下：

分割線1: y = -0.1234x1 + 0.2345x2 - 0.5678x3 + 1.2345
分割線2: y = ...

---

四、總結：調參建議

問題	建議參數
模型過擬合	減小 C，增加正則化強度
模型欠擬合	增大 C，嘗試 multinomial
類別不平衡	使用 class_weight='balanced'
收斂慢或警告	增加 max_iter，或更換 solver
特征太多，想降維	使用 penalty='l1', solver='liblinear'

---

附：完整模型構建代碼

import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_splitdata = np.loadtxt('datingTestSet2.txt')
X = data[:, :-1]
y = data[:, -1]# 劃分訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=100)# 訓練邏輯回歸模型
model = LogisticRegression(C=0.01, max_iter=200, multi_class='auto', solver='lbfgs')
model.fit(X_train, y_train)print("訓練集準確率：", model.score(X_train, y_train))
print("測試集準確率：", model.score(X_test, y_test))
print("權重系數：", model.coef_)
print("截距：", model.intercept_)# 自變量系數和截距
a = model.coef_
b = model.intercept_
print(f"分割線1:y = {a[0][0]:.4f}x1 + {a[0][1]:.4f}x2 + {a[0][2]:.4f}x3 + {b[0]:.4f}")
print(f"分割線2:y = {a[1][0]:.4f}x1 + {a[1][1]:.4f}x2 + {a[1][2]:.4f}x3 + {b[1]:.4f}")
print(f"分割線3:y = {a[2][0]:.4f}x1 + {a[2][1]:.4f}x2 + {a[2][2]:.4f}x3 + {b[2]:.4f}")

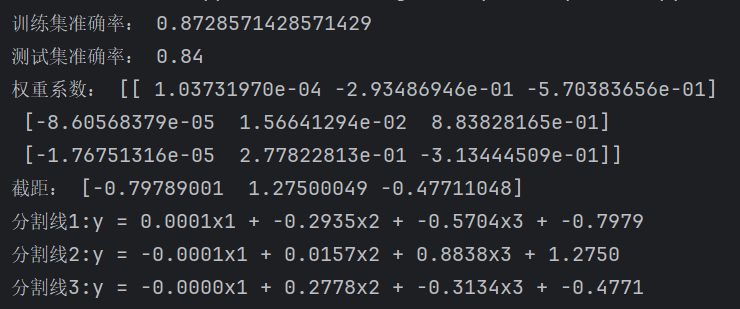
分割線中的系數四舍五入了。