目錄

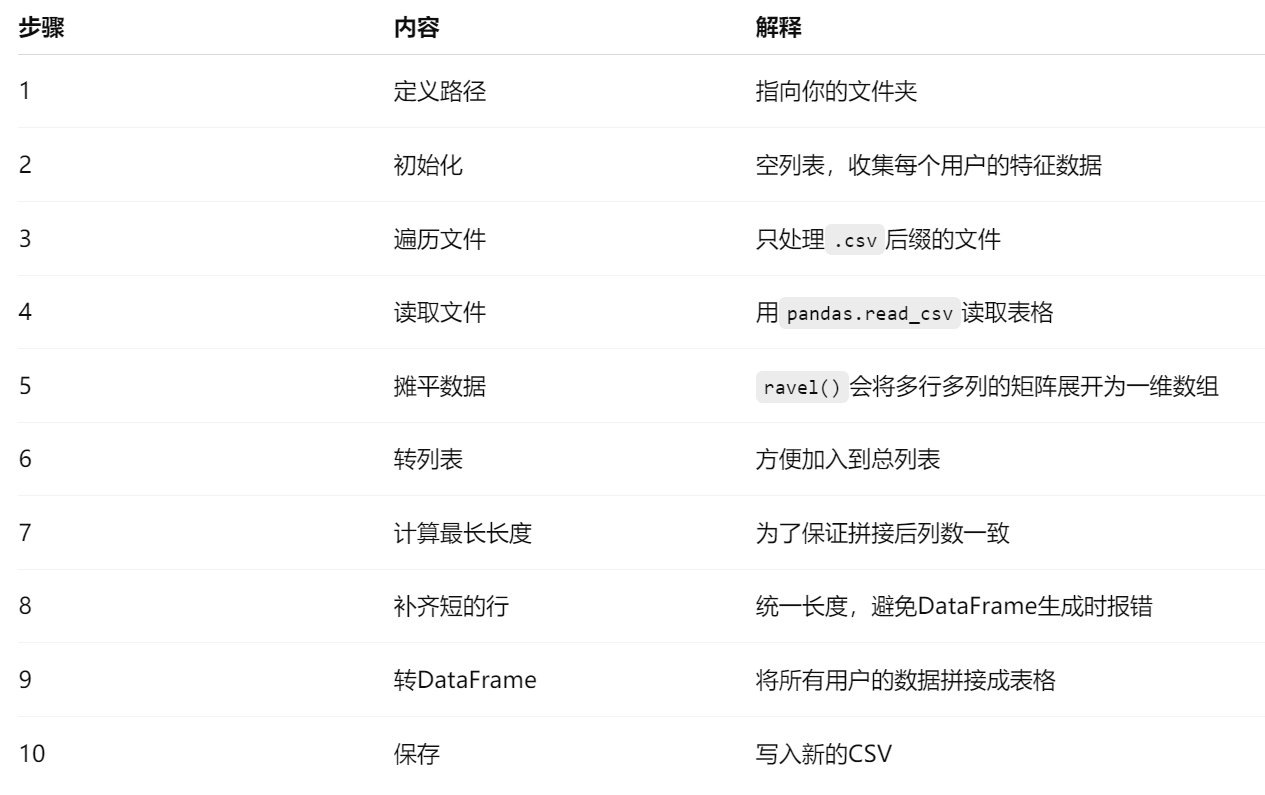
具體做法

可視化方法1：PCA降維

可視化方法2、TSNE降維可視化（非線性降維，更適合聚類）

可視化方法3、輪廓系數評判好壞

---

每個文件有很多行列的信息，每列是一個駕駛相關的數據，需要對這些文件進行聚類，每個文件代表一個用戶的行為。

目標：聚類效果好，將各個用戶行為分開。

具體做法

數據預處理

①將每個文件攤平到一行，匯總成為一個很多用戶（文件）組成的csv文件。

import os
import pandas as pd# 1. 定義目標文件夾路徑
folder_path = "/home/zqy/A_paper/diff_time_norm/cleantime"# 2. 用于存放每個文件（用戶）攤平后的數據
flattened_data = []# 3. 遍歷文件夾下所有CSV文件
for filename in os.listdir(folder_path):if filename.endswith("truncated.csv"):file_path = os.path.join(folder_path, filename)# 4. 讀取CSV文件df = pd.read_csv(file_path)# 5. 將整個DataFrame按行攤平成一維（每行數據拼在一起）# df.values：轉為numpy數組，ravel(): 展平flattened_row = df.values.ravel()# 6. 轉成List（確保可以加入到匯總列表）flattened_data.append(flattened_row.tolist())# 7. 找到最長的一行長度，補齊其他行
max_length = max(len(row) for row in flattened_data)# 8. 確保所有行都補齊（空位補None或0）
flattened_data_padded = [row + [None] * (max_length - len(row)) for row in flattened_data]# 9. 將所有行轉換成DataFrame
summary_df = pd.DataFrame(flattened_data_padded)# 10. 保存到新CSV文件
summary_df.to_csv("/home/zqy/A_paper/diff_time_norm/cleantime/flattened_summary.csv", index=False)print("匯總文件已生成。")

“DataFrame”是Python中pandas庫的一個核心數據結構，它類似于Excel中的表格，是一個二維的、大小可變的、異構的數據結構。它由行和列組成，每一列可以存儲不同類型的值，比如整數、浮點數、字符串等。在你提到的上下文中，它指的是包含有“數值型”數據的列的表格。

②對匯總后的文件的每一行當中有列表形式的展開處理（因為聚類要求每一列的元素都是數值）

#把多元組的列表轉化為多個列import pandas as pd
import astdef expand_list_columns(df):new_cols = []for col in df.columns:if df[col].apply(lambda x: isinstance(x, str) and x.startswith('[') and x.endswith(']')).any():# 將字符串轉為列表expanded = df[col].apply(lambda x: ast.literal_eval(x) if isinstance(x, str) else [])max_len = expanded.map(len).max()for i in range(max_len):df[f'{col}_{i}'] = expanded.map(lambda x: x[i] if i < len(x) else None)new_cols.append(col)# 刪除原始的列表列df = df.drop(columns=new_cols)return df# 讀取CSV
df = pd.read_csv('/home/zqy/A_paper/diff_time_norm/cleantime/flattened_summary.csv')# 轉換
df_expanded = expand_list_columns(df)# 保存
df_expanded.to_csv('/home/zqy/A_paper/diff_time_norm/cleantime/expanded_features.csv', index=False)

③使用kmeans進行聚類處理。

import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt# 1. 讀取數據
data_path = "/home/zqy/A_paper/diff_time_norm/cleantime/expanded_features.csv"
df = pd.read_csv(data_path)# 2. 數據預處理（空缺值補0，或用均值/中位數填充）
df_filled = df.fillna(0)  # 或 df.fillna(df.mean())# 3. 聚類，這里以KMeans為例，設定聚類數量k
k = 6  # 你可以根據需求調整
kmeans = KMeans(n_clusters=k, random_state=42)
# print(df_filled.dtypes)df_filled = df_filled.fillna(0)clusters = kmeans.fit_predict(df_filled)# 將聚類結果添加回DataFrame
df_filled['cluster'] = clusters# 4. 使用PCA降維到2D便于可視化
pca = PCA(n_components=2)
reduced_data = pca.fit_transform(df_filled.drop('cluster', axis=1))# 5. 可視化
plt.figure(figsize=(8,6))
scatter = plt.scatter(reduced_data[:, 0], reduced_data[:, 1], c=clusters, cmap='viridis', s=50)
plt.title('Clustering Visualization with PCA')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.colorbar(scatter, label='Cluster')
plt.grid(True)
plt.show()

可視化方法1：PCA降維

????????缺點是只有二維，看不清楚聚類的邊界。

pca = PCA(n_components=2)
reduced_data = pca.fit_transform(df_filled.drop('cluster', axis=1))plt.figure(figsize=(8,6))
scatter = plt.scatter(reduced_data[:, 0], reduced_data[:, 1], c=clusters, cmap='viridis', s=50)
plt.title('Clustering Visualization with PCA')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.colorbar(scatter, label='Cluster')
plt.grid(True)
plt.show()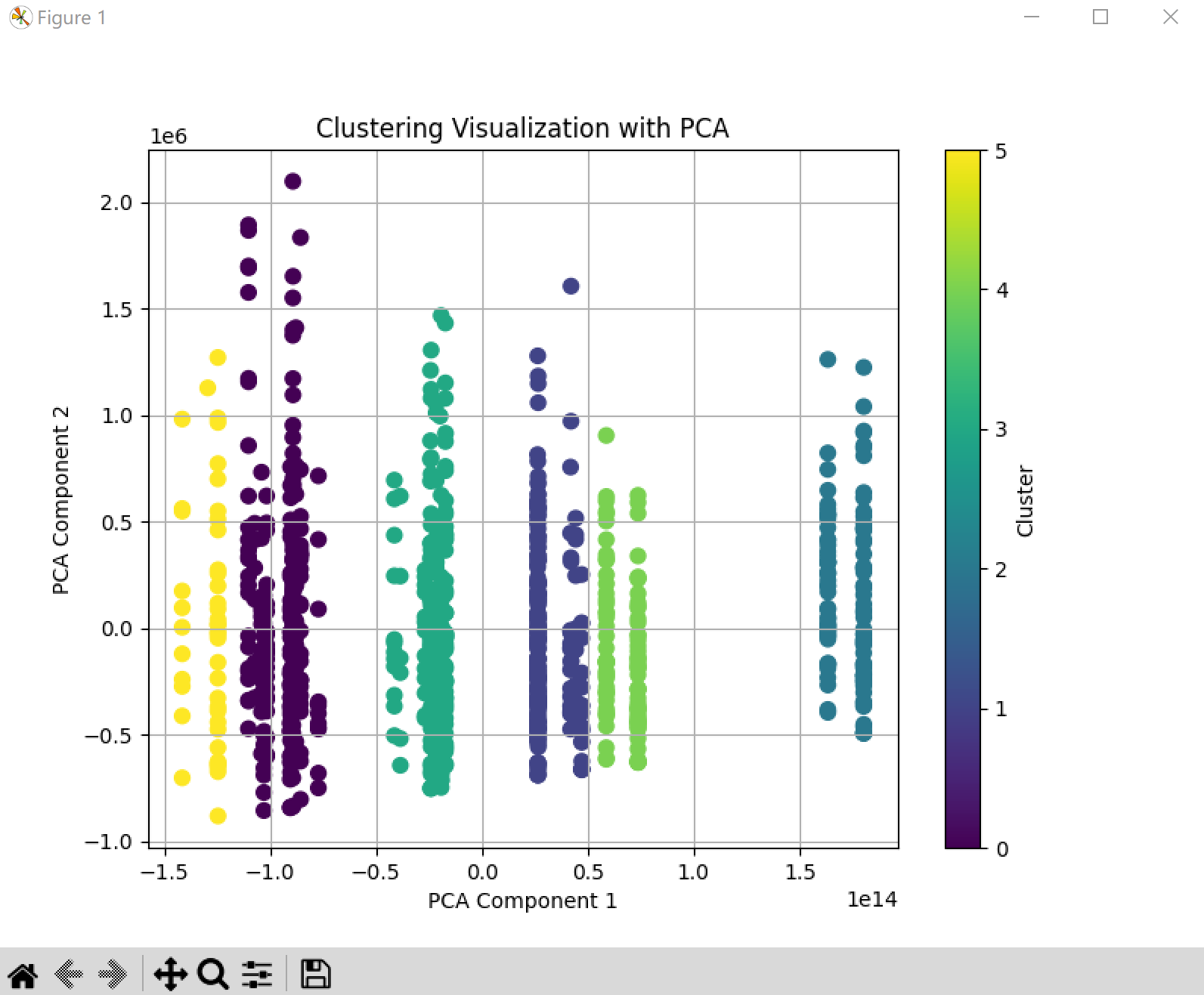

這個圖是PCA將維度降低來可視化的方法。

可視化方法2、TSNE降維可視化（非線性降維，更適合聚類）

from sklearn.manifold import TSNEtsne = TSNE(n_components=2, random_state=42, perplexity=30)
tsne_result = tsne.fit_transform(df_filled.drop('cluster', axis=1))plt.figure(figsize=(8,6))
plt.scatter(tsne_result[:,0], tsne_result[:,1], c=clusters, cmap='viridis', s=50)
plt.title('Clustering Visualization with t-SNE')
plt.xlabel('t-SNE Component 1')
plt.ylabel('t-SNE Component 2')
plt.colorbar(label='Cluster')
plt.grid(True)
plt.show()

TSNE 更適合看復雜的、非線性的數據分布。

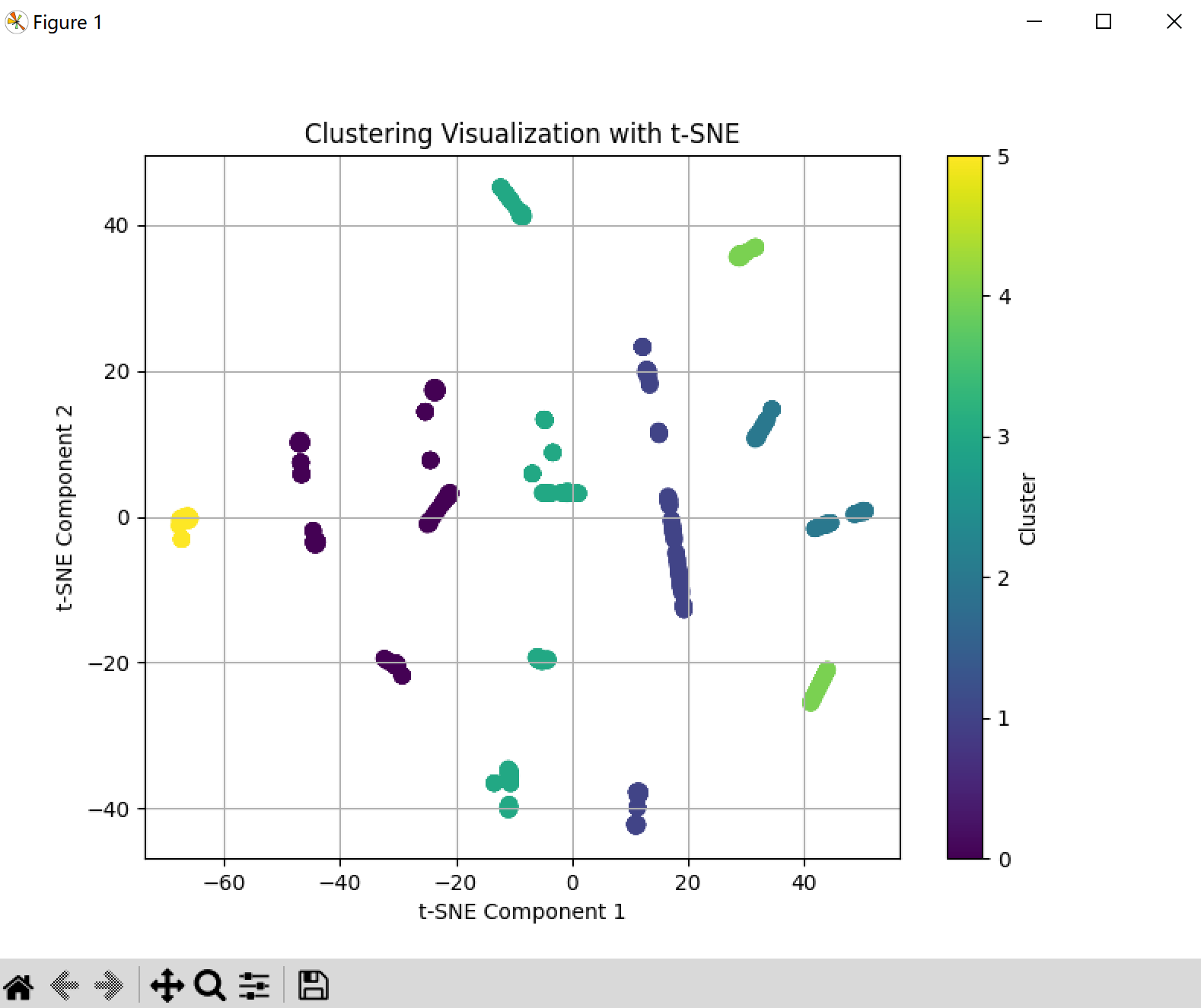
可視化方法3、輪廓系數評判好壞

from sklearn.metrics import silhouette_scorescore = silhouette_score(df_filled.drop('cluster', axis=1), clusters)
print(f'Silhouette Score: {score}')

結論解釋：

• 分數在 -1 ~ 1 之間

• 接近 1：聚類好，簇內緊湊、簇間分離

• 接近 0：聚類一般

• 接近 -1：聚類效果差

缺點：目前沒有考慮不同列數據之間是否有相關性，沒有把時間信息充分考慮進來，而是分開每列聚類。并且utime也進行聚類導致效果較好但是不加入效果不夠好。

——小狗照亮每一天

20250722