ABQ-LLM：用于大語言模型的任意比特量化推理加速

溫馨提示：
本篇文章已同步至"AI專題精講" ABQ-LLM：用于大語言模型的任意比特量化推理加速

摘要

大語言模型（LLMs）在自然語言處理任務中取得了革命性的進展。然而，其實際應用受到巨大的內存與計算開銷的限制。訓練后量化（Post-Training Quantization，PTQ）被認為是一種有效的LLM推理加速方法。盡管PTQ在LLM模型壓縮中越來越受歡迎，但其部署仍面臨兩大挑戰：

首先，低比特量化會導致性能下降；其次，受限于GPU中整數計算單元類型的限制，不同精度下的量化矩陣運算無法被有效加速。

為了解決這些問題，我們提出了一種新穎的任意比特量化算法與推理框架 —— ABQ-LLM（Arbitrary-Bit Quantized LLM）。它不僅在各種量化設置下實現了更優的性能，還支持在GPU上進行高效的任意精度量化推理。

ABQ-LLM 引入了以下幾個關鍵創新：

分布校正方法：針對Transformer模塊中的權重和激活值全量化所引起的分布偏移問題，提出校正方法以提升低比特精度下的性能；
比特平衡策略（Bit Balance Strategy）：用于緩解在極低比特（如2-bit）下由于分布不對稱帶來的性能退化；
創新的量化加速框架：基于 BTC（二進制TensorCore）等價操作，重新構建任意精度組合下的量化矩陣乘法，不再依賴于INT4/INT8計算單元，從而使每個組件的比特寬度收益都能轉化為實際的加速收益，并在混合精度設置下最大化性能（如W6A6、W2A8）。

在LLaMA-7B模型的W2*A8量化配置下，ABQ-LLM在WikiText2數據集上取得了 7.59的困惑度（相比AffineQuant的9.76降低了2.17）。與SmoothQuant相比，ABQ-LLM實現了 1.6倍的推理加速和 2.7倍的顯存壓縮率。

1 引言

近年來的大語言模型（LLMs）（如 Bubeck et al., 2023；Touvron et al., 2023a,b）在多個自然語言任務上展現了驚人的能力，包括推理（Clark et al., 2019, 2018）、認知處理（Xu et al., 2023a；Hardy et al., 2023）和對話生成（Hu et al., 2023）。然而，這些模型普遍擁有龐大的參數規模，帶來了極高的顯存占用與帶寬瓶頸（Zheng et al., 2024；Kim et al., 2023）。

訓練后量化（PTQ） 是一種能夠顯著減少計算與存儲開銷的有效手段。該技術通過將LLMs中的權重與激活值從高精度浮點數轉換為低精度整數進行存儲，并在推理過程中使用高效的整數矩陣乘法算子，從而加速模型推理。

目前，LLMs 中約 80% 的計算與參數訪問 都集中在 通用矩陣乘法（GEMM） 和 向量乘法（GEMV） 操作上。尤其在自回歸解碼階段，GEMM操作基本退化為GEMV（因為是逐token生成），因此GEMV的計算效率和內存訪問效率直接決定了LLM推理的速度與能耗。

為了提升GEMM/GEMV的內存訪問效率，LLM推理中通常采用量化推理策略。目前主流方法是僅對權重量化，即內核基于反量化后的FP16值進行計算。然而在高并發場景下，這種方法的性能提升十分有限。

為了進一步增強量化推理的性能，業界開始推進權重與激活值的全量化（WA全量化），以減少激活內存訪問并充分利用GPU上的量化核算能力（如NVIDIA提供的量化核）。但目前該領域的實際應用仍存在多項挑戰：

NVIDIA僅支持有限數量的硬件加速指令（Lin et al., 2024a；Ashkboos et al., 2024；Zhao et al., 2024），限制了量化算法的設計空間；
非主流組合（如W4A8、W2A4）需要在計算過程中轉換為W8A8或W4A4，從而降低效率（Lin et al., 2024b）；
由于GEMV操作的存在，在batch size小于8時需進行額外padding，導致W4A4與W8A8量化在小batch推理下效率低下；
最后，在極低比特（如W2A8、W2A6）下，WA全量化模型在精度上仍面臨較大挑戰。

ABQ-LLM 針對上述挑戰提出解決方案，在保持精度的同時，實現了真正意義上的任意比特量化推理加速。

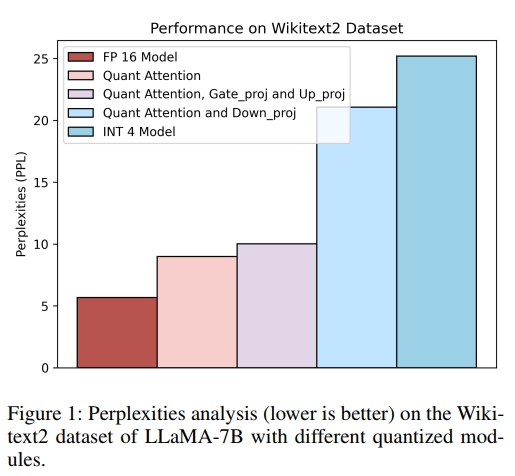
在這里插入圖片描述

在本文中，我們提出了一種面向訓練后量化（Post-Training Quantization, PTQ）的新型量化框架，稱為 ABQ-LLM。通過分析transformer模塊內部各組成部分的量化敏感性（見圖1）以及量化前后的注意力圖變化（見圖2），我們發現 down proj線性層和注意力圖（attention map）對量化特別敏感。

為此，我們提出了以下兩項關鍵技術：

雙余弦相似度分布校正（double cosine similarity distribution correction）；
注意力圖分布自舉（attention map distribution bootstrap），

以對down proj的輸出進行校正，從而精確調整量化常數，恢復在低比特（如 W6A6、W4A4 和 W2A8）下的模型性能。

此外，我們還對低比特量化下的性能下降進行了深入分析，并通過提出比特平衡策略（bit balance strategy），解決了諸如INT2這類低比特表示中常見的不對稱損失問題（asymmetric loss），顯著提升了INT2配置下的量化性能。

最后，我們實現了一款基于BTC（二進制TensorCore）等價計算的定制化軟件引擎，首次在LLM領域實現了真正意義上的量化自由（quantization freedom）。該引擎：

擺脫了INT4/INT8計算單元的限制；
有效規避了GEMV計算瓶頸；
在LLaMA-7B的W2A8配置下，相較于SmoothQuant實現了1.6倍的最終推理加速，并達到了SOTA級別的性能表現。

我們的貢獻如下：

我們提出了一種新穎的塊級分布校正與補償方案，用于緩解因權重與激活值全量化所引起的分布偏移，從而顯著提升低比特下的模型性能；
我們解決了INT2等低比特量化中的不對稱損失問題，通過比特平衡策略顯著改善了INT2配置下的量化效果，提升了模型在極低比特精度下的表現；
我們設計并實現了首個在LLM領域實現量化自由的軟件引擎，打破了INT4/INT8算力限制，有效規避GEMV性能瓶頸。在LLaMA-7B的W2A8配置下，相較于SmoothQuant實現了1.6倍的加速效果，達到當前最優性能。

在這里插入圖片描述

2 相關工作

大語言模型（LLM）的量化可以大致分為兩類：僅對權重進行量化，以及同時對權重和激活值進行量化。

權重量化。 為了緩解計算負擔，一些研究聚焦于僅對權重進行量化。已有方法通過保留關鍵通道實現精確的8比特量化。也有方法利用基于Hessian的誤差補償，降低LLM中的量化誤差，從而實現3比特量化。另有研究考慮激活值中離群點對權重量化的影響，顯著提升了量化模型的性能。部分方法通過可學習的碼本或引入額外微調，推動了2比特量化的可行性。還有研究通過非結構化的混合精度細粒度權重分組，提升了后訓練量化的表現。此外，也有一系列工作采用高效的參數高效微調技術，通過微調進一步壓縮模型權重。

權重-激活量化。 與僅對權重進行量化不同，權重-激活量化在加速LLM推理的過程中，同時對權重和激活值（包括KV緩存）進行量化。這類方法的主要挑戰在于處理激活值中的離群點，這些離群點可能導致嚴重的量化誤差。為了解決這一問題，已有工作提出了細粒度、硬件友好的全量化方案，對權重和激活值進行處理。還有方法通過數學等效變換，將量化難點從激活值轉移到權重，從而實現8比特的權重與激活值聯合量化。一些方法則通過訓練量化參數進一步增強模型性能。然而受限于GPU平臺的指令集限制，盡管某些工作實現了更低比特數的量化（例如6比特），實際推理時仍只能使用8比特的計算單元。此外，即便是實現了低比特量化，這些方法依然難以在推理階段擺脫硬件限制，無法充分發揮潛力。

在這里插入圖片描述

3 方法

本節將詳細介紹我們提出的 ABQ-LLM 方法。我們首先描述分布校正與比特平衡策略，然后介紹任意比特精度的推理框架。

3.1 預備知識

已有研究通過縮放激活值中的離群點來實現權重-激活全量化，但這會增加權重數值范圍的變化，從而使得權重量化更加敏感。相反，也有研究通過縮放權重來優化權重量化，但這會顯著增加激活值的多樣性，進一步加劇激活量化的難度。這些方法的共同缺陷在于：人為設定激活值與權重之間的縮放平衡因子存在局限性，難以實現理想的量化平衡。

為了解決這一問題，我們引入了一種基于分布校正的縮放方法。借鑒已有方法的思想，我們將權重與激活之間的平衡向量設置為可學習參數，并為權重引入了可學習的截斷參數。通過分布校正和比特平衡策略來優化模型性能，我們的目標函數如下：

$arg?min?s,α,β∥WX?Q(clip(W)?diag(s))Q(diag(s)?1?X)∥(1)\underset{s, \alpha, \beta}{\arg\min} \ \| WX - Q(\text{clip}(W) \cdot \text{diag}(s))Q(\text{diag}(s)^{-1} \cdot X) \|\quad(1)$

其中， $W$ 和 $X$ 分別表示全精度權重和激活值， $Q(?)Q(\cdot)$ 表示對權重與激活的量化操作， $clip(?)\text{clip}(\cdot)$ 表示截斷操作， $s$ 為縮放因子，同時定義 $Wmax=α?max?(W)W_{\text{max}} = \alpha \cdot \max(W)$ ， $Wmin=β?min?(W)W_{\text{min}} = \beta \cdot \min(W)$ ，用于控制權重的截斷范圍。

3.2 通過分布校正提升量化效果

我們在對大語言模型進行量化過程中觀察到，不同層對量化的敏感度差異顯著，其中某些層對整體量化性能有關鍵影響。為驗證這一現象，如圖 1 所示，我們在對 LLaMA-7B 模型進行權重-激活全量化的過程中，對各個組成模塊進行了定量分析。實驗發現，對 MLP 和注意力模塊中的 gate proj 和 up proj 層進行量化僅會導致輕微的性能下降，而對 down proj 線性層進行量化則會引發明顯的性能退化。這表明，提升模型量化性能的關鍵在于解決 down proj 層的量化問題。

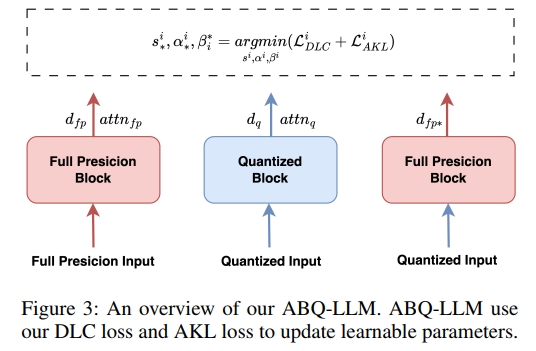
進一步分析發現，導致性能下降的主要原因是 down proj 層中激活值的量化。在 INT4、INT3、INT2 等低比特寬度下，激活值的表達能力受限，導致模型的分布與全精度情況相比發生了嚴重偏移。如圖 3 所示，在進行塊級量化校準時，我們在 down proj 層的輸出上施加雙對數余弦相似度損失，用于修正量化模型的分布。該損失函數被稱為 DLC 損失，記為 $LDLCiL^i_{\text{DLC}}$ 。
$LDLCi=?log(dqi?dfpi∥dqi∥∥dfpi∥)?log(dqi?dfp?i∥dqi∥∥dfp?i∥)(2)\mathcal { L } _ { D L C } ^ { i } = - l o g ( \frac { \boldsymbol { d } _ { q } ^ { i } \cdot \boldsymbol { d } _ { f p } ^ { i } } { \lVert \boldsymbol { d } _ { q } ^ { i } \rVert \lVert \boldsymbol { d } _ { f p } ^ { i } \rVert } ) - l o g ( \frac { \boldsymbol { d } _ { q } ^ { i } \cdot \boldsymbol { d } _ { f p ^ { * } } ^ { i } } { \lVert \boldsymbol { d } _ { q } ^ { i } \rVert \lVert \boldsymbol { d } _ { f p ^ { * } } ^ { i } \rVert } )\quad(2)$
其中， $dqid^i_q$ 表示第 $i$ 個 transformer 塊的量化輸出， $dfpid^i_{fp}$ 表示第 $i$ 個 transformer 塊的全精度輸出， $dfp?id^i_{fp*}$ 表示該塊在輸入來自第 $i ? 1$ 個 transformer 塊的量化輸出情況下的全精度輸出。

此外，我們還分析了 LLaMA-7B 模型中解碼器各層的輸入與輸出激活之間的余弦相似度。結果表明，模型的前幾層和最后幾層的余弦相似度存在顯著差異，表明這些層對模型推理性能有較大影響。為此，我們在這些層的 down proj 層引入了分布補償向量，利用公式 (3) 對其分布偏差進行修正。
$\lceil \frac { W + \gamma a b ^ { \top } } { \Delta } \rfloor + z , 0 , 2 ^ { n } - 1 )\quad(3)$
其中，?·? 表示四舍五入操作， $n$ 表示目標比特寬度， $Δ\Delta$ 表示步長， $z$ 為零點。 $W_q$ 和 $W$ 分別表示量化后的權重和全精度權重。向量 $a$ 和 $b$ 是分布補償向量，其中當 $γ=1\gamma = 1$ 時表示執行補償，當 $γ=0\gamma = 0$ 時表示不進行補償。

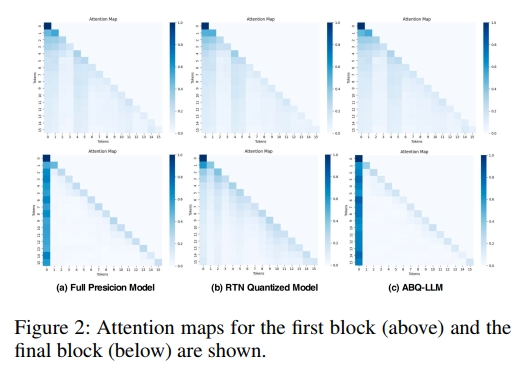
為了提升量化模型的性能，我們分析了量化前后 Attention Map 分布的變化，如圖 2 所示。在全精度模型中，注意力顯著集中在第一個 token 上，凸顯其在引導文本生成過程中的關鍵作用，這一現象也與 LLM-QAT（Liu 等，2023）的結論一致。然而，量化過程會破壞這種注意力分布，使模型對第一個 token 的關注度降低。為了解決這一問題并在量化過程中恢復模型的注意力機制，我們引入了基于注意力的 KL 散度方法，用于重構注意力圖。
$LAKLi=DKL(attnqi∥attnfpi)+DKL(attnfpi∥attnqi)(4)\mathcal { L } _ { A K L } ^ { i } = D _ { K L } ( a t t n _ { q } ^ { i } \parallel a t t n _ { f p } ^ { i } ) + D _ { K L } ( a t t n _ { f p } ^ { i } \parallel a t t n _ { q } ^ { i } )\quad(4)$
其中， $attnqi\text{attn}^i_q$ 表示第 $i$ 個 transformer 塊的量化后注意力圖輸出， $attnfpi\text{attn}^i_{fp}$ 表示同一塊的全精度注意力圖輸出。
在這里插入圖片描述

最后，我們將 DLC 損失與 AKL 損失結合起來，最終的優化目標為：

$s?i,α?i,βi?=arg?min?si,αi,βi(LDLCi+LAKLi)(5)s^i_*, \alpha^i_*, \beta_i^* = \arg\min_{s_i, \alpha_i, \beta_i} (L^i_{DLC} + L^i_{AKL})\quad(5)$

其中， $s^i_*$ 、 $α?i\alpha^i_*$ 和 $βi?\beta_i^*$ 是第 $i$ 個 transformer 塊經過校準后的參數。當量化輸出與全精度輸出的分布匹配時，損失接近于零，從而有效地指導量化過程。

3.3 比特平衡策略

通常，預訓練的大語言模型權重呈現近似正態分布，具有對稱性。通過QQ圖（Quantile-Quantile圖）我們驗證了預訓練模型權重分布的強對稱性（詳見附錄A）。然而，在標準的2比特整數（INT2）量化中，數值表示僅限于四個值，且量化范圍是對稱的，如{-2, -1, 0, 1} 或 {-1, 0, 1, 2}，這破壞了原有的權重對稱分布（詳見附錄A）。這種不對稱導致了顯著的性能下降，如表1所示，性能從W4A16下降到W3A16降低了0.46，而從W3A16下降到W2A16則降低了5.19，降幅非常明顯。

為了解決這種不對稱對LLM量化的影響，我們采用了比特平衡策略，類似于（Li等，2016；Ma等，2024a），將INT2的對稱量化空間擴展為{-2, -1, 0, 1, 2}。這一修改使模型性能恢復到7.50，與W3A16相比處于合理范圍內。

溫馨提示：
閱讀全文請訪問"AI深語解構" ABQ-LLM：用于大語言模型的任意比特量化推理加速