一、相機模型

1.針孔相機模型-外參矩陣

1.世界坐標系到相機坐標系

• 世界坐標系：可以定義空間中任意一個位置，原點位置+三個坐標軸方向=坐標系姿態（X,Y,Z）
• 相機坐標系：定義在相機上，原點是相機中心，z軸沿著相機朝向，需要定義Y軸上下

點的世界坐標：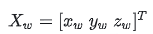

點相機坐標：

剛體變換：旋轉+平移 -> 齊次坐標形式（兩個坐標系的轉換）

逆變換（相機坐標系到世界坐標系）：

2.相機中心在世界坐標系中的位置

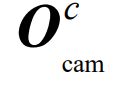：相機中心在相機坐標系中的坐標為0

相機中心在世界坐標系中的坐標

2.相機模型-內參矩陣

1.相機坐標系到歸一化像平面坐標系

歸一化像平面是虛擬的平面坐標，它與物理像平面平行，且距離相機光心距離為f=1

2.歸一化像平面坐標系到物理像平面坐標系—小孔成像過程

3.歸一化像平面到像素坐標系

一般以左上角為坐標原點，需要進行坐標系平移

整體轉換流程如下所示：

3.2D-2D的對極幾何約束

• x1, x2像素坐標
• x1^, x2^ 相機坐標

本質矩陣的對極約束是對相機坐標系下的對極約束。

基礎矩陣的對極約束是對像素坐標系下的對極約束。

**3.1 **2D-2D:對極幾何——基礎矩陣F

性質：

• 3x3的矩陣，秩為2->不可逆
• 具有7個自由度，沒有尺度少了一個自由度，秩為2少一個自由度
• 奇異值為： [𝜎1,𝜎2,0]𝑇
• 極線約束：

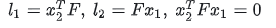
求解方法：

• 直接線性變換法
  • 8點法
  • 最小二乘法
• 基于RANSAC的魯棒方法

3.2 2D-2D:對極幾何——RANSAC

RANSAC——隨機一致性采樣

• N：樣本點個數
• K：求解模型需要最少的點的個數
• 流程：
• 1）隨機采樣 K 個點
• 2）對該 K個點擬合模型
• 3）計算其它點到擬合模型的距離 小于一定閾值，當作內點，統計內點個數
• 4）重復 M 次，選擇內點數最多的模型
• 5）利用所有的內點重新估計模型(可選)