基本概念說明

數據結構

定義：數據結構(Data Structure)是計算機存儲、組織數據的方式，指相互之間存在?種或多種特定關系的數據元素的集合。沒有?種單?的數據結構對所有用途都有用（要考慮適配、效率問題，在不同情況下使用合適的數據結構提高效率）
如：線性表、樹、圖、哈希等
功能：

1. 存儲數據
2. 組織數據：增刪改查數據

算法

定義：算法(Algorithm):就是定義良好的計算過程，他取一個或一組的值為輸入，并產生出一個或一組值作為輸出。簡單來說算法就是一系列的計算步驟，用來將輸入數據轉化成輸出結果。
算法都有好壞之分——就由復雜度來衡量
而數據結構和算法是不分家的

復雜度引入

我們來做一道算法題
https://leetcode.cn/problems/rotate-array/description/


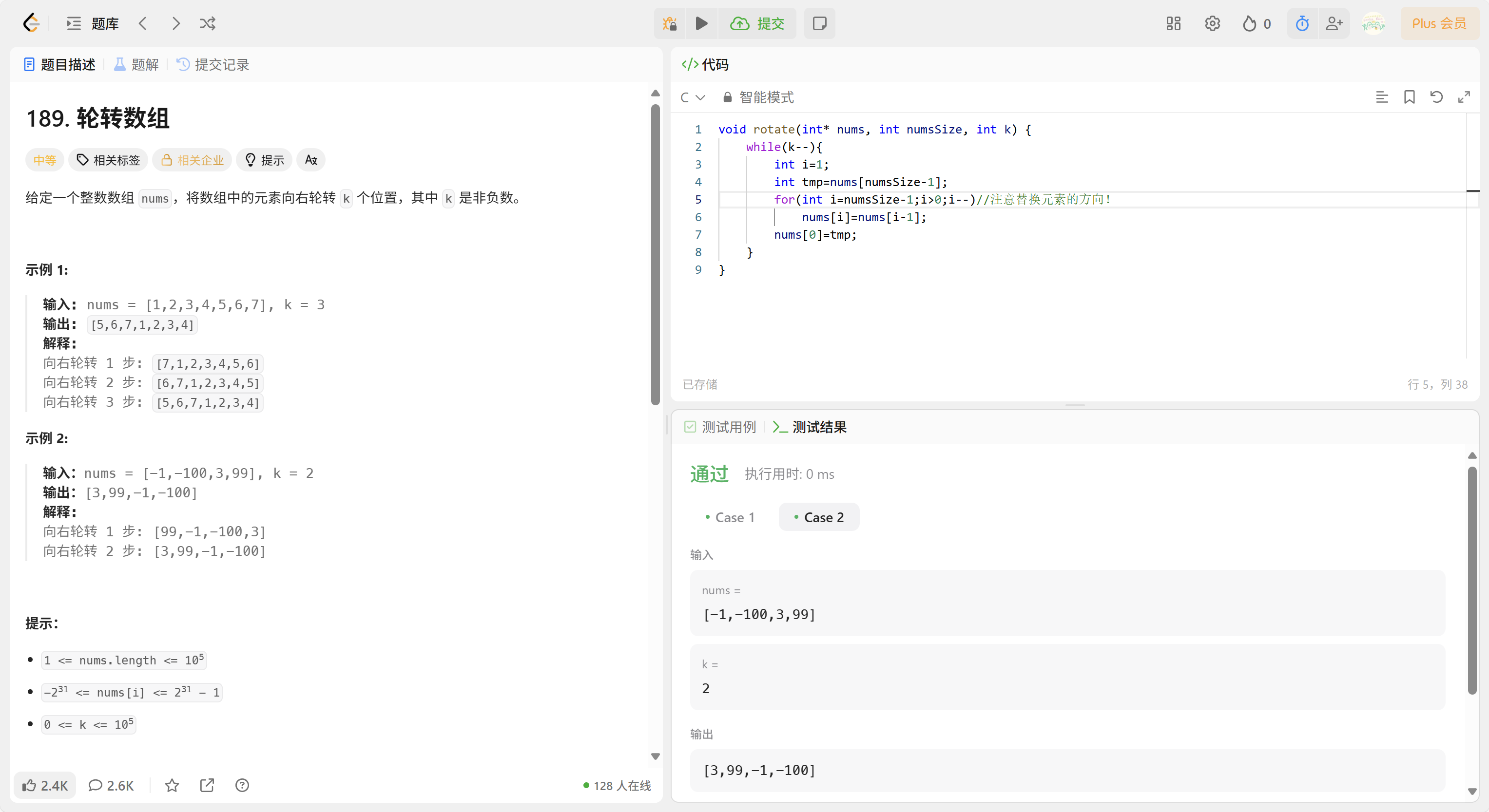
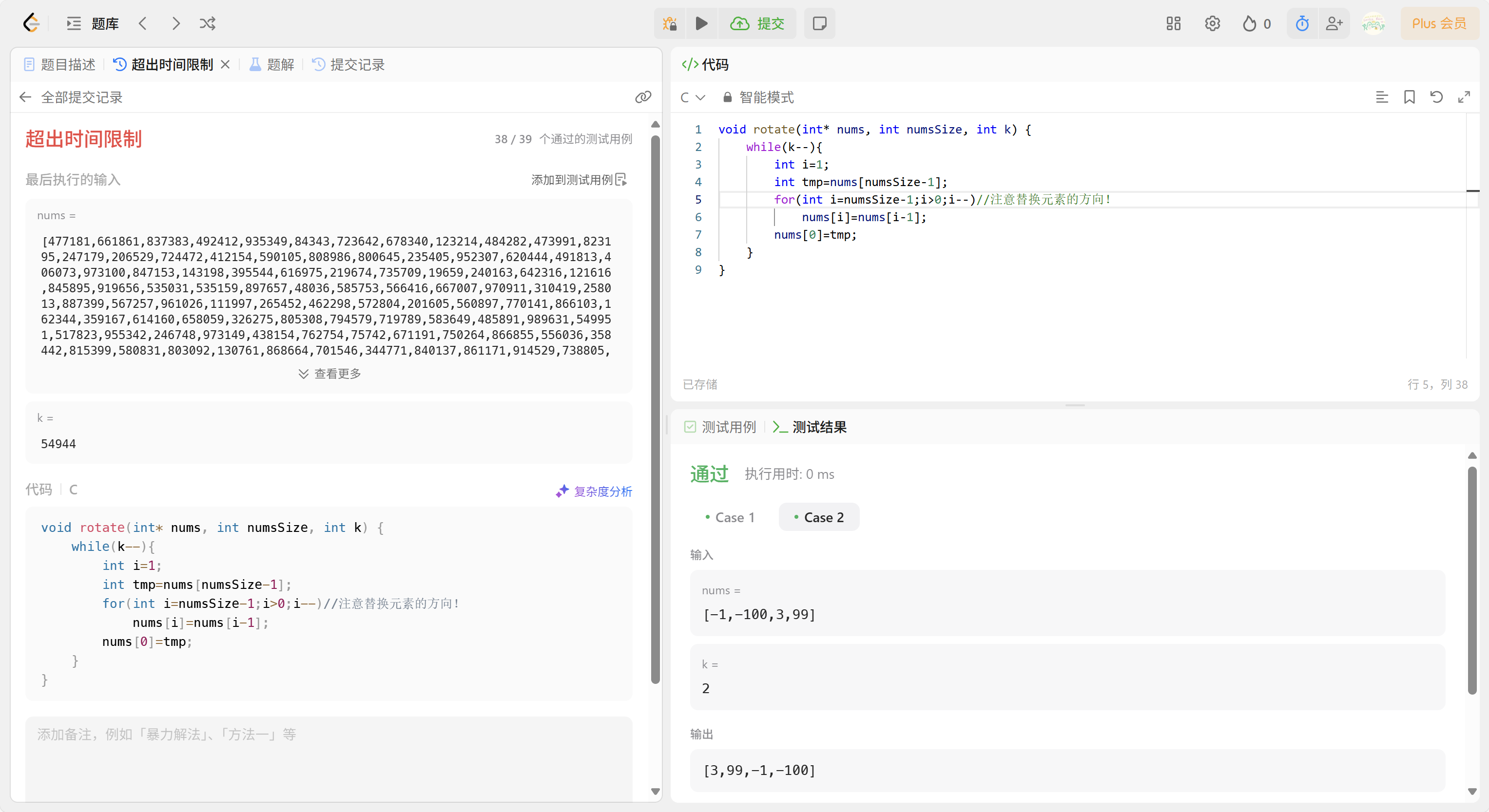
自測運行通過，但是提交后的樣例測試沒有全部通過——代碼所使用的算法不夠好？
我們是否可以通過一些清晰的表達方法明確地表示算法的好壞呢？

復雜度的概念

算法在編寫成可執行程序后，運行時需要耗費時間資源和空間(內存)資源 。因此衡量?個算法的好壞，?般是從時間和空間兩個維度來衡量的，即時間復雜度和空間復雜度。
時間復雜度主要衡量?個算法的運行快慢，而空間復雜度主要衡量?個算法運?所需要的額外空間。
在計算機發展的早期，計算機的存儲容量很小。所以對空間復雜度很是在乎。但是經過計算機行業的迅速發展，計算機的存儲容量已經達到了很?的程度。所以我們如今已經不需要再特別關注?個算法的空間復雜度。
（但是我們也不能隨意浪費空間！）
時間復雜度和空間復雜度都使用大O的漸進表示法來表示，復雜度是一個函數式。

大O的漸進表示法

大O符號（Big O notation）：是用于描述函數漸進行為的數學符號

推導大O階規則

1. 復雜度函數式T(N)中，只保留最高階項，去掉那些低階項，因為當N不斷變大時，低階項對結果影響越來越?，當N無窮時，就可以忽略不計了。
2. 如果最高階項存在且不是1，則去除這個項目的常數系數，因為當N不斷變大，這個系數對結果影響越來越小，當N無窮大時，就可以忽略不計了。
3. T(N)中如果沒有N相關的項目，只有常數項，用常數1取代所有加法常數。

有些算法的時間復雜度存在最好、平均和最壞情況。
最壞情況：任意輸入規模的最大運行次數(上界)
平均情況：任意輸入規模的期望運行次數
最好情況：任意輸入規模的最小運行次數(下界)
大O的漸進表示法在實際中?般情況關注的是算法的上界，也就是最壞運行情況。

時間復雜度運算

在計算機科學中，算法的時間復雜度是?個函數式T(N)，它定量描述了該算法的運?時間。
實際中我們計算時間復雜度時，計算的也不是程序的精確的執?次數，精確執?次數計算起來還是很?煩的(不同的?句程序代碼，編譯出的指令條數都是不?樣的)，計算出精確的執?次數意義也不?，因為我們計算時間復雜度只是想?較算法程序的增?量級，也就是當N不斷變?時T(N)的差別，當N不斷變?時，常數和低階項對結果的影響很?，所以我們只需要計算程序能代表增?量
級的?概執?次數，復雜度的表?通常使??O的漸進表?法。
1.


2.


3.

5.

空間復雜度運算

空間復雜度也是?個數學表達式，是對?個算法在運?過程中因為算法的需要額外臨時開辟的空間。空間復雜度不是程序占?了多少bytes的空間，因為常規情況每個對象??差異不會很?，所以空間復雜度算的是變量的個數。
空間復雜度計算規則基本跟實踐復雜度類似，也使??O漸進表?法。
注意：函數運?時所需要的棧空間(存儲參數、局部變量、?些寄存器信息等)在編譯期間已經確定好了，因此空間復雜度主要通過函數在運?時候顯式申請的額外空間來確定。
1.

常見復雜度對比

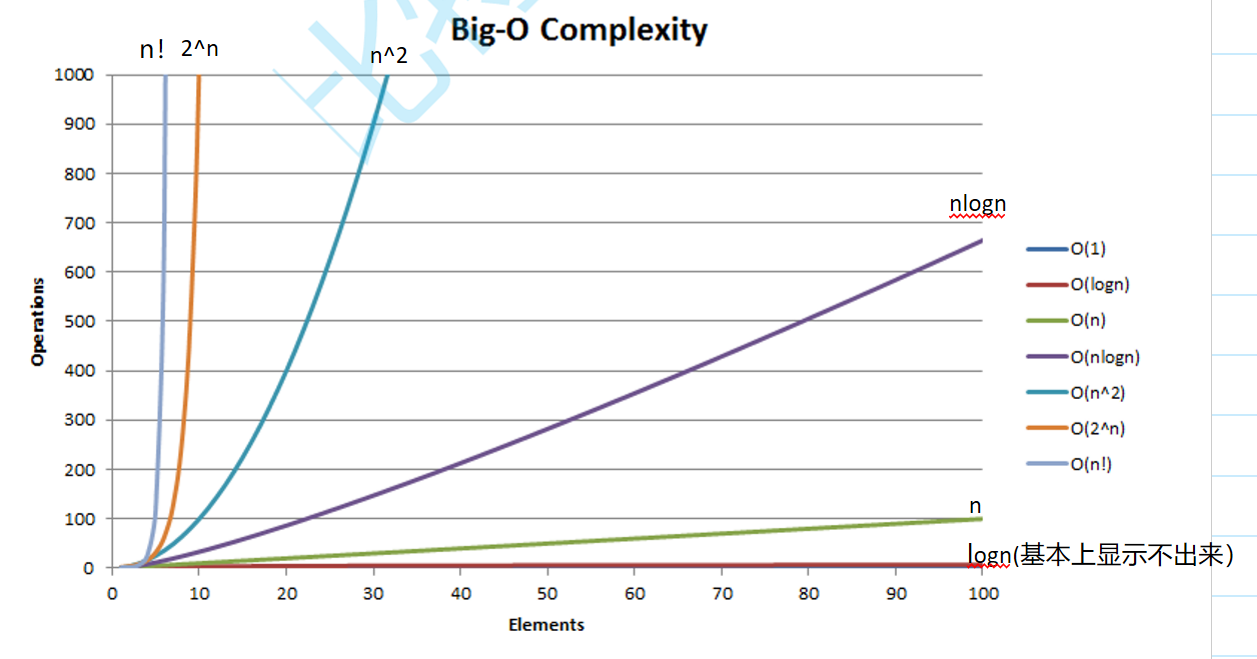
復雜度算法題

最后我們再回到一開始的算法題

法一

審視一下最開始的算法的時間復雜度——O(n^2)。

void rotate(int* nums, int numsSize, int k) {while(k--){int i=1;int tmp=nums[numsSize-1];for(int i=numsSize-1;i>0;i--)//注意替換元素的方向！nums[i]=nums[i-1];nums[0]=tmp;}
}

這種算法由于超出時間限制導致測試不通過，就是因為時間復雜度太高，所以現在我們需要進行優化、或者想出其他時間復雜度更低算法來解決問題。

法二：重新創建一個新數組，把nums中的元素按規律重新安置——只需要遍歷一次nums數組就可完成——時間復雜度O(n)

(只要有思路，寫具體代碼之前就可以把時間復雜度寫出來了）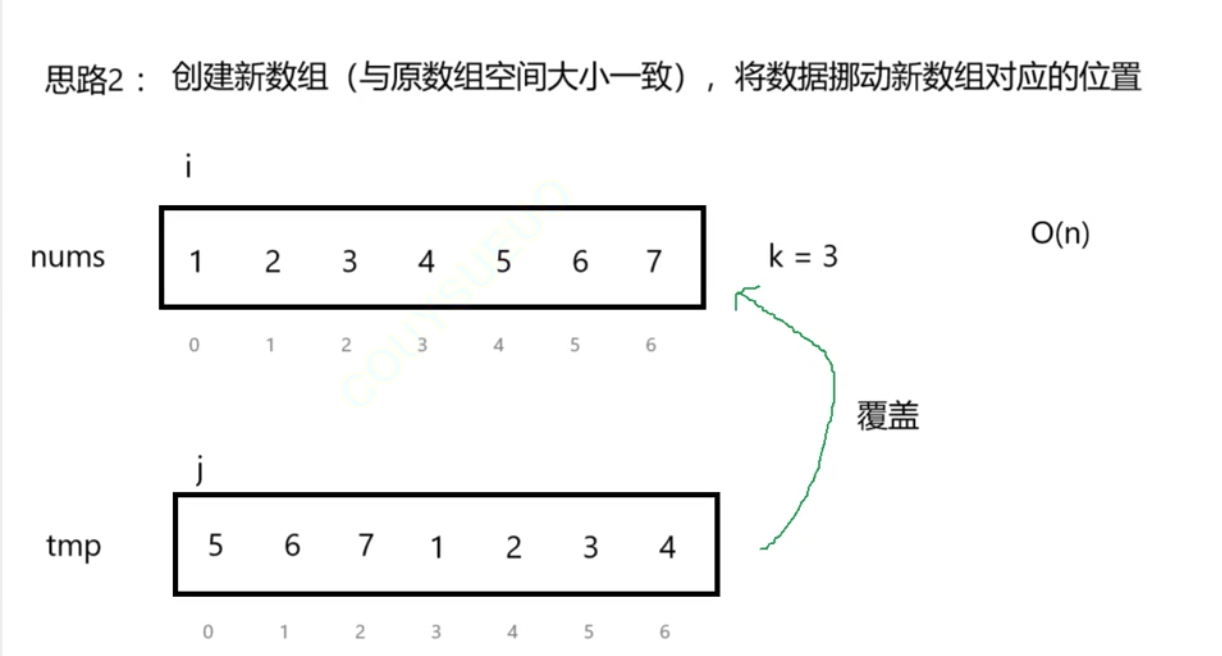

void rotate(int* nums, int numsSize, int k) {int newArray[numsSize];for(int i=0;i<numsSize;i++){newArray[(i+k)%numsSize]=nums[i];//巧用取模解決越界問題，不需要if語句分類討論了}//將新數組導入到原數組中for(int j=0;j<numsSize;j++){nums[j]=newArray[j];}
}

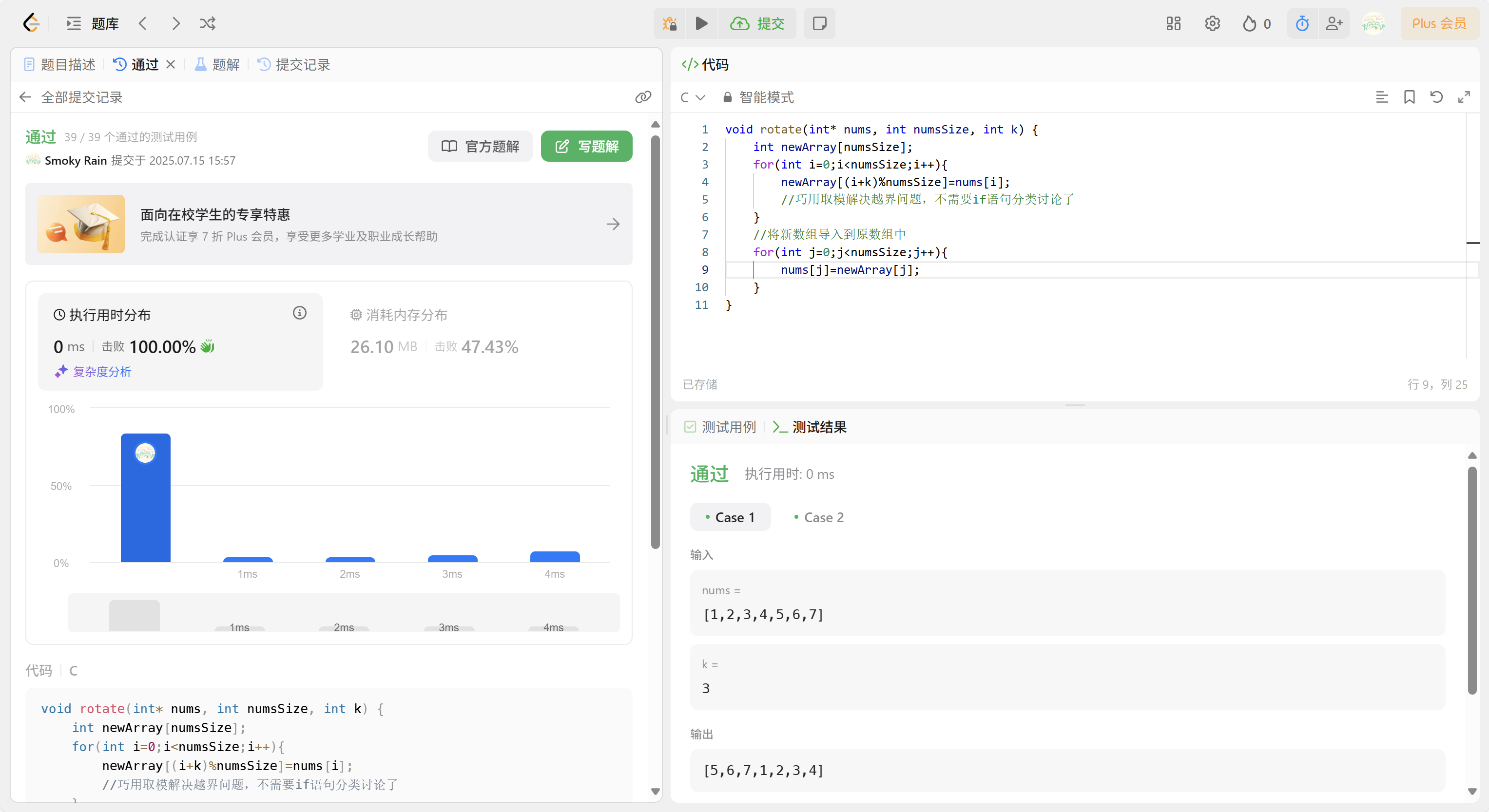
空間復雜度是O(n)，因為運行時開辟臨時變量數組另外申請了numsSize個int的空間，而反觀最開始的方法一，空間復雜度為O(1)
所以我們稱法二是一種“用時間換空間”的方法。

法三：三次逆置

void reverse(int* nums,int left,int right){while(left<right){int tmp=nums[left];nums[left]=nums[right];nums[right]=tmp;left++;right--;}
}
void rotate(int* nums, int numsSize, int k) {reverse(nums,0,numsSize-k-1);reverse(nums,numsSize-k,numsSize-1);reverse(nums,0,numsSize-1);
}

但是這樣寫的代碼運行是正確的，但是不是所有樣例都通過

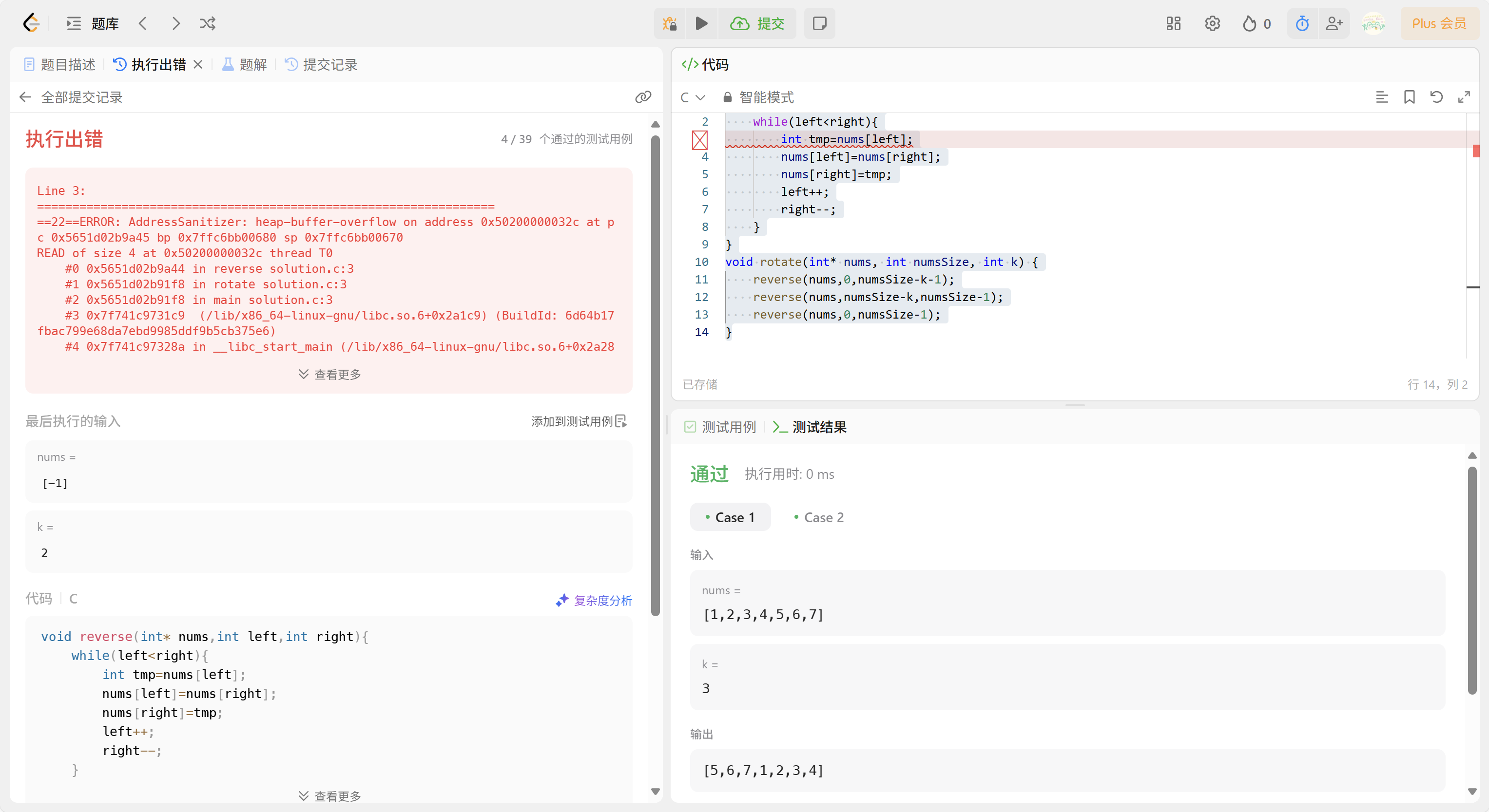
看上圖分析可以得出，這是因為當k>numsSize時，這種方法會導致反轉時出現數組編號為負數的越界問題。
只需要多寫一句k%=numsSize即可避免越界情況。

void reverse(int* nums,int left,int right){while(left<right){int tmp=nums[left];nums[left]=nums[right];nums[right]=tmp;left++;right--;}
}
void rotate(int* nums, int numsSize, int k) {k%=numsSize;reverse(nums,0,numsSize-k-1);reverse(nums,numsSize-k,numsSize-1);reverse(nums,0,numsSize-1);
}

此算法
時間復雜度：O(n)
空間復雜度：O(1)