SAE(Sparse Autoencoders)稀疏自編碼器
0.引言
大模型一直被視為一個“黑箱”,研究人員對其內部神經元如何相互作用以實現功能的機制尚不清楚。因此研究機理可解釋性(Mechanistic Interpretability)就成為了一個熱門研究方向。大模型的復雜之處在于“疊加”(superposition)現象,即一個神經元的激活可能同時是多個完全不相關特征的組成部分,簡單說例如“哈基狗”的特征可能需要激活一組神經元(我們稱之為集合N),而表達“小黑子”,則需要激活另一組神經元(集合M);疊加現象就意味著,集合N和M之間存在交集,這就導致我們很難通過觀察單個神經元的激活,來斷定它究竟在“想”什么。最理想的情況肯定就是一個神經元對應一個特征,而SAE做的就是這樣的事情,將這種疊加狀態剝離出來,類似一種升維再投影的過程。
1. SAE的工作機制
稀疏自編碼器(SAE)通過一個巧妙的“先擴展、后壓縮”的過程,來解構神經網絡內部復雜的疊加狀態。它首先通過編碼器將輸入向量投射到一個維度遠高于自身的特征空間,然后經由解碼器將其重建回原始維度。其訓練目標看似簡單——讓輸出與輸入盡可能一致,但真正的精髓在于訓練過程中施加的“稀疏性懲罰”。
這個懲罰機制迫使那個高維的中間向量變得極其稀疏,大部分維度上的激活值都因過小而被忽略或置零。這正是SAE設計的核心所在:它認為,之所以會出現多個神經元功能疊加的“雜糅”現象,根源在于表達空間不足。因此,通過提供一個巨大的潛在特征空間,并強制模型每次只使用其中一小部分,SAE就能有效地將不同的特征分離到不同的維度上,力求達到“一個維度代表一個精細特征”的理想狀態。

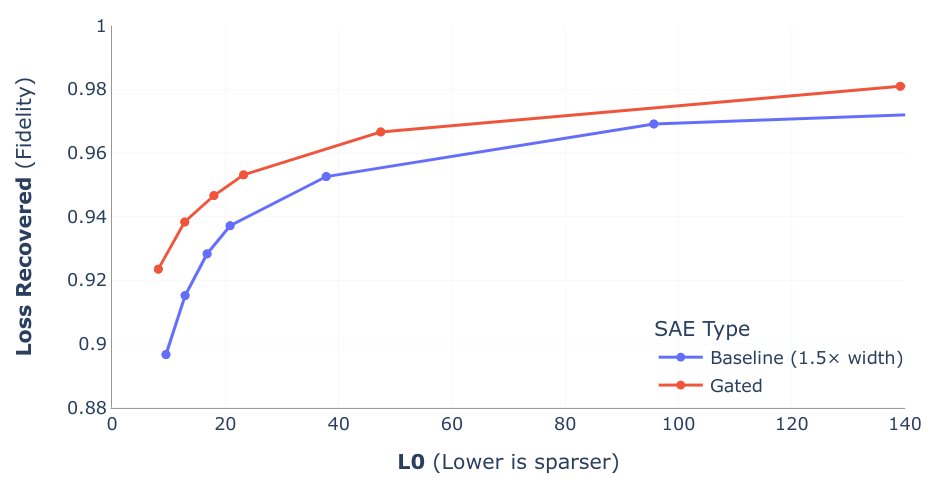
當然,這是一個有損的轉換,總要在重建的“準確性”和特征的“稀疏性”之間做出權衡。SAE的訓練,本質上就是在尋找這個最佳平衡點的旅程。下圖縱軸可以看成代表信息的保留率(信息損失恢復率),橫軸可以看成稀疏向量中激活的個數(L0 范數是衡量一個向量稀疏程度的指標;L0 范數越小,代表這個向量越稀疏),最理想的SAE效果就是接近左上點(0,1)。
理想情況下,SAE表示中的每個激活的數字都對應于某個可理解的組件。假設,當大模型處理一段Python代碼時,其模型內部的一個12288維的激活向量 [0.8, -2.1, 5.5, ...] 對它來說就意味著**“這是一個Python代碼塊”**。這個向量不僅僅代表“代碼”,它還可能包含了代碼的結構、縮進、常見關鍵字等語法風格的復雜信息。
現在,我們有一個SAE,其解碼器是一個形狀為 (49512, 12288) 的巨大矩陣。我們可以把這個解碼器看作是一個擁有49512個“概念定義”的字典,每個“定義”都是一個12288維的向量。
假設,經過訓練,這個SAE中編號為 #8888 的特征,其使命就是專門識別和表示“Python代碼”。那么,該特征對應的解碼器向量(Decoder Vector #8888),就會在數值上非常接近GPT-4內部代表“Python代碼”的那個向量,即約等于 [0.8, -2.1, 5.5, ...]。

2. SAE的應用——如何確定SAE中的特征和實際特征的關系
定性分析:分析最大激活輸入 (Maximally Activating Inputs)
- 首先,在一個非常龐大的、多樣化的數據集(例如包含數十億個句子的文本庫)上運行大語言模型,并記錄下每一個SAE特征在處理每個文本片段時的激活值。
- 然后,針對某一個你感興趣的SAE特征(例如特征編號317),找出那些讓這個特征產生最高激活值的文本輸入。
- 最后,由人類研究員來審查這些“最大激活樣本”,并試圖找出它們之間共同的、可被人類理解的模式或概念。
因果干預 (Causal Interventions)
- 基于第一步的定性分析,假設已經對一個特征有了一個假設(例如,“特征317代表‘哈基狗’這個概念”)。
- SAE的解碼器部分為這個特征學習到了一個向量,這個向量被認為是“哈基狗”這個概念在模型激活空間中的“真實方向”。
- 研究員可以在模型處理任何輸入時,人為地將這個特征的解碼器向量添加到模型的中間激活中。
當Anthropic的研究人員將他們認為是“金門大橋”特征的向量注入到Claude模型的激活中時,Claude在每一個回答中都被迫地開始提及金門大橋。這個實驗強有力地證明了該特征與“金門大橋”這個概念之間的因果關系。
最后,強烈推薦一下Adam Karvonen大佬的https://adamkarvonen.github.io/machine_learning/2024/06/11/sae-intuitions.html筆記,看了十幾個視頻筆記,還是這篇講解得最到位。







)



)


 編譯環境)




