一、單值二叉樹

二叉樹為二叉鏈表形式，結點為：

大概看看題就知道這道題讓我們判斷一個樹到底所有結點的值是不是相同，相同就是單值二叉樹。在實現二叉樹相關操作的時候已經體會到了，遞歸來遍歷二叉樹是非常舒服的（做這些題本質都得遍歷）。

所以我們考慮考慮遞歸怎么個遞歸法，而二叉樹遞歸其實就是考慮根結點以及左右子樹之間的關系。

容易想到判斷根結點與左右孩子結點是否結點，當然，由于需要訪問左右孩子結點，根結點不能為空，而且因為訪問的是三個結點的值，所以肯定三個結點都得先保證不為空。

這個就有點講究了，根結點不能為空，假設剛好遍歷到一個空結點，空結點的值實際上并不是二叉樹實際上的值，對二叉樹是不是單值二叉樹不影響，所以碰見為空返回值需要不影響判斷結果。

接下來就是分別判斷左右子樹是不是也符合了，這個邏輯就簡單了，因為直接上遞歸就行，新的根結點分別是root->left和root->right，其它就沒了。

代碼表達：

只不過最后的遞歸直接省成一個布爾表達式了，因為能走到最后一個retrun語句至少說明根結點和它的左右孩子符合單值二叉樹，如果左右子樹同時符合單值二叉樹，那肯定就是單值二叉樹，但凡出現不符合的情況，我們給出來的語句都可以判斷，且有&&，一個不符合最后都是false。

測試通過：

提交通過：

二、相同的樹

給你一個樹，你得給我判斷出來到底是相同還是不同的，什么是相同的樹呢，結構和數值完全一樣的樹就是相同的樹。比如典例2，典型的數值一樣，但是同樣的根結點，左邊的樹，左孩子為2，右孩子為空；典例3這倆樹不看數值其實是完全一樣的，但是孩子結點的數值并不是一一對應的。

其實說來還是遍歷，只不過是同步遍歷，也就是這樣：

如果同步遍歷完了還沒有檢測出不一樣的結點，顯然就是相同的樹，否則就是不同的樹。

還是立足根結點寫出代碼，再用遞歸去判斷左右子樹的情況。

因為要判斷值，所以肯定保證根不為空，因為兩個根，所以就有三種情況了：

都為空，一個為空（顯然不是相同樹，因為同步遍歷），都不為空。

只不過需要注意的是第二個條件的寫法，全空已經排除過了，那至少有一個為非空，此時就剩下一個空一個非空和全非空，如果再有空豈不是就是一個空一個非空了嘛，直接return false就行，其它都簡單。

三、對稱二叉樹

這道題其實基本不用做了，因為如果相同二叉樹做出來了，那么對稱二叉樹很明顯就是每次遍歷的結點剛好走的路徑相反而已：

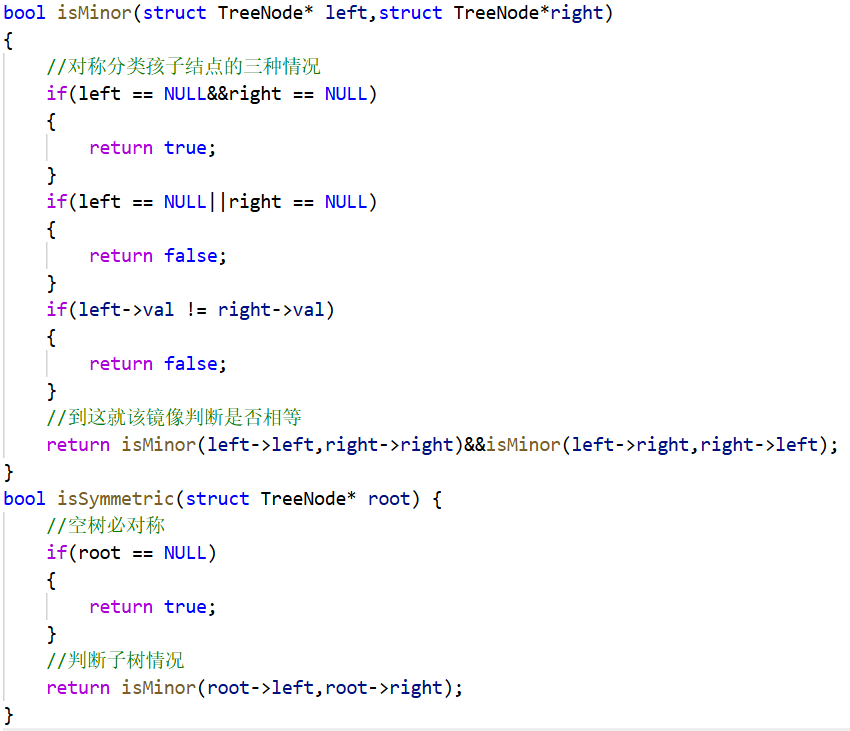
分類基本是模仿相同樹來的，當然，return啥肯定得對著典例寫。

比較容易弄錯的就是最后遞歸按鏡像走路，不過對著典例寫就行。

四、另一棵樹的子樹

其實這個題在我們做過判斷二叉樹是否相同以后就簡單了，遍歷整棵樹，如果找到和subRoot相同根結點的結點的值，這里就可能是子樹可能相同的地點，直接套判斷相同的樹的代碼就可以了。

root防止為空是考慮到了在遍歷的過程中可能一條路走到黑而導致觸發空結點，return false是作為遞歸的終點，代表這條路找不到能與subRoot這個根結點相同的值。

如果找到了，就判斷是否相同，不相同就一直遍歷，直到遍歷完整個樹。

但是代碼一碰見這蔫了，因為找到結點相同的了，就判斷是不是相同，那肯定不同啊，相當于這樣：

這樣能通過就怪了。

想出來個這修改真是艱難，因為判斷相等是肯定要有的，那干脆別以值相等做條件了，萬一前面有跟上面這個例子一樣，遞歸還沒展開，先找到相等的值，那不直接炸了，如果遞歸展開了，就不用老擔心：

這個圖就是遞歸已經展開了才被攔截，最后肯定還是能找到只有1的subRoot。

所以直接一點，改成有相等的樹才能返回true，不然就遍歷完整棵樹后返回false。

五、二叉樹的遍歷（前中后序）

遍歷的思想基本沒啥可講了，但是放在oj題里可沒有那么輕輕松松就能做出來：

比如前序遍歷，最難的其實不是前序遍歷完二叉樹，注意看最后的返回值，要的是int*類型的

但是實際上這道題的意思是最后把遍歷的數據放到數組最后返回數組的地址，這個數組還必須是動態開辟的數組，并且參數returnSize是用來確定遍歷到的二叉樹的結點的個數（最終存到數組內的元素個數）給遠程服務器，前序遍歷簡單，但是一個一個放這些數據就有點講究了。

上來問題就來了，那就是開辟多大空間的數組，那就免不了遍歷二叉樹去計算二叉樹結點個數：

準備好以后就該前序遍歷，并放到數組里：

最重要的就是寫出來怎么把現在遍歷到的根結點放到數組里，畢竟左子樹右子樹的遍歷僅僅是遞歸而已。

容易想到的是必須帶上偏移量，因為每次放置一個元素以后指針肯定要后移：

偏移量肯定不能傳形參，你在Dispose這個函數里面往這次的arr+i所指向的位置存了以后就該++了，但是如果傳值根本不能對偏移量i產生影響。

具體細節：

必須以i的地址為一個變量一直傳給preOrder函數，因為每次遞歸如果不傳i的地址，或者傳值，前者得到的結果就是每次進入新的遞歸以后都會新建一個int i = 0；這樣會造成偏移量實際沒有后移，因為每次進新函數棧幀都是重新定義i；后者傳值不會對偏移量產生影響，這個見過了。

成功通過，經過這道題掌握一種“常駐變量的改變”。

至于中序后序不多bb，調換個位置而已。

六、二叉樹的構建和遍歷

1.先序遍歷字符串構建二叉樹

2.二叉樹中序遍歷并輸出

難的就是第一步，直接畫圖看看最終生成的是一棵什么樣的樹，并在畫圖過程中體會代碼怎么寫：

容易得到，如果碰不到空結點，肯定得一直根左右，那么就是這樣的，接下來該返回到b了，因為c的根左右已經結束了：

緊接著就是遍歷d的左右子樹：

又碰到雙空就得回頭了：

再還原一下，檢驗正確。

最重要的遞歸構建樹：

其實也沒多高級，他說啥是啥，我們只需要注意先序遍歷構建的順序即可。

其它代碼很簡單，直接給出來了：

當然，這里輸入確實偷懶了。