動態規劃熟悉30題 ---上

本來是要寫那個二維動態規劃嘛，但是我今天在問題時候，一個大佬就把他初一時候教練讓他練dp的30題發出來了（初一，啊雖然知道計算機這一專業，很多人從小就學了，但是我每次看到一些大佬從小學還是會很羨慕吧或者說一點點的崇拜，他們都好強，我也想這么強，但我是大一才開始了解，但我之后一定會變強的哈哈），然后說把這30題寫完就差不多對dp熟悉一點點了，然后我就打算先寫這30題的文章，之后再去寫那個二維動態規劃文章，，今天也聽了幾個大佬說，動態規劃除了那些有天賦的人能幾乎一眼看出某個比較難的題的dp數組含義還有他們的遞推公式，其他人都是看題解去理解就好，不用為自己一直看不出來某個題煩，今天還刷到一個視頻，是一個高中生妹妹在講自己一天的經歷，那個高中生妹妹好有活力哈哈，感覺很有精力，她說每天吃到好吃的東西也會很開心，還有談戀愛，不一定要靠談戀愛這個經歷讓自己開心，不要為了談戀愛而談戀愛，朋友也可以讓自己很開心，一定要與自己和解，不要幫助別人一起欺負自己哈哈，話就說到這里哈，接下來我們開始做題，加油，一起變強

P1002 [NOIP 2002 普及組] 過河卒

P1002 [NOIP 2002 普及組] 過河卒 - 洛谷https://www.luogu.com.cn/problem/P1002

題目描述

棋盤上?A?點有一個過河卒，需要走到目標?B?點。卒行走的規則：可以向下、或者向右。同時在棋盤上?C?點有一個對方的馬，該馬所在的點和所有跳躍一步可達的點稱為對方馬的控制點。因此稱之為“馬攔過河卒”。

棋盤用坐標表示，A?點?(0,0)、B?點?(n,m)，同樣馬的位置坐標是需要給出的。

現在要求你計算出卒從?A?點能夠到達?B?點的路徑的條數，假設馬的位置是固定不動的，并不是卒走一步馬走一步。

輸入格式

一行四個正整數，分別表示?B?點坐標和馬的坐標。

輸出格式

一個整數，表示所有的路徑條數。

輸入輸出樣例

輸入 #1復制
6 6 3 3
輸出 #1復制
6
說明/提示

對于?100%?的數據，1≤n,m≤20，0≤?馬的坐標?≤20。

【題目來源】

NOIP 2002 普及組第四題

?思路

這題我們可以很容易看出是類似于走樓梯是吧，我們走的格子是靠上，左這兩個格子的狀態得到的，

首先我們先定義dp數組，走到第i,j格子時候的路徑數量,

然后我們找轉移方程，題上說了卒只能向右和下走，這道題我們所定義的狀態也就是格子，那我們所在的格子的狀態是不是就是靠上和左這倆狀態所轉移，也就是相加。即dp[i][j]=dp[i-1][j]+dp[i][j-1]

接下來就看代碼就好了，對了還有要對最開始的初始位置給初始化,dp[1][1]=1，因為自身就是一條路，所以最開始為1。注意開long long?

#include<bits/stdc++.h>
using namespace std;
long long int dp[50][50];//到達i,j位置時的路徑個數 
//存一下馬能走的位置 
int mvx[]={-1,-2,-1,-2,1,2,1,2,0};
int mvy[]={-2,-1,2,1,2,1,-2,-1,0};
int main(){int n,m,x,y;cin>>n>>m>>x>>y;n++,m++,x++,y++;dp[1][1]=1;//這樣就保證不用初始化了，后續循環從i=1,j=1開始 for(int i=0;i<=8;i++){int x1=x+mvx[i];int y1=y+mvy[i];if(x1>0&&y1>0) dp[x1][y1]=-1;//記錄一下這些坐標不能走 } for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(i==1&&j==1) continue;if(dp[i][j]==-1){dp[i][j]=0;continue;}dp[i][j]=dp[i-1][j]+dp[i][j-1];}}cout<<dp[n][m]; 
}

P1044 [NOIP 2003 普及組] 棧

P1044 [NOIP 2003 普及組] 棧 - 洛谷https://www.luogu.com.cn/problem/P1044

題目背景

棧是計算機中經典的數據結構，簡單的說，棧就是限制在一端進行插入刪除操作的線性表。

棧有兩種最重要的操作，即 pop（從棧頂彈出一個元素）和 push（將一個元素進棧）。

棧的重要性不言自明，任何一門數據結構的課程都會介紹棧。寧寧同學在復習棧的基本概念時，想到了一個書上沒有講過的問題，而他自己無法給出答案，所以需要你的幫忙。

題目描述

寧寧考慮的是這樣一個問題：一個操作數序列，1,2,…,n（圖示為 1 到 3 的情況），棧 A 的深度大于?n。

現在可以進行兩種操作，

將一個數，從操作數序列的頭端移到棧的頭端（對應數據結構棧的 push 操作）
將一個數，從棧的頭端移到輸出序列的尾端（對應數據結構棧的 pop 操作）

使用這兩種操作，由一個操作數序列就可以得到一系列的輸出序列，下圖所示為由?1 2 3?生成序列?2 3 1?的過程。

（原始狀態如上圖所示）

你的程序將對給定的?n，計算并輸出由操作數序列?1,2,…,n?經過操作可能得到的輸出序列的總數。

輸入格式

輸入文件只含一個整數?n（1≤n≤18）。

輸出格式

輸出文件只有一行，即可能輸出序列的總數目。

輸入輸出樣例

輸入 #1復制
3
輸出 #1復制
5
說明/提示

【題目來源】

NOIP 2003 普及組第三題

?思路

先說一下這是卡特蘭數的用法，我就先說一下卡特蘭數一半呢用到的地方在哪

卡特蘭數簡介

卡特蘭數是一個經典的組合數學序列，常見于以下問題：

n個節點的二叉搜索樹有多少種不同形態

包含n對括號的合法表達式有多少種

凸n+2邊形的三角劃分方案數

n個元素的出棧序列有多少種

分割問題為子問題：在 k 出棧之后，剩下的問題可以分為兩個部分：左邊的子問題：處理 1, 2, ....., k-1 的出棧序列。右邊的子問題：處理 k+1, k+2, ...., n 的出棧序列。這兩個子問題的解相互獨立，并且可以組合起來形成原問題的解。

就是怎么說呢，因為入棧的序列是123456這種按順序的，所以當元k素出棧，那一定還有n-k個元素沒出棧對吧，也一定有k-1個元素已經出棧了，是吧，就是這樣分割為子問題。

那我們要求n個元素的出棧順序，他可以是 1或 2或3,....先出棧是吧，那是不是就變成求出n個不同元素先出棧之后的情況，

對于 ?dp[i] ，假設第一個出棧的元素是第 ?k ?個入棧的元素（這里 ?k ?從 1 到 ?i ）。那么在它出棧之前，有 ?k-1 ?個元素已經在它之前入棧并可能出棧，剩下的 ?i-k ?個元素還沒入棧。對于這 ?k-1 ?個元素來說，它們的合法出棧序列數量是 ?dp[k-1] ；對于剩下的 ?i-k ?個元素，它們的合法出棧序列數量是 ?dp[i-k] 。因此，總的合法出棧序列數量就是所有可能的 ?k ?對應的情況之和，即：

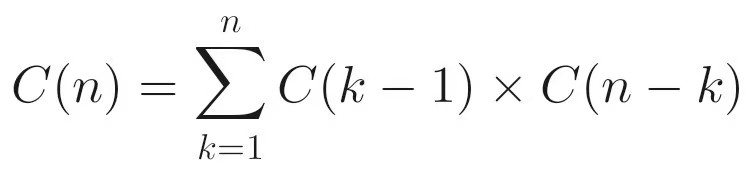
#include<bits/stdc++.h>
using namespace std;
int dp[20];
int n;
int main(){cin>>n;dp[0]=1;//空序列為出棧順序是1dp[1]=1;//一個元素時候出棧順序也為1for(int i=2;i<=n;i++){for(int k=1;k<=i;k++){dp[i]+=dp[i-k]*dp[k-1];}}cout<<dp[n];
}

P1057 [NOIP 2008 普及組] 傳球游戲

P1057 [NOIP 2008 普及組] 傳球游戲 - 洛谷https://www.luogu.com.cn/problem/P1057

題目描述

上體育課的時候，小蠻的老師經常帶著同學們一起做游戲。這次，老師帶著同學們一起做傳球游戲。

游戲規則是這樣的：n?個同學站成一個圓圈，其中的一個同學手里拿著一個球，當老師吹哨子時開始傳球，每個同學可以把球傳給自己左右的兩個同學中的一個（左右任意），當老師再次吹哨子時，傳球停止，此時，拿著球沒有傳出去的那個同學就是敗者，要給大家表演一個節目。

聰明的小蠻提出一個有趣的問題：有多少種不同的傳球方法可以使得從小蠻手里開始傳的球，傳了?m?次以后，又回到小蠻手里。兩種傳球方法被視作不同的方法，當且僅當這兩種方法中，接到球的同學按接球順序組成的序列是不同的。比如有三個同學?1?號、2?號、3?號，并假設小蠻為?1?號，球傳了?3?次回到小蠻手里的方式有?1→2→3→1?和?1→3→2→1，共?2?種。

輸入格式

一行，有兩個用空格隔開的整數?n,m(3≤n≤30,1≤m≤30)。

輸出格式

1?個整數，表示符合題意的方法數。

輸入輸出樣例

輸入 #1復制
3 3
輸出 #1復制
2
說明/提示

數據范圍及約定

對于?40%?的數據，滿足：3≤n≤30,1≤m≤20；
對于?100%?的數據，滿足：3≤n≤30,1≤m≤30。

2008普及組第三題

?思路

首先還是想怎么去定義dp數組，先看要求的東西，我們要求第m次傳給第1個人的方法數，那很明顯跟結果有關系的參數是啥，就是次數和第幾個人，所以我們用二維數組來存儲數據

再看每個人的來源都有啥是不是左邊和右邊人的傳球，那這就是狀態轉移方程了，看代碼

#include<bits/stdc++.h>
using namespace std;
int dp[50][50];
int n,m;
int main(){cin>>n>>m;dp[0][1]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){//向右傳球if(j==n) dp[i][1]+=dp[i-1][j];else{dp[i][j+1]+=dp[i-1][j];}//向左傳球if(j==1) dp[i][n]+=dp[i-1][j];else{dp[i][j-1]+=dp[i-1][j];}}}cout<<dp[m][1];
}

P1077 [NOIP 2012 普及組] 擺花

P1077 [NOIP 2012 普及組] 擺花 - 洛谷https://www.luogu.com.cn/problem/P1077

題目描述

小明的花店新開張，為了吸引顧客，他想在花店的門口擺上一排花，共?m?盆。通過調查顧客的喜好，小明列出了顧客最喜歡的?n?種花，從?1?到?n?標號。為了在門口展出更多種花，規定第?i?種花不能超過?ai??盆，擺花時同一種花放在一起，且不同種類的花需按標號的從小到大的順序依次擺列。

試編程計算，一共有多少種不同的擺花方案。

輸入格式

第一行包含兩個正整數?n?和?m，中間用一個空格隔開。

第二行有?n?個整數，每兩個整數之間用一個空格隔開，依次表示?a1?,a2?,?,an?。

輸出格式

一個整數，表示有多少種方案。注意：因為方案數可能很多，請輸出方案數對?106+7?取模的結果。

輸入輸出樣例

輸入 #1復制運行
2 4
3 2
輸出 #1復制運行
2
說明/提示

【數據范圍】

對于?20%?數據，有?0<n≤8,0<m≤8,0≤ai?≤8。

對于?50%?數據，有?0<n≤20,0<m≤20,0≤ai?≤20。

對于?100%?數據，有?0<n≤100,0<m≤100,0≤ai?≤100。

NOIP 2012 普及組第三題

?思路

這是個多重背包問題，但是咱這里就不管他是啥問題，就一步一步來寫唄

看題目要求啥，要求方案數，跟什么有關。題目說了能排m個花，然后又給了n個種類的花，那我們就可以得到參數是當前用的花的種類數量以及選的花的數量

然后我們要找遞推公式題目給的有限制，一種花只能放a[i]個，所以我們要把每個花放多少個的情況都加起來，嘶我說不清楚我直接在注釋那里加吧

#include<bits/stdc++.h>
using namespace std;
int dp[120][120];
int a[120];
int n,m;
int mod=1e6+7;
int main(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];}dp[0][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){//j就是代表著當前放的花的總數為j時候，放第i種花的情況，不懂的話需要//仔細去分析多想一段時間就行，我想了有二十多分鐘啊，唉我要是天才就好了for(int k=0;k<=min(j,a[i]);k++){(dp[i][j]+=dp[i-1][j-k])%=mod;}}}cout<<dp[n][m];
}

P1091 [NOIP 2004 提高組] 合唱隊形

P1091 [NOIP 2004 提高組] 合唱隊形 - 洛谷https://www.luogu.com.cn/problem/P1091

題目描述

n?位同學站成一排，音樂老師要請其中的?n?k?位同學出列，使得剩下的?k?位同學排成合唱隊形。

合唱隊形是指這樣的一種隊形：設?k?位同學從左到右依次編號為?1,2,?…?,k，他們的身高分別為?t1?,t2?,?…?,tk?，則他們的身高滿足?t1?<?<ti?>ti+1?>?…?>tk?(1≤i≤k)。

你的任務是，已知所有?n?位同學的身高，計算最少需要幾位同學出列，可以使得剩下的同學排成合唱隊形。

輸入格式

共二行。

第一行是一個整數?n（2≤n≤100），表示同學的總數。

第二行有?n?個整數，用空格分隔，第?i?個整數?ti?（130≤ti?≤230）是第?i?位同學的身高（厘米）。

輸出格式

一個整數，最少需要幾位同學出列。

輸入輸出樣例

輸入 #1復制
8
186 186 150 200 160 130 197 220
輸出 #1復制
4
說明/提示

對于?50%?的數據，保證有?n≤20。

對于全部的數據，保證有?n≤100。

思路

這是導彈攔截問題哈，那這個事讓求兩個攔截，就是求一下遞增子序列和遞減子序列，直接遞增子序列是從第0個元素開始，遞減是從第n-1開始這里要注意哦，看代碼吧

#include<bits/stdc++.h>
using namespace std;
int n;
int a[110];
int dpu[110];//遞增
int dpd[110];//遞減
int main(){cin>>n;for(int i=0;i<n;i++){cin>>a[i];}for(int i=0;i<n;i++){dpu[i]=1;for(int j=0;j<i;j++){if(a[i]>a[j]) dpu[i]=max(dpu[i],dpu[j]+1);}}for(int i = n-1; i >= 0; i--) {dpd[i] = 1;  // 初始化為1（至少包含自己）for(int j = i+1; j < n; j++) {if(a[j] < a[i]) {  // 注意是a[j]<a[i]，因為是從i向后的下降序列dpd[i] = max(dpd[i], dpd[j] + 1);}}}int ans=-1;for(int i=0;i<n;i++){
//減去自身那個1ans=max(dpu[i]+dpd[i]-1,ans);}cout<<n-ans;
}

P1095 [NOIP 2007 普及組] 守望者的逃離

P1095 [NOIP 2007 普及組] 守望者的逃離 - 洛谷https://www.luogu.com.cn/problem/P1095

題目背景

NOIP2007 普及組 T3

題目描述

惡魔獵手尤迪安野心勃勃，他背叛了暗夜精靈，率領深藏在海底的娜迦族企圖叛變。

守望者在與尤迪安的交鋒中遭遇了圍殺，被困在一個荒蕪的大島上。

為了殺死守望者，尤迪安開始對這個荒島施咒，這座島很快就會沉下去。到那時，島上的所有人都會遇難。

守望者的跑步速度為?17m/s，以這樣的速度是無法逃離荒島的。慶幸的是守望者擁有閃爍法術，可在?1s?內移動?60m，不過每次使用閃爍法術都會消耗魔法值?10?點。守望者的魔法值恢復的速度為?4?點每秒，只有處在原地休息狀態時才能恢復。

現在已知守望者的魔法初值?M，他所在的初始位置與島的出口之間的距離?S，島沉沒的時間?T。你的任務是寫一個程序幫助守望者計算如何在最短的時間內逃離荒島，若不能逃出，則輸出守望者在剩下的時間內能走的最遠距離。

注意：守望者跑步、閃爍或休息活動均以秒為單位，且每次活動的持續時間為整數秒。距離的單位為米。

輸入格式

輸入數據共一行三個非負整數，分別表示?M，S，T。

輸出格式

輸出數據共兩行。

第一行一個字符串?Yes?或?No，即守望者是否能逃離荒島。

第二行包含一個整數。第一行為?Yes?時表示守望者逃離荒島的最短時間；第一行為?No?時表示守望者能走的最遠距離。

輸入輸出樣例

輸入 #1復制
39 200 4
輸出 #1復制
No
197
輸入 #2復制
36 255 10
輸出 #2復制
Yes
6
說明/提示

對于?30%?的數據，1≤T≤10，1≤S≤100；

對于?50%?的數據，1≤T≤103，1≤S≤104；

對于?100%?的數據，1≤T≤3×105，0≤M≤103，1≤S≤108。

?思路

就先貪一下嘛，先都選60，那個最快的，然后最后再去比較17那個，這個還是挺簡單的，看代碼應該就好哈

#include<bits/stdc++.h>
using namespace std;
int dp[300010];
int m,s,t;
int main(){cin>>m>>s>>t;for(int tt=1;tt<=t;tt++){if(m>=10){m-=10;dp[tt]=dp[tt-1]+60;}else{m+=4;dp[tt]=dp[tt-1];}}for(int i=1;i<=t;i++){dp[i]=max(dp[i],dp[i-1]+17);if(dp[i]>=s){printf("Yes\n%d\n",i);return 0;}}printf("No\n%d\n",dp[t]);return 0;
}

P1358 撲克牌

題目列表 - 洛谷 | 計算機科學教育新生態https://www.luogu.com.cn/problem/list?keyword=1358

題目描述

組合數學是數學的重要組成部分，是一門研究離散對象的科學，它主要研究滿足一定條件的組態（也稱組合模型）的存在、計數以及構造等方面的問題。組合數學的主要內容有組合計數、組合設計、組合矩陣、組合優化等。

隨著計算機科學的日益發展，組合數學的重要性也日漸凸顯，因為計算機科學的核心內容是使用算法處理離散數據。

今天我們來研究組合數學中的一個有趣的問題，也是一個簡單的計數問題：

從一副含有?n?張的撲克牌(每張撲克牌都不相同)中，分給?m?個人，第?i?個人得到?ai??張牌，求一共有幾種分法，這個數可能非常大，請輸出此數模?10007?后的結果。

輸入格式

第一行兩個整數為?n,m。

第二行?m?個整數?ai?。

輸出格式

此數模?10007?后的結果。

輸入輸出樣例

輸入 #1復制
5 2
3 1
輸出 #1復制
20
輸入 #2復制
20 19
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
輸出 #2復制
8707
說明/提示

對于?50%?的數據：ai?=1。

對于?100%?的數據：1≤n≤104，1≤m≤100，0≤ai?≤100。

思路

學大佬的話? ?熱知識楊輝三角可以處理組合數問題我們先搞個用dp數組構造個楊輝三角

我們知道一個數等于他上面數的加左上角的數也就是公式C(n, k) = C(n-1, k) + C(n-1, k-1)

邊界條件處理

C(0,0) = 1：
- 0 個元素選 0 個元素的方案數為 1（空集）
C(n,0) = 1：
- 從任意 n 個元素中選 0 個元素的方案數總是 1

看代碼

#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[110];
int dp[10010][110];
long long ans=1;
int main(){dp[0][0]=1;for(int i=1;i<=10000;i++){dp[i][0]=1;}for(int i=1;i<=10000;i++){for(int j=1;j<=min(i,100);j++){dp[i][j]=dp[i-1][j]+dp[i-1][j-1];dp[i][j]%=10007;}}cin>>n>>m;for(int i=0;i<m;i++){cin>>a[i];(ans*=1LL*dp[n][a[i]])%=10007;n-=a[i];}cout<<ans;}

P1439 【模板】最長公共子序列

P1439 【模板】最長公共子序列 - 洛谷https://www.luogu.com.cn/problem/P1439

題目描述

給出?1,2,…,n?的兩個排列?P1??和?P2??，求它們的最長公共子序列。

輸入格式

第一行是一個數?n。

接下來兩行，每行為?n?個數，為自然數?1,2,…,n?的一個排列。

輸出格式

一個數，即最長公共子序列的長度。

輸入輸出樣例

輸入 #1復制
5 
3 2 1 4 5
1 2 3 4 5
輸出 #1復制
3
說明/提示

對于?50%?的數據，?n≤103；
對于?100%?的數據，?n≤105。

?思路

這題非常的妙啊，就是讓我更加理解了一下dp吧，這題洛谷第一個題解文章寫的確實很好很好，可以看看他的題解

Junior Dynamic Programming——動態規劃初步·各種子序列問題 - 洛谷專欄

我也按照他的解法寫一下吧

依舊先講一下最長上升子序列

1，n^2做法

首先最初時候，最長遞增子序列都是自己本身，長度也就是1，我們定義dp[i]就是以num[i]元素結尾0....i范圍最長上升子序列，

然后，我們開始枚舉i之前的元素j，判斷當前i元素是否大于j，是的話就繼承j的長度+1，否的話就不繼承，（我覺得這個繼承這個詞用的很好很好，雖然這題不難，但確實一下就理解了），這個也是導彈攔截問題的寫法（我上面寫的也有），接下來看代碼

#include<bits/stdc++.h>
using namespace std;
int dp[5010];
int n;
int a[5010];
int main(){cin>>n;for(int i=0;i<n;i++){cin>>a[i];dp[i]=1;}int ans=0;for(int i=0;i<n;i++){for(int j=0;j<i;j++){if(a[i]>a[j]) dp[i]=max(dp[j]+1,dp[i]);ans=max(ans,dp[i]);}}cout<<ans;
}

好我們開始講重點優化，nlogn解法

我們這次dp數組，索引為子序列的長度，然后數值就是相同長度子序列的最小末尾，就比如長度都為2，序列1是1 4，序列2是2 3，那dp[2]就是3（懂了吧），就是這樣子我們以最小末尾做值，我們就能更好的繼承長度，更好的構造最長上升子序列了，

看代碼

#include<bits/stdc++.h>
using namespace std;
int dp[5010];
int n;
int a[5010];
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];dp[i]=0x7fffffff;}int len=1;dp[1]=a[1];for(int i=2;i<=n;i++){if(a[i]>dp[len]) dp[++len]=a[i];else{//找到第一個大于等于a[i]的位置，此時這個長度子序列的末尾就可改成更小的a[i]了int pos=lower_bound(dp+1,dp+len+1,a[i])-dp;dp[pos]=a[i];}}cout<<len;
}

接下來進入正題

依舊先n^2解法

思路就是，dp[i][j]含義是序列1從0....i,序列2從0...j這兩個串的最長公共子序列長度多長

當for循環遍歷到兩個字符相同時候，就變成dp[i][j]=dp[i-1][j-1]+1，因為這倆相同我們就要找這倆字符之前的狀態然后我們繼承這個狀態+1。如果兩個字符不相同，dp[i][j]=max(dp[i-1][j],dp[i][j-1])。當不相同我們要繼承的狀態就不是兩個字符之前的了，因為可能第i和j-1相同，也可能第i-1和j-1相同，所以我們要繼承這兩個狀態最大的那個。看代碼

但是這樣會超時，只要是1e4--1e5就超時了，我們必須要優化

#include<bits/stdc++.h>
using namespace std;
int dp[1010][10010];
int n;
int a[10010];
int b[10100];
int main(){cin>>n;for(int i=0;i<n;i++) cin>>a[i];for(int i=0;i<n;i++) cin>>b[i];for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(a[i-1]==b[j-1]) dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);else{dp[i][j]=max(dp[i][j-1],dp[i-1][j]);}}}cout<<dp[n][n];return 0;}

優化解法nlogn

思路就是，我沒用map存序列1的字符的位置，然后再從map里找到對應序列2每個字符在序列1中的位置是多少，然后我們記錄起來，找到這個記錄起來的數組，最長上升子序列則就是他們的最長公共子序列，我們就完成了由LCS轉化為LIS(這是因為題給的是n的全排列所以可以)

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int n;
int a[N],b[N],mp[N],dp[N], pos[N];
int main(){cin>>n;for(int i=1;i<=n;i++) cin>>a[i],mp[a[i]]=i,dp[i]=0x7fffffff;for(int i=1;i<=n;i++) cin>>b[i],pos[i]=mp[b[i]];int len=1;dp[1]=pos[1];for(int i=2;i<=n;i++){if(pos[i]>dp[len]) dp[++len]=pos[i];else{int p=lower_bound(dp+1,dp+len+1,pos[i])-dp;dp[p]=pos[i];}}cout<<len;return 0;}

P1616 瘋狂的采藥

P1616 瘋狂的采藥 - 洛谷https://www.luogu.com.cn/problem/P1616

此題為紀念 LiYuxiang 而生。

題目描述

LiYuxiang 是個天資聰穎的孩子，他的夢想是成為世界上最偉大的醫師。為此，他想拜附近最有威望的醫師為師。醫師為了判斷他的資質，給他出了一個難題。醫師把他帶到一個到處都是草藥的山洞里對他說：“孩子，這個山洞里有一些不同種類的草藥，采每一種都需要一些時間，每一種也有它自身的價值。我會給你一段時間，在這段時間里，你可以采到一些草藥。如果你是一個聰明的孩子，你應該可以讓采到的草藥的總價值最大。”

如果你是 LiYuxiang，你能完成這個任務嗎？

此題和原題的不同點：

1. 每種草藥可以無限制地瘋狂采摘。

2. 藥的種類眼花繚亂，采藥時間好長好長啊！師傅等得菊花都謝了！

輸入格式

輸入第一行有兩個整數，分別代表總共能夠用來采藥的時間?t?和代表山洞里的草藥的數目?m。

第?2?到第?(m+1)?行，每行兩個整數，第?(i+1)?行的整數?ai?,bi??分別表示采摘第?i?種草藥的時間和該草藥的價值。

輸出格式

輸出一行，這一行只包含一個整數，表示在規定的時間內，可以采到的草藥的最大總價值。

輸入輸出樣例

輸入 #1復制運行
70 3
71 100
69 1
1 2
輸出 #1復制運行
140
說明/提示

數據規模與約定

對于?30%?的數據，保證?m≤103?。
對于?100%?的數據，保證?1≤m≤104，1≤t≤107，且?1≤m×t≤107，1≤ai?,bi?≤104。

思路

這個是完全背包模板，我來說說我對完全背包的理解

題上說求的是可以采到的草藥的最大值，也就是在t時間內采到的最大值，換到背包問題就是，這么大空間能存的最大價值嘛，那么我們的dp數組也就這樣定義，

核心操作

我們就先遍歷每個草藥，再遍歷時間的所有狀態（也就是背包容量的所有情況）然后對每個草藥進行操作（操作就是判斷往里面裝和不往里面裝，因為是完全背包問題，所以每個物品都可以一直裝），看看代碼結合一下

#include<bits/stdc++.h>
using namespace std;
int m,t;
struct drug{
int time;
int value;
}a[10020];
long long int dp[10000020];
int main(){cin>>t>>m;for(int i=1;i<=m;i++){cin>>a[i].time>>a[i].value;}for(int i=1;i<=m;i++){for(int j=a[i].time;j<=t;j++){dp[j]=max(dp[j],dp[j-a[i].time]+a[i].value);}}cout<<dp[t];
}

P1679 神奇的四次方數

題目背景

在你的幫助下，v 神終于幫同學找到了最合適的大學，接下來就要通知同學了。在班級里負責聯絡網的是 dm 同學，于是 v 神便找到了 dm 同學，可 dm 同學正在忙于研究一道有趣的數學題，為了請 dm 出山，v 神只好請你幫忙解決這道題了。

題目描述

將一個整數?m?分解為?n?個四次方數的和的形式，要求?n?最小。例如，當?m=706?時，因為?706=54+34，所以有?n=2。可以證明此時?n?最小。

輸入格式

一行，一個整數?m。

輸出格式

一行，一個整數?n。

輸入輸出樣例

輸入 #1復制
706
輸出 #1復制
2
說明/提

數據范圍及約定

對于?30%?的數據，m≤5000；
對于?100%?的數據，m≤100,000。

思路

這題是完全背包問題，以前是求出來背包里面能放到最大價值，現在是求出放的最小數量，首頁就是每個數的四次方是價值為1的物品，然后就往里放，然后還要把之前的max變成min

#include<bits/stdc++.h>
using namespace std;
int m;
int dp[100010],a[60];
int main(){cin>>m;memset(dp,0x7f,sizeof(dp));//背包的所有容量情況都初始化為很大的值for(int i=1;i<=50;i++){a[i]=i*i*i*i;}dp[0]=0;//最外層遍歷要裝的物品for(int i=1;i<=50;i++){//內層遍歷背包容量for(int j=a[i];j<=m;j++){dp[j]=min(dp[j],dp[j-a[i]]+1);}}cout<<dp[m];
}

P1734 最大約數和

題目描述

選取和不超過?S?的若干個不同的正整數，使得所有數的約數（不含它本身）之和最大。

輸入格式

輸入一個正整數?S。

輸出格式

輸出最大的約數之和。

輸入輸出樣例

輸入 #1復制運行
11
輸出 #1復制運行
9
說明/提示

【樣例說明】

取數字?4?和?6，可以得到最大值?(1+2)+(1+2+3)=9。

【數據規模】

對于?100%?的數據，1≤S≤1000。

?思路

這個是01背包問題，一個數只能放一個，我們先存一下物品，題上說選取若干個不超過s的正整數，題上還說約數（不含其本身），如果物品有1那就含其本身了，所以我沒懂物品重量從2開始，s就是我們的背包容量，然后約數就是物品價值，就這樣

因為01背包一個物品只能放一個，和完全背包區別就是01的內層循環是倒序，然后--就可以保證不會把一個物品多次放進去，好了看代碼

#include<bits/stdc++.h>
using namespace std;
int s;
int a[1010];//需要放入背包的物品
int dp[1010];
int main(){cin>>s;//要從2開始for(int i=2;i<=s;i++){for(int j=1;j<i;j++){if(i%j==0){a[i]+=j;}}}//物品質量為i，價值為a[i]for(int i=2;i<=s;i++){for(int j=s;j>=i;j--){dp[j]=max(dp[j],dp[j-i]+a[i]);}}cout<<dp[s];
}

P2639 [USACO09OCT] Bessie's Weight Problem G

題目描述

Bessie 像她的諸多姊妹一樣，因為從 Farmer John 的草地吃了太多美味的草而長出了太多的贅肉。所以 FJ 將她置于一個及其嚴格的節食計劃之中。她每天不能吃多過?H(5≤H≤45,000)?公斤的干草。 Bessie 只能吃一整捆干草；當她開始吃一捆干草的之后就再也停不下來了。她有一個完整的N(1≤N≤500)?捆可以給她當作晚餐的干草的清單。她自然想要盡量吃到更多的干草。很自然地，每捆干草只能被吃一次（即使在列表中相同的重量可能出現2次，但是這表示的是兩捆干草，其中每捆干草最多只能被吃掉一次）。給定一個列表表示每捆干草的重量?Si?(1≤Si?≤H)?, 求 Bessie 不超過節食的限制的前提下可以吃掉多少干草（注意一旦她開始吃一捆干草就會把那一捆干草全部吃完）。

輸入格式

第一行有兩個由空格隔開的整數?H?和?N。

第?2?到第?N+1?行，第?i+1?行是一個單獨的整數，表示第?i?捆干草的重量?Si?。

輸出格式

第一行一個單獨的整數表示 Bessie 在限制范圍內最多可以吃多少公斤的干草。

輸入輸出樣例

輸入 #1復制運行
56 4
15
19
20
21
輸出 #1復制運行
56
說明/提示

輸入說明

有四捆草，重量分別是?15,19,20?和?21。Bessie 在?56?公斤的限制范圍內想要吃多少就可以吃多少。

輸出說明

Bessie 可以吃?3?捆干草（重量分別為?15,20,21）。恰好達到她的?56?公斤的限制。

?思路

01背包問題，重量和價值都是一樣的其他的沒啥了，就是個模板題

#include<bits/stdc++.h>
using namespace std;
int s;
int a[1010];//需要放入背包的物品
int dp[1010];
int main(){cin>>s;//要從2開始for(int i=2;i<=s;i++){for(int j=1;j<i;j++){if(i%j==0){a[i]+=j;}}}//物品質量為i，價值為a[i]for(int i=2;i<=s;i++){for(int j=s;j>=i;j--){dp[j]=max(dp[j],dp[j-i]+a[i]);}}cout<<dp[s];
}

P2008 大朋友的數字

P2008 大朋友的數字 - 洛谷https://www.luogu.com.cn/problem/P2008

題目背景

在 NOIP2013 的賽場上，常神牛華麗麗的手殘了，小朋友的數字一題只得了?10?分。于是，他要惡搞一下這道題。

題目描述

有一批大朋友（年齡?15?歲以上），他們每人手上拿著一個數字，當然這個數字只有?1?位，也就是?0?到?9?之間。每個大朋友的分數為在他之前的最長不下降子序列中所有數之和。（這個序列必須以它作為結尾！）如有多個最長不下降子序列，那么取編號字典序最小的。現在告訴你有?n?個大朋友，以及他們各自的數字，請你求出他們每個人的分數。

輸入格式

第一行，1?個數?n。

第二行，n?個數，分別表示每個人的數字。

輸出格式

一行，n?個數，分別表示每個人的分數。

輸入輸出樣例

輸入 #1復制
5
1 2 5 3 4
輸出 #1復制
1 3 8 6 10
輸入 #2復制
5
1 7 5 9 6
輸出 #2復制
1 8 6 17 12
說明/提示

【樣例解釋?1】

五個人分數分別為?(1),(1+2),(1+2+5),(1+2+3),(1+2+3+4)。

【樣例解釋?2】

五個人分數分別為?(1),(1+7),(1+5),(1+7+9)?（還有一個?(1,5,9)），(1+5+6)。

【數據規模】

對于?50%?的數據，1≤n≤500；

對于?80%?的數據，1≤n≤103；

對于?100%?的數據，1≤n≤104。

思路

?就是上面講過的上升子序列再順手記錄個和就行，看代碼吧，應該能看懂

#include<bits/stdc++.h>
using namespace std;
int n;
int a[10020];
int b[10010];
int dp[10020];
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];b[i]=1;dp[i]=a[i];}for(int i=1;i<=n;i++){for(int j=1;j<i;j++){if(a[i]>=a[j]){if(b[i]<b[j]+1) {b[i]=b[j]+1;dp[i]=dp[j]+a[i];}}}}for(int i=1;i<=n;i++) cout<<dp[i]<<' ';
}

P1853 投資的最大效益

題目背景

約翰先生獲得了一大筆遺產，他暫時還用不上這一筆錢，他決定進行投資以獲得更大的效益。銀行工作人員向他提供了多種債券，每一種債券都能在固定的投資后，提供穩定的年利息。當然，每一種債券的投資額是不同的，一般來說，投資越大，收益也越大，而且，每一年還可以根據資金總額的增加，更換收益更大的債券。

題目描述

例如：有如下兩種不同的債券：

投資額?4000，年利息?400；
投資額?3000，年利息?250。

初始時，有?10000?的總資產，可以投資兩份債券 1 債券，一年獲得?800?的利息；而投資一份債券 1 和兩份債券 2，一年可獲得?900?的利息，兩年后，可獲得?1800?的利息；而所有的資產達到?11800，然后將賣掉一份債券 2，換購債券 1，年利息可達到?1050；第三年后，總資產達到?12850，可以購買三份債券 1，年利息可達到?1200，第四年后，總資產可達到?14050。

現給定若干種債券、最初的總資產，幫助約翰先生計算，經過?n?年的投資，總資產的最大值。

輸入格式

第一行為三個正整數?s,n,d，分別表示最初的總資產、年數和債券的種類。

接下來?d?行，每行表示一種債券，兩個正整數?a,b?分別表示債券的投資額和年利息。

輸出格式

僅一個整數，表示?n?年后的最大總資產。

輸入輸出樣例

輸入 #1復制運行
10000 4 2
4000 400
3000 250
輸出 #1復制運行
14050
說明/提示

對于?100%?的數據，1≤s≤106，2≤n≤40，1≤d≤10，1≤a≤104，且?a?是?1000?的倍數，b?不超過?a?的?10%。

?思路

就是完全背包，只是這題的背包容量會改，還有就是題上說a是1000倍數，我們要把重量都/1000，這樣就不會RE了，其他都一樣，看代碼吧

#include<bits/stdc++.h>
using namespace std;
int s,n,d;//最初的總資產、年數和債券的種類。
int a[10020],b[10020];
int dp[10000010];
int main(){cin>>s>>n>>d;for(int i=1;i<=d;i++){cin>>a[i]>>b[i];}for(int k=1;k<=n;k++){int m=s/1000; for(int i=1;i<=d;i++){for(int j=a[i]/1000;j<=m;j++){dp[j]=max(dp[j],dp[j-a[i]/1000]+b[i]);}}  s+=dp[m];}cout<<s;}

總結

感覺學的還可以哈哈，可以的可以的，我上面寫的如果有啥不懂的可以問哈（雖然應該沒人看）