一、簡介

莫爾條紋的形成原理-CSDN博客

“莫爾”一詞源于法文“Moire”，其原本的含義是“波動”或者“起波紋的”。早在古代時期，人們便偶然發現，當把兩塊薄的絲綢織物相互疊加放置時，能夠看到一種呈現不規則形態的花紋。此后，人們就把由兩種條紋相互疊加而產生的圖形命名為莫爾條紋。

在1874年的時候，英國著名的物理學家瑞利率先將莫爾條紋當作一種計量測試的手段，由此開創了莫爾測試技術這一嶄新的領域。

從廣義的范疇來講，莫爾測試技術理應涵蓋所有把莫爾圖案作為計量測試手段的各類方法。不過，按照習慣上的說法，它通常是特指利用計量光柵元件來產生莫爾條紋的那一類計量測試方法，也就是我們常說的光柵莫爾條紋法。

時至今日，莫爾條紋已經在科學研究以及工程技術等諸多領域得到了極為廣泛的應用。作為一種精密的計量手段，莫爾條紋可應用于測角、測長、測振等不同的專業領域當中。并且，隨著光電子技術不斷向前發展，莫爾條紋在自動跟蹤、軌跡控制、變形測試以及三維物體表面輪廓測試等方面，同樣有著十分廣泛的應用。

簡單的說就是：

莫爾條紋（Moire Pattern）是一種由兩個周期性圖案重疊時產生的干涉現象，表現為明暗相間的條紋。其原理基于光的干涉和周期結構的相互作用。

?

原本靜止的條紋在移動另一個條紋的時候整個都動起來了?

莫爾條紋是什么？當柵格紙經過“圖案”時，有趣的科學現象發生了_嗶哩嗶哩_bilibili

二、分類

?針對莫爾條紋的形成原理，已經發展出了多種理論，大致可歸納為以下三種：

一，基于遮光原理來闡釋。該理論主張莫爾條紋的產生，是源于一塊光柵的不透光線紋對另一塊光柵透光縫隙產生的遮擋作用。所以，能夠依據光柵副疊合線紋的交點軌跡，去呈現亮條紋的亮度分布情況。
二，基于衍射干涉原理來解釋。按照這一理論，由條紋所構建形成的全新亮度分布，可以通過衍射波之間相互干涉所產生的結果來加以描述。

三，基于傅里葉變換原理來解釋。依據傅里葉變換原理，能夠把光柵副透射光場分解成為具有不同空間頻率的離散分量，而莫爾條紋恰恰是由那些低于光柵頻率的空間頻率項所構成的。
?

三、遮光原理

遮光原理

當兩個具有相似周期或旋轉角度的圖案（如光柵、網格、線條等）重疊時，它們的透光或反射部分會相互調制，產生低頻的、肉眼可見的條紋（莫爾條紋）。這個光柵結構可以是實際光柵，也可以是光柵的像。由于兩塊光柵的柵距相等（或近似相等），并且線紋寬度等于線紋間距，線紋間又有微小的夾角，那么兩塊光柵的線紋必然在空間相交。透過光線的區域形成亮帶，不透光的區域形成暗帶，其余區域介于亮帶與暗帶之間，這樣就構成了清晰的莫爾條紋圖像。

最常用的方法：

幾何法

直觀、簡便只適用于局部；

序數方程法

適用于全場，可導出莫爾條紋方程。

方法1：疊加兩個正弦波柵格

% 設置參數
width = 500; % 圖像寬度
height = 500; % 圖像高度
f1 = 0.05; % 第一個柵格的頻率
f2 = 0.04; % 第二個柵格的頻率
theta = 10; % 第二個柵格的旋轉角度(度)% 創建網格
[x, y] = meshgrid(1:width, 1:height);% 生成第一個正弦波柵格(水平方向)
pattern1 = sin(2*pi*f1*x);
imshow(pattern1, []);
title('正弦波柵格條紋1')% 生成第二個正弦波柵格(旋轉一定角度)
x_rot = x*cosd(theta) + y*sind(theta);
pattern2 = sin(2*pi*f2*x_rot);
imshow(pattern2, []);
title('正弦波柵格條紋2')% 疊加兩個圖案生成摩爾條紋
moire = pattern1 + pattern2;imshow(pattern1, []);
imshow(pattern2, []);% 顯示結果
figure;
imshow(moire, []);
title('正弦波柵格生成的摩爾條紋');
colormap(gray);

正弦波1

正弦波2

合成的摩爾波紋

?方法2：疊加兩個圓形柵格

% 設置參數
width = 500;
height = 500;
f1 = 0.03; % 第一個圓形柵格的頻率
f2 = 0.025; % 第二個圓形柵格的頻率
cx = width/2; % 中心x坐標
cy = height/2; % 中心y坐標% 創建網格
[x, y] = meshgrid(1:width, 1:height);% 計算到中心的距離
r = sqrt((x-cx).^2 + (y-cy).^2);% 生成兩個圓形柵格
pattern1 = sin(2*pi*f1*r);pattern2 = sin(2*pi*f2*r);
imshow(pattern2, []);
title('圓形柵格生成的條紋2')% 疊加生成摩爾條紋
moire = pattern1 + pattern2;% 顯示結果
figure;
imshow(moire, []);
title('圓形柵格生成的摩爾條紋');
colormap(gray);

圓形波1

圓形波2?

圓形摩爾紋?

方法3：疊加兩個不同角度的直線柵格

合成條紋：

?

% 參數設置
N = 512; % 圖像大小
d1 = 20; % 光柵1周期（像素）
d2 = 22; % 光柵2周期（像素）
theta = 5; % 光柵2旋轉角度（度）% 生成光柵1（水平方向）
[x, y] = meshgrid(1:N, 1:N);
grating1 = 0.5 + 0.5 * cos(2*pi*x/d1);% 生成光柵2（旋轉theta角度）
theta_rad = deg2rad(theta);
x_rot = x*cos(theta_rad) + y*sin(theta_rad);
grating2 = 0.5 + 0.5 * cos(2*pi*x_rot/d2);% 疊加光柵生成摩爾條紋
moire_pattern = grating1 .* grating2;% 顯示結果
figure;
subplot(1,3,1); imshow(grating1, []); title('光柵1');
subplot(1,3,2); imshow(grating2, []); title('光柵2');
subplot(1,3,3); imshow(moire_pattern, []); title('摩爾條紋');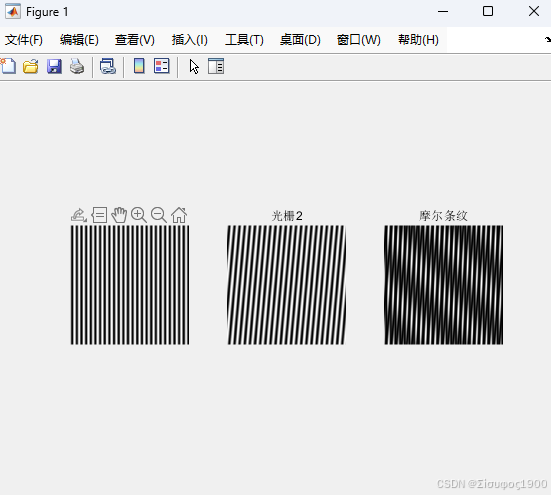

總結：

四、衍射干涉原理

方法一：雙光束干涉

1. 裝置：分束器將激光分為兩束相干光，以微小角度?θ交匯。

2. 干涉：兩束光在重疊區域形成等間距干涉條紋（類似楊氏雙縫），條紋間距?Δx?為：

   

   其中?λ?為光波長。

3. 摩爾條紋：若干涉光柵與另一光柵疊加，會形成次級摩爾條紋。

% 參數設置
N = 512; % 圖像大小
lambda = 10; % 波長（像素）
theta = 0.1; % 兩光束夾角（弧度）% 生成干涉條紋
[x, y] = meshgrid(1:N, 1:N);  % 生成512*512 的圖像
beam1 = exp(1i * 2*pi * sin(theta/2) * x / lambda);
beam2 = exp(1i * 2*pi * sin(-theta/2) * x / lambda);
interference = abs(beam1 + beam2).^2;% 顯示結果
figure;
imshow(interference, []);
title('雙光束干涉條紋');colorbar;

方法二：Talbot 自成像效應

1. 單光柵衍射：一束平行光通過周期性光柵后，在特定距離會自成像。

2. 疊加第二光柵：在 Talbot 距離附近放置第二光柵，與自成像光柵疊加產生摩爾條紋。

% 參數設置
N = 512; % 圖像大小
d = 20; % 光柵周期（像素）
lambda = 632.8e-9; % 波長（m）
z_T = 2 * d^2 / lambda; % Talbot 距離（理論計算）% 生成初始光柵（正弦光柵）
[x, y] = meshgrid(1:N, 1:N);
grating = 0.5 + 0.5 * cos(2*pi*x/d);% 模擬光傳播（菲涅爾衍射）
k = 2*pi/lambda;
z = z_T / 10; % 觀察距離（小于Talbot距離）
propagated = fft2(grating);
[fx, fy] = meshgrid((-N/2:N/2-1)/N, (-N/2:N/2-1)/N);
H = exp(1i * k * z * sqrt(1 - (lambda*fx).^2 - (lambda*fy).^2));
propagated = ifft2(propagated .* fftshift(H));% 疊加第二光柵生成摩爾條紋
grating2 = 0.5 + 0.5 * cos(2*pi*x/(d+2)); % 周期略有不同
moire_talbot = abs(propagated) .* grating2;% 顯示結果
figure;
subplot(1,3,1); imshow(grating, []); title('初始光柵');
subplot(1,3,2); imshow(abs(propagated), []); title('衍射后光場');
subplot(1,3,3); imshow(moire_talbot, []); title('Talbot 摩爾條紋');

五、傅里葉變換原理

?方法1：頻域合成兩光柵的疊加

步驟：

其核心思想是通過頻域操作（如濾波、頻譜疊加）控制空域周期性結構的疊加效果

1. 在頻域生成兩個不同頻率的正弦光柵頻譜。

2. 通過傅里葉逆變換（IFFT）得到空域光柵。

3. 疊加兩光柵生成摩爾條紋。

% 參數設置
N = 512;                % 圖像大小
f1 = 1/20;              % 光柵1的頻率（周期=20像素）
f2 = 1/22;              % 光柵2的頻率（周期=22像素）% 生成頻域坐標
[fx, fy] = meshgrid(-N/2:N/2-1);
fx = fx / N; fy = fy / N;% 生成兩個光柵的頻譜（狄拉克函數模擬理想光柵）
G1 = zeros(N);
G1(abs(fx - f1) < 0.001 & abs(fy) < 0.001) = 1;  % 光柵1（沿x方向）
G2 = zeros(N);
G2(abs(fx - f2) < 0.001 & abs(fy) < 0.001) = 1;  % 光柵2（沿x方向）% 傅里葉逆變換得到空域光柵
grating1 = real(ifft2(ifftshift(G1)));
grating2 = real(ifft2(ifftshift(G2)));% 疊加光柵生成摩爾條紋
moire_pattern = grating1 .* grating2;% 顯示結果
figure;
subplot(1,3,1); imshow(grating1, []); title('光柵1 (頻域生成)');
subplot(1,3,2); imshow(grating2, []); title('光柵2 (頻域生成)');
subplot(1,3,3); imshow(moire_pattern, []); title('摩爾條紋');

?方法2：頻域直接構造摩爾條紋頻譜

1. 摩爾條紋的頻譜是兩光柵頻譜的卷積。

2. 直接在頻域構造卷積后的頻譜，再逆變換得到空域條紋。

3. 

% 參數設置
N = 512;
f1 = 1/20;      % 光柵1頻率
f2 = 1/22;      % 光柵2頻率% 生成頻域坐標
[fx, fy] = meshgrid(-N/2:N/2-1);
fx = fx / N;% 構造兩光柵頻譜的卷積（摩爾條紋頻譜）
moire_spectrum = zeros(N);
moire_spectrum(abs(fx - (f1 - f2)) < 0.001) = 1;  % 低頻摩爾條紋成分% 傅里葉逆變換得到空域摩爾條紋
moire_pattern = real(ifft2(ifftshift(moire_spectrum)));% 顯示結果
figure;
subplot(1,2,1); imshow(log(abs(fftshift(moire_spectrum)) + 1), []); title('摩爾條紋頻譜');
subplot(1,2,2); imshow(moire_pattern, []); title('空域摩爾條紋');

?方法3：通過頻域濾波增強摩爾條紋

1. 對兩光柵疊加后的圖像進行傅里葉變換。

2. 在頻域濾除高頻成分，保留低頻摩爾條紋。

3. 逆變換后得到純凈的摩爾條紋。

% 生成兩光柵疊加的空域圖像（同方法1）
[x, y] = meshgrid(1:N);
grating1 = cos(2*pi*f1*x);
grating2 = cos(2*pi*f2*x);
moire_raw = grating1 .* grating2;% 傅里葉變換
moire_fft = fftshift(fft2(moire_raw));% 設計低通濾波器（保留低頻摩爾條紋）
cutoff = 0.02;  % 截止頻率
H = sqrt(fx.^2 + fy.^2) < cutoff;% 頻域濾波
filtered_spectrum = moire_fft .* H;% 逆變換得到濾波后的摩爾條紋
moire_filtered = real(ifft2(ifftshift(filtered_spectrum)));% 顯示結果
figure;
subplot(1,3,1); imshow(moire_raw, []); title('原始疊加光柵');
subplot(1,3,2); imshow(log(abs(moire_fft) + 1), []); title('原始頻譜');
subplot(1,3,3); imshow(moire_filtered, []); title('濾波后摩爾條紋');

關鍵參數說明

參數	作用
f1, f2	控制兩光柵的頻率，差異越小，摩爾條紋周期越大。
cutoff	低通濾波的截止頻率，影響摩爾條紋的清晰度。
N	圖像分辨率，值越大模擬越精細，但計算量增加。

?六、應用場景

• 精密測量：用于檢測微小位移、形變或振動（如光柵尺）。

• 防偽技術：紙幣、證件上的莫爾圖案用于防偽。

• 圖像處理：消除掃描圖像時的摩爾紋（如去摩爾紋濾鏡）。

• 藝術設計：通過疊加圖案創造動態視覺效果。