文章目錄
- 神經網絡概述
- 神經元模型
- 多層感知機
- 前饋神經網絡
- 網絡拓撲結構
- 數學表示
- 基本傳播公式
- 符號說明
- 整體函數視角
- 卷積神經網絡
- 卷積神經網絡發展簡史
- 第一代(1943-1980)
- 第二代(1985-2006)
- 第三代(2006-至今)
- 快速發展期(2006-2012)
- 爆發期(2012-)
- 卷積神經網絡的結構
- 1. 卷積層
- 2. 激活函數層
- 3. 池化層
- 4. 全連接層
- 卷積神經網絡類型
- AlexNet
- VGGNet
- GoogLeNet
- RestNet
神經網絡概述
神經元模型
- 在神經網絡中,神經元處理單元可以表示不同的對象,例如特征、字母、概念,或者一些有意義的抽象模式。網絡中處理單元的類型分為三類:輸入單元、輸出單元和隱單元。
- 輸入單元接收外部世界的信號與數據
- 輸出單元實現系統處理結果的輸出
- 隱單元是處在輸入和輸出單元之間,不能由系統外部觀察的單元。
- 神經元間的連接權值反映了單元間的連接強度,信息的表示和處理體現在網絡處理單元的連接關系中。

x 1 , . . . , x n x_1,...,x_n x1?,...,xn?是從其他神經元傳來的輸入信號, w i j w_{ij} wij?表示從神經元 j j j到神經元 i i i的連接權值,神經元的輸出可以表示為向量相乘的形式:
n e t i = X W y i = f ( n e t i ) = f ( X W ) net_i=XW \\ y_i=f(net_i)=f(XW) neti?=XWyi?=f(neti?)=f(XW) - 如果神經元的凈激活為正,則稱該神經元處于激活狀態或興奮狀態,如果神經元的凈激活為負,則稱神經元處于抑制狀態。
多層感知機
- 多層感知機(Multi-Layer Perceptron,MLP)是一種前向結構的人工神經網絡,用于映射一組輸入向量到一組輸出向量。MLP可以認為是一個有向圖,由多個節點層組成,每一層全連接到下一層。除輸入節點外,每個節點都是一個帶有非線性激活函數的神經元。
- 多層感知機由輸入層,隱藏層,輸出層,權重和偏置,激活函數組成。
- 輸入層:接收外部信息,并傳遞信息到網絡中。輸入層中的節點并不進行任何計算。
- 隱藏層:一個或多個隱藏層位于輸入層和輸出層之間。每個隱藏層都包含若干神經元,這些神經元具有非線性激活函數,如Sigmoid或Tanh函數。隱藏層的神經元與前一層的所有神經元全連接,并且它們的輸出會作為信號傳遞到下一層。
- 輸出層:輸出層產生網絡的最終輸出,用于進行預測或分類。輸出層神經元的數量取決于要解決的問題類型,例如在二分類問題中通常只有一個輸出神經元,而在多分類問題中則可能有多個輸出神經元。
- 權重和偏置:連接兩個神經元的權重表示這兩個神經元之間聯系的強度。每個神經元還有一個偏置項,它幫助調整神經元激活的難易程度。
- 激活函數:激活函數引入非線性因素,使得神經網絡能夠學習和模擬更復雜的關系。沒有激活函數的神經網絡將無法解決線性不可分的問題。

- 多層感知機通過在訓練過程中不斷調整連接權重和偏置來學習輸入數據中的模式。這種調整通常是通過反向傳播算法實現的,該算法利用輸出誤差來更新網絡中的權重,以減少預測錯誤。
- MLP是感知機的推廣,克服了感知機不能對線性不可分數據進行識別的弱點。MLP本身可以使用任何形式的激活函數,如階梯函數或邏輯S形函數(Logistic Sigmoid Function),但為使用反向傳播算法進行有效學習,激活函數必須限制為可微函數。由于雙曲正切(Hyperbolic Tangent)函數及邏輯S形函數具有良好的可微性,所以經常被用作激活函數。
- 反向傳播算法,在模式識別領域已經成為標準的監督學習算法,并在計算神經學及并行分布式處理領域中獲得廣泛研究。MLP已被證明是一種通用的函數近似方法,可以被用來擬合復雜的函數,或解決分類問題。
- 具體隱藏層神經元數量取決于樣本中蘊含規律的個數以及復雜程度,而樣本蘊含規律的個數往往和樣本數量有關系。確定網絡隱藏層參數的一個辦法是將隱藏層個數設置為超參,使用驗證集驗證,選擇在驗證集中誤差最小的作為神經網絡的隱藏層節點個數。還有就是通過簡單的經驗設置公式來確定隱藏層神經元個數:
l = m + n + α l 為隱藏層節點個數, m 是輸入層節點個數, n 是輸出層節點個數, α 一般是 1 ? 100 的常數 l=\sqrt[]{m+n}+\alpha \\ l為隱藏層節點個數,m是輸入層節點個數,n是輸出層節點個數,\alpha一般是1-100的常數 l=m+n?+αl為隱藏層節點個數,m是輸入層節點個數,n是輸出層節點個數,α一般是1?100的常數
前饋神經網絡
- 在前饋神經網絡(Feedforward Neural Network,FNN)中,每一層的神經元可以接收前一層神經元的信號,并產生信號輸出到下一層。整個網絡中無反饋,信號從輸入層向輸出層單向傳播。
網絡拓撲結構
- 輸入層:第0層神經元(直接接收原始數據)
- 隱藏層:中間所有非線性變換層
- 輸出層:最后一層神經元(產生最終預測結果)
- 單向傳播:信號從輸入層→隱藏層→輸出層單向流動,無反饋回路
數學表示
基本傳播公式
z ( l ) = W ( l ) ? a ( l ? 1 ) + b ( l ) a ( l ) = f l ( z ( l ) ) \begin{aligned} z^{(l)} &= W^{(l)} \cdot a^{(l-1)} + b^{(l)} \\ a^{(l)} &= f_l(z^{(l)}) \end{aligned} z(l)a(l)?=W(l)?a(l?1)+b(l)=fl?(z(l))?
符號說明
| 符號 | 含義 | 維度 |
|---|---|---|
| l l l | 網絡層索引 | 標量 |
| m ( l ) m^{(l)} m(l) | 第 l l l層神經元數量 | 標量 |
| f l ( ? ) f_l(\cdot) fl?(?) | 第 l l l層激活函數 | 非線性函數 |
| W ( l ) W^{(l)} W(l) | 權重矩陣 | R m ( l ) × m ( l ? 1 ) \mathbb{R}^{m^{(l)} \times m^{(l-1)}} Rm(l)×m(l?1) |
| b ( l ) b^{(l)} b(l) | 偏置向量 | R m ( l ) \mathbb{R}^{m^{(l)}} Rm(l) |
| z ( l ) z^{(l)} z(l) | 凈輸入向量 | R m ( l ) \mathbb{R}^{m^{(l)}} Rm(l) |
| a ( l ) a^{(l)} a(l) | 輸出向量 | R m ( l ) \mathbb{R}^{m^{(l)}} Rm(l) |
整體函數視角
將網絡視為復合函數:
a ( L ) = φ ( X , W , b ) a^{(L)} = \varphi(X, W, b) a(L)=φ(X,W,b)
其中:
- 輸入 a ( 0 ) = X a^{(0)} = X a(0)=X
- 參數 W = { W ( 1 ) , . . . , W ( L ) } W=\{W^{(1)},...,W^{(L)}\} W={W(1),...,W(L)}, b = { b ( 1 ) , . . . , b ( L ) } b=\{b^{(1)},...,b^{(L)}\} b={b(1),...,b(L)}
- 輸出 a ( L ) a^{(L)} a(L) 為最終預測結果
卷積神經網絡
- 卷積神經網絡(Convolutional Neural Networks,CNN)是一類包含卷積計算且具有深度結構的前饋神經網絡,它是深度學習框架中的代表算法之一。
卷積神經網絡發展簡史
第一代(1943-1980)
- 1943年:Warren & Walter提出神經元數學模型
- 1958年:Frank實現首個感知機(IBM704),完成形狀分類
- 特點:單層結構,僅解決線性問題
第二代(1985-2006)
- 1985年:Hinton提出BP算法和多隱含層結構
- 1988年:Wei Zhang提出SIANN(醫學圖像應用)
- 1989年:LeCun首創卷積概念(早期LeNet)
- 1998年:LeNet-5加入池化層,MNIST準確率98%
- 瓶頸:受限于計算硬件發展
第三代(2006-至今)
快速發展期(2006-2012)
- 2006年:Hinton提出DBN深度置信網絡
爆發期(2012-)
- 2012年:AlexNet奪冠ImageNet
- 后續模型:ZFNet、VGGNet、GoogLeNet、ResNet、DPRSNet
- 驅動因素:大數據+GPU算力提升
卷積神經網絡的結構
- 卷積神經網絡中隱含層低層中的卷積層與池化層交替連接,高層由全連接層構成。
1. 卷積層
功能:通過卷積核(Filter)提取輸入特征
特性:
- 由可學習的卷積單元組成(通過反向傳播優化)
- 低層提取基礎特征(邊緣/線條),高層提取抽象特征
- 卷積核在輸入圖像上滑動進行局部區域卷積運算
關鍵參數:
| 參數 | 作用 | 影響 |
|---|---|---|
| 卷積核尺寸 | 局部感受區域大小 | 尺寸↑→提取特征更復雜 |
| 步長(Stride) | 滑動步距 | 步長↑→輸出尺寸↓ |
| 填充(Padding) | 邊緣補零層數 | 保持特征圖尺寸,減少邊緣信息丟失 |
2. 激活函數層
- 作用:引入非線性變換(真實數據多為非線性)
- 特性要求:非線性,連續可微,單調性
- 常用函數:Sigmoid、Tanh 、ReLU(最常用)
3. 池化層
- 作用:壓縮特征圖,提取主要特征,簡化網絡計算的復雜度。
- 池化方式:均值池化,最大池化

4. 全連接層
- 全連接層位于卷積神經網絡的最后位置。用于給出最后的分類結果。
- 在全連接層中,特征會失去空間結構,展開為特征向量,并把由前面層級所提取到的特征進行非線性組合得到輸出
f ( x ) = W ? x + b x 為全連接層的輸入, W 為權重系數, b 為偏置 f(x)=W^{*}x+b \\ x為全連接層的輸入,W為權重系數,b為偏置 f(x)=W?x+bx為全連接層的輸入,W為權重系數,b為偏置 - 全連接層連接所有特征輸出至輸出層,對于圖像分類問題,輸出層使用邏輯函數或歸一化指數函數輸出分類標簽;在圖像識別問題中,輸出層輸出為物體的中心坐標、大小和分類;在語義分割中,則直接輸出每個像素的分類結果。
卷積神經網絡類型
AlexNet
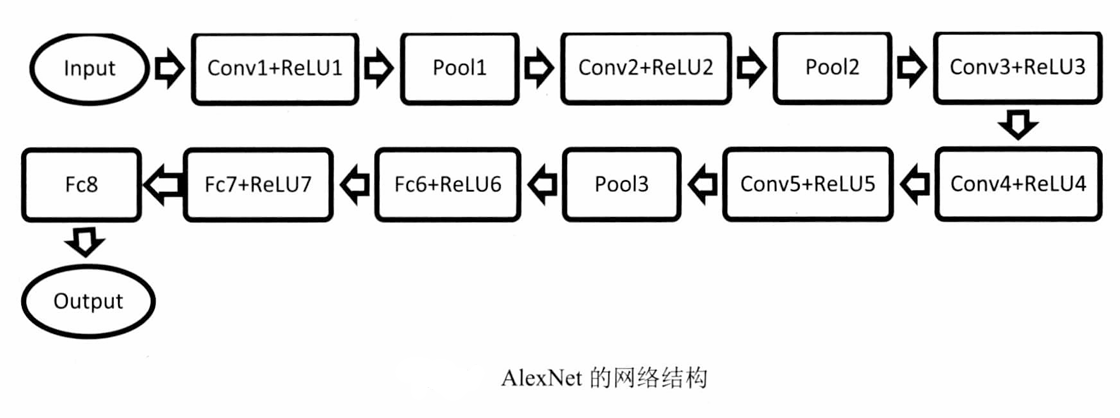
- AlexNet是一種具有里程碑意義的深度卷積神經網絡。AlexNet在2012年的ImageNet大規模視覺識別挑戰賽獲得冠軍,標志深度學習時代的來臨,并奠定了卷積神經網絡在計算機視覺領域的絕對地位。
- AlexNet的成功在于引入新的技術和訓練方法,包括ReLU激活函數、Dropout正則化以及使用GPU進行加速訓練。這些技術的應用極大地提高了網絡的性能,并且對后續的深度學習模型設計產生了深遠的影響。
- AlexNet的網絡結構包括 5 5 5個卷積層和 3 3 3個全連接層。它的輸入圖像尺寸為 227 × 227 × 3 227×227×3 227×227×3(實際輸入尺寸應為 227 × 227 227×227 227×227,由于卷積核大小和步長的設置,之前有文獻提到 224 × 224 224×224 224×224)。網絡中使用了 96 96 96個 11 × 11 11×11 11×11的卷積核對輸入圖像進行特征提取,步長為 4 4 4,沒有使用填充。
VGGNet
- VGGNet探索網絡深度與其性能的關系,通過構筑 16 19 16~19 16?19層深的卷積神經網絡, T o p 5 Top5 Top5誤差率為 7.5 7.5% 7.5,采用 3 x 3 3x3 3x3的卷積核與 2 x 2 2x2 2x2的池化核,網絡結構如圖所示。

- VGGNet包含很多級別的網絡,深度從11層到19層不等,最常用的是VGG-16和VGG-19。
- VGGNet把網絡分成了5段,每段都把多個3x3的網絡串聯在一起,每段卷積后接一個最大池化層,最后是3個全連接層和一個Softmax層。
- VGGNet 核心創新
-
小卷積核堆疊設計
- 使用多層3×3小卷積核替代單層大卷積核(如用2層3×3代替1層5×5)
- 優勢:增強特征提取能力(感受野相同但非線性更強),顯著減少參數量(2層3×3:18n vs 1層5×5:25n)
-
高效訓練策略
- 多尺度訓練與交替訓練結合
- 關鍵層預訓練技術
- 效果:大幅縮短收斂周期
- 局限性:全連接層過多(3個FC層);導致參數量爆炸(占模型總參數90%+);內存/計算資源消耗大
GoogLeNet
- GoogLeNet是由谷歌的研究院提出的卷積神經網絡,獲得2014年的ILSVRC比賽分類任務的冠軍,Top5誤差率僅為6.656%。
- GoogLeNet的網絡共有22層,但參數僅有700萬個,比之前的網絡模型少很多。
- 一般來說,提升網絡性能最直接的辦法就是增加網絡深度,隨之增加的還有網絡中的參數,但過量的參數容易產生過擬合,也會增大計算量。GoogLeNet采用稀疏連接解決這種問題,為此提出了inception結構。

- 在inception結構中,同時采用 1 × 1 、 3 × 3 、 5 × 5 1\times1、3\times3、5\times5 1×1、3×3、5×5卷積核是為了將卷積后的特征保持一致,便于融合 s t r i d e = 1 stride=1 stride=1, p a d d i n g padding padding分別為 0 、 1 、 2 0、1、2 0、1、2,卷積后就可得到相同維度的特征,最后進行拼接,將不同尺度的特征進行融合,使得網絡可以更好地提取特征。
RestNet
- 隨著神經網絡深度的增加,模型準確率會先上升,然后達到飽和,持續增加深度時,準確率會下降;因為隨著層數的增多,會出現梯度爆炸或衰減現象,梯度會隨著連乘變得不穩定,數值會特別大或者特別小。因此,網絡性能會變得越來越差。
- ResNet通過在網絡結構中引入殘差網絡來解決此類問題。殘差網絡結構如圖所示。

- 殘差網絡是跳躍結構,殘差項原本是帶權重的,但ResNet用恒等映射。在圖5-7中,輸入為x,期望輸出為H(x),通過捷徑連接的方式將x傳到輸出作為初始結果,輸出為 H ( x ) = F ( x ) + x H(x)=F(x)+x H(x)=F(x)+x,當 F ( x ) = 0 F(x)=0 F(x)=0時, H ( x ) = x H(x)=x H(x)=x。于是,ResNet相當于將學習目標改變為殘差F(x)=H(x)-x,因此,后面的訓練目標就是要將殘差結果逼近于0。
- ResNet通過提出殘差學習,將殘差網絡作為卷積神經網絡的基本結構,通過恒等映射來解決因網絡模型層數過多導致的梯度爆炸或衰減問題,可以最大限度地加深網絡,并得到非常好的分類效果。


![[Java實戰]Spring Boot 整合 Freemarker (十一)](http://pic.xiahunao.cn/[Java實戰]Spring Boot 整合 Freemarker (十一))



)












