目錄
1.知識回顧
2.關鍵點
特點
三個模版
普通的模版(有局限)
以LeetCode上的一道題為例:704. 二分查找
分析
引入二段性:分兩段,舍一段,操作另一段(這個是二分查找的本質!)
代碼
提交結果
當然也可以使用隨機數來分兩段
普通模版總結
1.知識回顧
之前在C語言專欄中的文章提到了二分查找,可復習:
E7.【C語言】練習：在一個有序數組中查找具體的某個數字n（二分查找）
本文將提煉出一些關鍵點
2.關鍵點
特點
算法細節較多,一 一介紹:
之前講過二分查找的前提: 數組有序時才能使用二分查找,其實并不是這樣!,
當數組滿足某特定規律時,也可以使用二分查找(這個后面會介紹)
三個模版
有以下二分查找的固定格式,做題只需要照葫蘆畫瓢,注意先理解再記憶
普通的模版(有局限)
以LeetCode上的一道題為例:704. 二分查找
https://leetcode.cn/problems/binary-search/description/
給定一個?
n?個元素有序的（升序）整型數組?nums和一個目標值?target?，寫一個函數搜索?nums?中的target，如果目標值存在返回下標，否則返回-1。
示例 1:輸入:nums= [-1,0,3,5,9,12],target= 9 輸出: 4 解釋: 9 出現在nums中并且下標為 4示例?2:
輸入:nums= [-1,0,3,5,9,12],target= 2 輸出: -1 解釋: 2 不存在nums中因此返回 -1提示：
- 你可以假設
nums?中的所有元素是不重復的。n?將在?[1, 10000]之間。nums?的每個元素都將在?[-9999, 9999]之間。
分析
暴力解法直接從左向右或從右向左找,這里不寫,講講暴力解法的缺陷:每次只能比較一個數,時間復雜度為
注意到題目條件"一個?n?個元素有序的（升序）整型數組?nums ",那么可以利用數組的單調性對暴力解法優化
以nums = [-1,0,3,5,9,12], target = 9為例說明,現查找到3,發現target>3且數組單增,那么3的左側是不需要查找的,繼續查找3的右側
引入二段性:分兩段,舍一段,操作另一段(這個是二分查找的本質!)
對于上述單增數組有許多分段方式:
1.二分
即近似分成二等分
2.三分
將數組近似分成三等分
然后任意選一個節點來分段,例如:
3.四分
將數組近似分成四等分......
......
當然也可以使用隨機數來分段
其中二分的時間復雜度是最低的,時間復雜度為,當然某些情況下使用隨機數來分段時間復雜度也比較低
算法:設數組是單調遞增的,對它平分兩段:
比較nums[mid]和num[target]的大小,
1.nums[mid]==num[target],結束循環,返回結果
2.nums[mid]
num[target],依據二段性:分兩段,舍一段,操作另一段
,舍棄[left,mid]段,去[mid,right]段尋找,那么更新left
left=mid+1;//right不變nums[mid]
num[target],返回結果,依據二段性:分兩段,舍一段,操作另一段
,舍棄[mid,right]段,去[left,mid]段,那么更新right
right=mid-1;//left不變3.更新mid(有多種方法,上面提過了)
只需要循環上面三步,變化尋找的區間,最終一定可以找到結果
結束循環的兩個條件:
1.nums[mid]==num[target],直接返回結果
2.leftright,(注:left==right,分的段是一個"點",只有一個元素,但也需要判斷是否等于target,仍然需要循環),沒有找到target
那么循環的條件是:leftright
代碼
class Solution {
public:int search(vector<int>& nums, int target) {int left=0;int right=nums.size()-1;int mid;while(left<=right){mid=left+(right-left+1)/2;if (nums[mid]==target)return mid;if (nums[mid]>target)right=mid-1;if (nums[mid]<target)left=mid+1; }return -1;//沒找到target}
};
注:mid不要寫成(left+right)/2!之前在L42.【LeetCode題解】四數之和(雙指針思想) 從匯編角度分析報錯原因文章提到過報錯的原因,當數組過長時,加法可能導致溢出
防溢出的方法:(left+right)/2改為left+(right-left)/2或left+(right-left+1)/2
提交結果
同理三分法只需要將除數2改成3即可,四分法、五分法同理
mid=left+(right-left+1)/3;當然也可以使用隨機數來分兩段
class Solution {
public:int search(vector<int>& nums, int target) {srand((unsigned int)time(nullptr));int left=0;int right=nums.size()-1;int mid;while(left<=right){mid=left+rand()%(right - left + 1);if (nums[mid]==target)return mid;if (nums[mid]>target)right=mid-1;if (nums[mid]<target)left=mid+1; }return -1;}
};注: 循環體中,如果最后更新mid將導致除0錯誤!
這樣寫是錯誤的:
class Solution {
public:int search(vector<int>& nums, int target) {srand((unsigned int)time(nullptr));int left=0;int right=nums.size()-1;int mid=left+rand()%(right - left + 1);while(left<=right){if (nums[mid]==target)return mid;if (nums[mid]>target)right=mid-1;if (nums[mid]<target)left=mid+1;mid=left+rand()%(right - left + 1); }return -1;}
};
排查錯誤:
VS中進入調試模式
發生錯誤的地方是:?mid = left + rand() % (right - left + 1),則mid=2+rand()%(1-2+1)=2+rand()%0,為除0錯誤,此時left仍然<=right,策略:先更新mid的值,這樣進行if判斷時能修改left和right的值,能及時退出循環,防止除0錯誤
提交結果:
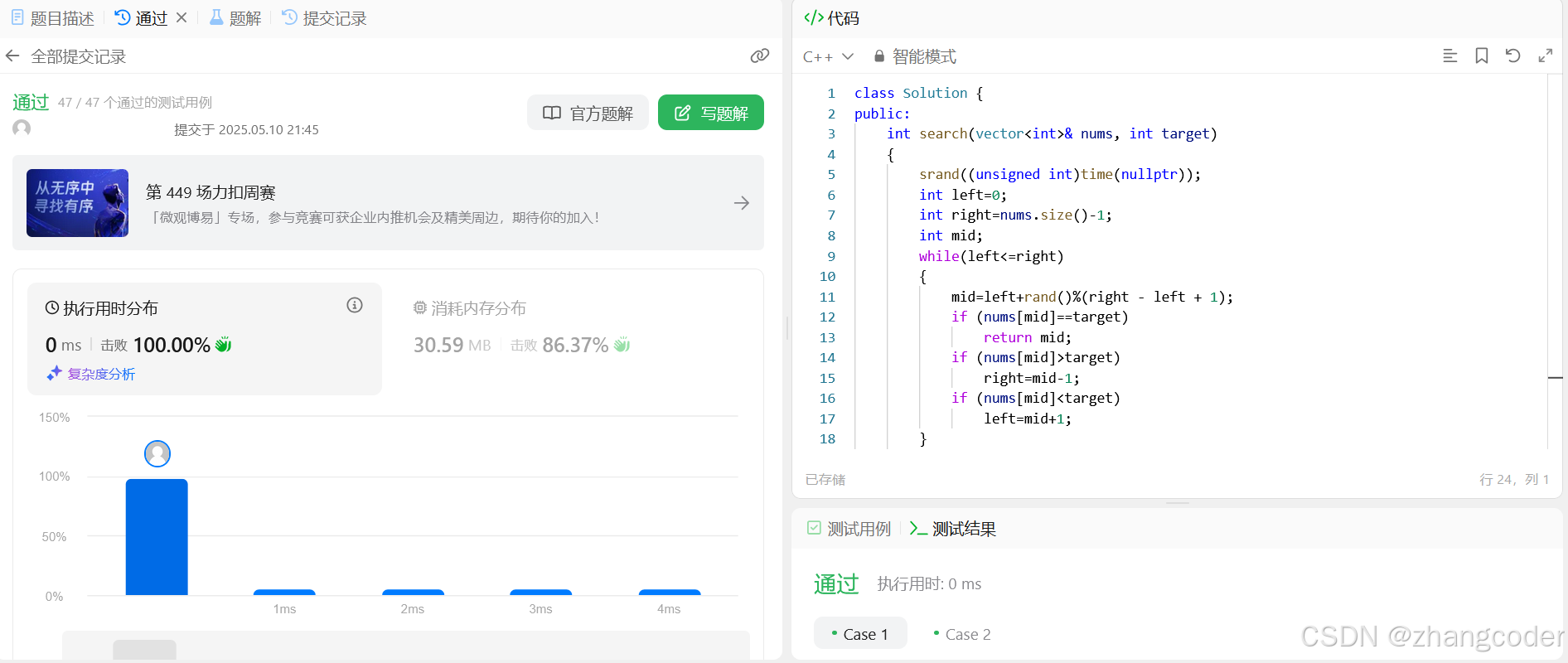
普通模版總結
利用二段性填以下模版空缺的地方:
while(left<=right)
{int mid=left+(right-left+1)/2;if (......)return mid;if (......)right=mid-1;if (......)left=mid+1;
}注意1.判斷條件 2.mid防溢出方法 3.left和right的更新方式
其他兩個模版見下一篇文章
：實際案例)
