數據結構--AVL樹

前言

AVL樹的特點

AVL樹的插入

節點的定義

情況分析

AVL樹的旋轉

右單旋

左單旋

左右雙旋

右左雙旋

?編輯總結?

驗證AVL樹

前言

二叉搜索樹可以幫助我們以極高的效率查找(理想情況下是logn)，但是當在極端情況下，比如當樹中的節點值是有序的時，二叉搜索樹會變成一個單枝樹，相當于一個鏈表，于是乎為了讓樹更接近與一個完全二叉樹，想著當向二叉搜索樹中插入新節點后，讓每個節點的左右子樹高度差的絕對值不超過1就可以降低樹的高度從而提高效率，于是就有了AVL樹。

AVL樹的特點

每個節點的左右子樹都是AVL樹
左右子樹高度差(平衡因子)的絕對值不超過1

AVL樹的插入

節點的定義

static class TreeNode {public int val;public TreeNode left;public TreeNode right;public int bf;//平衡因子public TreeNode parent;public TreeNode(int val) {this.val = val;}}

?//平衡因子=右子樹高度-左子樹高度

情況分析

因為AVL樹也是二叉搜索樹，所以先按照二叉搜索樹的方式插入一個節點cur，但是當cur被插入后，其父節點parent的平衡因子必定會發生變化(左右子樹高度差必定發生變化)，所以每次插入節點后都需要更新平衡因子，并且檢查AVL樹的結構是否被破壞。情況可以分為以下幾種

cur插入之前parent的平衡因子會有三種可能'-1' ,'0' ,'1'

當cur插入到parent的左邊時parent的平衡因子-1
當cur插入到parent的右邊時parent的平衡因子+1?

cur插入之后parent的平衡因子可能會有五種可能‘-1’，‘+1’，‘0’，‘-2’，‘+2’

?如果cur插入后parent的平衡因子是0，說明插入之前它的平衡因子是正負1，所以插入后才可能被調整為0，此時cur成功插入
如果cur插入后parent的平衡因子是正負1，說明插入之前它的平衡因子是0，所以插入后才可能被調整為正負1，此時以parent為根的樹高度增加了，上面節點的平衡因子可能會被打破所以需要繼續向上更新
如果cur插入后parent的平衡因子是正負2，則說明以parent為根的樹不符合AVL樹的性質，需要對其進行調整，既旋轉

插入節點

TreeNode node = new TreeNode(val);//如果根節點為空直接插入if (root == null) {root = node;return true;}TreeNode parent = null;TreeNode cur = root;while (cur != null) {if (val > cur.val) {parent = cur;cur = cur.right;} else if (val < cur.val) {parent = cur;cur = cur.left;} else {return false;}}//cur == nullif (val > parent.val) {parent.right = node;} else if (val < parent.val) {parent.left = node;}

調整parent的平衡因子

//調整cur = node;node.parent = parent;while (parent != null) {//如果cur是父節點的右孩子，父節點的平衡因子就加一，否則減一if (cur == parent.right) {parent.bf++;} else {parent.bf--;}//判斷平衡因子if (parent.bf == 0) {//已經平衡break;} else if (parent.bf == 1 || parent.bf == -1) {//繼續向上調整cur = parent;parent = cur.parent;} else {if (parent.bf == 2) {//右樹高，需要降低右樹高度(說明cur插到了parent的右邊)if (cur.bf == 1) {//左單旋} else if (cur.bf == -1) {//右左雙旋}//左樹高，需要降低左樹高度} else {//parent.bf == -2(說明cur插到了parent的左邊)if (cur.bf == -1) {//右單旋} else if (cur.bf == 1) {//左右雙旋}}break;}}

AVL樹的旋轉

右單旋

當新節點插入較高左子樹的左側

上圖是一個簡單的右旋，當新節點10插入到30的左子樹時(這里是左子樹)，破壞了avl樹的平衡節點50的平衡因子變成-2，表示左子樹比右子樹高2，所以我們需要降低左子樹，提高右子樹。既將50節點向右旋轉到30節點的左邊(因為50比三十大，只能在30的右邊)，此時這顆AVL樹就平衡了(別忘了修改平衡因子bf)

但是實際插入中的AVL樹的結構可能不會和上圖這樣簡單比如：

30的右邊可能已經有節點了

0是新插入的節點插到了30的左子樹的左側，破壞了AVL樹的平衡，使50節點的平衡因子變成-2，所以和剛剛一樣我們需要降低左樹，抬高右樹，我們讓50節點向右旋轉，但是此時30節點的右邊已經有了一個節點(也可能是30的右子樹的根)，不過這個節點一定是大于30小于50的，所以我們只需要將這個節點放到50節點的左邊，然后再將50節點放到30節點的右邊即可，最后修改平衡因子。

?50可能是其他節點的左右子樹或者根節點

?如果50是根節點那么當旋轉完成后要更新根節點，如果50是其父節點的左孩子，那么要讓30節點變成50原父節點的左孩子，右孩子則相反

代碼

public void rotateRight(TreeNode parent) {TreeNode pParetn = parent.parent;//記錄parent的父節點TreeNode subL = parent.left;//parent的左孩子TreeNode subLR = subL.right;//parent的左孩子的右孩子parent.left = subLR;if (subLR != null) {subLR.parent = parent;}subL.right = parent;parent.parent = subL;//檢查當前parent是不是根節點//是根節點的話直接讓subL為根節點if (parent == root) {root = subL;root.parent = null;} else {//不是根節點，就判斷parent是其父節點的左孩子還是右孩子if (parent == pParetn.left) {//parent是左孩子，就讓subL也是左孩子pParetn.left = subL;} else {pParetn.right = subL;}subL.parent = pParetn;}subL.bf = 0;parent.bf = 0;}

首先先標記右旋所需要的節點，然后開始右旋，過程和前文一樣

將subLR作為parent的左孩子(就算subLR為空也無所謂)
判斷subL是否有右孩子(subLR) ，有的話就令subLR的父節點位parent
讓subL的右節點為parent
讓parent的父節點為subLR
旋轉完成后判斷parent是否是根節點是的話，更新根節點，有父節點的話則讓subL為parent父節點的孩子
最后修改平衡因子

右旋代碼既圖解?

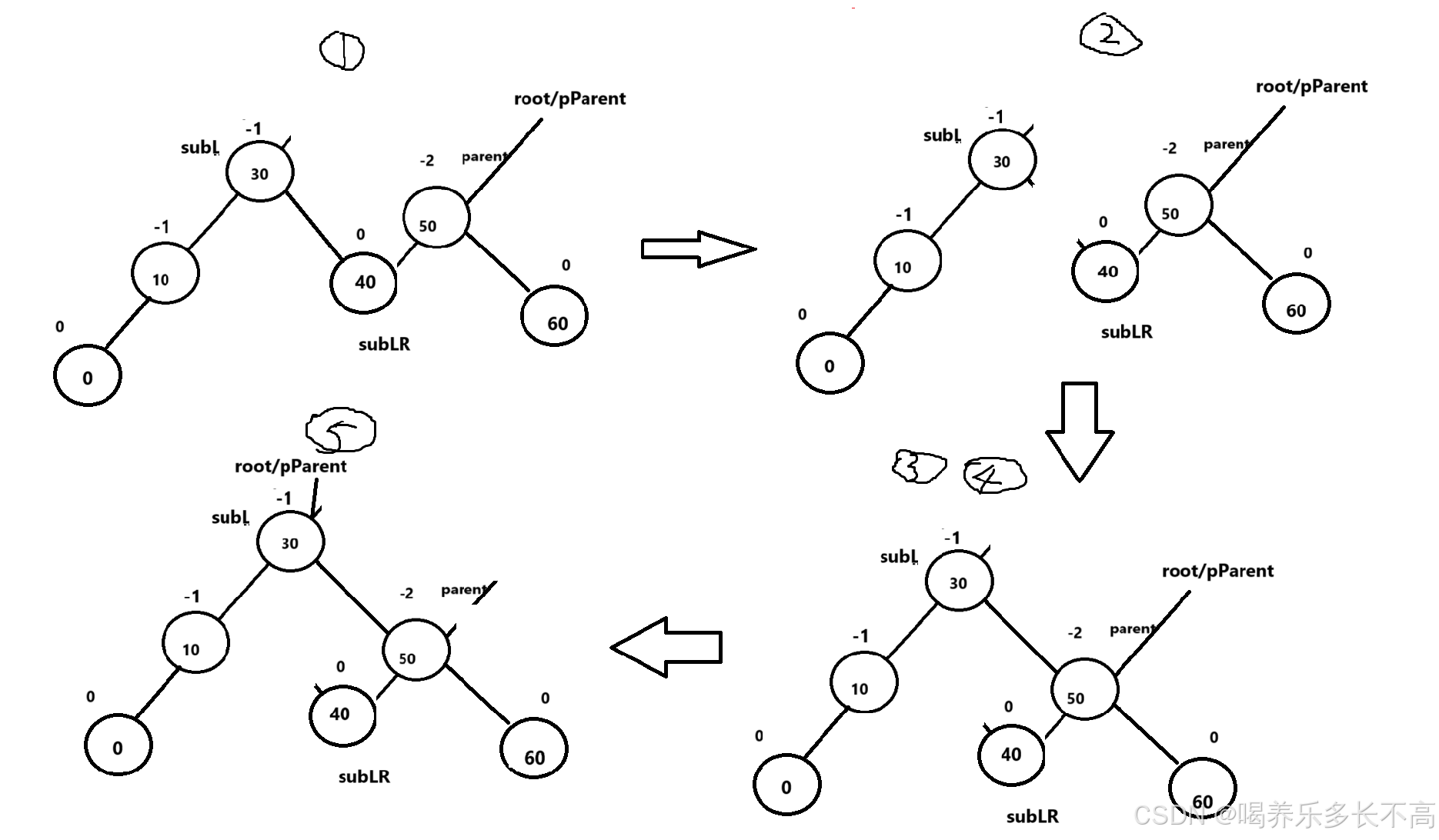
左單旋

當新節點插入較高右子樹的右側

左單旋的方法和右單旋一樣，只是方向不一樣，具體過程參考右單旋

代碼及圖解

private void rotateLeft(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;parent.right = subRL;subR.left = parent;if (subRL != null) {subRL.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subR;//檢查當前parent是不是rootif (parent == root) {root = subR;root.parent = null;} else {//不是rootif (pParent.right == parent) {pParent.right = subR;} else {pParent.left = subR;}subR.parent = pParent;}parent.bf = 0;subR.bf = 0;}

?左旋

首先先標記左旋所需要的節點，然后開始左旋
將subRL作為parent的右孩子
判斷subR的左孩子是否為空，如果不為空則令subR的左孩子(subRL)的父節點為parent
令subR的左孩子為parent
令parent的parent為subR
旋轉完成后判斷parent是否是根節點是的話，更新根節點，有父節點的話則讓subR為parent父節點的孩子
最后修改平衡因子

左右雙旋

新節點插入較高左子樹的右側

這種情況無法通過直接左旋或者右旋使樹平衡，需要先左旋再右旋，通過左旋把樹變成左子樹較高的情況然后再右旋

可以看到只是右旋達不到平衡的結果

先左旋再右旋

private void rotateLR(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;int bf = subLR.bf;rotateLeft(parent.left);rotateRight(parent);if (bf == 1) {subL.bf = 0;subLR.bf = 0;parent.bf = 1;} else if (bf == -1) {subL.bf = -1;subLR.bf = 0;parent.bf = 0;}}

?以上面的例子說明當bf==1時說明新節點插到45左邊，bf==-1時說明新節點插到45右邊

bf==-1時旋轉結果

右左雙旋

新節點插到較高右子樹的左側

private void rotateRL(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;int bf = subRL.bf;rotateRight(parent.right);rotateLeft(parent);if (bf == 1) {parent.bf = -1;subR.bf = 0;subRL.bf = 0;} else if (bf == -1) {parent.bf = 0;subR.bf = 1;subRL.bf = 0;}}

總結?

當新節點插入后如果樹不平衡，既parent的平衡因子為-2或者2

1.parent的平衡因子為2，說明右樹高

如果SubR(右子樹)的平衡因子為1，說明新節點插入較高右子樹的右側，執行左單旋
如果SubR的平衡因子為-1，說明新節點插入到較高右子樹的左側，執行右左雙旋

2.parent的平衡因子為-2，說明左樹高

如果SubL的平衡因子為-1，說明新節點插入到了較高左子樹的左邊，執行有右選
如果SubL的平衡因子為1，說明新節點插入到了較高左子樹的右邊，執行左右雙旋?

驗證AVL樹

驗證AVL樹只需要判斷每個節點的左右子樹高度差的絕對值都小于一就行

public int height(TreeNode node) {if (node == null) {return 0;}int left = height(node.left);int right = height(node.right);return left > right ? left + 1 : right + 1;}public Boolean isbalanced(TreeNode root) {if (root == null) {return true;}//求左右子樹高度int left = height(root.left);int right = height(root.right);if (root.bf != right - left) {return false;}return Math.abs(left - right) <= 1&& isbalanced(root.left)&& isbalanced(root.right);}public static void main(String[] args) {int[] array = {17, 4, 8, 6, 17, 25, 17, 19, 10};AVLTree avlTree = new AVLTree();for (int i=0;i<array.length;++i){avlTree.insert(array[i]);}boolean ret = avlTree.isbalanced(avlTree.root);System.out.println(ret);}

綜上，AVL樹其實就是一個相對平衡的二叉搜索樹，每個節點的左右子樹高度差的絕對值都小于一，這樣可以使其查找的時間復雜度穩定為O(logN)，但是也因為其在進行修改操作時比如插入刪除，需要對樹進行多次旋轉，使其修改變得及其麻煩。所以，如果需要一種查詢高效且有序的數據結構，而且數據的個數為靜態的(修改操作較少或不修改)，可以考慮AVL樹，但一個結構經常修改，就不太適合

以上就是博主對AVL樹知識的分享，在之后的博客中會陸續分享有關數據結構的其他知識，如果有不懂的或者有其他見解的歡迎在下方評論或者私信博主，也希望可以多多支持博主！！🥰🥰