【機器學習】樸素貝葉斯

一、樸素貝葉斯的算法原理

1.1 定義

1.2 貝葉斯定理

1.3?條件獨立性假設

二、樸素貝葉斯算法的幾種常見類型

2.1??高斯樸素貝葉斯 (Gaussian Naive Bayes)

【訓練階段】 - 從數據中學習模型參數

【預測階段】 - 對新樣本 Xnew? 進行分類

2. 2 多項式樸素貝葉斯 (Multinomial Naive Bayes)

【訓練階段】 - 學習模型參數

【預測階段】 - 對新樣本 Xnew? 進行分類

2.3 伯努利樸素貝葉斯 (Bernoulli Naive Bayes)

【訓練階段】 - 學習模型參數

【預測階段】 - 對新樣本 Xnew? 進行分類

三、實例：基于樸素貝葉斯的好瓜預測

任務：對一個給定的西瓜樣本進行二分類（好瓜/壞瓜）

1.訓練數據

2.測試數據

3.計算步驟

4.代碼實現

四、學習總結

一、樸素貝葉斯的算法原理

1.1 定義

樸素貝葉斯是一種基于 貝葉斯定理 的 概率分類算法。它屬于 監督學習 算法的一種，也就是說，它需要一個帶有標簽（即正確答案）的訓練數據集來學習。

它的核心思想是：對于一個未知類別的數據樣本，計算該樣本 屬于各個類別的概率，然后選擇 概率最大的那個類別 作為它的預測類別。

1.2 貝葉斯定理

貝葉斯定理描述了在已知某些條件下，一個事件發生的概率。

在分類問題中，我們想知道的是：在看到了某個數據樣本的特征（X）之后，這個樣本屬于某個類別（y）的概率是多少？

這個概率被稱為 后驗概率 (Posterior Probability)，用數學公式表示就是 P(y∣X)。

貝葉斯定理的公式如下：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? $P(y|X) = \frac{P(X|y)P(y)}{P(X)}$

其中

P(y∣X): 后驗概率 (Posterior Probability)

P(X∣y): 似然性 (Likelihood)

在 假設樣本屬于類別 y 的前提下，觀察到特征數據 X 的概率。

P(y): 先驗概率 (Prior Probability)

在 觀察到任何特征數據 X 之前，認為樣本屬于類別 y 的概率。

P(X): 證據 (Evidence)

觀察到特征 X 的概率。這是一個歸一化因子，確保所有類別的后驗概率加起來等于1。在分類任務中，對于所有類別，P(X) 的值都是相同的。因此，在比較不同類別的后驗概率 P(y∣X) 時，我們 只需要比較分子 P(X∣y)P(y) 的大小即可，可以忽略分母 P(X)。

所以，我們的目標簡化為：計算每個類別 y 的 P(X∣y)P(y) 值，哪個類別的這個值最大，就預測樣本屬于哪個類別。

1.3?條件獨立性假設

計算似然性 P(X∣y) 看似簡單，但 X 通常包含多個特征 (x1?,x2?,...,xn?)。

直接計算 P(x1?,x2?,...,xn?∣y) 是非常困難的，因為它需要考慮所有特征之間的復雜聯合關系，這需要極大的數據集才能準確估計。

為了簡化計算，“樸素”貝葉斯算法引入了一個關鍵的假設：

給定類別 y 的條件下，所有特征 X=(x1?,x2?,...,xn?) 之間是相互條件獨立的?

這意味著：

? ? ? ? ? ? ? ? ? $P(X|y)=P(x_{1},x_{2},...,x_{n}|y)\approx P(x_{1}|y)\times P(x_{2}|y)\times...\times P(x_{n}|y)$

二、樸素貝葉斯算法的幾種常見類型

樸素貝葉斯算法的核心思想基于?貝葉斯定理?和 特征條件獨立性假設 。

不同的樸素貝葉斯變體主要是因為它們對 特征數據的概率分布 P(xi?∣y) 做出了不同的假設。

根據特征數據類型的不同，最常見的樸素貝葉斯分類器有以下三種：

高斯樸素貝葉斯 (Gaussian Naive Bayes)
多項式樸素貝葉斯 (Multinomial Naive Bayes)
伯努利樸素貝葉斯 (Bernoulli Naive Bayes)

2.1??高斯樸素貝葉斯 (Gaussian Naive Bayes)

主要用于處理 連續型特征

【訓練階段】 - 從數據中學習模型參數

1.計算先驗概率 P(y)

統計訓練數據中每個類別 y出現了多少次。
用每個類別的樣本數除以總樣本數，得到該類別的先驗概率。
公式：

2.按類別分組數據

?將訓練數據按照類別標簽分開，方便后續計算。

3.計算每個類別下每個特征的均值 μy,i? 和標準差 σy,i?

對每一個類別 y：

對該類別下的每一個連續特征 xi?：
- 計算這個特征在 只屬于類別 y 的樣本 中的 平均值 μy,i?
- 計算這個特征在 只屬于類別 y 的樣本 中的 標準差 σy,i

?4.處理零標準差情況

如果在某個類別 y 下，某個特征 xi? 的所有值都完全相同，那么計算出的標準差 σy,i? 會是 0。這在后續計算高斯概率密度時會導致除零錯誤。
解決方法： 檢查是否有 σy,i?=0 的情況。如果存在，將其替換為一個非常小的正數，或者使用更復雜的方差平滑技術。

5.存儲模型參數

保存好計算出的所有類別的先驗概率 P(y)，以及每個類別下每個特征的均值 μy,i? 和（處理過的）標準差 σy,i?。

【預測階段】 - 對新樣本 Xnew? 進行分類

假設新樣本 Xnew? 包含特征值 (x1?,x2?,...,xn?)

1.為每個可能的類別 y 計算得分

初始化得分： 通常取先驗概率的對數：?

累加特征的對數似然： 對于新樣本中的 每一個連續特征 xi?：

取出訓練階段為類別 y 和特征 i 存儲的均值 μy,i? 和標準差 σy,i?。
使用 高斯概率密度函數 (PDF) 公式 計算該特征值 xi? 在類別 y 模型下的概率密度：

將計算得到的 logPDF(xi?∣y) 加到對應類別 y 的得分上：

2.比較得分并預測

對所有可能的類別 y 都執行完步驟 1 后，比較它們最終的 Score
得分最高的那個類別，就是高斯樸素貝葉斯對新樣本 Xnew? 的預測結果。

2. 2 多項式樸素貝葉斯 (Multinomial Naive Bayes)

特征是離散的，通常表示某件事發生的次數或頻率

【訓練階段】 - 學習模型參數

1.計算先驗概率 P(y)

同高斯樸素貝葉斯

2.按類別分組數據

同高斯樸素貝葉斯

3.統計特征計數 Nyi? 和總計數 Ny?

確定整個數據集的 特征詞匯表（所有出現過的不同特征/單詞）。

設詞匯表大小（或總特征數）為 k。

對每一個類別 y：

計算 Ny?：該類別下 所有樣本 中，所有特征 出現的 總次數 之和。
對詞匯表中的每一個特征 xi?：
- 計算 Nyi?：該類別下 所有樣本 中，特征 xi? 出現的 總次數。

4.選擇平滑參數 α

通常使用拉普拉斯平滑，即 α=1

5.存儲模型參數

?保存先驗概率 P(y)，所有類別的總特征數 Ny?，每個類別下每個特征的計數 Nyi?，以及詞匯表大小 k 和平滑參數 α。

【預測階段】 - 對新樣本 Xnew? 進行分類

假設新樣本 Xnew? 由特征計數 (count(x1?),count(x2?),...,count(xk?)) 表示，其中 count(xi?) 是特征 i 在 Xnew? 中出現的次數。

1.為每個可能的類別 y 計算得分

初始化得分：

累加特征的對數似然： 對于詞匯表中的 每一個特征 xi? (從 i=1 到 k)：

取出訓練階段為類別 y 存儲的 Nyi?, Ny?
使用 平滑公式計算條件概率 P(xi?∣y)：

? ? ? ? ? ? ? ? ? ? ? ? ? ?

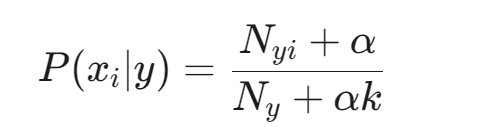
獲取該特征 xi? 在 新樣本 Xnew? 中的計數 count(xi?)。
將該特征對得分的貢獻（其計數值乘以其對數概率）累加到對應類別 y 的得分上：

這里體現了出現次數越多的特征，對總得分的影響越大

2.比較得分并預測

比較所有類別的最終 Score
得分最高的類別即為預測結果。

2.3 伯努利樸素貝葉斯 (Bernoulli Naive Bayes)

特征是二元的（0/1），表示某事物是否存在、發生與否。

【訓練階段】 - 學習模型參數

1.計算先驗概率 P(y)

同高斯樸素貝葉斯。

2.按類別分組數據

同高斯樸素貝葉斯。

3.統計特征出現次數 Ny,xi?=1? 和類別總數 Ny?

確定所有可能的二元特征列表

對每一個類別 y：

計算 Ny?：屬于該類別的 樣本總數

對每一個特征 xi?:?

計算 Ny,xi?=1?：在類別 y 的樣本中，特征 xi? 出現過（值為1）的樣本數量。

4.選擇平滑參數 α

通常 α=1

5.存儲模型參數

?保存先驗概率 P(y)，每個類別下每個特征的出現次數 Ny,xi?=1?，以及每個類別的總樣本數 Ny?

【預測階段】 - 對新樣本 Xnew? 進行分類

假設新樣本 Xnew? 由二元特征向量 (x1?,x2?,...,xk?) 表示，其中 xi?∈{0,1}。

1.為每個可能的類別 y 計算得分

初始化得分：

累加特征的對數似然： 對于 每一個特征 xi? (從 i=1 到 k)：

取出訓練階段為類別 y 存儲的 Ny,xi?=1? 和 Ny?

計算特征 i 在類別 y 下出現的概率 P(xi?=1∣y):

計算特征 i 在類別 y 下不出現的概率 P(xi?=0∣y)

根據新樣本 Xnew? 中特征 xi? 的值，選擇對應的概率并累加其對數：

如果 Xnew? 中 xi?=1（特征出現），則? ${Score}_y = \text{Score}_y + \log P(x_i = 1|y)$
如果 Xnew? 中 xi?=0（特征未出現），則 ${Score}_y = \text{Score}_y + \log P(x_i = 0|y)$

2.比較得分并預測

比較所有類別的最終 Score?
得分最高的類別即為預測結果

三、實例：基于樸素貝葉斯的好瓜預測

目標是根據一系列已知特征，判斷一個西瓜是“好瓜”（標記為“是”）還是“壞瓜”（標記為“否”）。

任務：對一個給定的西瓜樣本進行二分類（好瓜/壞瓜）

1.訓練數據

數據集摘要:

總樣本數: 17
好瓜 (是) 數量: 8
壞瓜 (否) 數量: 9

2.測試數據

3.計算步驟

使用拉普拉斯平滑和高斯分布假設，方差使用N作為分母

計算后驗概率

比較結果

計算出的 "好瓜=是" 的得分 (0.02177) 遠大于 "好瓜=否" 的得分 (0.000036)

結論

根據樸素貝葉斯分類器的計算結果，對于測試樣本 "測1"（特征為青綠, 蜷縮, 濁響, 清晰, 凹陷, 硬滑, 密度=0.697, 含糖率=0.460），預測結果為 是 (好瓜)。

4.代碼實現

import pandas as pd
import math# 1. 數據準備 
data = {'色澤': ['青綠', '烏黑', '烏黑', '青綠', '淺白', '青綠', '烏黑', '烏黑', '烏黑', '青綠', '淺白', '淺白', '青綠', '淺白', '烏黑', '淺白', '青綠'],'根蒂': ['蜷縮', '蜷縮', '蜷縮', '蜷縮', '蜷縮', '稍蜷', '稍蜷', '稍蜷', '稍蜷', '硬挺', '硬挺', '蜷縮', '稍蜷', '稍蜷', '稍蜷', '蜷縮', '蜷縮'],'敲聲': ['濁響', '沉悶', '濁響', '沉悶', '濁響', '濁響', '濁響', '濁響', '沉悶', '清脆', '清脆', '濁響', '濁響', '沉悶', '濁響', '濁響', '沉悶'],'紋理': ['清晰', '清晰', '清晰', '清晰', '清晰', '清晰', '稍糊', '清晰', '稍糊', '清晰', '模糊', '模糊', '稍糊', '稍糊', '清晰', '模糊', '稍糊'],'臍部': ['凹陷', '凹陷', '凹陷', '凹陷', '凹陷', '稍凹', '稍凹', '稍凹', '稍凹', '平坦', '平坦', '平坦', '凹陷', '凹陷', '稍凹', '平坦', '稍凹'],'觸感': ['硬滑', '硬滑', '硬滑', '硬滑', '硬滑', '軟粘', '軟粘', '硬滑', '硬滑', '軟粘', '軟粘', '硬滑', '軟粘', '硬滑', '軟粘', '硬滑', '硬滑'],'密度': [0.697, 0.774, 0.634, 0.608, 0.556, 0.403, 0.481, 0.437, 0.666, 0.243, 0.245, 0.343, 0.639, 0.657, 0.360, 0.593, 0.719],'含糖率': [0.460, 0.376, 0.264, 0.318, 0.215, 0.237, 0.149, 0.211, 0.091, 0.267, 0.057, 0.099, 0.161, 0.198, 0.370, 0.042, 0.103],'好瓜': ['是', '是', '是', '是', '是', '是', '是', '是', '否', '否', '否', '否', '否', '否', '否', '否', '否']
}
df = pd.DataFrame(data)# 定義離散和連續特征列名
discrete_cols = ['色澤', '根蒂', '敲聲', '紋理', '臍部', '觸感']
continuous_cols = ['密度', '含糖率']
target_col = '好瓜'# 2. 訓練模型
# 計算先驗概率 P(y)
prior_prob = df[target_col].value_counts(normalize=True).to_dict()# 計算離散特征的條件概率 P(xi|y) - 使用拉普拉斯平滑
cond_prob_discrete = {}
for feature in discrete_cols:cond_prob_discrete[feature] = {}# 獲取該特征的所有可能取值possible_values = df[feature].unique()k = len(possible_values) for value in possible_values:cond_prob_discrete[feature][value] = {}for class_label in df[target_col].unique():# 獲取目標類別的數據子集class_subset = df[df[target_col] == class_label]# 計算分子：(類別為y且特征為x的數量 + 1)count_feature_class = class_subset[class_subset[feature] == value].shape[0] + 1# 計算分母：(類別為y的數量 + k)count_class = class_subset.shape[0] + kcond_prob_discrete[feature][value][class_label] = count_feature_class / count_class# 計算連續特征的均值和標準差，按類別分組
mean_std_continuous = {}
for feature in continuous_cols:mean_std_continuous[feature] = {}for class_label in df[target_col].unique():class_subset = df[df[target_col] == class_label]# 計算均值和標準差 (使用 N-1 作為分母，即樣本標準差)mean = class_subset[feature].mean()std = class_subset[feature].std()# 防止標準差為0 (如果某類下某個連續特征值都一樣)if std == 0:std = 1e-6 mean_std_continuous[feature][class_label] = {'mean': mean, 'std': std}# 高斯概率密度函數
def gaussian_pdf(x, mean, std):exponent = math.exp(-((x - mean) ** 2 / (2 * std ** 2)))return (1 / (math.sqrt(2 * math.pi) * std)) * exponent# 3. 預測函數 (Prediction Function)
def predict_watermelon(test_data):scores = {}# 遍歷每個類別 ('是', '否')for class_label in prior_prob.keys():# 初始化得分為該類別的先驗概率 P(y)score = math.log(prior_prob[class_label])# 計算離散特征的條件概率連乘 (對數形式下為連加)for feature in discrete_cols:value = test_data[feature]if value in cond_prob_discrete[feature]:score += math.log(cond_prob_discrete[feature][value][class_label])else:score += math.log(1e-9) # 計算連續特征的高斯概率密度連乘 (對數形式下為連加)for feature in continuous_cols:x = test_data[feature]stats = mean_std_continuous[feature][class_label]pdf = gaussian_pdf(x, stats['mean'], stats['std'])if pdf > 0:score += math.log(pdf)else:score += math.log(1e-9)scores[class_label] = score# 返回得分最高的類別prediction = max(scores, key=scores.get)return prediction, scores# 4. 進行預測 
test_sample = {'色澤': '青綠','根蒂': '蜷縮','敲聲': '濁響','紋理': '清晰','臍部': '凹陷','觸感': '硬滑','密度': 0.697,'含糖率': 0.460
}# 調用預測函數
prediction, scores = predict_watermelon(test_sample)print(f"\n測試樣本: {test_sample}")
print(f"預測結果: {prediction}")
print(f"各類別的對數得分: {scores}")