1、具有5個頂點的有向完全圖有20條弧。

2、若一個有向圖用鄰接矩陣表示，則第個結點的入度就是：第i列的非零元素的個數。

3、有向圖的鄰接矩陣可以是對稱的，也可以是不對稱的。

4、設N個頂點E條邊的圖用鄰接表存儲，則求每個頂點入度的時間復雜度為：O(N+E)。

5、在一個有向圖中，所有頂點的入度與出度之和等于所有邊之和的2倍。

6、如果G是一個有28條邊的非連通無向圖，那么該圖頂點個數最少為9.

7、下面給出的有向圖中，各個頂點的入度和出度分別是：入度: 0, 2, 3, 1, 2; 出度: 3, 2, 1, 1, 1

8、給定一個有向圖的鄰接表如下圖，則該圖有3 {{2}, {4}, {0, 1, 3, 5}}個強連通分量

9、

給定有向圖的鄰接矩陣如下：

頂點2（編號從0開始）的出度和入度分別是：0,2.

10、設無向圖為 G=(V，E)，其中 V={v1,v2,v3,v4}，E={(v1,v2)，(v3,v4)，(v4,v1)，(v2,v3)，(v1,v3)}。則每個頂點的度依次為：3,2,3,2.

11、對于給定的有向圖如下，其鄰接矩陣為：

12、對于給定的有向圖如下，其逆鄰接表為：

13、以下哪個是給定無向帶權圖的鄰接矩陣

14、圖的遍歷是從給定的源點出發每一個頂點僅被訪問一次。

15、遍歷的基本算法有兩種：深度遍歷和廣度遍歷。

16、圖的深度遍歷是一個遞歸過程。

17、已知一個圖的鄰接矩陣如下，則從頂點V1出發按深度優先搜索法進行遍歷，可能得到的一種頂點序列為1,V2,V4,V5,V6,V3

18、給定一有向圖的鄰接表如下。從頂點V1出發按深度優先搜索法進行遍歷，則得到的一種頂點序列為：V1,V5,V4,V7,V6,V3,V2

19、在圖中自c點開始進行廣度優先遍歷算法可能得到的結果為c,f,a,d,e,b

20、給定一有向圖的鄰接表如下。從頂點V1出發按廣度優先搜索法進行遍歷，則得到的一種頂點序列為：V1,V3,V2,V4,V5

21、已知一個圖的鄰接矩陣如下，則從頂點V1出發按廣度優先搜索法進行遍歷，可能得到的一種頂點序列為：V1,V2,V3,V5,V4,V6

22、對下圖從頂點C出發進行廣度優先搜索CBDAEHFG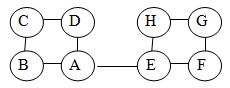

23、已知無向圖G含有16條邊，其中度為4的頂點個數為3，度為3的頂點個數為4，其他頂點的度均小于3。圖G所含的頂點個數至少是11.

24、對于無向圖G=(V,E) ,當|V|>|E|+1?時，G一定不是連通的。

25、若無向圖 G=(V,E) 的鄰接多重表如下圖所示，則 G 中頂點 b 與 d 的度分別是2,4

26、修改遞歸方式實現的圖的深度優先搜索（DFS）算法，將輸出（訪問）頂點信息的語句移動到退出遞歸前（即執行輸出語句后立即退出遞歸）。采用修改后的算法遍歷有向無環圖 ，若輸出結果中包含 ?中的全部頂點，則輸出的頂點序列是 ?的逆拓撲有序序列。

27、