基本定位:
適用于解決評價,選擇類問題(數值不確定,需要自己結合資料數據等自己填寫)。
引入:
若要解決選擇類的問題,打分的方式最為常用——即采用權重表:
| 指標權重 | 選擇1 | 選擇2 | ........ | |
| 指標1 | ||||
| 指標2 | ||||
| 指標3 | ||||
| ........ |
各指標權重之和為1,各方案在某指標上的打分之和也應為1.?
那么我們來看一道例題:
A想去旅游,在查閱網上攻略后,初步選擇了蘇杭,北戴河,桂林三地之一作為目標景點。
請你確定評價指標,形成評價體系來為小明同學選擇最佳的方案:
?評價類問題的入手思路:
1,我們評價的目標是什么?
2,我們為了達成這個目標,有哪幾種方案?
3,評價的標準或者說指標是什么?
在本題中:
1,為A 找到最佳的景點。
2,三地。
3,答案常常需要根據題目的背景資料,常識,網上搜集的資料進行結合,篩選出最合適的指標
網上資料搜索推薦:
1,知網——引用論文,同時學習分析方法
2,https://search.chongbuluo.com/
那么假設現在已經找到了以下五個指標:
景色,花費,居住,飲食,交通;
列出權重表:
| 指標權重 | 蘇杭 | 北戴河 | 桂林 | |
| 景色 | ||||
| 花費 | ||||
| 居住 | ||||
| 飲食 | ||||
| 交通 |
那么剩下的就是找到各指標的權重大小:
問題——當分析多因素對于某一問題的影響大小時,單獨分析某一個因素的影響可能會有失偏頗
解決方法:
采用分而治之的思想——要求被分析對象兩兩指標之間進行比較,根據最終的比較結果來推算權重
——這就是層次分析法的思想。?
層次分析法的思想:
| 標度 | 含義 |
| 1 | 表示兩個因素相比,同等重要 |
| 3 | 表示兩個因素相比,一個因素比另一個稍微重要 |
| 5 | 表示兩因素相比,一個因素比另一個明顯重要 |
| 7 | 表示兩因素相比,一個因素比另一個強烈重要 |
| 9 | 表示兩因素相比,一個因素比另一個極端重要 |
| 2,4,6,8 | 表示相鄰判斷之間的中值 |
| 倒數 | 若A比B標度為3,則B比A標度為1/3 |
| 景色 | 花費 | 居住 | 飲食 | 交通 | |
| 景色 | 1 | 1/2 | 4 | 3 | 3 |
| 花費 | 2 | 1 | 7 | 5 | 5 |
| 居住 | 1/4 | 1/7 | 1 | 1/2 | 1/3 |
| 飲食 | 1/3 | 1/5 | 2 | 1 | 1 |
| 交通 | 1/3 | 1/5 | 3 | 1 | 1 |
?總結:
上面的表格為一個5 X 5 的矩陣,即為A,對應元素即為. 具有如下特點:
1,表示的是與指標j相比,指標i的重要程度。
2,滿足(稱該矩陣為正互反矩陣)
上述矩陣即為層次分析法中的判斷矩陣
同樣方法也能用判斷矩陣得到各個方案對于某一因素的權重大小
PS:一個可能出現矛盾的地方:
例如:
蘇杭 = A, 北戴河 = B,桂林 = C;
蘇杭比北戴河景色好一點:A >?B; 蘇杭和桂林景色一樣好:A = C;
北戴河比桂林景色好一點:B > C;
此種情況應如何解決?
首先引入一致矩陣的概念:
一致矩陣:
若所構造的判斷矩陣滿足,則稱其為一致矩陣。
滿足——各行(列)之間成倍數關系
我們在使用判斷矩陣求權重之前,就必須對其進行一致性檢驗。
進行一致性檢驗的意義:
可能存在的問題:
例如:
設定蘇杭 = A,北戴河 = B,桂林 = C;
蘇杭比北戴河景色好一點:A > B;? ?蘇杭和桂林景色一樣好: A = C;
北戴河比桂林景色好一點: B > C;
此類題中出現了前后相矛盾的情況
故一致性檢驗的目的:為了檢驗我們構造的判斷矩陣和一致矩陣是否有太大的區別
引理基礎:
1,A為n階矩陣,且r(A) = 1,則A有一個特征值tr(A),其余特征值均為0;
? ? ?因為一致矩陣的各行成比例,故矩陣的秩一定為1,有一個特征值為n,其余特征值均為0;
2,n階正互反矩陣A為一致矩陣時,當且僅當最大特征值 = n;
? ? 當n階正互反矩陣A非一致時,一定滿足最大特征值 > n;
? ? 判斷矩陣越不一致,最大特征值與n相差越大;
一致性檢驗的步驟:
1,計算一致性指標CI;
2,查找對應的平均隨機一致性指標RI:
用隨機方法構造500個樣本矩陣,并隨機地從1~9及其倒數中抽取數字構造正互反矩陣,求得最大特征根的平均值D,并定義:
3,計算一致性比例CR:
?若CR < 0.1,則可認為判斷矩陣的一致性可以接受;否則需要對判斷矩陣進行修正
判斷矩陣怎么計算權重:
若我們所構造的判斷矩陣已通過一致性檢驗。
法1(算術平均法):
| 景色 | 蘇杭 | 北戴河 | 桂林 |
| 蘇杭 | 1 | 2 | 4 |
| 北戴河 | 1/2 | 1 | 2 |
| 桂林 | 1/4 | 1/2 | 1 |
?注意:權重最終值一定要進行歸一化處理。
蘇杭 = 1 / (1 / 2 + 1 + 1/ 4)
北戴河 = 1/2? / ( 1 + 1 / 2 + 1 / 4)
桂林 = 1 / 4 / (1 +1 / 2 +1 / 4 )
形似的,對于存在著誤差的判斷矩陣,
進行相同處理,對于每一列的計算結果,其答案有可能均不相同,那么判斷矩陣的計算結果即為n列結果的平均值。(算數平均法)
故按算術平均法計算權重步驟如下:
1,將判斷矩陣進行歸一化(每一個元素除以所在列的的和)
2,將歸一化的各列相加(按行求和)
3,將相加后得到的向量中每一個指標除以總列數后,即可得到權重向量;
法二,特征值法求權重:(最常用)
一致矩陣有一個特征值n,其余特征值均為0,。另外,特征值為n時,對應的特征向量剛好為
?又因為對于一致矩陣,1 / a1n? = an1;,即特征向量即是一致矩陣的第一列。
若判斷矩陣的一致性檢驗結果可以接受,那么就可以仿照一致矩陣的計算方法。
第一步:求出矩陣A的最大特征值及其對應的特征向量。
第二步:對求出的特征向量進行歸一化處理后即可得到權重
對于最終結果的處理:
?推薦使用EXCEL表格快速計算表格結果。
要點:通過F4鎖定單元格進行相同運算。
層次分析法:
一,畫出層次分析圖
分析系統中個元素之間的關系,建立系統的遞階層次結構
(注意:若使用了層次分析法,那么層次分析圖要放在建模論文中)
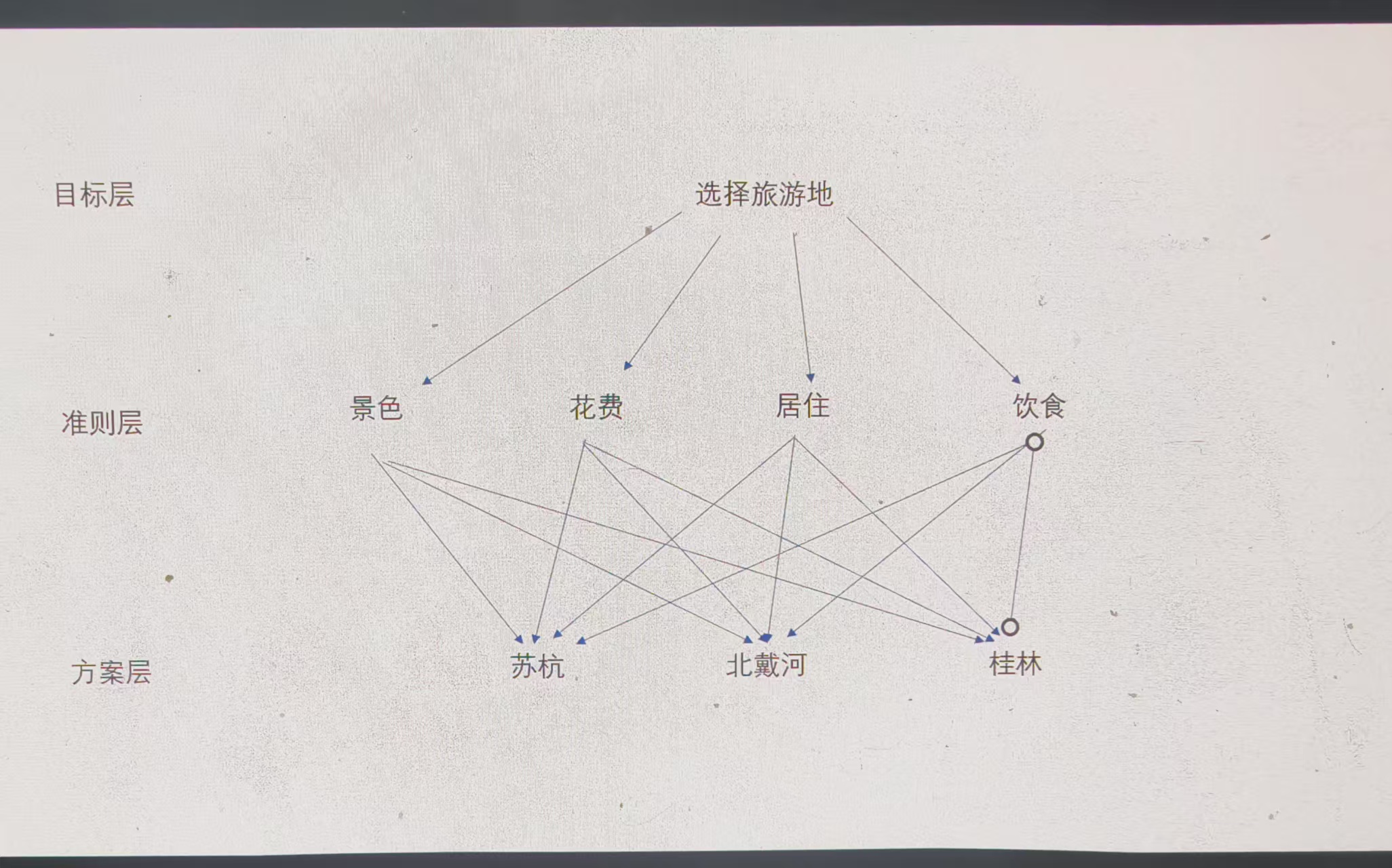
?二,構造判斷矩陣:
三,由判斷矩陣計算被比較元素的相對權重,并進行一致性判斷(檢驗通過才能使用權重):
? ? ? ?三種方法:
? ? ? ?1,算術平均法; 2,幾何平均法;? 3,特征值法;
?推薦比賽時,三種方法都使用。
在結論時便可加上——“為了保證結果的穩健性,本文采用了三種方法計算權重。再根據得到的權重矩陣計算各方案的得分,并進行排序和綜合分析。這樣避免了采用單一方法產生的偏差,得到的結論更全面,更有效”
若一致性檢驗結果? > 0.1:盡量往一致性矩陣方向靠攏(各行各列均成倍數)
四,運用EXCEL 表格對計算數值,并將結果進行排序
層次分析法的局限性:
一,評價的決策層不能太多:
一是判斷矩陣會與一致矩陣的差異很大;
二是平均隨機一致性指標RI的表格中n最多是15;
二,若決策層中指標的數值已知,那么我們若再使用自己填寫的判斷矩陣,則會加大誤差,所以此情況不能使用層次分析法。
模型拓展:
(1)決策層可以有多層,如子決策層,子子決策層.......
(2)一個決策可以只對應部分的方案,只需要在判斷矩陣中將相應的方案權重設為0即可
)


)




)










