查找技術（Searching Techniques）

---

查找簡介

在計算機科學中，“查找”指的是在某個集合或序列中尋找特定元素的過程。這個過程可以是成功的，也可以是失敗的：

• 若目標元素存在于集合中，我們稱之為“查找成功”，并返回它在集合中的位置；
• 若元素不存在，則稱為“查找失敗”。

查找是數據處理中的基本操作之一，幾乎出現在所有軟件系統的核心邏輯中。比如搜索聯系人、檢索圖書、匹配登錄密碼等，背后都離不開查找算法。

而不同的查找算法之間最大的差異，通常體現在“查找的效率”上。這個效率，很大程度上依賴于數據本身的“排列方式”——是否已排序。因此，我們在選擇查找方法時，必須考慮數據的特征。

---

本章將介紹兩種最基礎的查找技術：

1. 線性查找（Linear Search）

又名“順序查找”，是最直觀的查找方式。算法從第一個元素開始，依次與目標值進行比較，直到找到為止，或遍歷完所有元素。

這種方法的優勢是實現簡單，不要求數據有序；缺點是效率較低，特別是在數據量大的時候。

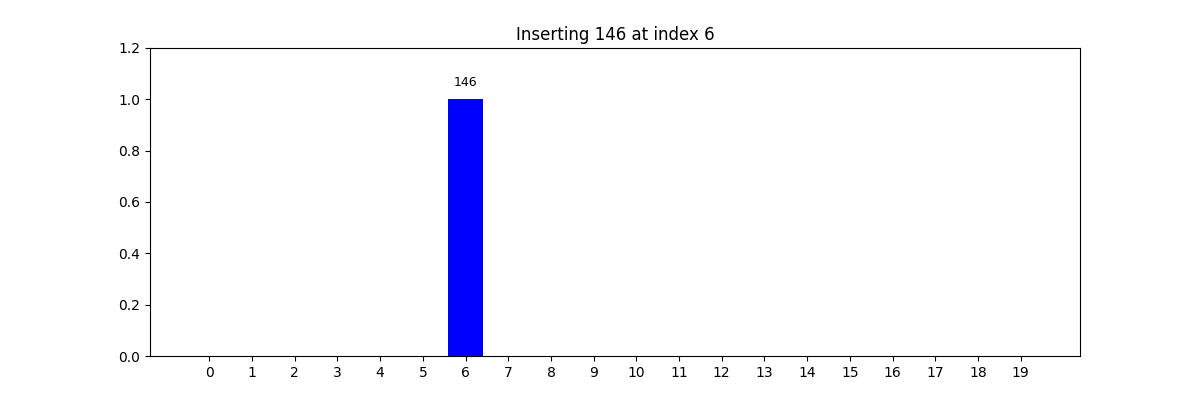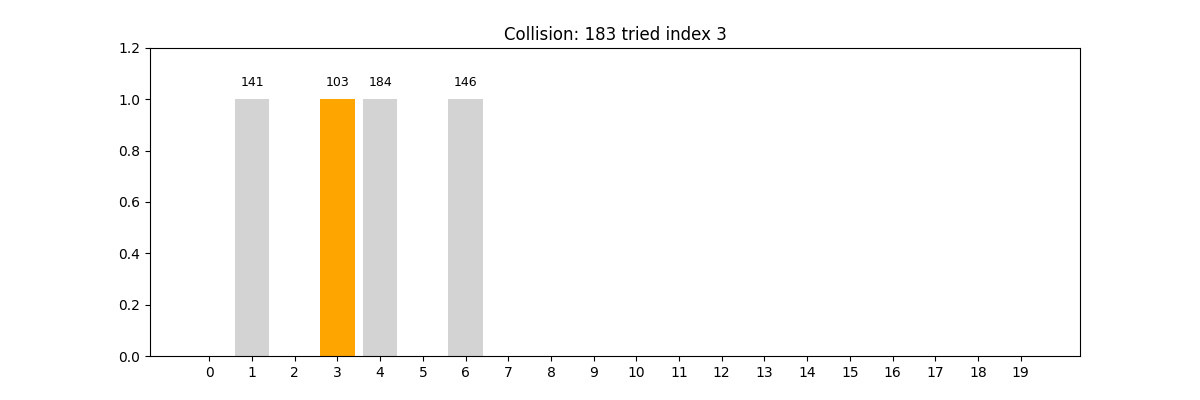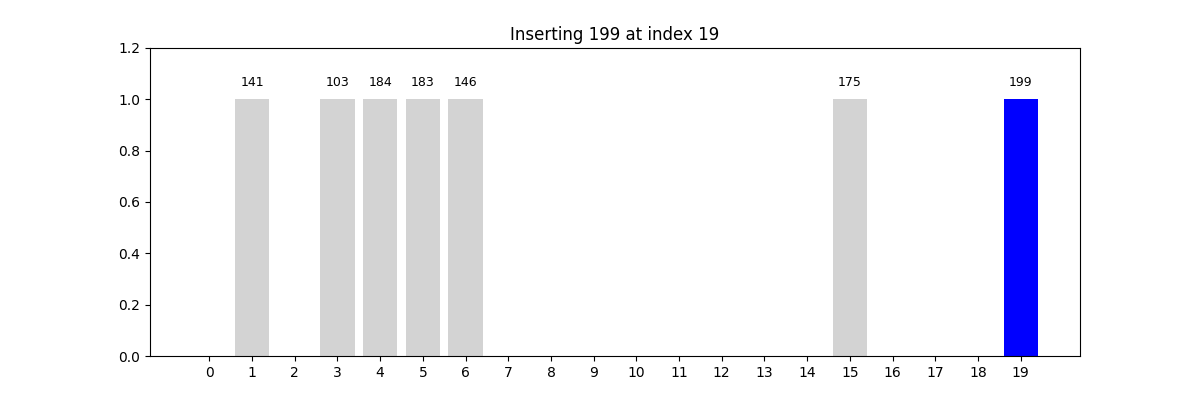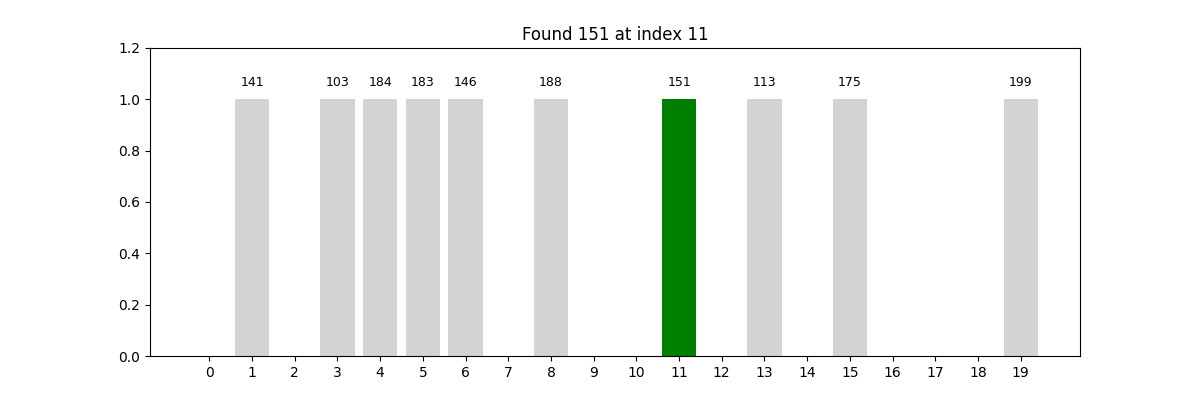
一個類比：想象你正在翻找一個裝滿撲克牌的盒子，想找一張紅桃 7。如果這些牌是雜亂無章地放著的，你只能一張張翻閱，直到找到為止——這就是線性查找的過程。

def linear_search(arr, target):steps = []  # 每一步的狀態for i in range(len(arr)):status = {'array': arr.copy(),'index': i,'found': arr[i] == target}steps.append(status)if arr[i] == target:break  # 找到目標值就提前退出return steps

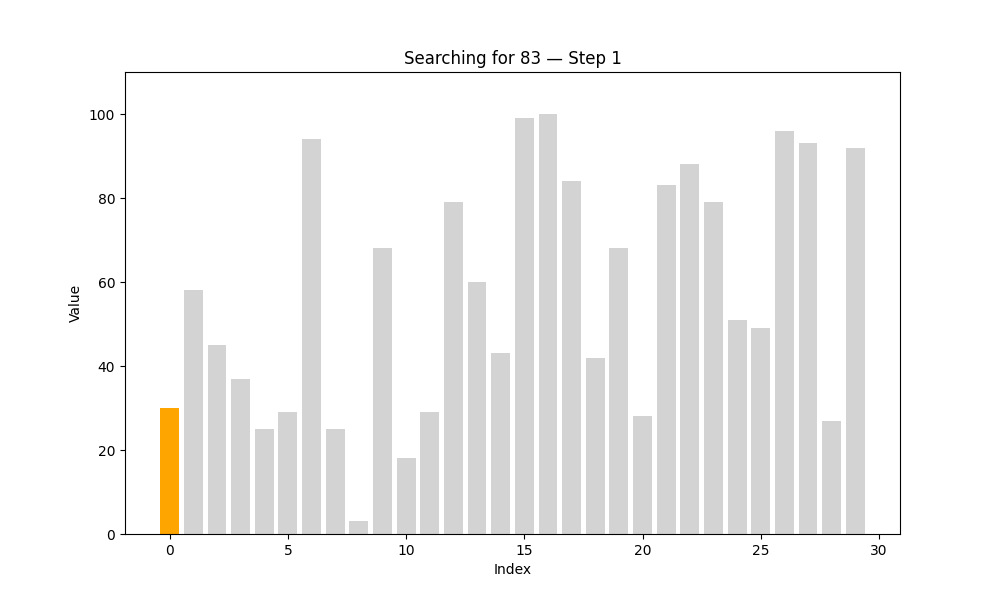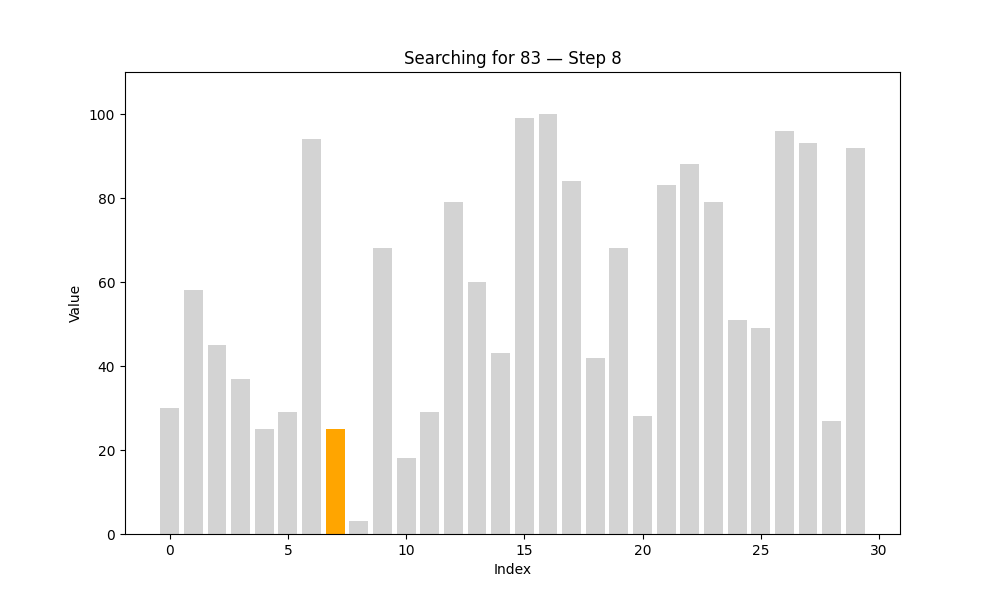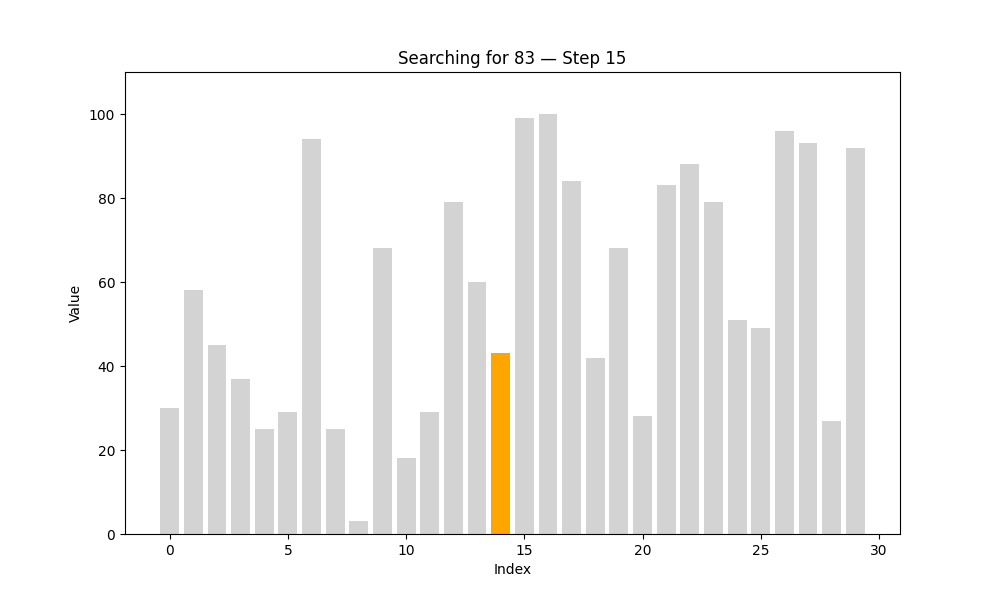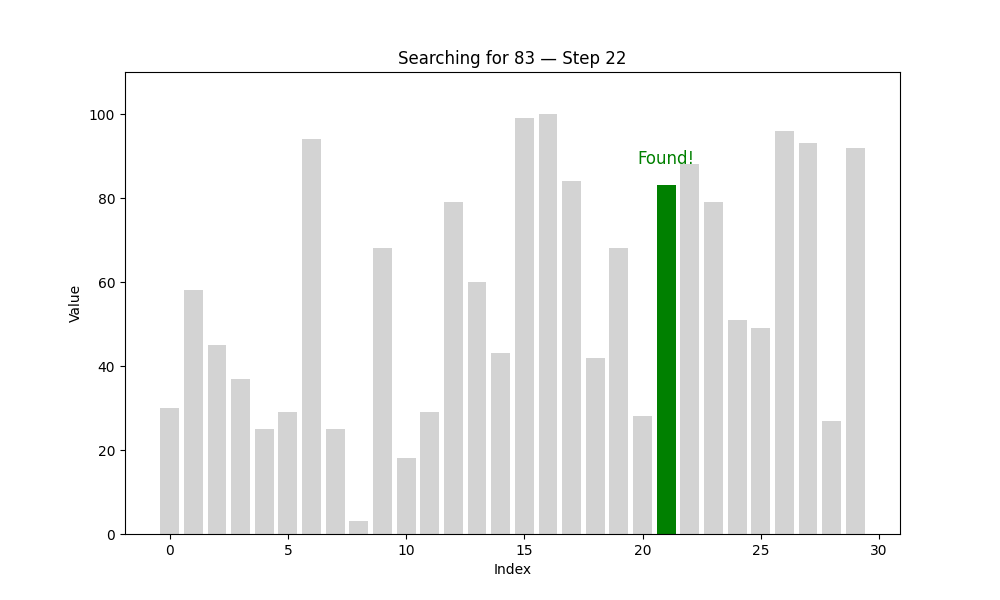
二分查找（Binary Search）

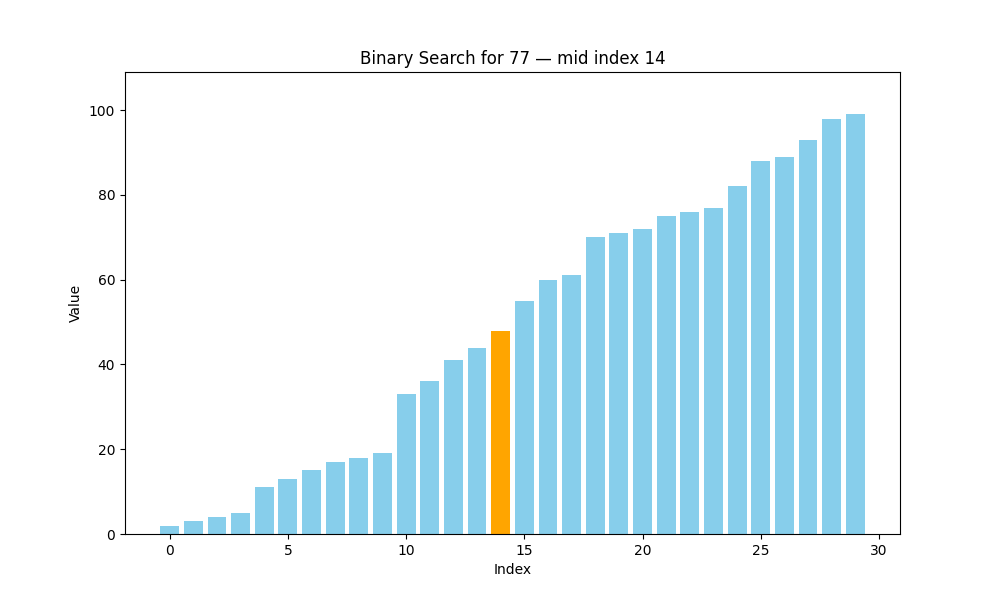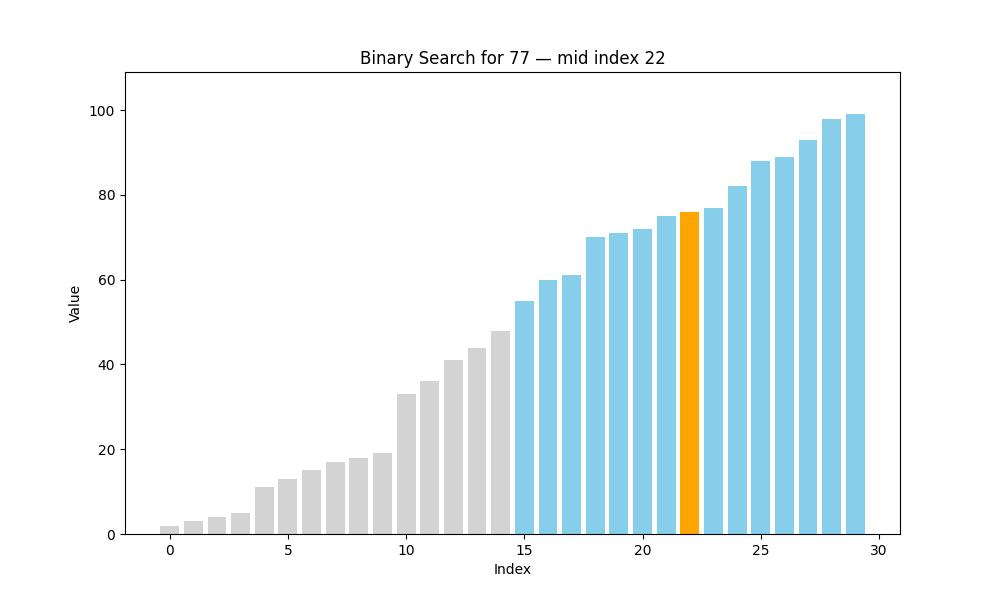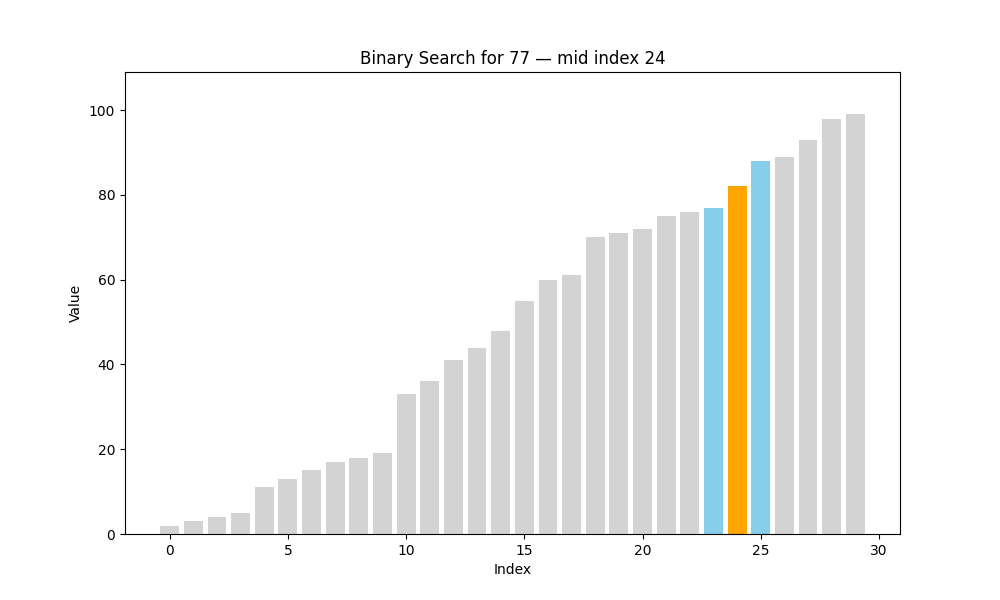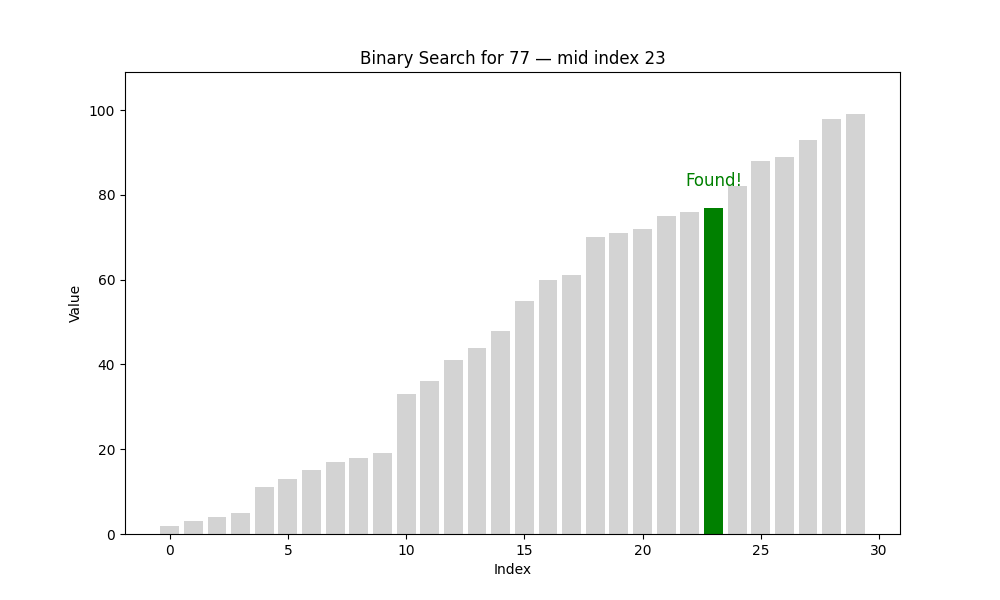
二分查找是一種高效的查找方法，但它有一個前提條件：待查找的列表必須是有序的。也就是說，在使用二分查找之前，我們要確保數據已經按照升序或降序排列好，否則該算法將無法正常工作。

---

? 二分查找的核心思想：分而治之（Divide and Conquer）

具體過程如下：

1. 將數組從中間分成兩部分；
2. 將目標值與中間元素進行比較：
   • 如果相等，則查找成功，返回該位置；
   • 如果目標值小于中間元素，說明目標在左半部分；
   • 如果目標值大于中間元素，說明目標在右半部分；
3. 僅在可能存在目標值的一半繼續查找；
4. 重復上述步驟，直到找到目標或范圍為空為止。

這種方法的效率極高：每次查找操作都將問題規模減半，時間復雜度為 $O({\log }_{2}n)$，遠優于線性查找的 $O(n)$，尤其在數據量較大時優勢更加明顯。

---

def binary_search(arr, target):steps = []low = 0high = len(arr) - 1while low <= high:mid = (low + high) // 2step = {'array': arr.copy(),'low': low,'high': high,'mid': mid,'found': arr[mid] == target}steps.append(step)if arr[mid] == target:breakelif arr[mid] < target:low = mid + 1else:high = mid - 1return steps

---

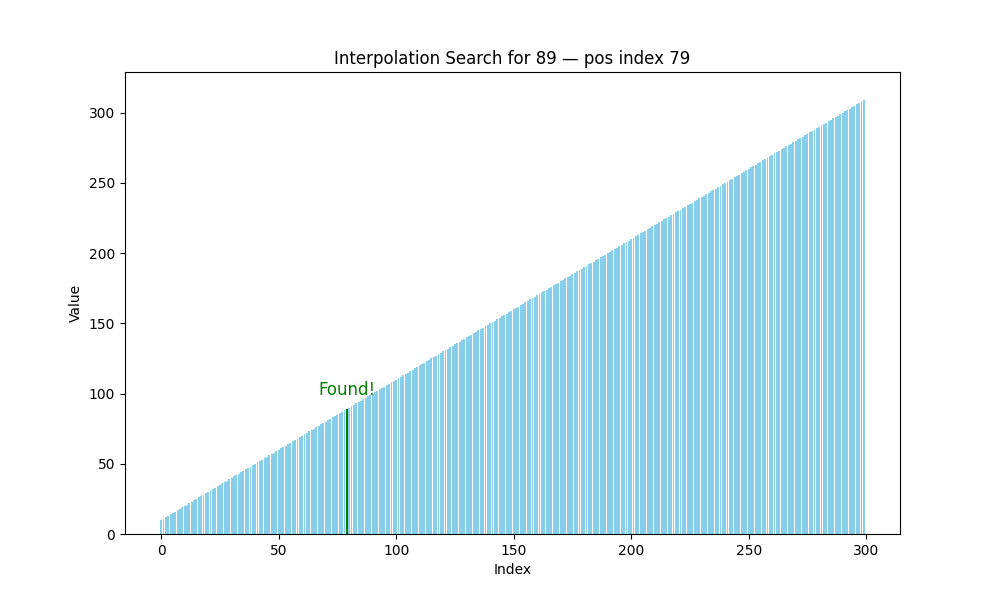
插值查找（Interpolation Search）

• 適用條件： 數據必須是有序且分布均勻
• 核心思想： 預測目標值可能出現的位置，而不是死板地取中間值

$$mid=low+\frac{(target?arr[low])?(high?low)}{arr[high]?arr[low]}$$

• 時間復雜度：
  • 最好：$O(\log \log n)$
  • 最壞：$O(n)$（分布極度不均）

---

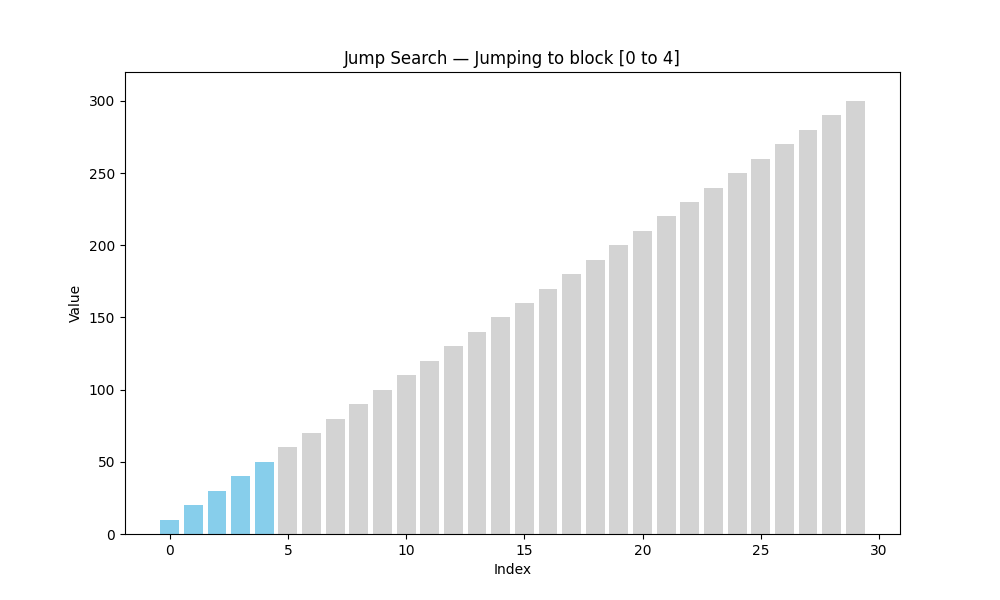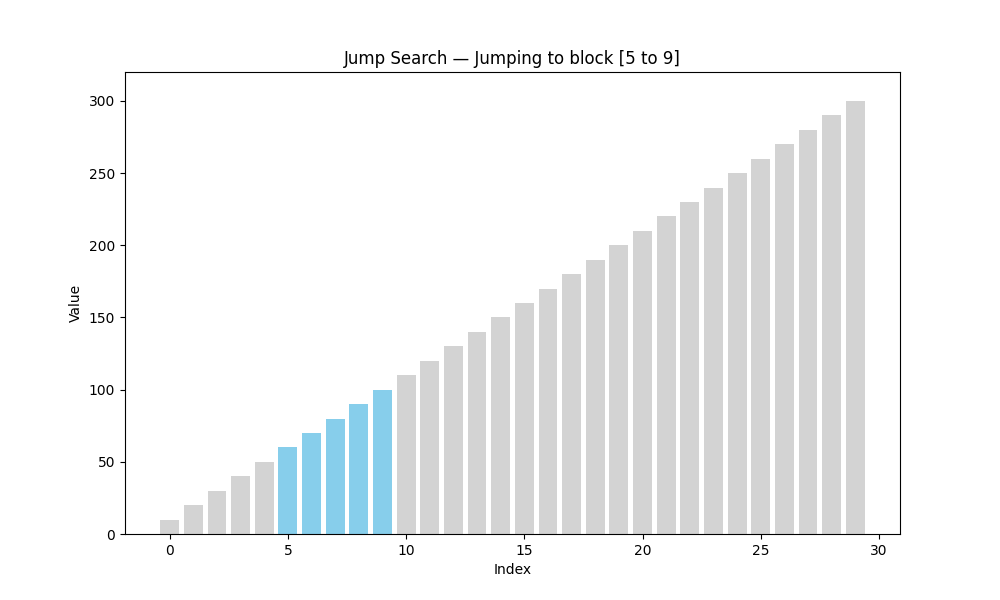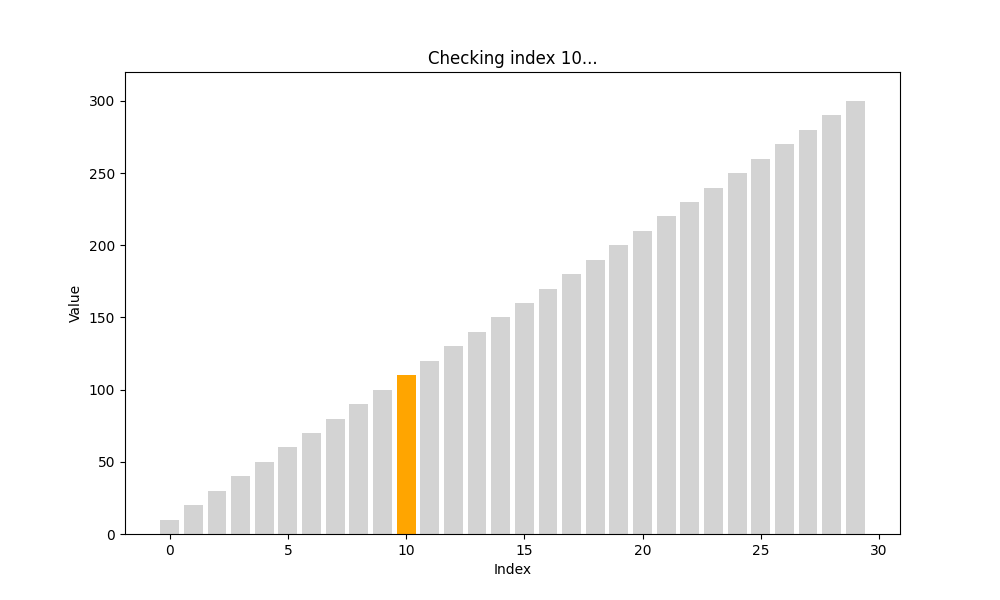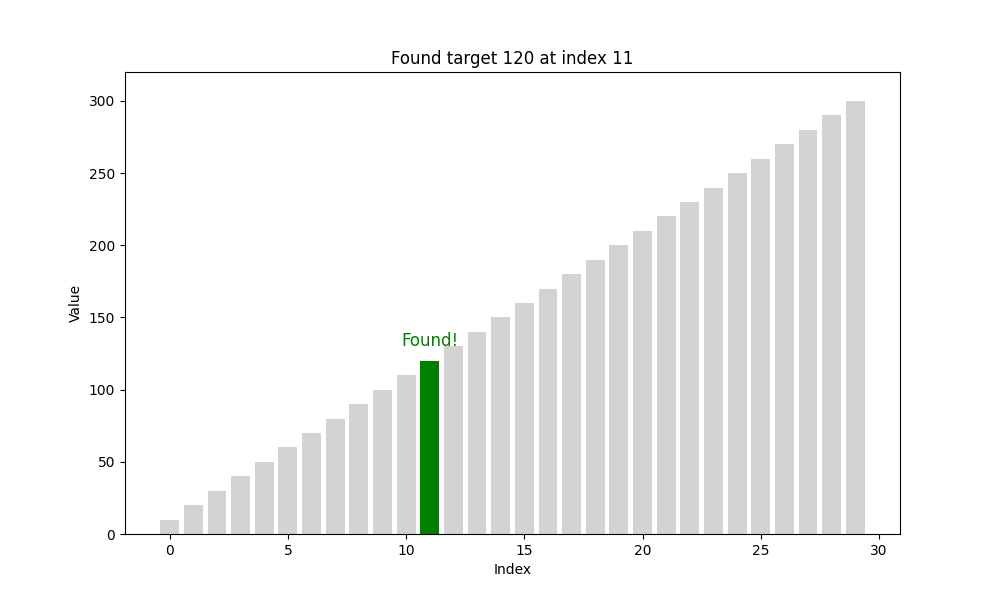
跳躍查找（Jump Search）

• 適用條件： 有序數組
• 核心思想： 以固定步長（如 $\sqrt{n}$）跳躍前進，找到目標所在區間后回退線性查找
• 時間復雜度： $O(\sqrt{n})$

---

哈希查找（Hash Search）

• 適用條件： 查找速度要求極高，數據量大，結構可以犧牲順序
• 核心思想： 使用哈希函數將關鍵字映射到數組中的某個索引位置
• 優勢： 插入和查找時間復雜度通常為 $O(1)$
• 挑戰： 哈希沖突（如鏈地址法、開放定址法）

---

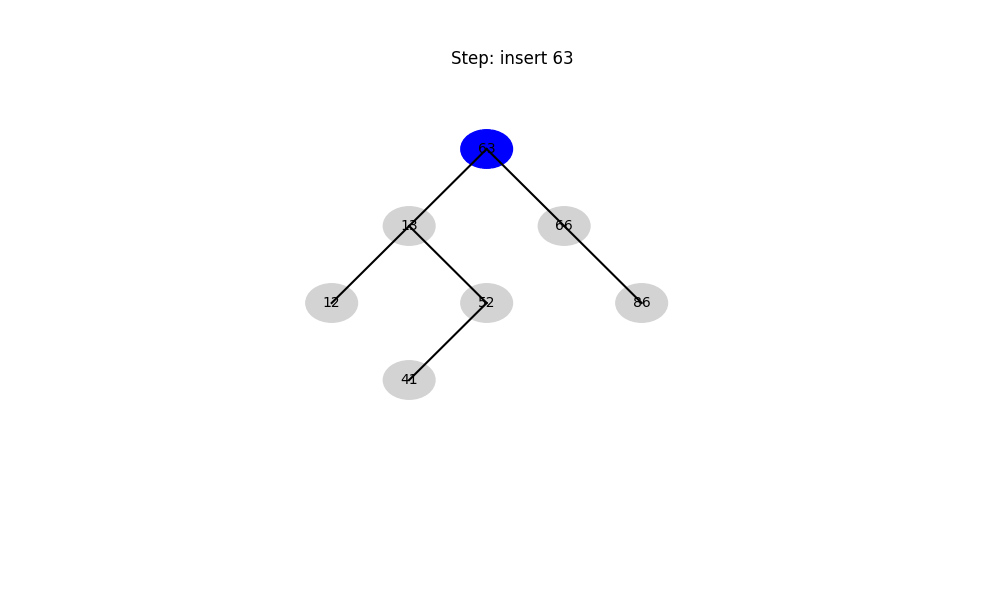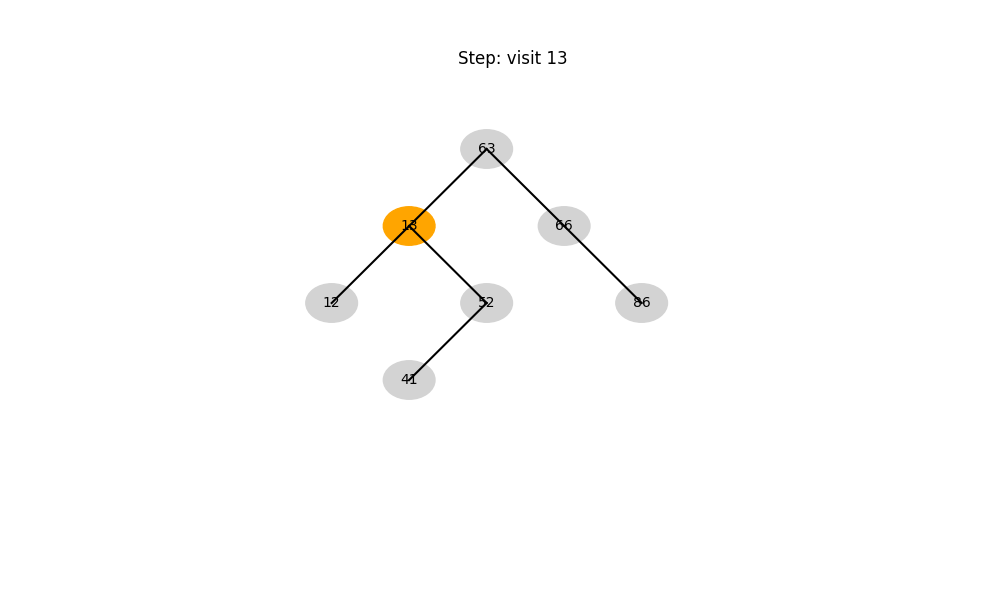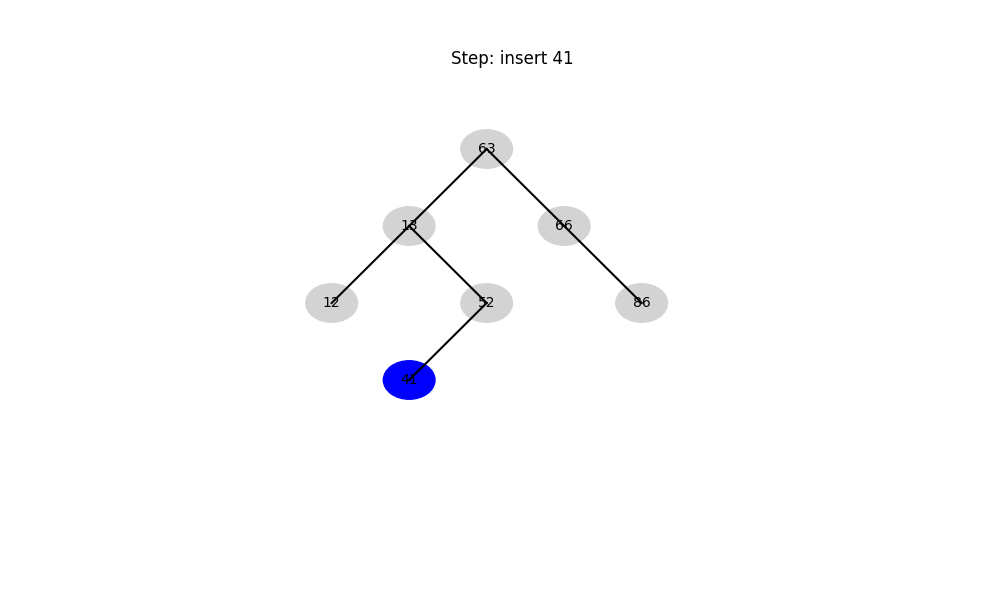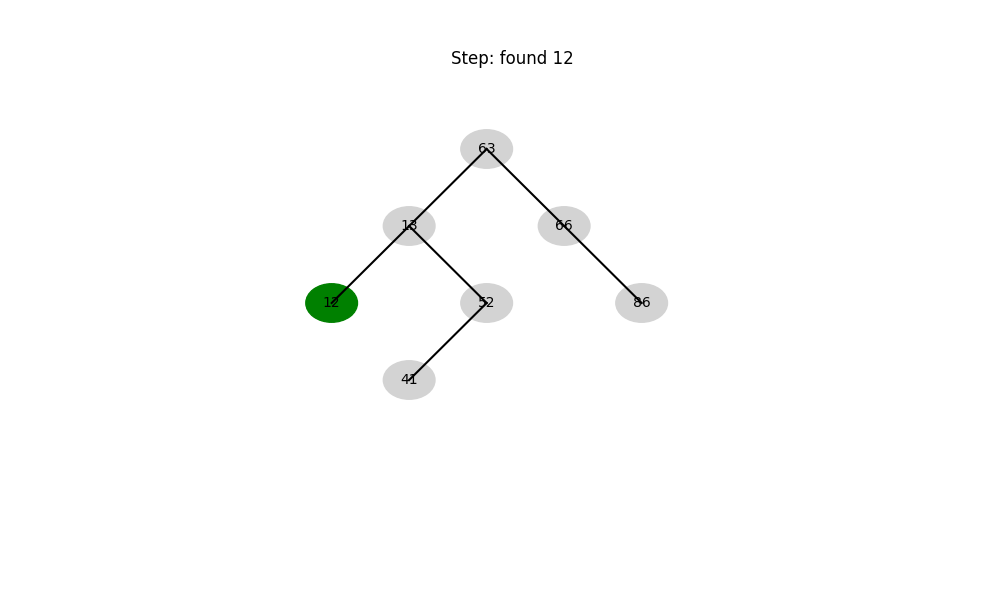
二叉搜索樹（Binary Search Tree, BST）

• 結構性質： 左子樹 < 根 < 右子樹
• 時間復雜度：
  • 平均：$O(\log n)$
  • 最壞：$O(n)$（退化成鏈表）

---

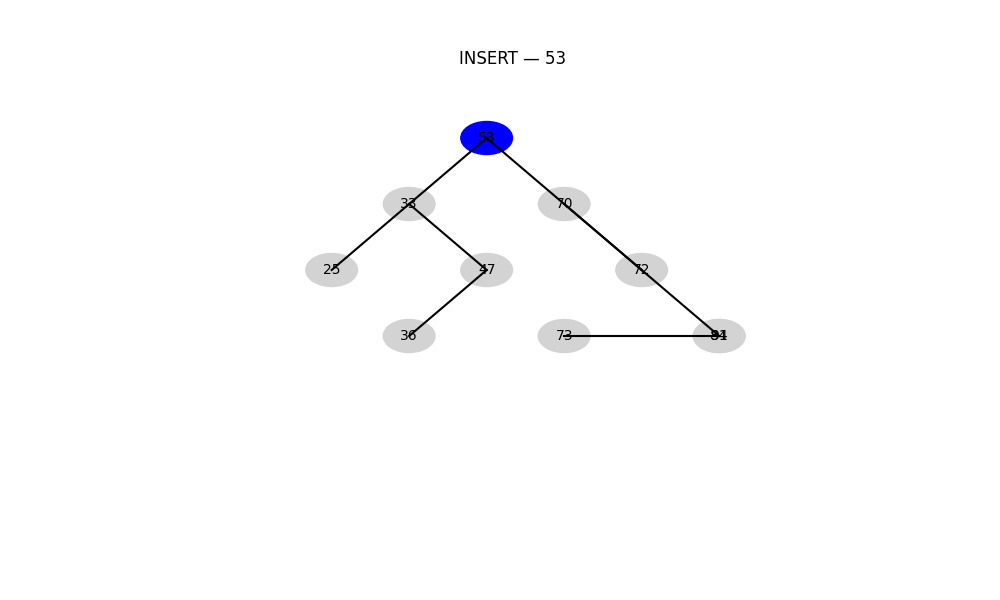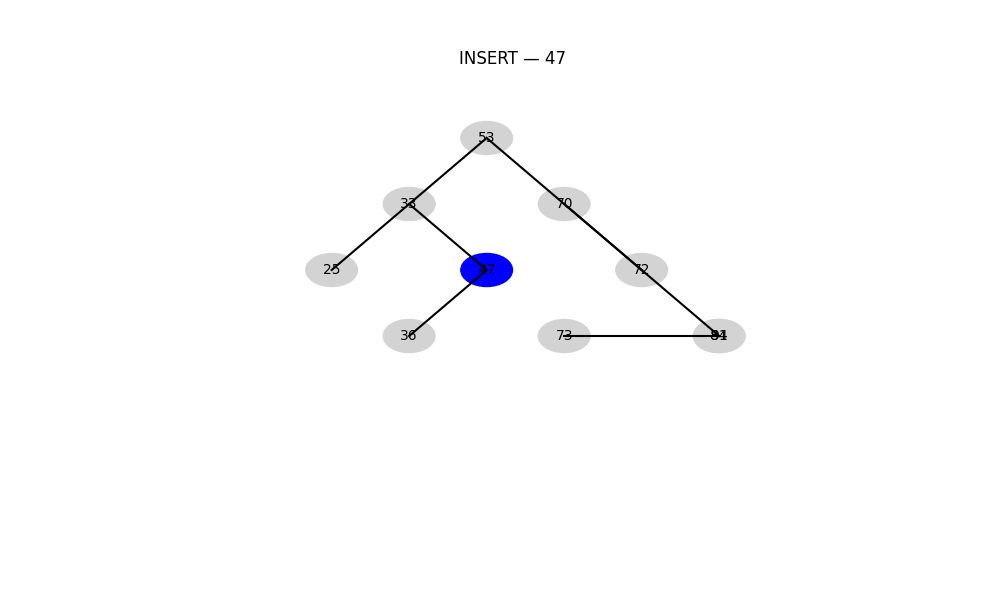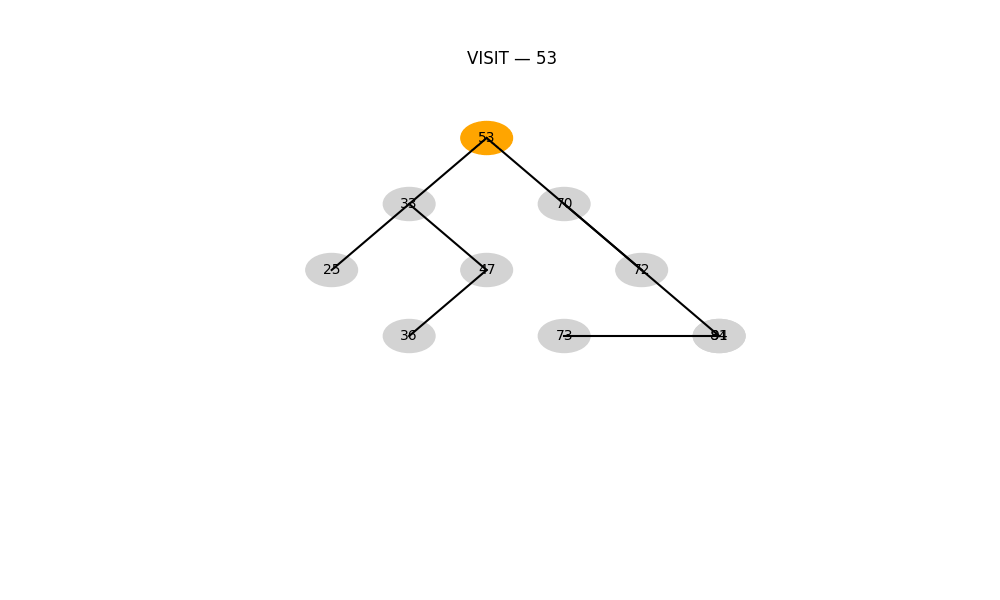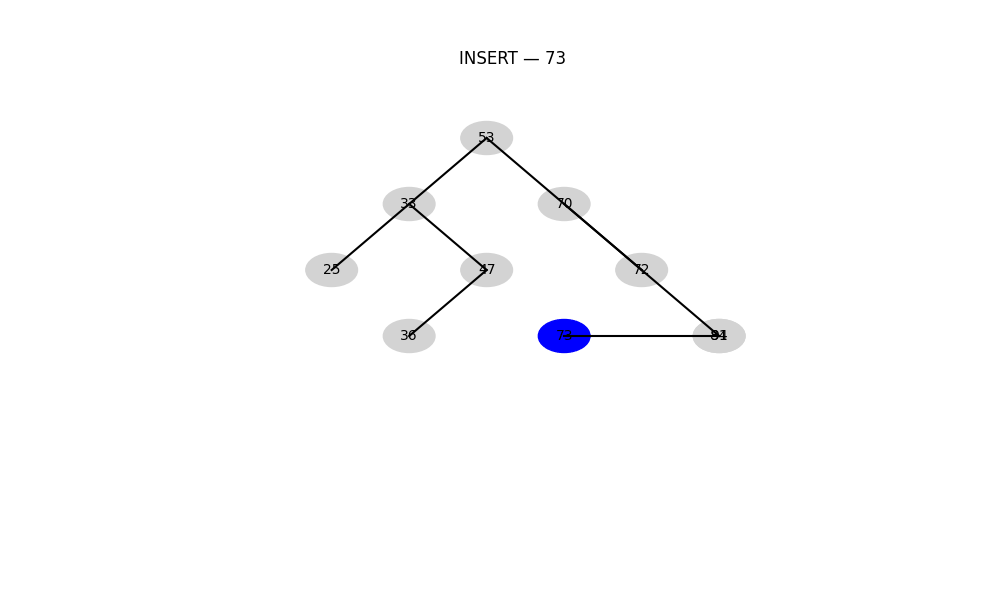
平衡二叉搜索樹（AVL 樹、紅黑樹等）

• 特性： 自動保持“樹的高度”平衡，防止性能退化
• 優勢： 所有操作最壞時間復雜度為 $O(\log n)$
• 適用： 高頻插入+查找操作，如操作系統調度、緩存結構

---

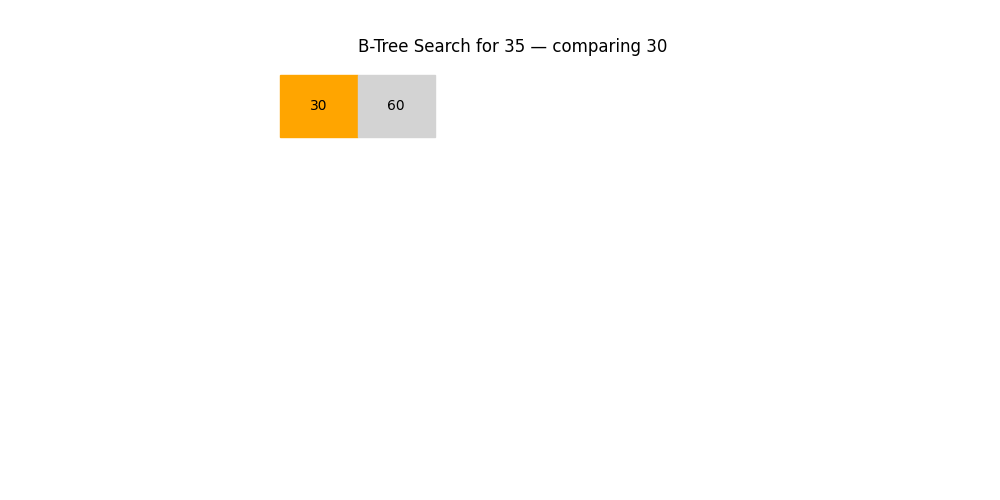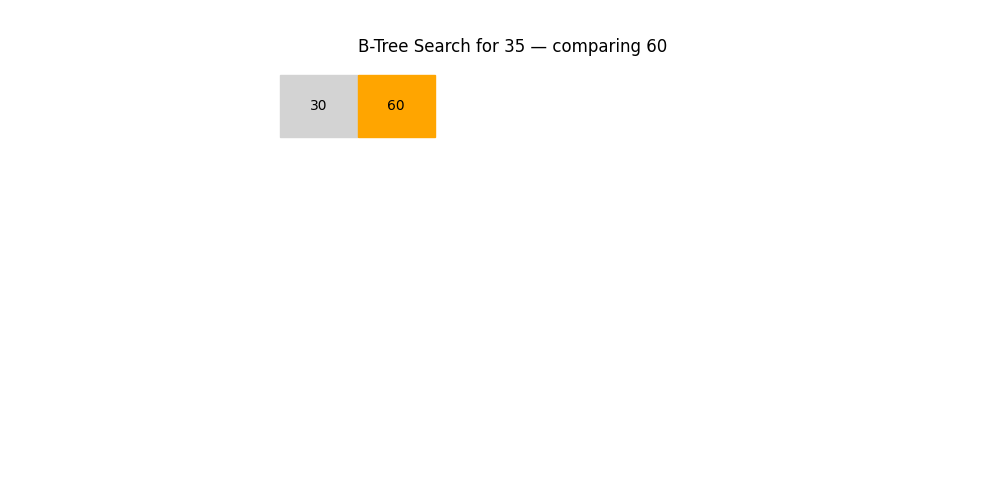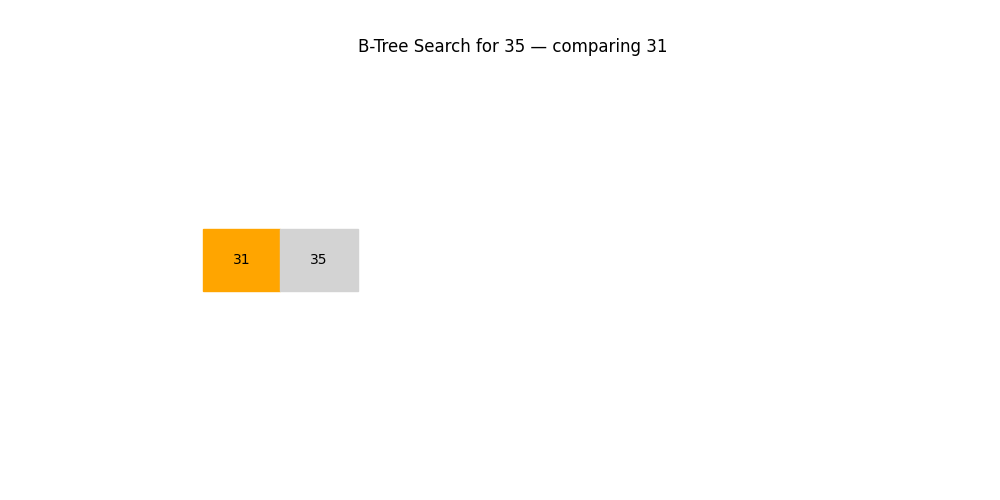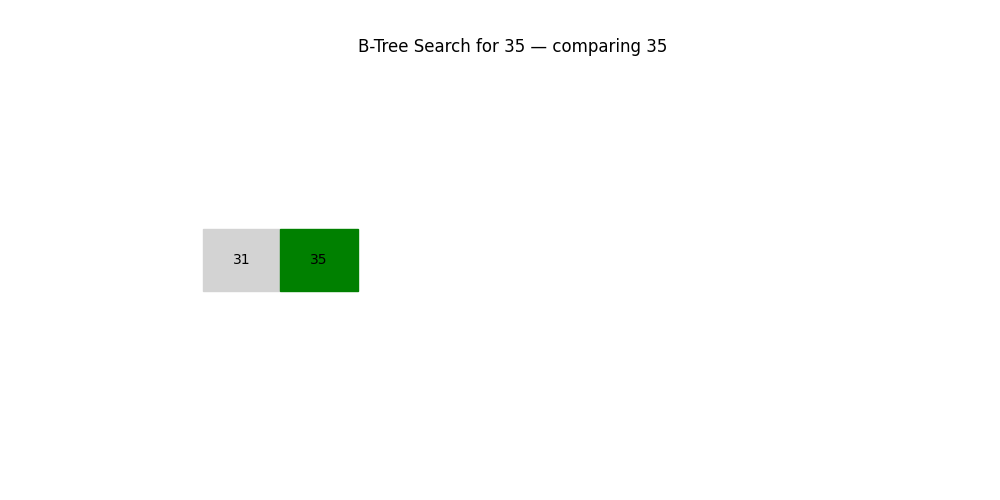
B 樹 / B+ 樹

• 用途： 用于數據庫、文件系統等對磁盤IO優化要求極高的場景
• 特點：
  • 多路搜索，不是二叉結構
  • 每個節點包含多個關鍵字
• 優勢： 能減少磁盤訪問次數，支持批量范圍查找

---

深度優先搜索（DFS）與廣度優先搜索（BFS）

• 應用場景： 圖結構查找、路徑規劃、社交網絡分析等
• 特點：
  • DFS：適合探索所有路徑（回溯）
  • BFS：適合找最短路徑或分層結構

---

指數查找（Exponential Search）

• 應用場景： 無法直接知道數據規模，如“無限數組”
• 過程：
  1. 快速擴大查找范圍（1, 2, 4, 8…）
  2. 找到目標值所在的范圍后使用二分查找
• 時間復雜度： $O(\log i)$，其中 $i$ 為目標位置

---