3.1 元素輸入法
元素輸入法是最簡單,也是最常用的一種矩陣的生成方法。例如:


注意:
- 整個矩陣必須用“[]”括起來;
- 元素之間必須用逗號“,”或空格分開;
- 矩陣的行與行之間必須用“;”或者回車鍵“Enter”隔開;
- 元素按照先列后行的方式進行存儲。
3.2 設定步長生成法
設定步長生成法用于生成一維行數組。
格式:x=a:inc:b
其中a是數組的第一個元素;inc是相鄰兩個元素之間的間隔;b是數組的最后一個元素。
例如:x=1:3:25

說明:
(1)若b-a是inc的整數倍,則最后一個元素是b;否則小于b。
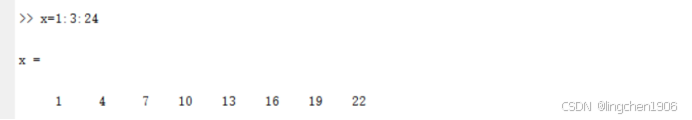
(2)若inc=1,可簡寫為x=a:b。

(3)inc可以取整數,也可以取復數。

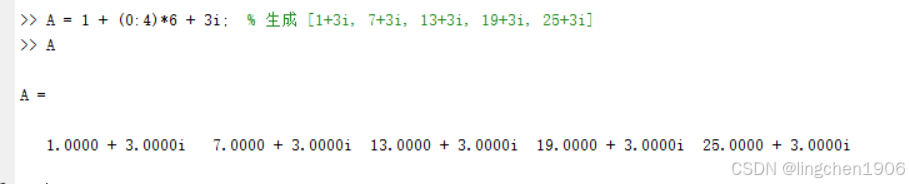
遇到的警告 "Colon operands must be real scalars" 是因為在 MATLAB 中使用冒號運算符?:?時,中間的步長值使用了復數?3i。
冒號運算符的正確語法是?start:step:end,其中?start、step?和?end?都必須是實數標量,而不能是復數。
在例子中,雖然寫了?1:3i+6:25,但 MATLAB 實際上忽略了復數部分的虛部,只使用了實部進行計算:
- 起始值:1
- 步長值:6(因為?
3i?的實部是 0,0+6=6) - 結束值:25
所以最終結果?A = [1 7 13 19 25]?實際上是按照?1:6:25?計算得到的,這就是為什么雖然有警告但仍然得到了結果。
如果你確實需要生成包含復數的數組,可以使用其他方法,例如:
3.3 均勻采樣生成法
均勻采樣生成法用于生成一維行數組。
格式:x=linspace(a,b,n)
其中,a,b分別為生成數組的第一個和最后一個元素;n為采樣總點數。
例如:x=linspace(1,25,3)
從定義可以看出,該指令的作用與x=a:(b-a)/(n-1):b相同。

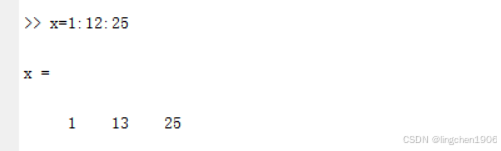
3.4 幾種特殊矩陣的創建
特殊矩陣的創建命令如下表:
命令 | 說明 |
[] | 空矩陣 |
zeros | 全零矩陣 |
ones | 全一矩陣 |
eye | 單位矩陣 |
magic | 魔方矩陣 |
rand | 均勻隨機矩陣 |
randn | 高斯隨機矩陣 |
diag | 對角矩陣 |
(1)空矩陣
A=[] ?%用于刪除某個元素或者矩陣。
例:把矩陣A的第一個元素刪除。
如下:
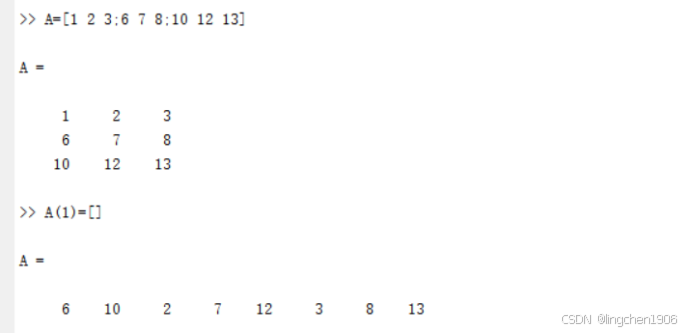
(2)全零矩陣
A=zeros(2,3) ?%生成元素全為零的2×3階矩陣。

(3)全一矩陣
A=ones(2,3) ??%生成元素全為1的2×3階矩陣。

(4)單位矩陣
A=eye(3,4) %使用eye(m,n)可得到一個允許的最大單位矩陣,其他位置補零。

(5)魔方矩陣
X=magic(3) ?%用于產生一個3×3階的魔方矩陣。
魔方矩陣(Magic Square)是一種特殊的n 階方陣,其核心特征是每行、每列以及兩條主對角線的元素之和都相等,這個相等的和被稱為 “魔數”(Magic Constant)。
魔方矩陣在數學、數論、組合數學以及趣味數學中都有重要地位,且具有深厚的歷史背景,古代文明(如中國、印度、阿拉伯等)都曾研究過這類矩陣。
魔方矩陣的核心性質
- 階數定義:通常以 “n 階” 表示,指矩陣的行數和列數均為 n(n≥1,且多為正整數)。
- 魔數計算:對于 n 階魔方矩陣(元素為 1 到 n2 的連續整數,即 “標準魔方矩陣”),其魔數固定為:
魔數 = n×(n2 + 1)÷2
例如:- 3 階魔方矩陣的魔數為 3×(9 + 1)÷2 = 15;
- 4 階魔方矩陣的魔數為 4×(16 + 1)÷2 = 34。
- 元素特點:標準魔方矩陣的元素是 1 到 n2 的連續整數,且每個數只出現一次(即 “幻方” 的經典定義);非標準魔方矩陣可以使用其他數字,但需滿足行、列、對角線和相等的條件。
常見階數的魔方矩陣示例
3 階魔方矩陣(最經典)
3 階魔方矩陣是最小的奇數階非平凡魔方矩陣,其元素為 1-9,每行、每列、對角線之和均為 15:
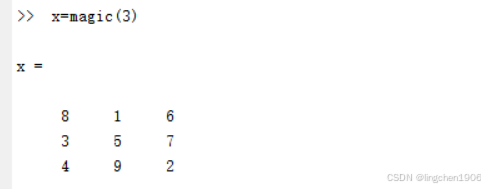
- 行:8+1+6=15,3+5+7=15,4+9+2=15;
- 列:8+3+4=15,1+5+9=15,6+7+2=15;
- 對角線:8+5+2=15,6+5+4=15。
4 階魔方矩陣(偶數階)
4 階魔方矩陣元素為 1-16,魔數為 34,例如:

魔方矩陣的分類
根據階數的奇偶性,魔方矩陣可分為兩類:
奇數階魔方矩陣(n 為奇數):
可通過 “Siamese 方法”(斜步法)構造,核心是從矩陣底部中間位置開始,按特定方向(通常是右上)依次填入數字,遇到邊界或已填元素時調整位置。
偶數階魔方矩陣:
當 n 為4 的倍數(如 4、8 階):可通過 “對稱交換法” 構造,將矩陣分為 4×4 子塊,交換特定位置的元素。
當 n 為2 的倍數但不是 4 的倍數(如 6、10 階):構造更復雜,需結合奇數階的構造方法分段處理(稱為 “單偶數階”)。
魔方矩陣的應用與意義
- 數學研究:作為組合數學的經典問題,其構造方法涉及數論和對稱性分析。
- 歷史文化:古代被視為神秘符號,如中國的 “洛書”(3 階魔方矩陣)被認為是最早的魔方矩陣之一,記載于《周易》等典籍中。
- 計算機科學:常用于算法設計(如矩陣填充、回溯法練習)和密碼學中的隨機數生成參考。
(6)隨機矩陣
1. rand()均勻隨機矩陣用于生成(0,1)區間上均勻分布的隨機變量,其基本語法如下:
rand([M,N,P,...] )
例:
A=rand(2,4) %生成隨機的2×4階矩陣

生成排列成M×N×P...多維向量的隨機數。如果只寫M,則生成M×M階矩陣;如果參數為[M,N],則可以省略到方括號。

2. randn()高斯隨機矩陣用于生成服從標準正態分布(均值為0,方差為1)的隨機數,其基本語法和rand()類似:
randn([M,N,P...])
生成排列成M×N×P...多維向量的隨機數。如果只寫M,則生成M×M階矩陣;如果參數為[M,N],可以省略掉方括號。


3. rand() 與 randn() 的核心對比
維度 | rand() | randn() |
分布類型 | (0, 1) 區間均勻分布 | 標準正態分布(均值 0,方差 1) |
語法共性 | 維度參數規則、括號省略邏輯完全一致 | 維度參數規則、括號省略邏輯完全一致 |
應用場景差異 | 需“無偏向隨機數”場景(如等概率模擬、均勻初始化) | 需“自然波動規律”場景(如噪聲模擬、正態分布物理量建模) |
4. 理解“生成排列成多維向量的隨機數”,需結合 Matlab 中數組的維度特性、函數參數規則來拆解,核心邏輯如下:
1. “多維向量”實為 多維數組
在 Matlab 語境中,此處“向量”是廣義的數組概念(突破數學中“一維向量”的狹義定義)。Matlab 支持創建任意維度的數組(如二維矩陣、三維“行-列-頁”結構、四維及以上張量),因此“多維向量”本質是多維數組。
2. M,N,P...的作用:定義各維度的長度
rand()/randn()?的參數 是維度尺寸參數,每個字母對應一個維度的“長度”:
- 第 1 個參數 ?→ 數組第 1 維的長度(如“行數”);
- 第 2 個參數 ?→ 數組第 2 維的長度(如“列數”);
- 第 3 個參數 ?→ 數組第 3 維的長度(如“頁數/層數”);
- 更多參數 → 對應更高維度的長度。
3. “排列成M×N×P... ”:按維度參數構造數組結構
函數會先根據M,N,P...的數量和數值,確定數組的維度數量和各維度大小,再在這個預定義結構中填充隨機數。結合場景具象化理解:
(1)二維數組(矩陣)場景
若輸入 2 個參數 M,N(如 rand(2, 4)):
- 維度數量:2 維(行、列);
- 各維長度:第 1 維(行)長度 = M=2,第 2 維(列)長度 = N=4;
- 結果:生成 2 行 4 列的二維數組(矩陣),每個元素是 rand()?生成的 (0,1) 均勻隨機數,或 randn()?生成的標準正態分布數。
(2)三維數組場景
若輸入 3 個參數M,N,P(如 rand(2, 3, 2)):
- 維度數量:3 維(行、列、頁);
- 各維長度:第 1 維(行)=M=1 ,第 2 維(列)=N=3?,第 3 維(頁)=P=2?;
- 結果:生成 “2 行 × 3 列 × 2 頁”?的三維數組。可想象為“2 個獨立的 2 行 3 列矩陣疊在一起”,每個位置填充隨機數。



(3)更高維數組場景
若輸入 4 個參數M,N,P,Q(如 rand(1, 2, 3, 4)):
- 維度數量:4 維;
- 各維長度:第 1 維 = M=1,第 2 維 =N=2?,第 3 維 = P=3,第 4 維 = Q=4;
- 結果:生成 1×2×3×4?的四維數組,結構由 4 個維度長度共同定義,每個元素位置填充隨機數。




5. 在 Matlab 中,“擴展數組到更高維度”可通過生成新的高維數組或改造已有數組維度實現。結合rand()/randn()?的語法邏輯,以下是詳細方法拆解:
對已有數組擴展維度(非隨機數組的維度改造)
若要對已存在的非隨機數組(如數值矩陣、向量)擴展維度,可通過以下通用方法:
1. 使用 cat() 函數“沿維度拼接”
cat(DIM, A, B, ...)?可沿指定維度 DIM?拼接多個數組,實現維度擴展。
示例:將兩個 2×3 矩陣沿第 3 維拼接,得到 2×3×2 三維數組:
A = ones(2, 3); ?% 2×3 全1矩陣
B = zeros(2, 3); % 2×3 全0矩陣
C = cat(3, A, B);% 沿第3維拼接,生成 2×3×2 三維數組

2. 使用 reshape() 函數“重塑維度”
reshape(A, M, N, P, ...)?可將數組 A?重塑為指定維度的新數組(要求元素總數匹配)。
示例:將 1×6 行向量重塑為 2×3 矩陣(二維),或 1×2×3 三維數組:
V = 1:6; ?????????????????% 1×6 行向量(元素總數6)
M2 = reshape(V, 2, 3); ???% 重塑為 2×3 矩陣(2×3=6,元素總數匹配)
M3 = reshape(V, 1, 2, 3); % 重塑為 1×2×3 三維數組(1×2×3=6,元素總數匹配)

3. 直接賦值“擴展維度”
對數組的新維度位置直接賦值,Matlab 會自動擴展維度并填充默認值(如 NaN?或 0,依場景而定)。
示例:將 2×3 矩陣擴展為 2×3×2 三維數組:
A = ones(2, 3); ?% 2×3 矩陣
A(:, :, 2) = 2; ?% 給第3維的第2層賦值,自動擴展維度為 2×3×2

4. 擴展數組維度的核心路徑
場景 | 核心方法 | 示例(代碼片段) |
生成隨機高維數組 | 用 rand()/randn()?的多維度參數 [M, N, P, …]?定義維度大小 | rand(2, 3, 2)?生成 2×3×2 均勻隨機三維數組 |
擴展已有數組維度 | ① cat()?沿指定維度拼接;② reshape()?重塑維度;③ 直接賦值新維度位置 | cat(3, A, B)?沿第3維拼接數組;reshape(V, 1, 2, 3)?重塑維度 |
通過上述方法,可以靈活地在 Matlab 中創建或改造數組維度,覆蓋從二維矩陣到高維張量的多樣化需求。
(7)對角矩陣
(1)diag(x),當輸入x為向量的時候,輸出結果為對角矩陣。
當輸入x是一個向量(可以是行向量或列向量)時,diag(x)的輸出是一個對角矩陣:
- 矩陣的主對角線(從左上角到右下角的對角線)元素為向量x的各個分量;
- 矩陣的其他位置元素均為0;
- 矩陣的階數(行數和列數)等于向量x的長度。
示例:
若x = [a, b, c](長度為3的行向量),則:
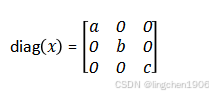
具體數值例子:設x = [1, 2, 3],則:
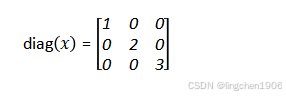
(2)diag(x,k),形成以x作為第k條對角線元素,其他位置為0的矩陣。
當輸入x是向量,且額外指定參數k時,diag(x, k)的輸出是一個非主對角線矩陣:
- 矩陣的第k條對角線元素為向量x的各個分量;
- 其他位置元素均為0;
- k的含義:k=0表示主對角線,k>0表示主對角線上方第k條對角線,k<0表示主對角線下方第|k|條對角線;
- 矩陣的階數:若x長度為n,則矩陣階數為n + |k|(確保x的所有元素能放在第k條對角線上)。
示例:
設x = [1, 2](長度為2),k=1(主對角線上方第1條對角線),則矩陣階數為2 + 1 = 3,輸出為:
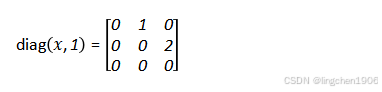
- 若k=-1(主對角線下方第1條對角線),輸出為:
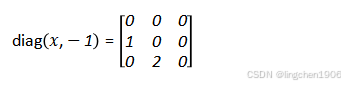
(3)當輸入x為矩陣的時候,輸出結果為提取該矩陣對角線元素形成的列向量。
當輸入x是一個矩陣時,diag(x)的輸出是一個列向量:
向量的元素為矩陣x的主對角線元素(從左上角到右下角依次提取);
向量長度等于矩陣x的階數(若x是n×n矩陣,則向量長度為n)。
示例:
設x是3×3矩陣:

其主對角線元素為1, 5, 9,則:
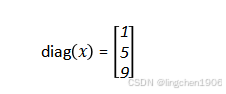
(JProfiler、arthas、jdk調優工具(命令行)))




)


)





)


)

