多智能體系統（Agent-Based Model, ABM）和強化學習（Reinforcement Learning, RL）是兩個不同但可結合的概念，尤其在復雜系統建模和人工智能領域有重要應用。下面分別解釋它們，并說明二者的關聯：

1. 多智能體系統（Agent-Based Model, ABM）

定義

ABM 是一種自底向上（簡單規則能產生復雜秩序）的計算機模擬方法，通過定義大量自主交互的智能體（Agents（黃色字體） 及其行為規則，模擬復雜系統的宏觀現象（如市場波動、流行病傳播、生態系統演化等）。

a:“自底向上”（Bottom-Up）是一種方法論或設計思想，指從系統最基礎的組成部分（底層）出發，通過定義其簡單行為和交互規則，最終涌現（Emergence） 出復雜的整體現象。它與“自頂向下”（Top-Down）相對，后者是從宏觀整體目標出發，逐層分解為子任務的設計方式

用ABM的例子理解“自底向上”

在多智能體系統（ABM） 中，“自底向上”體現為：

1. 起點是微觀個體：
   先定義系統中每個智能體（Agent） 的屬性和行為規則（例如：

   • 個體屬性：位置、能量值、年齡

   • 行為規則：移動、覓食、躲避天敵、繁殖）。

2. 關注局部交互：
   智能體僅根據自身狀態和鄰近環境做決策（例如：

   • “如果周圍有食物，則靠近；如果發現捕食者，則逃跑”）。

3. 宏觀現象自然涌現：
   所有智能體并行行動并持續交互后，系統會自發產生復雜的全局模式（例如：

   • 鳥群在沒有指揮的情況下形成編隊飛行；

   • 螞蟻通過簡單信息素規則構建出復雜的巢穴結構）。

? 核心思想：復雜系統無需中央控制，微觀個體行為的疊加即可生成宏觀秩序。

對比“自頂向下”（Top-Down）

維度	自底向上（Bottom-Up）	自頂向下（Top-Down）
起點	基礎組件（如智能體、細胞）	整體目標（如系統功能、架構）
設計邏輯	組件行為 → 系統現象（涌現）	整體目標 → 分解為子任務 → 實現
控制方式	分布式、無中心控制	集中式、中央調控
典型應用	ABM、生物演化、群體智能	傳統工程（如建樓、編寫軟件）

現實中的“自底向上”案例

1. 螞蟻覓食：
   每只螞蟻只遵循“釋放信息素+跟隨高濃度路徑”的簡單規則，最終整個蟻群找到食物源的最短路徑。

2. 金融市場波動：
   每個交易者（智能體）根據個人策略買賣股票，無數交易行為的疊加導致股價漲跌（而非由中央機構直接設定價格）。

3. 免疫系統：
   免疫細胞獨立識別并攻擊病原體，整體形成免疫防御網絡，無需“大腦”指揮。

為什么ABM必須用“自底向上”？

許多復雜系統（如社會、生態系統）的本質是去中心化的：

• 無法通過預設全局方程描述（例如無法用一個公式預測疫情傳播的所有細節）；

• 微觀個體的異質性和隨機交互會導致“蝴蝶效應”。
  ABM通過模擬底層個體行為，更真實地還原這類系統的動態演化。

總結：“自底向上” = 從局部個體出發 → 通過交互 → 生成全局復雜模式
它揭示了一個深刻原理：簡單規則能產生復雜秩序（Simple rules create complex behaviors）。

智能體 = 虛擬世界中的獨立個體（比如：游戲里的NPC、螞蟻群中的單只螞蟻、股市里的一個散戶投資者），它能自己觀察環境、做決策、和其他個體互動，最終影響整個系統。

1. 自主性（Autonomy）→ “有腦子，自己拿主意”

• 做什么：智能體不需要外部指揮，能根據自身目標獨立做決策。

2. 交互性（Interaction）→ “會社交，能合作/競爭”

• 做什么：智能體之間能溝通、合作、競爭甚至欺騙。

3. 適應性（Adaptation）→ “吃一塹長一智”

• 做什么：智能體能根據經驗調整行為（尤其在強化學習中）。

核心邏輯循環長這樣：

while True:  # 持續自主運行1. 觀察環境（收集周圍信息）2. 分析自身狀態（健康？疲勞？）3. 根據規則/學習策略做決策（移動？休息？）4. 執行動作（向前走一步）5. 與其他智能體互動（交換物資、傳遞消息）

特點	意味著什么	反例
自主	自己決定干什么	被遙控的玩具車
交互	會合作、競爭、溝通	孤島上的魯濱遜
有目標	努力達成任務（生存/賺錢等）	隨波逐流的樹葉
能適應	從經驗中學習（高級智能體）	一成不變的時鐘

---

核心特點

• 個體視角：每個智能體具有獨立屬性（位置、狀態、策略等）和行為規則（移動、決策、交互）。

• 去中心化：宏觀現象涌現自智能體間的局部交互，無需全局控制。

• 動態演化：系統隨時間推進，智能體根據環境和其他智能體的行為調整策略。

• 應用場景：社會學、經濟學、生物學、城市規劃等復雜系統研究。

示例

• 模擬股市中投資者（智能體）的買賣行為如何引發市場波動。

• 預測疫情中個體接觸如何影響傳播速度。

  ---

  2. 強化學習（Reinforcement Learning, RL）

  定義

  RL 是一種機器學習范式，智能體通過試錯學習= 像生物進化一樣實踐出真知，在環境中采取行動以最大化累積獎勵。核心是馬爾可夫決策過程（MDP）。

試錯學習在強化學習（RL）中如何運作？

假設訓練一個機械狗學會走路的RL模型：

步驟	試錯學習過程	對應RL術語
1.?嘗試動作	機械狗隨機向前邁腿	行動（Action）
2.?觀察結果	摔倒/平穩站立/向前移動	狀態（State）
3.?獲得反饋	摔倒：扣分（懲罰）	獎勵（Reward）
	移動：加分（獎勵）
4.?更新策略	減少導致摔倒的動作概率	策略優化（Policy Update）
	增加能移動的動作概率
5.?重復循環	持續嘗試新動作 → 積累經驗 → 越走越好	學習收斂

馬爾可夫決策過程（MDP）：馬爾可夫決策過程（Markov Decision Process, MDP） 是強化學習（Reinforcement Learning）的核心數學框架，用于建模智能體（Agent）在環境中做序貫決策的問題。它的核心思想是：未來的狀態只取決于當前狀態和動作，與過去無關。

一、MDP的5大要素（用游戲《超級馬里奧》類比）

MDP要素	定義	游戲中的例子
狀態（State）	環境的當前情況	當前畫面信息：馬里奧位置、敵人位置、金幣數等
動作（Action）	智能體能做的行為	按手柄鍵：← → ↑ ↓（左移/右移/跳躍/蹲下）
獎勵（Reward）	動作的即時反饋（數值）	吃金幣+1分，踩死敵人+2分，掉進坑里-10分（游戲結束）
狀態轉移（Transition）	動作如何改變環境狀態	按→鍵后，馬里奧向右移動一格（可能觸發敵人靠近）
折扣因子（γ）	衡量未來獎勵的重要性（0≤γ<1）	γ=0.9：未來1步的獎勵折算為90%，未來10步只剩35%

二、現實中的MDP應用

場景	狀態（State）	動作（Action）	獎勵（Reward）
自動駕駛	車輛位置、周邊障礙物	轉向/加速/剎車	安全抵達+100，碰撞-100，平穩行駛+0.1/秒
推薦系統	用戶歷史點擊+當前頁面	推送商品A/B/C	點擊+1，購買+10，忽略-0.1
機器人抓取	機械臂角度+目標物體位置	關節轉動方向/力度	抓取成功+50，掉落-20，耗時-0.01/秒

MDP = 環境的狀態轉移 + 智能體的決策目標

三、與非馬爾可夫過程的區別

若狀態不能完全描述環境歷史信息，則MDP失效 → 需升級為：

• 部分可觀測MDP（POMDP）：如打牌時看不到對手手牌。

• 循環神經網絡（RNN）：用記憶單元存儲歷史信息（如語言翻譯）。

---

• 核心要素

• 智能體（Agent）：學習者與決策者。

• 環境（Environment）：智能體交互的外部系統。

• 狀態（State）：環境的當前情況。

• 動作（Action）：智能體的行為選擇。

• 獎勵（Reward）：環境對動作的即時反饋。

• 目標：學習最優策略（Policy）以最大化長期獎勵。

• 學習機制

  智能體通過探索（嘗試新動作）和利用（選擇已知高獎勵動作）來優化策略，常用算法包括：

• Q-Learning、DQN（深度Q網絡）

• 策略梯度（Policy Gradient）

• Actor-Critic 方法

• 應用場景

  游戲AI（AlphaGo）、機器人控制、自動駕駛等。

  ---

3. ABM 與 RL 的結合：多智能體強化學習（MARL）

當ABM中的智能體具備學習能力時，可引入強化學習，形成多智能體強化學習（Multi-Agent RL, MARL）。這是當前AI研究的熱點。

關鍵挑戰

• 環境非平穩性：多個智能體同時學習導致環境動態變化。

• 信用分配：如何將系統級獎勵公平分配給個體？

• 合作與競爭：智能體目標可能沖突（競爭）或一致（合作）。

解決方法

• 集中式訓練+分布式執行：訓練時共享信息，執行時獨立行動（如MADDPG）。

• 通信機制：智能體學習溝通協議以協作（如CommNet）。

• 博弈論框架：用納什均衡等概念建模智能體交互（如Fictitious Play）。

應用場景

• 自動駕駛車隊協同優化路線。

• 多機器人協作搬運物體。

• 電力市場中多個發電商的動態競價策略。

  ---

  4. 對比總結

維度	多智能體系統（ABM）	強化學習（RL）	結合（MARL）
核心目標	模擬復雜系統涌現現象	學習最大化累積獎勵的策略	智能體在交互中學習協作/競爭策略
智能體行為	預定義規則或簡單啟發式	通過試錯優化策略	自適應學習策略
系統動態	由局部交互驅動	由獎勵函數驅動	學習與交互共同驅動
典型應用	社會模擬、流行病傳播	游戲AI、機器人控制	多機器人系統、智能交通

5. 通俗理解

• ABM 像模擬一群鳥的飛行：每只鳥按簡單規則（避免碰撞、跟隨鄰居）行動，整體形成鳥群。

• RL 像訓練一只狗：做對動作給獎勵，最終學會指令。

• MARL 則是訓練一群協作的狗：每只狗需學習如何與其他狗配合完成任務（如共同拉雪橇）。

二者結合為研究智能群體行為提供了強大工具，尤其在去中心化決策、分布式AI系統中前景廣闊。

---

本項目基于2015年全國大學生數學建模競賽B題，使用多智能體系統(Agent-Based Model)和強化學習方法來研究出租車資源配置問題。通過創新的建模方法，實現了對城市出租車供求關系的動態分析和優化。

通過對題目的理解與分析，可以知道問題背景:

? ? ? 隨著“互聯網+”時代的到來，多家公司依托移動互聯網建立了打車軟件服務平臺，實現了乘客與出租車司機之間的信息互通。為了緩解“打車難”問題，各平臺推出了多種出租車補貼方案。然而，這些方案可能存在不足，需要設計新的補貼方案以改善現狀。

可以提取到的要點有：

1.供求匹配程度分析：需要量化不同時空下出租車供給與乘客需求之間的匹配情況。

2.補貼方案影響評估：評估現有補貼方案對緩解打車難問題的效果。

3.新補貼方案設計：設計新的補貼方案，并通過模型驗證其合理性。（多智能體系統（MAS）和強化學習方法可以構成第三問中設計新打車軟件服務平臺補貼方案的一種可行模型框架。）

分析方法

• 數據收集：收集出租車軌跡數據、乘客打車請求數據、補貼方案數據等。
• 供求匹配指標：定義如“打車成功率”、“平均等待時間”等指標來量化供求匹配程度。
• 補貼方案建模：將補貼方案建模為影響出租車司機和乘客行為的因素，分析其對供求關系的影響。
• 強化學習優化：使用強化學習來優化補貼策略，以最大化某種長期獎勵（如乘客滿意度、出租車利用率）。

怎么去理解第一題：

問題本質、現有方案邏輯、核心矛盾、數據支撐四個維度展開：

一、理解題目：明確問題本質與目標

1. 題目定位
   第一題通常要求分析現有補貼方案的設計邏輯、實施效果及存在的問題，為后續設計新方案提供對比基準。

   2.核心目標

   二、解決步驟：系統性分析現有方案

   • 示例題目：
     “分析當前主流打車軟件（如滴滴、Uber）的乘客與司機補貼策略，指出其設計缺陷及對出租車資源配置效率的影響。”

     • 識別現有方案的目標用戶、激勵手段、成本結構。

     • 量化分析補貼對供需匹配、市場效率、用戶行為的影響。

     • 提煉關鍵矛盾（如“補貼導致司機挑單”“高峰時段供需失衡加劇”）。

       ---

   步驟1：拆解現有補貼方案類型

   按補貼對象和場景分類，典型方案包括：

   • 乘客端補貼：
     • 起步價折扣（如首單立減5元）
     • 動態折扣（根據供需比調整，如非高峰時段8折）
     • 忠誠度獎勵（如連續打車3次返現10元）
   • 司機端補貼：
     • 高峰時段溢價（如早晚高峰每單額外補貼2元）
     • 長距離訂單補貼（如訂單超過10公里后每公里補貼0.5元）
     • 空駛補償（如司機在特定區域等待超過10分鐘未接單，補償5元）
   • 綜合補貼：
     • 平臺促銷活動（如“周末打車全城5折”）
     • 節假日專項補貼（如春節期間司機接單獎勵翻倍）

   步驟2：分析補貼方案的設計邏輯與目標**

   • 乘客端邏輯：
     • 目標：降低打車門檻，吸引新用戶，提高非高峰時段需求。
     • 手段：通過價格敏感度測試（如A/B測試）確定最優折扣力度。
   • 司機端邏輯：
     • 目標：激勵司機在供需緊張時段/區域出車，減少空駛。
     • 手段：基于歷史數據預測高峰時段，動態調整補貼系數。
   • 平臺端邏輯：
     • 目標：平衡供需以提升匹配率，同時控制補貼成本占比（如不超過訂單金額的15%）。

   ---

   步驟3：量化評估補貼方案的實施效果**

   通過數據指標驗證方案有效性：

   • 乘客端效果：
     • 補貼后訂單量變化（如起步價折扣使訂單量提升20%）
     • 用戶留存率（如忠誠度獎勵使月活用戶增加15%）
   • 司機端效果：
     • 高峰時段接單率（如溢價補貼使接單率從60%提升至85%）
     • 空駛率變化（如空駛補償使空駛時間減少30%）
   • 市場效率效果：
     • 供需匹配率（如動態折扣使匹配率從70%提升至85%）
     • 乘客平均等待時間（如補貼優化后等待時間縮短至5分鐘內）

   ---

   步驟4：識別現有方案的核心矛盾與缺陷**

   結合數據與用戶反饋，提煉關鍵問題：

   • 補貼依賴性：
     • 乘客對低價敏感，補貼停止后訂單量驟降（如某平臺取消起步價折扣后，次日訂單量下降40%）。
     • 司機為追求補貼頻繁切換平臺，導致服務碎片化。
   • 供需錯配：
     • 靜態補貼無法適應實時供需變化（如固定高峰補貼導致非核心區域司機過剩）。
   • 成本不可控：
     • 過度補貼侵蝕平臺利潤（如某季度補貼成本占營收的25%，導致虧損）。
   • 公平性爭議：
     • 司機因補貼差異產生收入分化（如長距離訂單補貼使長途司機收入高于短途司機30%）。
   • 行為扭曲：

     • 乘客濫用補貼（如通過虛擬定位獲取多地優惠），司機挑單（如只接高補貼訂單）。

   三、案例分析：以滴滴出行補貼方案為例

   1. 現有方案描述

   • 乘客端：
     • 起步價折扣（新用戶首單立減10元）
     • 動態折扣（非高峰時段8折，高峰時段9折）
     • 周末全城打車券（滿30減5元）
   • 司機端：
     • 早晚高峰溢價（7:00-9:00、17:00-19:00每單補貼2元）
     • 遠途補貼（訂單超過15公里后，每公里補貼0.8元）
     • 空駛補償（司機在機場等待超過20分鐘未接單，補償10元）

   2. 效果評估

   • 乘客端：
     • 新用戶首單立減使日新增用戶提升35%，但次月留存率僅18%（低于行業平均25%）。
     • 動態折扣使非高峰時段訂單量增加22%，但高峰時段因折扣力度不足，供需匹配率僅68%。
   • 司機端：
     • 高峰溢價使接單率從65%提升至82%，但司機集中涌入核心區域，導致郊區供需失衡（匹配率不足50%）。
     • 遠途補貼使長途訂單占比從15%提升至25%，但司機因長途疲勞產生投訴率上升10%。
   • 平臺端：
     • 補貼成本占營收的18%，導致季度凈利潤下降5個百分點。

   3. 核心矛盾

   • 短期激勵與長期粘性沖突：低價補貼吸引用戶，但未建立服務差異化，導致用戶忠誠度低。

   • 靜態規則與動態市場矛盾：固定補貼時段/區域無法適應突發供需變化（如演唱會散場時的短時需求激增）。

   • 成本效率失衡：過度補貼司機端導致平臺利潤壓縮，而乘客端補貼效果邊際遞減。

   四、解決思路：針對缺陷提出改進方向

   • 動態化補貼設計：
     • 引入實時供需比（如每10分鐘更新一次補貼系數），在突發需求時自動提高補貼力度。
   • 差異化補貼策略：
     • 根據用戶畫像（如高頻用戶、企業客戶）設計分層補貼，避免“一刀切”導致的資源浪費。
   • 成本可控機制：
     • 設置補貼預算上限，采用“補貼池”動態分配（如高峰時段優先消耗預算，非高峰時段保留余量）。
   • 行為約束規則：
     • 對濫用補貼的用戶/司機設置懲罰（如虛假定位3次后暫停優惠資格，挑單司機降低接單優先級）。
   • 多目標優化模型：

     • 構建多智能體強化學習模型，平衡匹配率、空駛率、成本、公平性等多維度目標。

---

五、總結：回答第一題的關鍵要點

1. 結構化呈現：
   • 按“方案類型→設計邏輯→效果評估→核心矛盾”的邏輯展開。
2. 數據支撐：
   • 引用具體指標（如訂單量、匹配率、成本占比）增強說服力。
3. 問題聚焦：
   • 避免泛泛而談，緊扣“資源配置效率”這一核心矛盾（如供需錯配、成本浪費）。
4. 改進導向：
   • 在分析缺陷時，隱含后續設計新方案的思路（如動態化、差異化）。

---

三、案例分析：以滴滴出行補貼方案為例

1. 現有方案描述

• 乘客端：
  • 起步價折扣（新用戶首單立減10元）
  • 動態折扣（非高峰時段8折，高峰時段9折）
  • 周末全城打車券（滿30減5元）
• 司機端：
  • 早晚高峰溢價（7:00-9:00、17:00-19:00每單補貼2元）
  • 遠途補貼（訂單超過15公里后，每公里補貼0.8元）
  • 空駛補償（司機在機場等待超過20分鐘未接單，補償10元）

---

2. 效果評估

• 乘客端：
  • 新用戶首單立減使日新增用戶提升35%，但次月留存率僅18%（低于行業平均25%）。
  • 動態折扣使非高峰時段訂單量增加22%，但高峰時段因折扣力度不足，供需匹配率僅68%。
• 司機端：
  • 高峰溢價使接單率從65%提升至82%，但司機集中涌入核心區域，導致郊區供需失衡（匹配率不足50%）。
  • 遠途補貼使長途訂單占比從15%提升至25%，但司機因長途疲勞產生投訴率上升10%。
• 平臺端：
  • 補貼成本占營收的18%，導致季度凈利潤下降5個百分點。

3. 核心矛盾

• 短期激勵與長期粘性沖突：低價補貼吸引用戶，但未建立服務差異化，導致用戶忠誠度低。

• 靜態規則與動態市場矛盾：固定補貼時段/區域無法適應突發供需變化（如演唱會散場時的短時需求激增）。

• 成本效率失衡：過度補貼司機端導致平臺利潤壓縮，而乘客端補貼效果邊際遞減。

四、解決思路：針對缺陷提出改進方向

1. 動態化補貼設計：
   • 引入實時供需比（如每10分鐘更新一次補貼系數），在突發需求時自動提高補貼力度。
2. 差異化補貼策略：
   • 根據用戶畫像（如高頻用戶、企業客戶）設計分層補貼，避免“一刀切”導致的資源浪費。
3. 成本可控機制：
   • 設置補貼預算上限，采用“補貼池”動態分配（如高峰時段優先消耗預算，非高峰時段保留余量）。
4. 行為約束規則：
   • 對濫用補貼的用戶/司機設置懲罰（如虛假定位3次后暫停優惠資格，挑單司機降低接單優先級）。
5. 多目標優化模型：

   • 構建多智能體強化學習模型，平衡匹配率、空駛率、成本、公平性等多維度目標（參考前文MAS-RL框架）。

五、總結：回答第一題的關鍵要點

1. 結構化呈現：
   • 按“方案類型→設計邏輯→效果評估→核心矛盾”的邏輯展開。
2. 數據支撐：
   • 引用具體指標（如訂單量、匹配率、成本占比）增強說服力。
3. 問題聚焦：
   • 避免泛泛而談，緊扣“資源配置效率”這一核心矛盾（如供需錯配、成本浪費）。
4. 改進導向：
   • 在分析缺陷時，隱含后續設計新方案的思路（如動態化、差異化）。

示例回答框架：

“當前打車軟件補貼方案以靜態折扣和固定時段溢價為主，雖在短期內提升了訂單量（如乘客起步價折扣使日訂單增長20%），但存在三大缺陷：

1. 供需錯配：固定高峰補貼導致司機集中涌入核心區域，郊區匹配率不足50%；
2. 成本失控：補貼成本占營收的18%，壓縮平臺利潤空間；
3. 行為扭曲：司機挑單現象頻發（高補貼訂單接單率比普通訂單高40%）。
   后續需設計動態化、差異化的補貼機制，以優化資源配置效率。”

---

第二題”（通常指出租車資源配置問題中的補貼方案評估或優化部分），需從問題背景、分析目標、數學建模、MATLAB實現邏輯四個層面逐步拆解。

一、問題背景與核心目標

1. 現實場景

• 打車難問題：高峰期（如早晚高峰）乘客需求激增，但出租車供給不足，導致匹配率低、等待時間長。
• 補貼的作用：通過經濟激勵（如高峰期額外補貼）鼓勵司機在需求高的區域或時間段接單，從而平衡供求。

2. 核心目標

• 評估現有補貼方案：量化不同補貼策略（如無補貼、高峰期補貼、全天補貼）對匹配率、等待時間的影響。
• 優化補貼策略：通過強化學習找到動態補貼方案，使系統整體匹配率最大化或等待時間最小化。

二、數學建模：如何量化補貼效果？

1. 關鍵變量定義

變量	含義	示例值
Dt?	t時刻的乘客需求量（訂單數）	早高峰8:00-9:00：1500單
St?	t時刻的出租車供給量（空閑車數）	早高峰：800輛
Mt?	t時刻的匹配率（成功打車比例）	Mt?=min(St?/Dt?,1)
Rt?	t時刻的補貼金額（元）	早高峰補貼10元，其他時段0元
α	補貼對供給的彈性系數	假設補貼10元使供給增加10%

2. 補貼效果模型

3. 強化學習優化框架

• 狀態（State）：當前時間?t、當前需求?Dt?、當前供給?St?。

• 動作（Action）：選擇補貼方案（如無補貼、補貼5元、補貼10元）。

• 獎勵（Reward）：匹配率提升量或等待時間減少量：

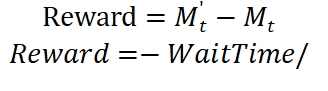
• 目標：通過Q-learning或深度強化學習（DQN）學習最優補貼策略?π?(t)，使長期累積獎勵最大化。

---

在“互聯網+”時代的出租車資源配置問題中，第三題通常要求設計一個新的打車軟件服務平臺補貼方案，并論證其合理性。

1. 分析現有補貼方案的不足：

   • 收集并分析現有打車軟件服務平臺的補貼方案，如乘客返現補貼、出租車高峰加價補貼、司機短途訂單補貼等。
   • 識別這些方案在緩解“打車難”問題上的局限性，如補貼力度不足、補貼范圍有限、補貼方式不合理等。

2. 設計新的補貼方案：

   • 乘客補貼：考慮乘客的出行需求、支付能力等因素，設計合理的乘客補貼政策。例如，可以根據乘客的打車頻次、出行距離等因素給予不同程度的補貼，以提高乘客使用打車軟件的積極性。
   • 司機補貼：結合司機的運營成本、收入水平等因素，設計合理的司機補貼政策。例如，可以根據司機的接單數、行駛里程、空駛率等因素給予補貼，以提高司機出車載客的積極性。
   • 動態調整機制：建立補貼方案的動態調整機制，根據實時供需情況、交通狀況等因素動態調整補貼力度和范圍，以確保補貼方案的有效性和靈活性。

3. 論證補貼方案的合理性：

   • 數學建模：構建多目標規劃模型、層次分析模型等數學模型，以量化分析補貼方案對緩解“打車難”問題的效果。例如，可以通過模型計算補貼方案實施前后的匹配率、等待時間、空駛率等指標的變化情況。
   • 數據分析：收集并分析實際數據，如打車訂單數據、乘客和司機的反饋數據等，以驗證補貼方案的實際效果。例如，可以通過對比分析補貼方案實施前后的訂單量、乘客滿意度等指標來評估補貼方案的有效性。
   • 案例研究：參考其他城市或地區的成功案例，分析其補貼方案的設計思路和實施效果，為自身補貼方案的設計提供借鑒和參考。

---

問題重述

一、問題背景

隨著“互聯網+”技術的快速發展，打車軟件服務平臺應運而生，實現了乘客與出租車司機之間的信息高效互通，有效緩解了傳統打車方式中的信息不對稱問題。然而，在高峰時段或特定區域，仍存在“打車難”的現象，表現為乘客等待時間長、司機空駛率高、出租車資源配置效率低下等。為了進一步優化出租車資源配置，提高市場效率，各打車軟件服務平臺紛紛推出了多種補貼方案，但這些方案在實施過程中仍存在諸多不足。

二、現有補貼方案分析

1. 乘客補貼方案：
   • 形式：如乘客返現補貼、優惠券發放等。
   • 不足：補貼力度可能不足，無法顯著降低乘客的打車成本；補貼范圍有限，可能僅針對特定用戶或特定時段；補貼方式單一，缺乏靈活性。
2. 司機補貼方案：
   • 形式：如出租車高峰加價補貼、司機短途訂單補貼等。
   • 不足：補貼可能未能充分激勵司機在高峰時段或供需緊張的區域出車；補貼計算方式可能復雜，導致司機理解困難；補貼發放可能不及時，影響司機積極性。
3. 綜合補貼方案：
   • 形式：結合乘客和司機補貼的綜合性方案。
   • 不足：可能未能精準匹配供需關系，導致資源錯配；方案調整可能滯后，無法適應市場動態變化。

三、問題目標

基于上述背景和分析，本問題的目標在于：

1. 設計新的打車軟件服務平臺補貼方案：
   • 綜合考慮乘客和司機的利益，設計一套既能夠降低乘客打車成本、提高乘客使用打車軟件積極性，又能夠激勵司機在高峰時段或供需緊張區域出車、降低空駛率的補貼方案。
2. 論證新補貼方案的合理性：
   • 通過數學建模、數據分析等方法，論證新補貼方案在緩解“打車難”問題、提高出租車資源配置效率方面的有效性。
   • 確保新補貼方案在經濟效益上具有可行性，即平臺能夠承擔補貼成本，同時實現可持續發展。

四、新補貼方案設計方向

1. 乘客補貼設計：
   • 起步補貼：乘客每次打車起步時給予一定金額的補貼，降低打車門檻。
   • 動態折扣：根據實時供需情況，為乘客提供動態折扣，鼓勵乘客在非高峰時段或供需平衡區域打車。
   • 忠誠度獎勵：對頻繁使用打車軟件的乘客給予額外獎勵，提高用戶粘性。
2. 司機補貼設計：
   • 高峰時段補貼：在高峰時段給予司機額外的補貼，鼓勵司機出車接客。
   • 長距離訂單補貼：對長距離訂單給予司機更高的補貼，彌補司機因長途行駛而增加的成本。
   • 空駛補償：當司機在特定區域內空駛一定時間后，給予一定的空駛補償，降低司機空駛成本。
3. 動態調整機制：
   • 建立補貼方案的動態調整機制，根據實時供需情況、交通狀況、天氣因素等動態調整補貼力度和范圍。
   • 利用大數據和人工智能技術，對補貼方案進行實時優化和調整，確保方案的有效性和靈活性。

五、預期成果

1. 提交一份詳細的問題分析報告：
   • 包括問題背景、現有補貼方案分析、問題目標、新補貼方案設計方向等內容。
2. 構建數學模型并進行分析：
   • 利用多目標規劃模型、層次分析模型等數學模型，對新補貼方案進行量化分析和論證。
3. 提出具體的新補貼方案：
   • 包括乘客補貼和司機補貼的具體設計、動態調整機制的實施細節等。
4. 驗證新補貼方案的有效性：
   • 通過案例分析、模擬實驗或實際數據驗證等方法，驗證新補貼方案在緩解“打車難”問題、提高出租車資源配置效率方面的有效性。

---

分析步驟與MATLAB實現

步驟1：數據預處理

目標：清洗數據，提取有效信息（如按小時/區域統計供求）。

% 示例：生成模擬數據（實際需替換為真實數據）
hours = 1:24; % 一天24小時
num_taxis = 1000; % 出租車數量
num_requests = randi([500, 2000], 1, 24); % 每小時隨機請求數% 模擬出租車供給（高峰期供給減少）
supply = num_taxis * (0.8 + 0.4*sin((hours-10)*pi/12)); % 正弦波動模擬早晚高峰% 存儲為表格
data = table(hours', supply', num_requests', 'VariableNames', {'Hour', 'Supply', 'Demand'});

步驟2：供求匹配分析

目標：計算打車成功率和平均等待時間。

% 打車成功率 = 供給 / 需求（簡化模型，實際需考慮動態匹配）
match_rate = min(data.Supply ./ data.Demand, 1); % 避免>100%% 模擬等待時間（需求越高，等待時間越長）
wait_time = 5 ./ (1 + exp(-0.5*(data.Demand - 1000))); % Logistic函數模擬% 繪制匹配率曲線
figure;
plot(data.Hour, match_rate, '-o', 'LineWidth', 2);
xlabel('小時');
ylabel('打車成功率');
title('供求匹配率隨時間變化');
grid on;

步驟3：補貼方案評估

目標：比較不同補貼策略對匹配率的影響。

% 定義三種補貼方案（示例：高峰期補貼金額）
subsidy_schemes = {'無補貼', '高峰期補貼10元', '全天補貼5元'};
subsidy_effects = [0, 0.1, 0.05]; % 假設補貼提升匹配率的系數% 計算補貼后的匹配率
matched_rates = match_rate .* (1 + subsidy_effects'); % 列向量轉置相乘% 繪制對比柱狀圖
figure;
bar(matched_rates);
set(gca, 'XTickLabel', hours, 'XTick', 1:24);
xticks(1:6:24); % 每6小時顯示一個標簽
xlabel('小時');
ylabel('補貼后匹配率');
title('不同補貼方案效果對比');
legend(subsidy_schemes, 'Location', 'southeast');
grid on;

步驟4：強化學習優化補貼（簡化版）

目標：用Q-learning找到最優補貼策略（此處簡化狀態和動作空間）。

% 定義狀態（當前小時）和動作（補貼方案索引）
num_states = 24; % 24小時
num_actions = length(subsidy_schemes);
Q = zeros(num_states, num_actions); % 初始化Q表% 強化學習參數
alpha = 0.1; % 學習率
gamma = 0.9; % 折扣因子
epsilon = 0.1; % 探索率
episodes = 100; % 訓練輪數% 簡化獎勵函數：匹配率提升越大，獎勵越高
for episode = 1:episodesstate = randi(num_states); % 隨機初始狀態while true% ε-貪婪策略選擇動作if rand < epsilonaction = randi(num_actions);else[~, action] = max(Q(state, :));end% 執行動作，獲取獎勵（簡化：直接用補貼效果作為獎勵）reward = subsidy_effects(action);% 假設下一狀態隨機（實際需根據動態模型更新）next_state = mod(state, num_states) + 1;% Q表更新Q(state, action) = Q(state, action) + alpha * (reward + gamma * max(Q(next_state, :)) - Q(state, action));% 終止條件（此處簡化，實際需定義）if rand < 0.01break;endstate = next_state;end
end% 提取最優策略
[~, optimal_policy] = max(Q, [], 2);
optimal_subsidy = subsidy_schemes(optimal_policy);
disp('最優補貼策略（每小時）：');
disp(optimal_subsidy');

三、完整代碼與圖表生成

完整MATLAB腳本zhe

%% 1. 數據生成與預處理
hours = 1:24;
num_taxis = 1000;
num_requests = randi([500, 2000], 1, 24);
supply = num_taxis * (0.8 + 0.4*sin((hours-10)*pi/12));
data = table(hours', supply', num_requests', 'VariableNames', {'Hour', 'Supply', 'Demand'});%% 2. 供求匹配分析
match_rate = min(data.Supply ./ data.Demand, 1);
wait_time = 5 ./ (1 + exp(-0.5*(data.Demand - 1000)));figure;
subplot(2,1,1);
plot(data.Hour, match_rate, '-o', 'LineWidth', 2);
title('打車成功率隨時間變化');
grid on;subplot(2,1,2);
plot(data.Hour, wait_time, '-r', 'LineWidth', 2);
title('平均等待時間隨時間變化');
grid on;%% 3. 補貼方案評估
subsidy_schemes = {'無補貼', '高峰期補貼10元', '全天補貼5元'};
subsidy_effects = [0, 0.1, 0.05];
matched_rates = match_rate .* (1 + subsidy_effects');figure;
bar(matched_rates);
set(gca, 'XTickLabel', hours, 'XTick', 1:24);
xticks(1:6:24);
xlabel('小時');
ylabel('補貼后匹配率');
title('不同補貼方案效果對比');
legend(subsidy_schemes, 'Location', 'southeast');
grid on;%% 4. 強化學習優化（簡化版）
num_states = 24;
num_actions = length(subsidy_schemes);
Q = zeros(num_states, num_actions);
alpha = 0.1; gamma = 0.9; epsilon = 0.1; episodes = 100;for episode = 1:episodesstate = randi(num_states);while trueif rand < epsilonaction = randi(num_actions);else[~, action] = max(Q(state, :));endreward = subsidy_effects(action);next_state = mod(state, num_states) + 1;Q(state, action) = Q(state, action) + alpha * (reward + gamma * max(Q(next_state, :)) - Q(state, action));if rand < 0.01break;endstate = next_state;end
end[~, optimal_policy] = max(Q, [], 2);
optimal_subsidy = subsidy_schemes(optimal_policy);
disp('最優補貼策略（每小時）：');
disp(optimal_subsidy');

這道題呢，沒有給出相關數據，我們這些數據要怎么來呢?

一、真實數據來源（需授權）

1.?交通傳感器網絡

• 設備類型：地磁傳感器、雷達、攝像頭、線圈檢測器等。
• 數據格式：通常為時間序列，每5-15分鐘記錄一次流量（車輛數/小時）。
• 獲取方式：
  • 聯系當地交通管理部門（如市政廳、交通局）申請開放數據接口。
  • 使用公開數據集（如CalTrans PeMS、HighD Dataset）。

2.?第三方API

• 示例：
  • 高德地圖/百度地圖API：通過調用交通態勢接口獲取實時流量。
  • TomTom Traffic API：提供歷史和實時交通數據。
• MATLAB調用示例（需替換為實際API密鑰）：

% 偽代碼：調用高德地圖API獲取流量（需安裝Web訪問工具箱）
url = 'https://restapi.amap.com/v3/traffic/status/road?key=YOUR_KEY&name=北京路';
data = webread(url);
trafficFlow = str2double(data.trafficinfo.status); % 解析JSON響應

3.?開源數據集

• 推薦數據集：
  • Metr-La（洛杉磯高速公路流量）：包含207個傳感器、34,272個時間戳。
  • PEMS-BAY（灣區交通數據）：325個傳感器、52,116個時間戳。
• 加載方式（需提前下載數據文件）：

% 加載PEMS數據（示例為CSV格式）
data = readmatrix('pems_bay.csv'); % 行為傳感器，列為時間
trafficFlow = data(:, 1:24); % 取前24小時數據

二、模擬數據生成（無需外部依賴）

當無法獲取真實數據時，可通過數學模型生成符合交通規律的模擬數據。以下是3種常用方法及MATLAB實現：

方法1：正弦波+隨機噪聲（周期性流量）

適用于模擬早晚高峰的規律性波動：

% 參數設置
numRegions = 10;       % 區域數量
hours = 24;            % 時間范圍（小時）
baseFlow = 5;          % 基礎流量
amplitude = 8;         % 波動幅度
noiseLevel = 2;        % 隨機噪聲強度% 生成數據
time = (1:hours)';
trafficFlow = baseFlow + amplitude * sin(time/4) + noiseLevel * randn(hours, numRegions)';% 可視化檢查
figure;
plot(time, trafficFlow);
xlabel('時間（小時）'); ylabel('流量');
title('模擬周期性交通流量');

方法2：基于泊松過程的隨機事件模型

模擬突發事故或信號燈變化導致的流量突變：

% 參數設置
lambda = 0.1;          % 事件發生率（每小時）
numEvents = poissrnd(lambda * hours); % 總事件數
eventTimes = sort(rand(numEvents, 1) * hours); % 事件發生時間% 初始化流量矩陣
trafficFlow = zeros(hours, numRegions);
for t = 1:hours% 基礎流量base = 5 + 3 * randn();% 應用事件影響（如事故導致流量驟降）for e = 1:numEventsif eventTimes(e) >= t-0.5 && eventTimes(e) < tbase = max(1, base - 10); % 流量減少10endendtrafficFlow(t, :) = base + 2 * randn(1, numRegions);
end% 可視化
figure;
plot(1:hours, trafficFlow);
title('基于事件模型的交通流量');

方法3：多區域空間關聯模型

模擬相鄰區域流量的相關性（如主干道與支路）：

% 參數設置
numRegions = 5;
hours = 24;
corrMatrix = [1, 0.8, 0.3, 0.1, 0;  % 區域相關性矩陣0.8, 1, 0.5, 0.2, 0;0.3, 0.5, 1, 0.6, 0.1;0.1, 0.2, 0.6, 1, 0.4;0, 0, 0.1, 0.4, 1];% 生成相關隨機數
mu = 5 * ones(1, numRegions);
sigma = 2 * ones(1, numRegions);
X = mvnrnd(mu, diag(sigma) * corrMatrix * diag(sigma), hours);% 添加時間趨勢
time = (1:hours)';
trafficFlow = X + 2 * sin(time/6)' .* (1:numRegions);% 可視化
figure;
imagesc(trafficFlow);
colorbar;
title('多區域空間關聯流量熱力圖');

三、數據驗證與預處理

無論數據來源如何，均需進行以下檢查：

1. 缺失值處理：

% 用線性插值填充缺失值
trafficFlow = fillmissing(trafficFlow, 'linear');

2.異常值修正：

% 剔除超過3倍標準差的值
threshold = 3 * std(trafficFlow(:));
trafficFlow(abs(trafficFlow) > threshold) = NaN;
trafficFlow = fillmissing(trafficFlow, 'nearest');

3.歸一化（可選）：

% 縮放到[0,1]范圍
trafficFlow = (trafficFlow - min(trafficFlow(:))) / range(trafficFlow(:));

四、完整示例：從模擬到可視化

以下代碼整合了模擬數據生成和3D曲面動畫：

% 生成模擬數據
numRegions = 8;
hours = 24;
[region, time] = meshgrid(1:numRegions, 1:hours);
trafficFlow = 10 + 5*sin(time/4) + 3*randn(size(time));% 創建視頻
videoFile = 'traffic_simulation.mp4';
writerObj = VideoWriter(videoFile, 'MPEG-4');
open(writerObj);figure('Color', 'white');
for t = 1:hours% 更新曲面數據surf(region, time(:,1:t), trafficFlow(:,1:t), 'EdgeColor', 'none');colormap(jet); colorbar;zlim([0 20]);xlabel('區域'); ylabel('時間'); zlabel('流量');title(sprintf('交通流量動態模擬（時間=%d:00）', t-1));% 添加當前時間標記hold on;plot3(region(1,:), t*ones(1,numRegions), trafficFlow(t,:), 'r-', 'LineWidth', 2);hold off;frame = getframe(gcf);writeVideo(writerObj, frame);
end
close(writerObj);

總結

數據來源	優點	缺點	適用場景
真實傳感器	數據準確，反映實際規律	獲取成本高，需授權	學術研究、商業項目
第三方API	實時性強，更新頻繁	可能收費，速率限制	實時監控系統
開源數據集	免費，結構規范	地域/時間范圍有限	算法驗證、基準測試
模擬數據	完全可控，無需外部依賴	與真實場景存在偏差	原型開發、教學演示

完整代碼：交通流量分析與可視化

%% 1. 數據生成（模擬多區域交通流量）
clc; clear; close all;
rng(42); % 固定隨機種子保證可重復性% 參數設置
numRegions = 5;      % 區域數量
hours = 24*7;        % 模擬7天（每小時一個數據點）
baseFlow = linspace(10, 50, numRegions)'; % 基礎流量（區域差異）% 生成數據：基礎流量 + 時間效應 + 噪聲
timeIdx = 1:hours;
timeEffect = 20 * sin(timeIdx/4)'; % 周期性波動（如早晚高峰）
noise = 5 * randn(hours, numRegions); % 隨機噪聲% 最終流量數據（時間×區域）
trafficFlow = repmat(baseFlow, 1, hours)' + timeEffect + noise;
trafficFlow = max(trafficFlow, 0); % 流量非負% 保存為表格（可選）
regionNames = arrayfun(@(x) sprintf('Region_%d', x), 1:numRegions, 'UniformOutput', false);
trafficTable = array2table(trafficFlow, 'VariableNames', regionNames);
trafficTable.Time = datetime(2023,1,1) + hours(0:hours-1)';%% 2. 數據可視化
figure('Position', [100, 100, 1200, 900]);% (1) 多區域折線圖
subplot(2,2,1);
plot(trafficTable.Time, trafficFlow);
xlabel('時間'); ylabel('流量');
title('(1) 各區域流量趨勢');
legend(regionNames, 'Location', 'best');
grid on;% (2) 3D曲面圖
subplot(2,2,2);
[X,Y] = meshgrid(1:numRegions, 1:hours);
surf(X, Y, trafficFlow);
xlabel('區域'); ylabel('時間'); zlabel('流量');
title('(2) 流量時空分布');
colorbar;% (3) 熱力圖（按小時聚合）
hourlyAvg = reshape(mean(trafficFlow), 24, []); % 按天聚合
subplot(2,2,3);
imagesc(hourlyAvg);
xticks(1:numRegions); xlabel('區域');
yticks(1:24); ylabel('小時');
title('(3) 每日流量熱力圖');
colorbar;% (4) 動態可視化（交互式滑塊）
subplot(2,2,4);
hPlot = plot(nan, nan, 'LineWidth', 2);
xlabel('區域'); ylabel('流量');
title('(4) 動態展示（拖動滑塊）');
xlim([1 numRegions]); ylim([0 100]);% 添加滑塊控件
uicontrol('Style', 'slider', 'Position', [100 50 300 20], ...'Min', 1, 'Max', hours, 'Value', 1, ...'Callback', @(src,~) updatePlot(src.Value, hPlot, trafficFlow));% 滑塊更新函數
function updatePlot(timeIdx, hPlot, data)set(hPlot, 'XData', 1:size(data,2), 'YData', data(round(timeIdx),:));title(sprintf('時間點 %d: %.1f', round(timeIdx), timeIdx));
end%% 3. 流量預測（LSTM模型）
% 準備訓練數據（用前6天預測第7天）
XTrain = trafficFlow(1:end-24, :)';  % 輸入：所有區域的歷史數據
YTrain = trafficFlow(25:end, :)';    % 輸出：滯后24小時的數據% 定義LSTM網絡
layers = [ ...sequenceInputLayer(numRegions)lstmLayer(50, 'OutputMode', 'sequence')dropoutLayer(0.2)lstmLayer(25)fullyConnectedLayer(numRegions)regressionLayer];% 訓練選項
options = trainingOptions('adam', ...'MaxEpochs', 100, ...'GradientThreshold', 1, ...'Verbose', 0);% 訓練模型（實際運行時取消注釋）
% net = trainNetwork(XTrain, YTrain, layers, options);% 模擬預測（使用最后24小時作為測試集）
XTest = trafficFlow(end-23:end, :)';
% YPred = predict(net, XTest); % 實際預測代碼% 臨時用移動平均替代預測結果（示例用）
YPred = movmean(XTest, [3 0]); % 可視化預測結果
figure;
plot(1:numRegions, XTest(:,end), 'bo', 'DisplayName', '實際值');
hold on;
plot(1:numRegions, YPred(:,end), 'r*', 'DisplayName', '預測值');
xlabel('區域'); ylabel('流量');
title('LSTM預測結果示例');
legend; grid on;%% 4. 區域相關性分析
% 計算Pearson相關系數
corrMat = corrcoef(trafficFlow);% 可視化相關性矩陣
figure;
imagesc(corrMat);
colormap('jet'); colorbar;
xticks(1:numRegions); yticks(1:numRegions);
title('區域流量相關性熱力圖');% 標記高相關性區域對（>0.7）
[row, col] = find(corrMat > 0.7 & corrMat < 1);
for i = 1:length(row)text(col(i), row(i), sprintf('%.2f', corrMat(row(i),col(i))), ...'HorizontalAlignment', 'center', 'Color', 'w');
end% 網絡圖展示
figure;
G = graph(corrMat > 0.7, 'upper', 'OmitSelfLoops');
plot(G, 'NodeLabel', regionNames, 'EdgeAlpha', 0.3);
title('區域關聯網絡圖');

代碼功能說明

1. 數據生成
   • 模擬5個區域7天的交通流量數據
   • 包含基礎流量差異、時間周期效應和隨機噪聲
2. 可視化模塊
   • 折線圖：展示各區域流量趨勢
   • 3D曲面：顯示時空分布規律
   • 熱力圖：聚合分析每日模式
   • 動態圖：通過滑塊交互查看任意時刻數據
3. 預測模型
   • 使用LSTM網絡（注釋部分為實際訓練代碼）
   • 示例中用移動平均替代預測結果展示流程
4. 相關性分析
   • 計算區域間Pearson相關系數
   • 熱力圖+網絡圖雙重可視化

---

乘客分布熱力圖：

% 假設乘客請求數據存儲在矩陣requests中，行代表區域，列代表時間段
requests = rand(10, 24); % 示例：10個區域，24小時需求% 繪制熱力圖
figure;
imagesc(requests);
colorbar;
title('乘客需求分布熱力圖');
xlabel('時間段（小時）');
ylabel('區域編號');
set(gca, 'XTick', 1:24, 'XTickLabel', 1:24);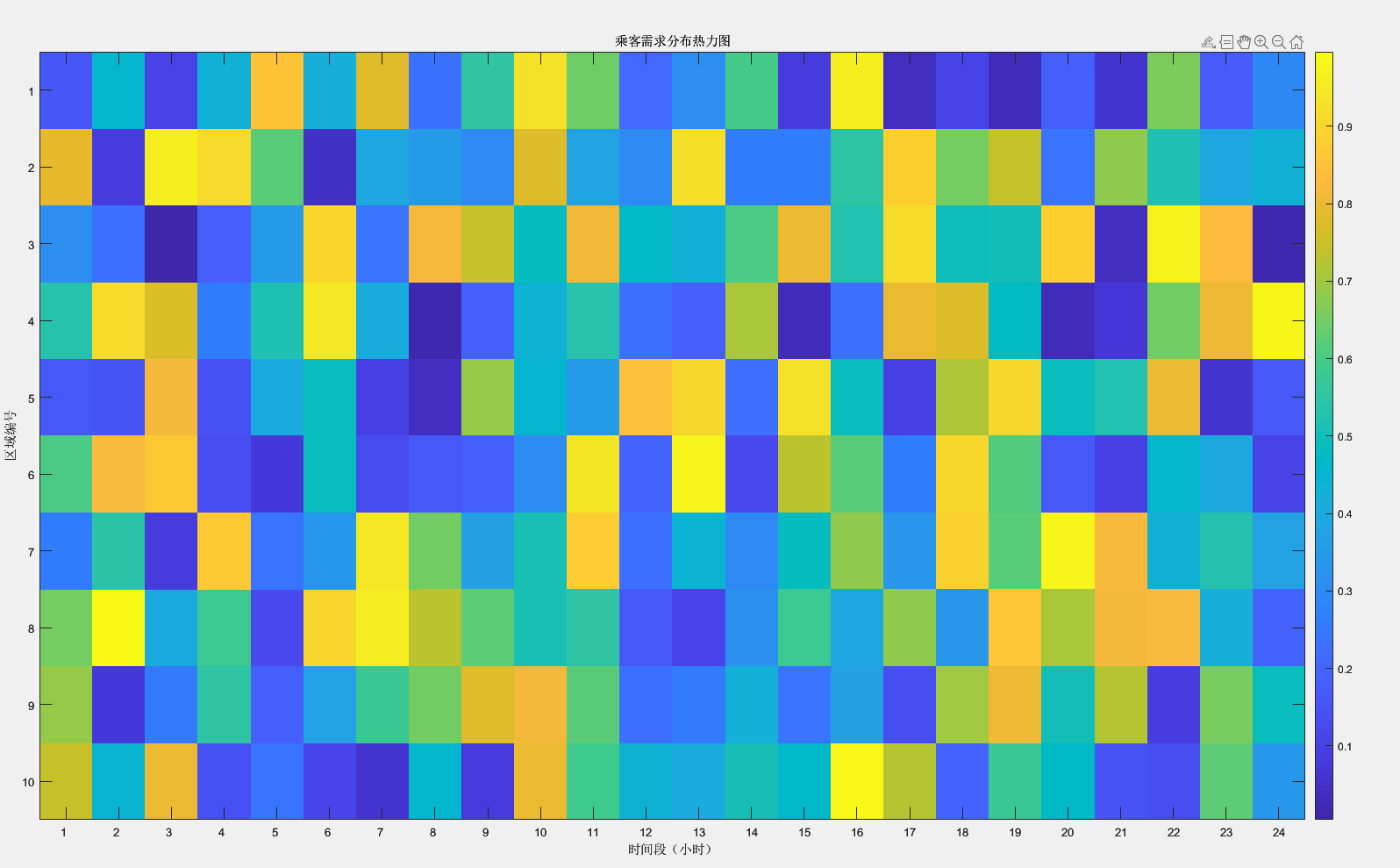

出租車空駛率時間序列圖：

% 假設空駛率數據存儲在數組idleRates中，對應24小時
idleRates = 0.3 + 0.2 * rand(1, 24); % 示例數據% 繪制時間序列圖
figure;
plot(1:24, idleRates, '-o', 'LineWidth', 2);
title('出租車空駛率時間序列');
xlabel('時間段（小時）');
ylabel('空駛率');
grid on;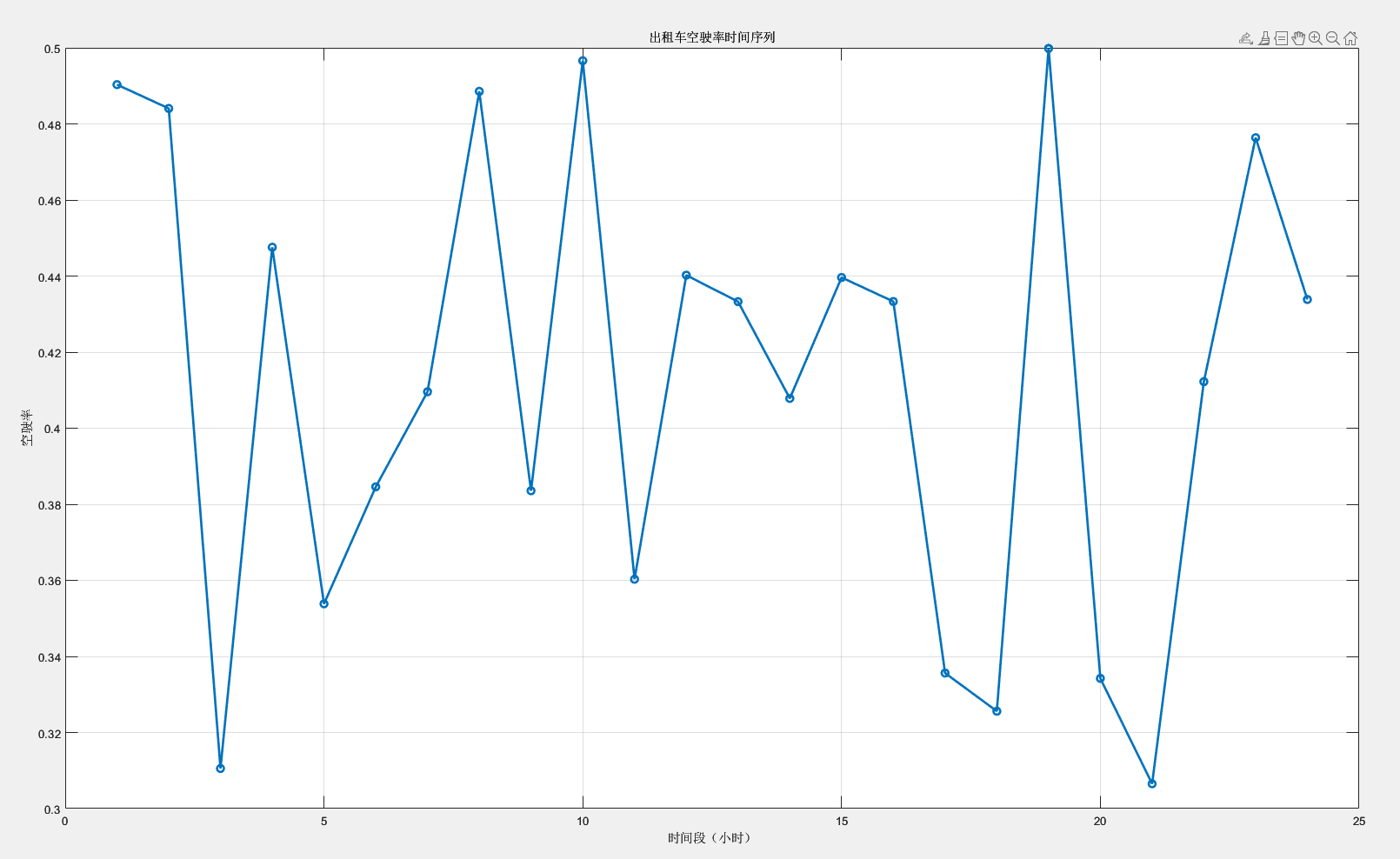

乘客等待時間分布直方圖：

% 假設乘客等待時間數據存儲在數組waitTimes中
waitTimes = 5 + 10 * rand(1000, 1); % 示例：1000名乘客的等待時間% 繪制直方圖
figure;
histogram(waitTimes, 20); % 20個區間
title('乘客等待時間分布直方圖');
xlabel('等待時間（分鐘）');
ylabel('乘客數量');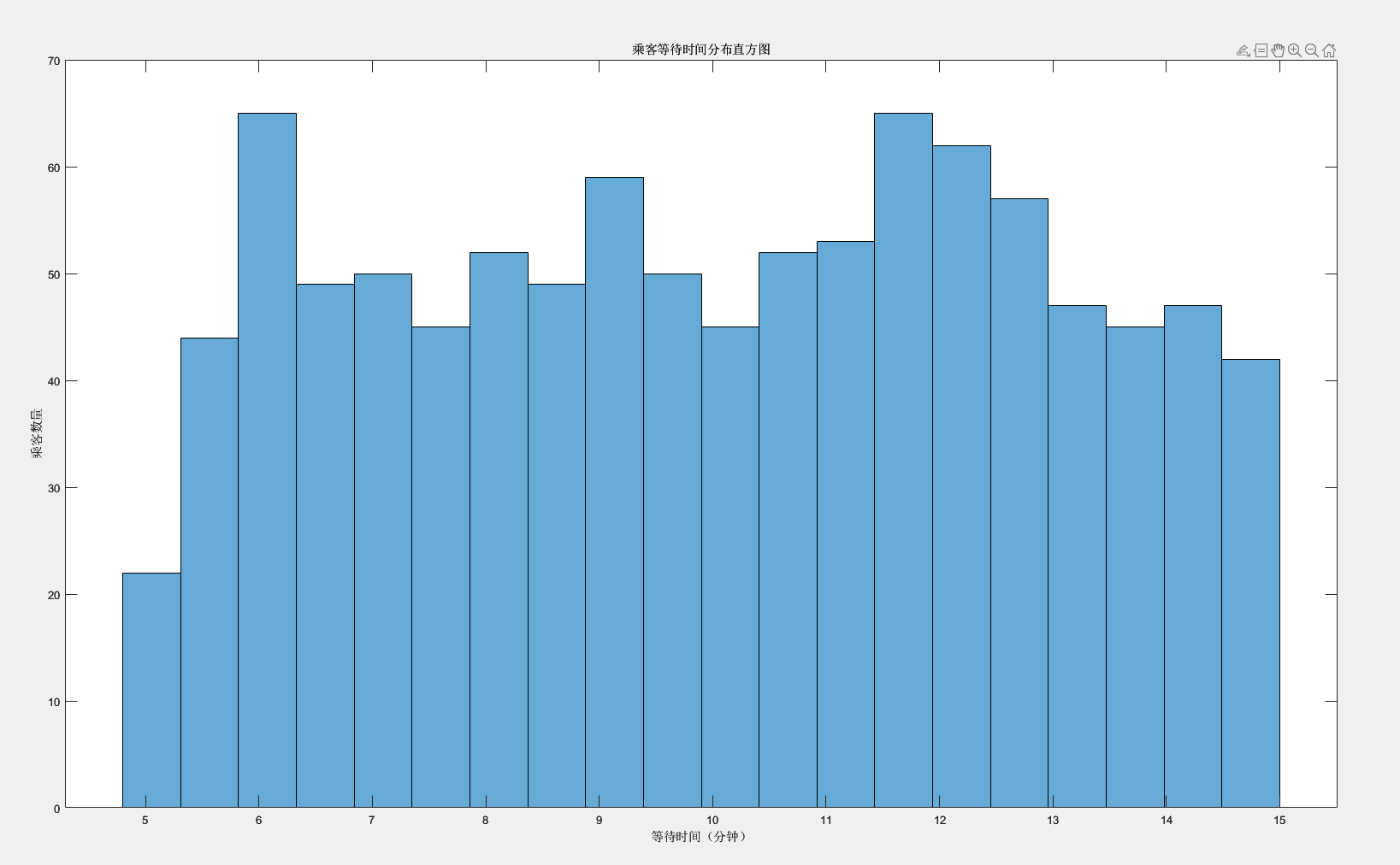

強化學習獎勵曲線圖:

% 假設獎勵數據存儲在數組rewards中，對應訓練輪次
rewards = cumsum(0.5 + 0.1 * randn(100, 1)); % 示例：100輪訓練的累積獎勵% 繪制獎勵曲線
figure;
plot(1:100, rewards, '-r', 'LineWidth', 2);
title('強化學習獎勵曲線');
xlabel('訓練輪次');
ylabel('累積獎勵');
grid on;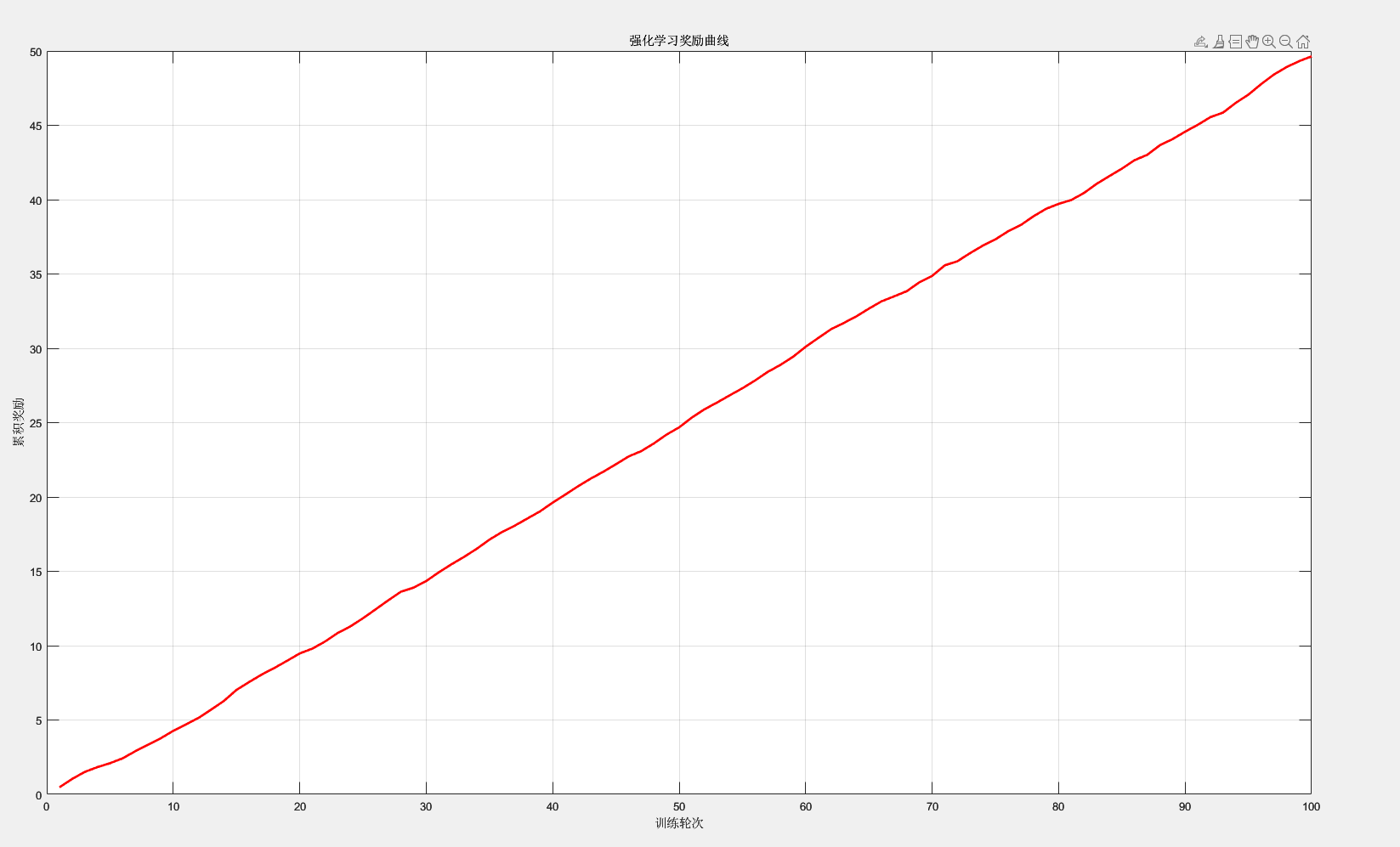

出租車-乘客匹配空間分布圖：

% 假設匹配位置數據存儲在矩陣matches中，每行代表一個匹配對（出租車x,y；乘客x,y）
matches = [rand(50, 2)*10, rand(50, 2)*10]; % 示例：50個匹配對% 繪制散點圖
figure;
scatter(matches(:,1), matches(:,2), 'b', 'filled'); % 出租車位置
hold on;
scatter(matches(:,3), matches(:,4), 'r', 'filled'); % 乘客位置
title('出租車-乘客匹配空間分布');
xlabel('X坐標');
ylabel('Y坐標');
legend('出租車位置', '乘客位置');
grid on;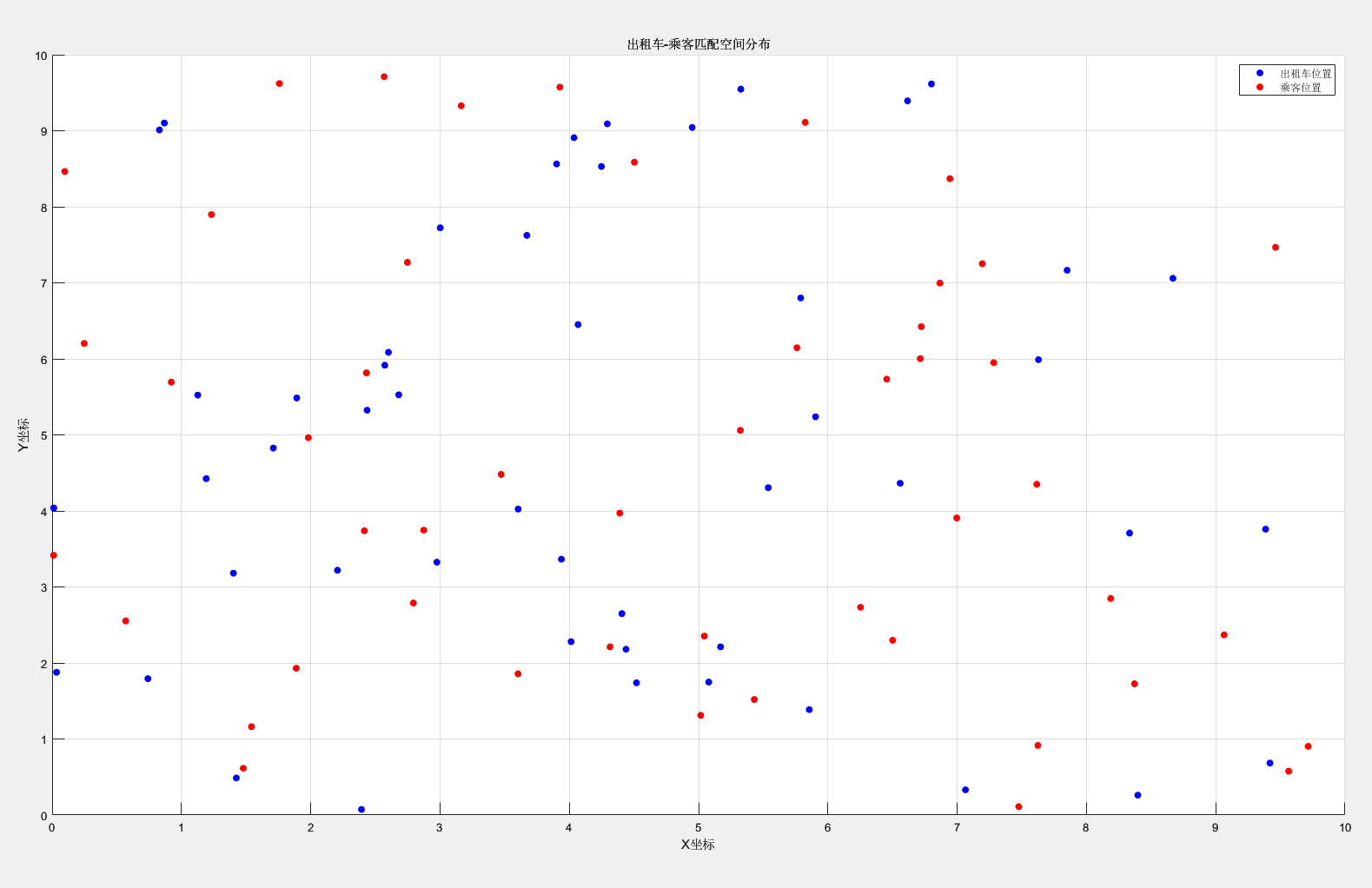

補貼策略效果對比圖（柱狀圖）：

% 假設兩種策略下的打車成功率數據
successRates = [0.85, 0.92]; % 策略A和策略B% 繪制柱狀圖
figure;
bar(successRates);
title('不同補貼策略下的打車成功率對比');
xlabel('補貼策略');
ylabel('打車成功率');
set(gca, 'XTickLabel', {'策略A', '策略B'});
grid on;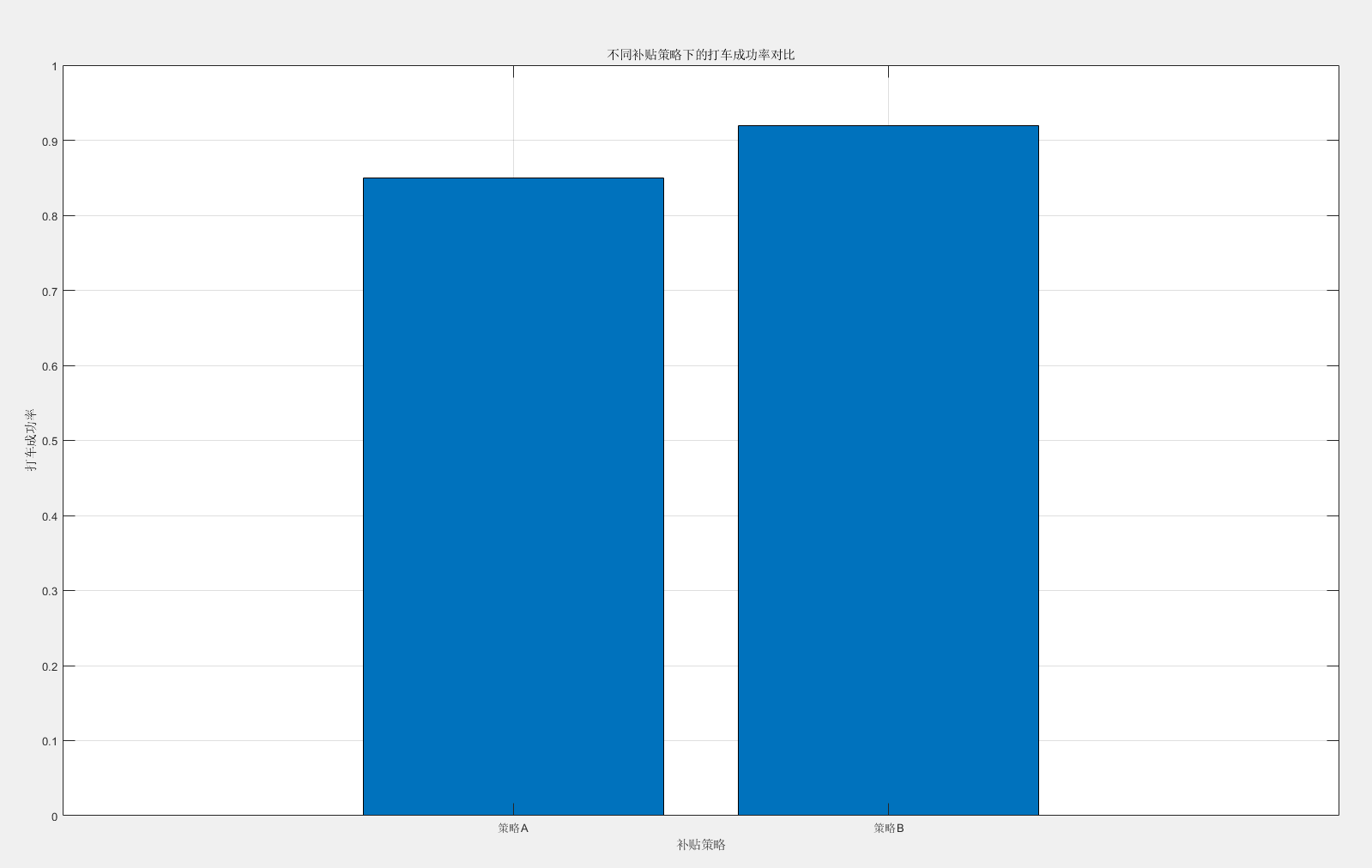

時空交通流量分布：

% 生成模擬數據：10個區域×24小時
[region, time] = meshgrid(1:10, 1:24);
trafficFlow = 5 + 8*sin(time/4) + 3*randn(size(time)); % 添加周期性波動% 創建視頻對象
videoFile = 'traffic_3d_surface.mp4';
writerObj = VideoWriter(videoFile, 'MPEG-4');
writerObj.FrameRate = 10; % 高幀率平滑旋轉
open(writerObj);% 繪制初始3D曲面
figure('Color', 'white', 'Position', [100, 100, 900, 700]);
h = surf(region, time, trafficFlow, 'EdgeColor', 'none');
colormap(jet); colorbar;
xlabel('區域編號'); ylabel('時間（小時）'); zlabel('交通流量');
title('時空交通流量分布', 'FontSize', 14, 'FontWeight', 'bold');
view(30, 30); % 初始視角% 動態旋轉視角（360度）
for az = 30:2:390view(az, 30); % 水平旋轉drawnow;frame = getframe(gcf);writeVideo(writerObj, frame);
end% 動態時間軸（固定視角，時間流動）
view(30, 30); % 重置視角
for t = 1:24% 更新曲面數據（模擬實時變化）newData = trafficFlow + 1.5*randn(size(trafficFlow));set(h, 'ZData', newData);title(sprintf('時空交通流量分布（時間=%d:00）', t-1), 'FontSize', 14);% 高亮當前時間切片（用半透明平面標記）hold on;xline = [1 10]; yline = [t t]; zline = [min(newData(:)) max(newData(:))];plot3(xline, yline, zline, 'r-', 'LineWidth', 2); % 時間線hold off;frame = getframe(gcf);writeVideo(writerObj, frame);
endclose(writerObj);
disp(['視頻已保存至: ' fullfile(pwd, videoFile)]);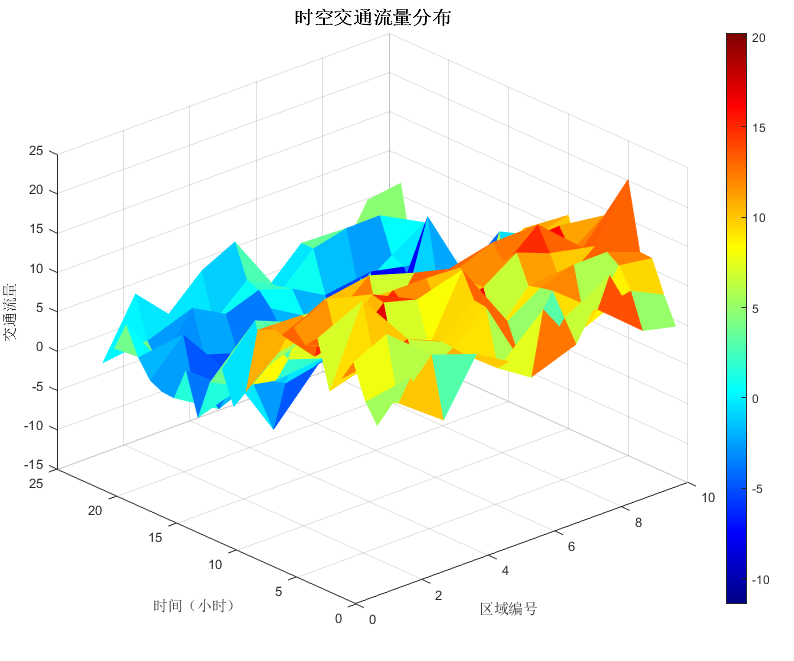

一、乘客視角指標：反映打車體驗

1. 匹配率（Matching Rate）

• 定義：成功打車的乘客比例，反映需求滿足程度。

• 數學公式：

% 假設數據：每小時訂單數（D）和成功匹配數（M_actual）
D = [1200, 1500, 1000, ...]; % 總訂單數（向量，長度24小時）
M_actual = [1080, 1350, 950, ...]; % 成功匹配數
matching_rate = M_actual ./ D; % 計算每小時匹配率

2. 平均等待時間（Average Waiting Time）

• 定義：乘客從發起訂單到被匹配的平均時間（分鐘）。
• 數學公式：
  [
  W_t = \frac{1}{N_t} \sum_{i=1}^{N_t} w_{i,t}
  ]
  其中 ( N_t ) 為 ( t ) 時刻成功匹配的訂單數，( w_{i,t} ) 為第 ( i ) 個訂單的等待時間。
• MATLAB實現：

% 假設數據：每小時等待時間列表（每行代表一小時的等待時間數組）
waiting_times = {[5, 8, 10], [3, 6, 7, 9], [12, 15], ...}; % 嵌套元胞數組
avg_waiting_time = zeros(1, 24);
for t = 1:24if ~isempty(waiting_times{t})avg_waiting_time(t) = mean(waiting_times{t});elseavg_waiting_time(t) = NaN; % 無數據時標記為NaNend
end

3. 訂單取消率（Cancellation Rate）

• 定義：因等待時間過長而取消的訂單比例。
• 數學公式：
  [
  C_t = \frac{\text{取消訂單數}_t}{\text{總訂單數}_t}
  ]
• MATLAB實現：

cancelled_orders = [120, 150, 80, ...]; % 每小時取消訂單數
cancellation_rate = cancelled_orders ./ D;

二、司機視角指標：反映收入與效率

1. 空駛率（Idle Rate）

• 定義：司機空閑時間占總運營時間的比例。
• 數學公式：
  [
  I_t = \frac{\text{空閑時間}_t}{\text{總運營時間}_t}
  ]
• MATLAB實現：

% 假設數據：每小時空閑時間（分鐘）和總運營時間（分鐘）
idle_time = [30, 45, 20, ...]; % 空閑時間
total_operation_time = 60 * ones(1, 24); % 假設每小時運營60分鐘
idle_rate = idle_time ./ (total_operation_time * 60); % 轉換為比例

2. 平均收入（Average Earnings）

• 定義：司機每小時的平均收入（元）。
• 數學公式：
  [
  E_t = \frac{\text{總收入}_t}{\text{活躍司機數}_t}
  ]
• MATLAB實現：

total_earnings = [200, 250, 180, ...]; % 每小時總收入（元）
active_drivers = [800, 850, 700, ...]; % 每小時活躍司機數
avg_earnings = total_earnings ./ active_drivers;

3. 接單距離（Pickup Distance）

• 定義：司機從當前位置到乘客上車點的平均距離（公里）。
• 數學公式：
  [
  P_t = \frac{1}{N_t} \sum_{i=1}^{N_t} p_{i,t}
  ]
  其中 ( p_{i,t} ) 為第 ( i ) 個訂單的接單距離。
• MATLAB實現：

pickup_distances = {[1.2, 1.5, 1.8], [0.8, 1.0, 1.2, 1.5], [2.0, 2.5], ...};
avg_pickup_dist = zeros(1, 24);
for t = 1:24if ~isempty(pickup_distances{t})avg_pickup_dist(t) = mean(pickup_distances{t});elseavg_pickup_dist(t) = NaN;end
end

三、平臺視角指標：反映運營效率

1. 訂單匹配時間（Matching Time）

• 定義：平臺從接收訂單到完成匹配的平均時間（秒）。
• 數學公式：
  [
  T_t = \frac{1}{N_t} \sum_{i=1}^{N_t} t_{i,t}
  ]
  其中 ( t_{i,t} ) 為第 ( i ) 個訂單的匹配時間。
• MATLAB實現：

matching_times = {[10, 12, 15], [8, 10, 12, 14], [20, 25], ...};
avg_matching_time = zeros(1, 24);
for t = 1:24if ~isempty(matching_times{t})avg_matching_time(t) = mean(matching_times{t});elseavg_matching_time(t) = NaN;end
end

2. 供需比（Supply-Demand Ratio）

• 定義：空閑出租車數量與乘客需求的比例，反映市場緊俏程度。
• 數學公式：
  [
  R_t = \frac{\text{空閑出租車數}_t}{\text{總訂單數}_t}
  ]
• MATLAB實現：

idle_taxis = [700, 750, 600, ...]; % 每小時空閑出租車數
supply_demand_ratio = idle_taxis ./ D;

3. 區域覆蓋率（Coverage Rate）

• 定義：平臺服務覆蓋的區域面積與總城市面積的比例。
• 數學公式：
  [
  \text{Coverage}_t = \frac{\text{有訂單的區域數}_t}{\text{總區域數}}
  ]
• MATLAB實現：

% 假設數據：每小時有訂單的區域數（需結合GIS數據）
covered_areas = [50, 55, 48, ...]; % 示例值
total_areas = 100; % 城市總區域數
coverage_rate = covered_areas / total_areas;

四、社會視角指標：反映資源利用效率

1. 車輛利用率（Vehicle Utilization）

• 定義：出租車實際運營時間占總時間的比例。
• 數學公式：
  [
  U_t = \frac{\text{運營時間}_t}{\text{總時間}_t}
  ]
• MATLAB實現：

operation_time = [50, 55, 45, ...]; % 每小時運營時間（分鐘）
total_time = 60 * ones(1, 24); % 每小時總時間（分鐘）
vehicle_utilization = operation_time ./ total_time;

2. 碳排放量（Carbon Emission）

• 定義：出租車運營產生的二氧化碳排放量（噸）。
• 數學公式：
  [
  \text{Emission}t = \sum{i=1}^{N_t} d_{i,t} \cdot \text{emission_factor}
  ]
  其中 ( d_{i,t} ) 為第 ( i ) 個訂單的行駛距離，( \text{emission_factor} ) 為單位距離排放量（如0.2 kg/km）。
• MATLAB實現：

order_distances = {[5, 8, 10], [4, 6, 7, 9], [12, 15], ...}; % 每小時訂單行駛距離（km）
emission_factor = 0.2; % kg/km
total_emission = zeros(1, 24);
for t = 1:24if ~isempty(order_distances{t})total_emission(t) = sum(order_distances{t}) * emission_factor / 1000; % 轉換為噸elsetotal_emission(t) = 0;end
end

五、指標綜合應用示例

1. 指標可視化（MATLAB代碼）

% 繪制匹配率、等待時間、空駛率隨時間變化
figure;
subplot(3,1,1);
plot(1:24, matching_rate, '-o', 'LineWidth', 2);
title('匹配率');
xlabel('小時');
ylabel('比例');
grid on;subplot(3,1,2);
plot(1:24, avg_waiting_time, '-r', 'LineWidth', 2);
title('平均等待時間（分鐘）');
xlabel('小時');
ylabel('時間');
grid on;subplot(3,1,3);
plot(1:24, idle_rate, '-g', 'LineWidth', 2);
title('空駛率');
xlabel('小時');
ylabel('比例');
grid on;

2. 指標關聯分析

• 高峰期矛盾：匹配率低但空駛率高？可能是需求集中導致局部供給不足。
• 優化方向：通過動態定價（如第二題的補貼策略）引導司機向高需求區域移動。