題目鏈接
LeetCode兩數之和
題目描述
題目解析
注意：前提條件：輸入的數組numbers是已排序的。
核心思路：雙指針法
利用數組已排序的特性，通過兩個指針從兩端向中間移動，快速定位符合條件的兩個數，時間復雜度為O(n)（n 為數組長度），空間復雜度為O(1)，比哈希表解法更優。
具體步驟：
-
初始化指針：
left指針指向數組起始位置（下標 0）。right指針指向數組末尾位置（下標numbers.size()-1）。
-
循環查找目標和：
- 計算兩指針指向元素的和
sum = numbers[left] + numbers[right]。 - 若
sum > target：說明右側元素過大，將right指針左移（right--），減小總和。 - 若
sum < target：說明左側元素過小，將left指針右移（left++），增大總和。 - 若
sum == target：找到符合條件的兩個元素，返回它們的下標（注意 + 1，因為題目要求從 1 開始計數）。
- 計算兩指針指向元素的和
-
邊界處理：
- 若循環結束仍未找到（理論上題目保證有解，此步可省略），返回
{-1, -1}。
- 若循環結束仍未找到（理論上題目保證有解，此步可省略），返回
示例說明：
假設輸入：numbers = [2, 7, 11, 15]，target = 9。
- 初始
left=0（值 2），right=3（值 15），sum=17 > 9?→?right--（指向 11）。 - 新
sum=2+11=13 > 9?→?right--（指向 7）。 - 新
sum=2+7=9 == target?→ 返回{0+1, 1+1} = {1, 2}。
完整代碼
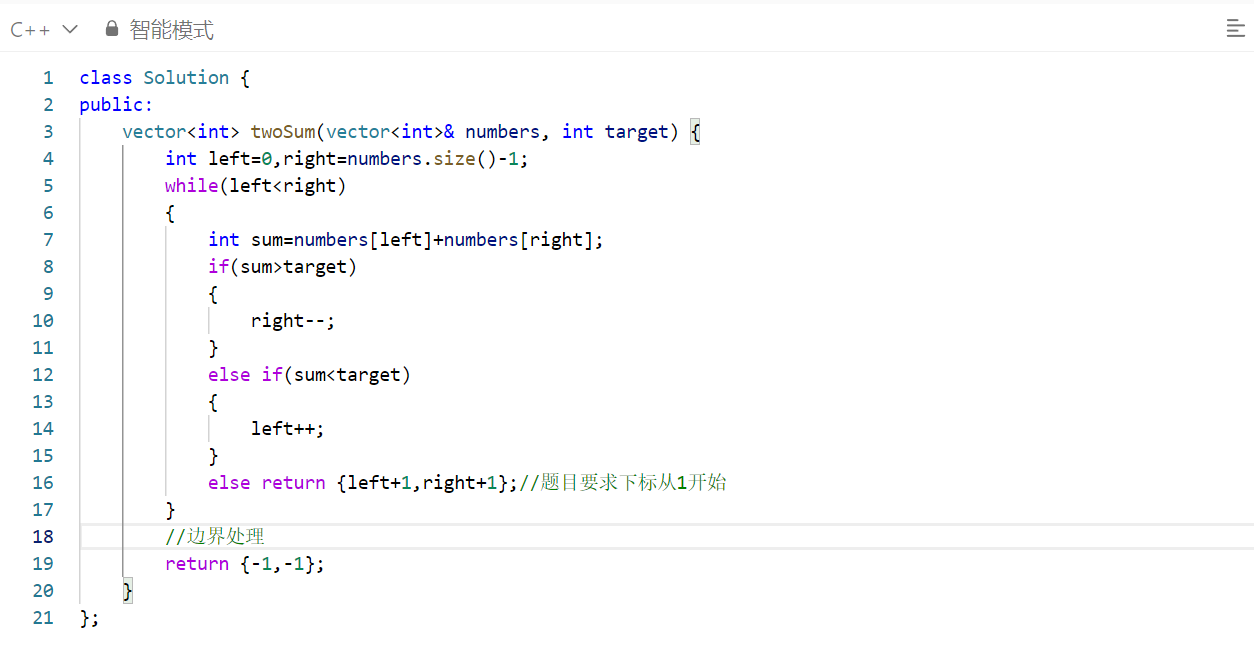
復雜度分析
1. 時間復雜度：O (n)
- 分析：算法使用雙指針（
left?和?right）從數組兩端向中間移動，每次循環僅移動一個指針，直到兩指針相遇（left >= right）。 - 最壞情況：兩個指針總共移動的次數不會超過數組長度?
n（例如，目標值需要最小元素和最大元素相加時，指針從兩端移動到相遇，總步數為?n?級）。 - 結論：時間復雜度為?O(n)，其中?
n?是數組?numbers?的長度。
2. 空間復雜度：O (1)
- 分析：算法僅使用了常數個額外變量（
left、right、sum），沒有使用與輸入規模相關的額外空間（如哈希表、數組等）。 - 結論：空間復雜度為?O(1)，屬于原地（in-place）算法。
如果是無序的，這里我們可以使用哈希表來解決！
哈希表法（無序）
解法思路：哈希表（空間換時間）
這個解法的核心是利用?哈希表（unordered_map）?存儲已經遍歷過的元素及其下標，通過一次遍歷就能找到答案，避免了暴力解法的二次循環。
具體邏輯：
- 遍歷數組中的每個元素?
nums[j]（j?是當前下標） - 計算與當前元素互補的數值：
complement = target - nums[j] - 檢查哈希表中是否存在?
complement：
- 若存在，說明之前已經遍歷過值為?
complement?的元素（下標為?i），則?i?和?j?就是答案 - 若不存在，將當前元素?
nums[j]?和其下標?j?存入哈希表，繼續遍歷
代碼執行流程（分步演示）
-
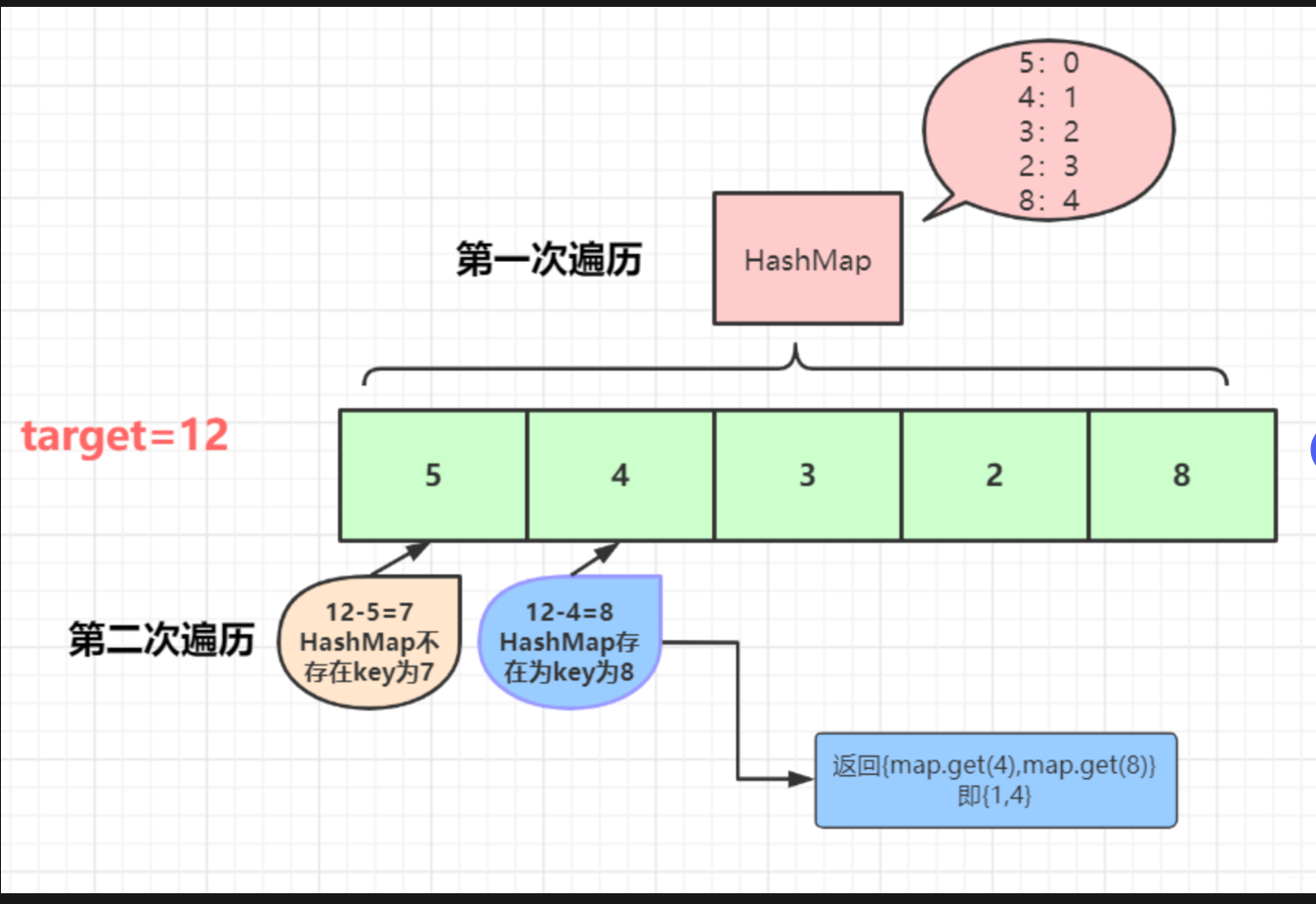
我們以?
nums = [5, 4, 3, 2, 8]?且?target = 12?為例，詳細演示代碼的執行過程。預期結果
在這個例子中，數組中?4 + 8 = 12，對應的下標是?
1?和?4，因此最終應該返回?[1, 4]。代碼執行步驟拆解
我們按照代碼的執行順序，一步步分析哈希表的變化和每輪循環的操作：
-
初始化：
- 創建空哈希表?
idx = {}（用于存儲已遍歷元素的值和下標） - 循環變量?
j?從?0?開始
- 創建空哈希表?
-
第一輪循環（j=0，當前元素 nums [0]=5）：
- 計算互補值：
complement = target - nums[j] = 12 - 5 = 7 - 檢查哈希表?
idx?中是否存在?7：此時哈希表為空，未找到 - 將當前元素存入哈希表：
idx[5] = 0（現在哈希表為?{5:0}） - 繼續下一輪循環
- 計算互補值：
-
第二輪循環（j=1，當前元素 nums [1]=4）：
- 計算互補值：
complement = 12 - 4 = 8 - 檢查哈希表?
idx?中是否存在?8：當前哈希表只有?5，未找到 - 將當前元素存入哈希表：
idx[4] = 1（現在哈希表為?{5:0, 4:1}） - 繼續下一輪循環
- 計算互補值：
-
第三輪循環（j=2，當前元素 nums [2]=3）：
- 計算互補值：
complement = 12 - 3 = 9 - 檢查哈希表?
idx?中是否存在?9：哈希表中只有?5?和?4，未找到 - 將當前元素存入哈希表：
idx[3] = 2（現在哈希表為?{5:0, 4:1, 3:2}） - 繼續下一輪循環
- 計算互補值：
-
第四輪循環（j=3，當前元素 nums [3]=2）：
- 計算互補值：
complement = 12 - 2 = 10 - 檢查哈希表?
idx?中是否存在?10：哈希表中沒有?10，未找到 - 將當前元素存入哈希表：
idx[2] = 3（現在哈希表為?{5:0, 4:1, 3:2, 2:3}） - 繼續下一輪循環
- 計算互補值：
-
第五輪循環（j=4，當前元素 nums [4]=8）：
- 計算互補值：
complement = 12 - 8 = 4 - 檢查哈希表?
idx?中是否存在?4：此時哈希表中存在?4，對應的下標是?1（即?idx[4] = 1） - 找到答案，直接返回?
[1, 4]（互補元素的下標?1?和當前元素的下標?4） - 程序結束
- 計算互補值：
-
代碼細節解析
完整代碼
-
哈希表的作用：
unordered_map<int, int> idx?中，key 是數組元素的值，value 是該元素的下標- 哈希表的查找操作是?O(1)?時間復雜度，比數組查找（O (n)）快得多
-
循環設計：
- 原代碼中的?
for (int j = 0; ; j++)?其實隱含了?j < nums.size()?的條件（題目保證有解，所以一定會在循環內返回） - 標準寫法應該是?
for (int j = 0; j < nums.size(); j++)，更嚴謹
- 原代碼中的?
-
避免重復使用元素：
- 因為我們是先檢查哈希表，再將當前元素存入哈希表，所以哈希表中永遠只包含「當前元素之前的元素」
- 這就保證了不會出現「自己和自己相加」的情況（例如?
nums = [3,3]?時，第一個 3 存入哈希表后，第二個 3 才會查找并命中）
-
返回值：
- 題目保證有且僅有一個解，所以循環內一定會找到答案并返回
- 理論上不需要最后的?
return {}，但為了滿足 C++ 語法（函數必須有返回值），通常會加上
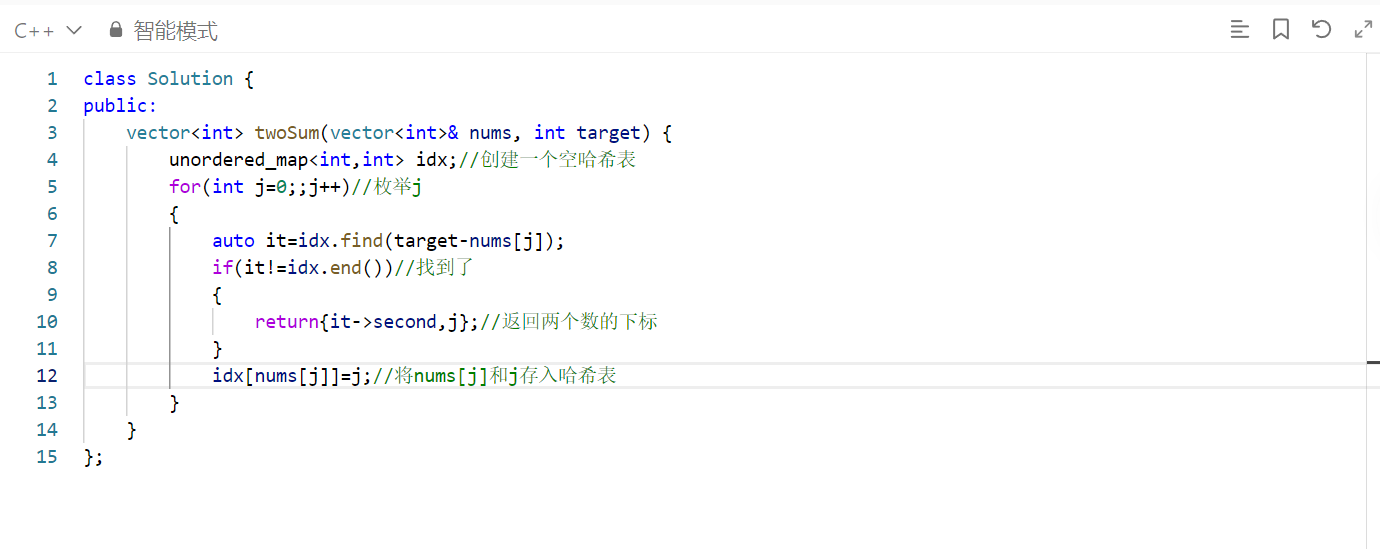
時間復雜度為 O(n)
)
 --運算符重載)
