還記得你第一次做出Meta分析時的成就感嗎？那種從海量文獻中抽絲剝繭，最終得出可靠結論的感覺，簡直不要太爽！
但是，時代在進步，科研在卷動，Meta分析也有它的"升級版"——傘狀Meta分析！
在醫學研究領域，每天都有海量新證據涌現。如何快速判斷某個結論是否可靠？當面對同一問題的數十篇Meta分析時，臨床醫生該信哪一篇？
答案或許藏在“傘狀Meta分析”中——它被譽為“證據金字塔尖的整合者”，能一鍵穿透爭議迷霧，告訴你真正的高質量結論。
??什么是傘狀Meta分析？
傘狀meta分析（Umbrella Review）是一種系統性評估方法，用于綜合評價某一領域內多個meta分析的結果。它通過整合多個相關meta分析的證據，提供更全面的結論，適用于復雜或存在爭議的研究領域。
? 為什么現在必須學傘狀Meta？
近年來，隨著學術研究的不斷深入和擴展，使用“umbrella review”、“systematic reviews of systematic reviews”、“umbrella systematic review”等關鍵詞在Web of Science數據庫中的檢索結果顯示，傘形綜述（umbrella reviews）相關文獻的發表數量呈現出顯著的逐年增長趨勢（如圖所示）。這一趨勢充分反映了該領域研究的蓬勃發展，并表明傘形綜述正日益受到學術界的廣泛關注和重視。
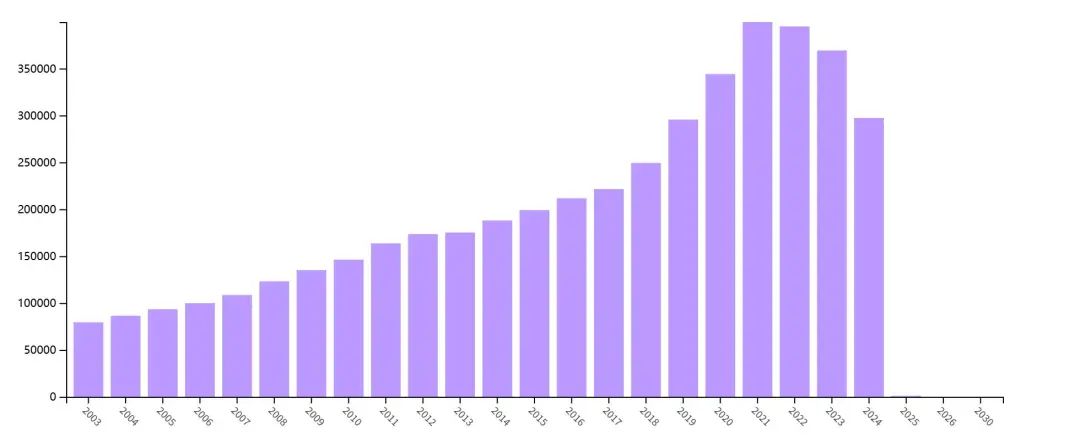?? 為什么現在必須學傘狀Meta？
🔥 證據更強：相比傳統Meta分析，結論更可靠
🔥 省時省力：1篇傘狀Meta ≈ 多篇傳統Meta
🔥 創新性強：國際頂刊趨勢，發文潛力巨大
🔥 工具成熟：首套完整方法論+實操工具包
今天，小優以下面這篇文獻跟大家分享一下此類課題的技術路線。
題目：癌癥患者疼痛、抑郁及焦慮的全球患病率與決定因素：系統評價和Meta分析的傘狀綜述
雜志：BMC Psychiatry
影響因子：IF=3.4
中科院分區：醫學二區
發表時間：2025年2月
Part 1：研究背景
抑郁、焦慮和痛苦是相互關聯的心理和身體狀況，它們共同影響個人的整體健康狀況。這些疾病會形成一個惡性循環，其中每個疾病都會放大另一個，導致生活質量的嚴重下降。對于癌癥幸存者來說，他們診斷和治療的情緒環與持續的心理壓力相聯系，會加劇身體痛苦，使人難以管理精神和身體癥狀。基于此，本研究通過傘狀綜述方法，系統評估全球范圍內癌癥患者疼痛、抑郁及焦慮癥狀的流行病學特征，并整合其關鍵生物-心理-社會決定因素。
Part 2：方法學
文獻檢索
本研究檢索于2024年7月1日至15日進行，涵蓋以下數據庫：MEDLINE、EMBASE、CINAHL、PubMed、ScienceDirect、Web of Science、Cochrane系統評價數據庫及PROSPERO（國際前瞻性系統評價注冊庫）。
結局變量的測量
本傘狀綜述聚焦三大核心結局指標：疼痛、抑郁與焦慮。疼痛評估采用多維測量工具組合策略，包括：
視覺模擬評分法（VAS）
數字評分法（NRS）
語言評分法（VRS）
二分類疼痛判定法（是/否）
針對采用VAS/NRS報告的疼痛程度數據，本研究引入Serlin分級標準進行疼痛強度分層（如：輕度≤3分，中度4-6分，重度≥7分）。在心理癥狀評估方面，采用醫院焦慮抑郁量表（HADS）與患者健康問卷（PHQ）雙量表驗證模式，確保癌癥患者焦慮抑郁狀態的精準識別。此外，本綜述通過跨文化視角系統解析全球范圍內癌癥患者焦慮與抑郁的生物-社會-臨床決定因素譜系。
偏倚風險評估
本研究采用系統評價方法學質量評估工具（AMSTAR）對納入的每項系統評價與Meta分析（SRMA）進行雙重質量核查，確保其方法學嚴謹性與證據可靠性。
Part 3：分析結果
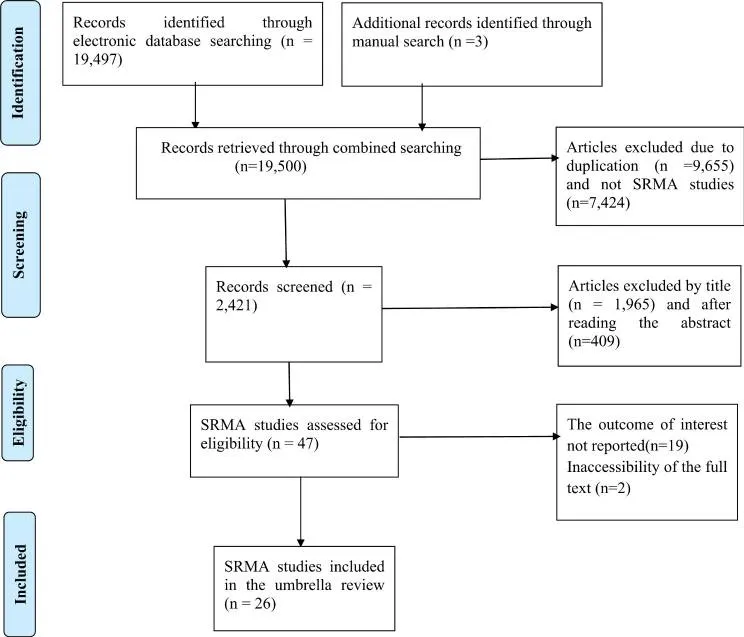
文獻檢索結果
最終，本傘狀綜述納入26項系統評價與Meta分析（SRMA）研究。
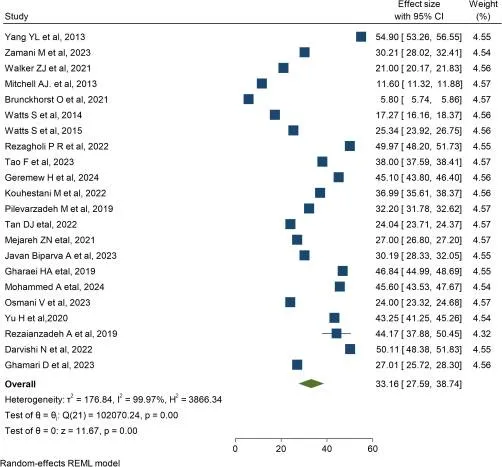
抑郁癥的患病率
全球癌癥幸存者抑郁癥狀匯總患病率為33.16%（95% CI 27.59–38.74）。異質性分析顯示I2指數達99.7%（p<0.001），提示極高異質性。漏斗圖不對稱分布提示潛在發表偏倚，Egger檢驗（p=0.001）證實此偏倚，表明陰性/中性結果的小型研究可能未被充分發表。通過Trim and Fill分析填補12項潛在缺失研究后，校正后抑郁患病率降至12.03%（95% CI 6.41–17.65），較原始值下降63.7%，提示未發表研究可能顯著影響原始結果的高估。
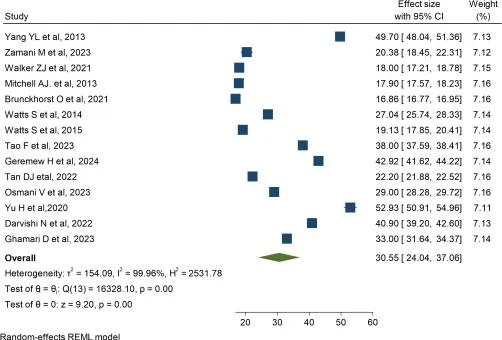
焦慮癥的患病率
全球癌癥幸存者焦慮癥狀匯總患病率為30.55%（95% CI 24.04–37.06）。異質性分析顯示I2指數高達99.96%（p<0.001），提示研究間存在極端異質性。Egger檢驗（p<0.001）與漏斗圖不對稱性證實存在顯著發表偏倚，暗示小樣本或陰性結果研究可能未被充分發表。通過Trim and Fill分析填補8項潛在缺失研究后，焦慮患病率修正為17.80%（95% CI 13.18–22.41），較原始值下降41.7%，表明未發表研究導致原始結果系統性高估。
疼痛的發生率
本傘狀綜述系統解析了全球癌癥幸存者的疼痛患病率，涵蓋治療前、治療期間及治療后的疼痛動態演變。數據顯示：
治療前：近2/3患者（65.22%，95% CI 62.86–67.57）存在疼痛癥狀。
治療期間：51.34%（95% CI 40.01–62.67）患者仍受疼痛困擾。
治療后：39.77%（95% CI 31.84–47.70）幸存者存在持續性疼痛。
整體趨勢表明，癌癥治療可降低疼痛發生率，但近四成幸存者在治療結束后仍受疼痛影響，提示現行疼痛管理策略存在"療效衰減窗口"。
Part 4：討論
本傘狀綜述揭示癌癥幸存者心理健康與疼痛負擔嚴峻：抑郁、焦慮及治療后疼痛的全球患病率分別為33.16%、30.55%和39.77%，其中治療前疼痛率高達65.22%。核心風險因素包括疾病復發恐懼、治療副作用及社會支持缺失，同時存在顯著地域與人群差異（如亞洲患者心理癥狀報告率低于歐美）。研究強調需構建整合心理干預-疼痛管理-長期監測的跨學科照護體系，并為優化臨床指南（如制定分階段疼痛控制路徑）及公共衛生政策（如增加心理健康服務資源配置）提供循證依據。
Part 5：小優結語
傘狀Meta分析揭示癌癥幸存者真實負擔：比如校正偏倚后抑郁率驟降（33%→12%），凸顯其整合證據、識別偏倚的核心價值。它不僅是數據校正器，更是臨床決策的指南針——指導精準干預，重塑從“生存”到“生活”的癌癥康復體系。
為什么傘狀meta被稱為“證據天花板”？
??廣度MAX：橫跨所有相關Meta分析，避免“只見樹木不見森林”
??權威性MAX：僅納入高質量研究，用AMSTAR等工具嚴篩證據
??結論可視化：通過分級系統（如GRADE）標記證據等級，紅黃綠燈一目了然
（舉個栗子🌰）
某疾病有20篇Meta分析探討維生素D的療效，結論卻互相矛盾。傘狀分析可統一評估：
哪些劑量真正有效？（如2000IU/天改善骨密度：證據A級）
哪些聲稱的“副作用”其實證據薄弱？（如“導致腎損傷”：證據D級）
哪些場景必須用它？
🔍?臨床決策糾結時：當指南推薦存在沖突
🔍?科研選題迷茫時：快速定位領域內最強證據缺口
🔍?政策制定爭議時：用全景證據支持資源分配
經典案例：
《英國醫學雜志》（BMJ）曾用傘狀分析揭秘“營養神藥”真相——綜合530篇Meta分析后發現，80%的膳食補充劑對健康人無益， Omega-3、維生素D等僅對特定人群有效。
未來已來，你準備好“撐傘”了嗎？
在循證醫學的暴雨中，傘狀Meta分析正成為臨床、科研、政策領域的**“決策導航儀”。
)
