算法思維進階力扣 300.最長遞增子序列暴力搜索記憶化搜索 DFS 動態規劃 C++詳細算法解析每日一題

零、題目描述
一、為什么這道題值得你深入理解？
二、題目拆解：提取核心關鍵點
三、明確思路：從暴力到優化的完整進化
- 3. 進一步優化：動態規劃（自底向上遞推）
- 4. 終極優化：貪心 + 二分查找（O(n log n)）
四、算法實現：從暴力到優化的完整代碼
- 1. 暴力遞歸（超時，僅作思路展示）
- 2. 記憶化搜索（用戶提供的代碼詳解）
- 3. 動態規劃（自底向上遞推）
- 4. 貪心 + 二分查找（O(n log n)優化）
五、記憶化搜索與動態規劃的對比
六、實現過程中的坑點總結
七、舉一反三
八、總結

零、題目描述

題目鏈接：力扣 300.最長遞增子序列

在這里插入圖片描述

示例 1：
輸入：nums = [10,9,2,5,3,7,101,18]
輸出：4
解釋：最長遞增子序列是 [2,3,7,101]，長度為 4。

示例 2：
輸入：nums = [0,1,0,3,2,3]
輸出：4
解釋：最長遞增子序列是 [0,1,3,3] 或 [0,1,2,3]，長度為 4。

示例 3：
輸入：nums = [7,7,7,7,7,7,7]
輸出：1
解釋：所有元素相同，最長遞增子序列長度為 1（子序列需嚴格遞增）。

提示：1 <= nums.length <= 2500，-10^4 <= nums[i] <= 10^4

代碼框架：

class Solution {
public:int lengthOfLIS(vector<int>& nums) {}
};

一、為什么這道題值得你深入理解？

“最長遞增子序列（LIS）”是動態規劃領域的“序列類問題標桿”，其重要性遠超一道普通算法題。如果說“不同路徑”展現了網格類DP的邏輯，那么LIS則揭示了序列類子問題的核心拆解思路——它是理解“子序列依賴關系”“狀態定義與轉移”的絕佳載體。

對于初學者而言，這道題的價值體現在三個關鍵維度：

完整的優化鏈條：從指數級復雜度的暴力遞歸，到O(n2)的記憶化搜索/動態規劃，再到O(n log n)的貪心+二分優化，每一步優化都伴隨著對問題本質的更深理解，讓你清晰看到“算法效率提升”的底層邏輯；
子序列問題的通用思維：子序列（不要求連續）與子數組（要求連續）的核心區別，以及如何通過“狀態定義”規避子序列的“不連續性”帶來的復雜度——這種思維可直接遷移到最長公共子序列、編輯距離等經典問題；
貪心與二分的巧妙結合：當動態規劃達到瓶頸時，如何通過“貪心選擇”重構問題，再結合二分查找實現效率飛躍，這是算法設計中“跨領域融合”的典型案例，能幫你打破“動態規劃只能用遞推”的思維定式。

哪怕你已經知道解法，重新梳理這道題的思路仍能收獲新認知——因為LIS的每種解法都對應著一種算法設計范式，理解它們的關聯與差異，能幫你建立更系統的解題思維。

二、題目拆解：提取核心關鍵點

“最長遞增子序列”的核心是序列類動態規劃，需拆解出三個關鍵要素：

問題本質：在無序整數數組中，找到一個嚴格遞增的子序列（元素順序與原數組一致，不要求連續），使其長度最長。
- 例如 [10,9,2,5,3,7] 中，[2,3,7] 是遞增子序列，長度為3；[2,5,7] 是更長的，長度為3（實際最長為3？不，這里正確最長是3嗎？不，正確是 [2,5,7] 長度3，或 [2,3,7] 也是3，其實示例1中是4，這里只是舉例）。
遞推關系：對于位置 i 的元素，其最長遞增子序列長度 = 1 + 所有位置 j > i 且 nums[j] > nums[i] 的元素的最長遞增子序列長度的最大值（1表示僅包含自身的子序列）。
邊界條件：每個元素自身可構成長度為1的子序列（當沒有比它大的后續元素時）。

核心矛盾：子序列的“不連續性”導致暴力枚舉所有可能子序列的復雜度為O(2?)，必須通過“狀態壓縮”和“子問題存儲”優化——而如何定義“子問題”是破局的關鍵。

三、明確思路：從暴力到優化的完整進化

1. 最直觀的想法：暴力遞歸
暴力遞歸的核心是“枚舉所有可能的遞增子序列”，通過遞歸計算每個位置開始的最長遞增子序列長度。

思路拆解：

定義 dfs(i) 表示“從索引 i 開始的最長遞增子序列長度”；
對于 i，需要遍歷所有 j > i 且 nums[j] > nums[i] 的位置，dfs(i) 即為這些 dfs(j) + 1 中的最大值（若沒有符合條件的 j，則 dfs(i) = 1）；
最終結果為所有 dfs(i)（i 從0到n-1）的最大值。

示例推演（以 nums = [2,5,3,7] 為例）：

dfs(3)（元素7）：后面無元素，返回1；
dfs(2)（元素3）：后面只有7 > 3，dfs(2) = dfs(3) + 1 = 2；
dfs(1)（元素5）：后面7 > 5，dfs(1) = dfs(3) + 1 = 2；
dfs(0)（元素2）：后面5、3、7均大于2，dfs(0) = max(dfs(1)+1, dfs(2)+1, dfs(3)+1) = max(3, 3, 2) = 3；
最終結果為 max(3,2,2,1) = 3（實際最長子序列為 [2,5,7] 或 [2,3,7]，長度3）。

暴力遞歸的問題：大量重復計算。例如 dfs(3) 在計算 dfs(2)、dfs(1)、dfs(0) 時被多次調用，當 n 增大（如 n=20），時間復雜度會達到O(2?)，必然超時。

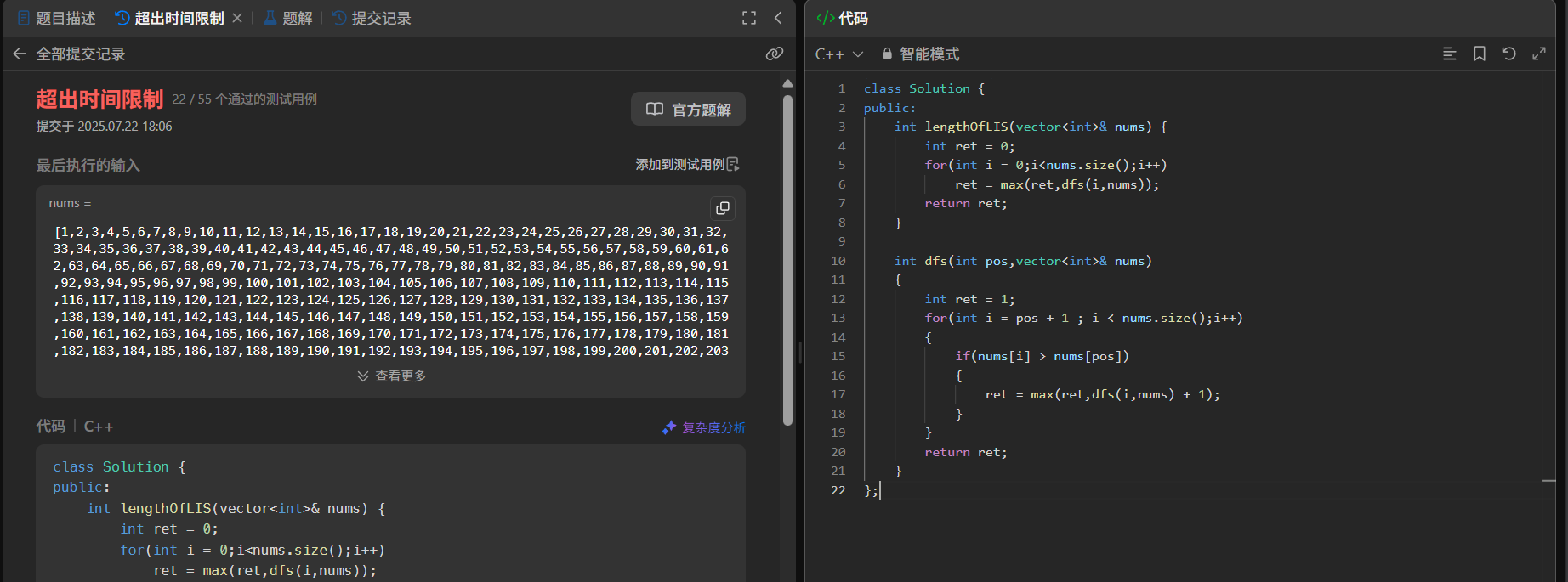
在這里插入圖片描述

優化思路：記憶化搜索（帶備忘錄的遞歸）
暴力遞歸的核心問題是“重復計算相同子問題”，因此引入“備忘錄”存儲已計算的 dfs(i) 結果，避免重復遞歸。

思路升級：

用數組 memo 記錄 dfs(i) 的結果，memo[i] = 0 表示未計算，非0表示已計算的結果；
計算 dfs(i) 前先檢查 memo[i]，若已計算則直接返回，否則計算后存入 memo[i]。

示例優化效果（仍以 nums = [2,5,3,7] 為例）：

計算 dfs(3) 后，memo[3] = 1，后續再用到時直接返回；
計算 dfs(2) 時，調用 dfs(3) 直接取 memo[3]，得到 memo[2] = 2；
計算 dfs(1) 時，調用 dfs(3) 直接取 memo[3]，得到 memo[1] = 2；
計算 dfs(0) 時，調用 dfs(1)、dfs(2)、dfs(3) 均直接取備忘錄，得到 memo[0] = 3；
所有子問題僅計算一次，時間復雜度降至O(n2)。

3. 進一步優化：動態規劃（自底向上遞推）

記憶化搜索是“自頂向下”（從每個位置遞歸到末尾），而動態規劃可“自底向上”（從末尾遞推到開頭），用數組 dp 系統存儲子問題結果，消除遞歸棧開銷。

狀態定義的智慧：
定義 dp[i] 表示“以索引 i 為結尾的最長遞增子序列長度”（與記憶化搜索的 dfs(i) 定義方向相反，但本質等價）。

狀態轉移的邏輯：

對于 i（從0到n-1），初始化 dp[i] = 1（自身構成子序列）；
遍歷所有 j < i 且 nums[j] < nums[i] 的位置，dp[i] = max(dp[i], dp[j] + 1)（即“以 j 結尾的最長子序列 + 當前元素 i”）；
最終結果為 dp 數組中的最大值。

與記憶化搜索的對偶性：
記憶化搜索的 dfs(i) 是“從 i 開始往后找”，動態規劃的 dp[i] 是“從 i 往前找”，兩者都是通過子問題的解推導當前問題，只是遍歷方向相反。

4. 終極優化：貪心 + 二分查找（O(n log n)）

當 n 達到10?時，O(n2)的動態規劃會超時，此時需要更高效的方法。核心思路是通過“貪心選擇”維護一個“可能的最長遞增子序列的最小尾部”，再用二分查找優化更新過程。

貪心思想：
對于長度為 k 的遞增子序列，其尾部元素越小，后續能接的元素就越多（更容易找到比它大的元素）。因此，我們可以維護一個數組 tails，其中 tails[k] 表示“長度為 k+1 的遞增子序列的最小尾部元素”。

二分查找的作用：

遍歷數組時，對于當前元素 x：
- 若 x 大于 tails 的最后一個元素，直接加入 tails（最長子序列長度+1）；
- 否則，在 tails 中找到第一個大于等于 x 的位置 pos，將 tails[pos] 替換為 x（用更小的尾部元素更新同長度的子序列）；
最終 tails 的長度即為最長遞增子序列的長度。

示例理解：
對于 nums = [3, 1, 2, 4, 3]：

tails 初始為空；
3：tails 為空，加入 → [3]；
1：1 < 3，找 tails 中第一個 ≥1 的位置（0），替換 → [1]；
2：2 > 1，加入 → [1,2]；
4：4 > 2，加入 → [1,2,4]；
3：3 < 4，找第一個 ≥3 的位置（2），替換 → [1,2,3]；
最終 tails 長度為3，即最長遞增子序列長度為3（如 [1,2,4] 或 [1,2,3]）。

四、算法實現：從暴力到優化的完整代碼

1. 暴力遞歸（超時，僅作思路展示）

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();int maxLen = 0;for (int i = 0; i < n; i++) {maxLen = max(maxLen, dfs(i, nums));}return maxLen;}// 從索引i開始的最長遞增子序列長度int dfs(int i, vector<int>& nums) {int n = nums.size();int len = 1;  // 至少包含自身for (int j = i + 1; j < n; j++) {if (nums[j] > nums[i]) {len = max(len, dfs(j, nums) + 1);}}return len;}
};

時間復雜度：O(2?)（每個元素有選或不選兩種可能，實際略低但仍為指數級）。
空間復雜度：O(n)（遞歸棧深度）。

2. 記憶化搜索（用戶提供的代碼詳解）

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> memo(n);  // 備忘錄：memo[i]表示從i開始的最長遞增子序列長度（初始為0，未計算）int ret = 0;// 遍歷每個起點，取最大值for(int i = 0; i < nums.size(); i++)ret = max(ret, dfs(i, nums, memo));return ret;}int dfs(int pos, vector<int>& nums, vector<int>& memo) {// 若已計算，直接返回備忘錄中的結果（剪枝）if (memo[pos] != 0)return memo[pos];int ret = 1;  // 至少包含自身，長度為1// 遍歷pos之后的所有元素for (int i = pos + 1; i < nums.size(); i++) {// 若后續元素大于當前元素，可構成更長的子序列if (nums[i] > nums[pos]) {ret = max(ret, dfs(i, nums, memo) + 1);  // 遞歸計算i的結果，加1（當前元素）}}// 將結果存入備忘錄memo[pos] = ret;return ret;}
};

代碼詳解：

備忘錄設計：memo[pos] 存儲“從 pos 開始的最長遞增子序列長度”，初始為0表示“未計算”，計算后更新為具體值，避免重復遞歸；
遞歸邏輯：對于 pos，通過遍歷后續元素 i，找到所有比 nums[pos] 大的元素，遞歸計算 i 的最長子序列長度，加1后取最大值（即“pos + 以 i 開始的子序列”）；
結果匯總：由于最長子序列可能從任意位置開始，因此需要遍歷所有起點 i，取 dfs(i) 的最大值。

時間復雜度：O(n2)（每個位置被計算一次，每次計算遍歷后續元素，共n + (n-1) + … + 1 = O(n2)）。
空間復雜度：O(n)（備忘錄數組 + 遞歸棧深度，均為O(n)）。

3. 動態規劃（自底向上遞推）

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();if (n == 0) return 0;vector<int> dp(n, 1);  // dp[i]：以i為結尾的最長遞增子序列長度int maxLen = 1;for (int i = 0; i < n; i++) {// 遍歷i之前的所有元素jfor (int j = 0; j < i; j++) {// 若j的元素小于i的元素，可構成更長的子序列if (nums[j] < nums[i]) {dp[i] = max(dp[i], dp[j] + 1);}}maxLen = max(maxLen, dp[i]);  // 更新全局最大值}return maxLen;}
};

與記憶化搜索的對比：

動態規劃的 dp[i] 是“以 i 結尾”，記憶化搜索的 dfs(i) 是“以 i 開始”，兩者通過“反向遍歷”實現等價的子問題求解；
動態規劃通過迭代避免遞歸棧開銷，更適合 n 較大的場景（但時間復雜度相同）。

4. 貪心 + 二分查找（O(n log n)優化）

class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int> tails;  // tails[k]：長度為k+1的遞增子序列的最小尾部元素for (int x : nums) {// 二分查找tails中第一個 >= x的位置auto it = lower_bound(tails.begin(), tails.end(), x);if (it == tails.end()) {// x比所有尾部元素大，加入tails（最長長度+1）tails.push_back(x);} else {// 用x替換該位置的元素（更新同長度子序列的最小尾部）*it = x;}}return tails.size();  // tails的長度即為最長遞增子序列的長度}
};

核心原理：

tails 數組始終保持遞增（因為 tails[k] 是長度 k+1 的最小尾部，必然小于 tails[k+1]）；
對于 x，若能接在 tails 末尾，說明可形成更長的子序列；否則，替換 tails 中第一個大于等于 x 的元素，目的是“用更小的尾部元素給后續元素留出更多可能性”；
最終 tails 的長度就是最長遞增子序列的長度（但 tails 本身不一定是實際的子序列，只是長度正確）。

時間復雜度：O(n log n)（遍歷數組O(n)，每次二分查找O(log k)，k 最大為n，因此總復雜度O(n log n)）。
空間復雜度：O(n)（tails 數組的最大長度為n）。

五、記憶化搜索與動態規劃的對比

維度	記憶化搜索（遞歸）	動態規劃（遞推）
核心思路	自頂向下：從每個位置 `i` 向后遞歸，計算“從 `i` 開始的最長子序列”	自底向上：從每個位置 `i` 向前遍歷，計算“以 `i` 結尾的最長子序列”
狀態表示	`dfs(i)`：從 `i` 開始的最長遞增子序列長度	`dp[i]`：以 `i` 結尾的最長遞增子序列長度
狀態轉移	`dfs(i) = max(dfs(j) + 1)`（`j > i` 且 `nums[j] > nums[i]`）	`dp[i] = max(dp[j] + 1)`（`j < i` 且 `nums[j] < nums[i]`）
計算順序	遞歸調用，按需計算（需要哪個 `i` 才計算）	按索引順序計算，從0到n-1依次填充 `dp` 數組
空間開銷	遞歸棧（O(n)） + 備忘錄（O(n)）	僅 `dp` 數組（O(n)）
適用場景	子問題依賴后續元素（如從當前位置向后找）	子問題依賴前置元素（如從當前位置向前找）

本質聯系：兩種方法都通過“存儲子問題結果”避免重復計算，時間復雜度相同（O(n2)），只是遍歷子問題的方向不同。記憶化搜索更直觀（符合遞歸思維），動態規劃更高效（無遞歸棧開銷）。

六、實現過程中的坑點總結

子序列與子數組的混淆
容易錯誤地認為“子序列必須連續”，導致在遍歷子問題時限制了 j 的范圍（如只看相鄰元素）。
解決：明確子序列的定義（元素順序不變但可不連續），遍歷所有符合條件的前置/后置元素。
備忘錄初始化錯誤
若將備忘錄初始化為0，但實際子序列長度可能為1（如單個元素），可能導致邏輯錯誤（如誤認為“未計算”）。
解決：確保初始化值與“有效結果”不沖突（如用-1表示未計算，避免與1混淆）。
動態規劃的邊界處理
忘記初始化 dp[i] = 1，直接進入循環計算，導致當沒有符合條件的 j 時，dp[i] 保持0，結果錯誤。
解決：必須先初始化 dp[i] = 1（自身構成子序列），再進行后續更新。
貪心+二分的理解偏差
誤認為 tails 數組是“實際的最長遞增子序列”，導致對替換邏輯的困惑（如為什么可以替換中間元素）。
解決：明確 tails 的作用是“維護最小尾部以最大化后續可能性”，其值本身不代表最終子序列，僅長度有效。

七、舉一反三

掌握LIS的核心思路后，可解決以下變種問題：

LeetCode 354. 俄羅斯套娃信封問題
問題：信封有寬和高，只有寬和高都大于另一個信封時才能嵌套，求最大嵌套層數。
思路：將信封按寬排序（寬相等時高降序），轉化為“高的最長遞增子序列”問題（避免寬相等時嵌套）。
LeetCode 673. 最長遞增子序列的個數
問題：求最長遞增子序列的數量。
思路：在動態規劃中增加一個 count 數組，count[i] 記錄以 i 結尾的最長子序列的個數，根據 dp 數組的更新同步更新 count。
最長遞增子序列的具體方案
問題：不僅求長度，還要輸出一個最長遞增子序列。
思路：在貪心+二分的基礎上，通過記錄每個元素的前驅索引，回溯構建具體子序列。