河南萌新聯賽2025第（二）場：河南農業大學

我看到花兒在綻放我聽到鳥兒在歌唱我看到人們匆匆忙忙
我看到云朵在天上我聽到小河在流淌我看到人們漫步在路上

河南萌新聯賽2025第（二）場：河南農業大學

河南萌新聯賽2025第（二）場：河南農業大學_ACM/NOI/CSP/CCPC/ICPC算法編程高難度練習賽_牛客競賽OJ

第二場，暴露了很多問題，這次的題目數學數論題居多，有點樣例都看不明白，做的時候都快崩潰了。~~數學不好太難了~~；數論還沒咋看，導致一些簡單的題推不出來；有一些模板題沒見過很不好想，但是想明白后不算難；

預估難度：

簡單：K I M D
中等：E C B A L
較難：H G
困難：J F

我的做題順序 K I M D A，數學太難了_XD；雖然最后榜又歪了但是這次影響不大，自己做題的順序也是按難度來的；

河南萌新聯賽2025第（二）場：河南農業大學
- K-打瓦
- I-猜數游戲(easy)
- M-米婭逃離斷頭臺
- D-開羅爾網絡的備用連接方案
- E-咕咕嘎嘎!!!(easy)
- C-O神
- B-異或期望的秘密
- - 小藍的二進制詢問
  - 累加器
  - 異或期望的秘密
- A-約數個數和
- - 整除分塊

K-打瓦

簽到題，使出PHP大法；

gugugaga

PHP 是一種創建動態交互性站點的強有力的服務器端腳本語言。意思就是說php語言會把不是代碼的東西直接輸出；

I-猜數游戲(easy)

簽到題；最優策略肯定是二分的思路去猜，所以需要log2(n)次，向上取整；

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define pii pair<int,int>
#define fi first
#define se second
const int inf=0x3f3f3f3f;
const int N=1e5+5;
void slove(){int n;cin>>n;int an=(int)log2(n);if(log2(n)>an) an++;cout<<an;
} 
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;//cin>>_;while(_--)slove();return 0;
}

M-米婭逃離斷頭臺

數學題；設大圓半徑為 $a$ 小圓半徑為 $b$ 從圓心連向切線要求的面積為 $π×(a2?b2)/2\pi\times(a^2-b^2)/2$ ,又勾股定理可得 $a^2-b^2=x^2/4$ ，固答案為 $π×x2/8\pi\times x^2/8$ 。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define pii pair<int,int>
#define fi first
#define se second
const int inf=0x3f3f3f3f;
const int N=1e5+5;
const double pi=3.1415926535;
void slove(){int x;cin>>x;double c=x/2.0;double an=0.5*pi*c*c;printf("%.2lf",an);
} 
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;//cin>>_;while(_--)slove();return 0;
}

D-開羅爾網絡的備用連接方案

一道很簡單的遍歷樹的題，先按要求建樹，然后dfs遍歷統計到達每個節點是當前值的二進制數里一的個數，最后多次尋問含有相應個數的1的節點有幾個，對應查詢就好；

輸入邊的時候順序不是固定的，所以建樹的時候記得建雙向邊！這樣才能把圖連起來；便利的時候打標記或記錄父節點，防止走回頭路；

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define pii pair<int,int>
#define fi first
#define se second
const int inf=0x3f3f3f3f;
const int N=1e5+5;
vector<int> e[N];
int a[N];
int an[N];
void dfs(int x, int w, int f){  int c = a[x]&w;bitset<35> b(c);an[b.count()]++;for (int i : e[x]) {if (i==f) continue; dfs(i,c,x); }
}
void slove() {int n, q;cin >> n >> q;for (int i = 1; i <= n; i++) cin >> a[i];for (int i = 1; i < n; i++) {int u, v;cin >> u >> v;e[u].push_back(v);e[v].push_back(u); }dfs(1,-1,0);while (q--) {int x;cin >> x;cout << an[x] << endl;}
}
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;//cin>>_;while(_--)slove();return 0;
}

這題的題目描述真是一言難盡，連最基本的需求都表達不清楚；第一次用比賽的小喇叭，沒想到出題人還真的回復了；后面補充過后明白題意后操作起來就很簡單；

E-咕咕嘎嘎!!!(easy)

數據很小，而且輸入的是一個數，一開始想的是dfs枚舉，但估計會超時，于是就想動態規劃或者數學推導；但是太菜了沒推出來；

題解中給出的動態規劃的寫法，有點類似于暴力，三重循環，i表示枚舉新選進去的數，j枚舉選了這個數后所有gcd的情況，k表示已經選取的序列的長度有點類似01背包，看看是加上這一位更優還是不加更優，這題里面不牽扯物品的價值價值，所以直接加也可以；

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define pii pair<int,int>
#define fi first
#define se second
const int inf=0x3f3f3f3f;
const int N=5e3+5;
const int M=1e9+7;
int dp[N][N];
void slove(){int n,m;cin>>n>>m;for(int i=2;i<=n;i++)dp[i][1]=1;for(int i=2;i<=n;i++){ // 枚舉的是選進去的數for(int j=2;j<i;j++){ // 枚舉的是前面狀態的gcd是多少for(int k=m;k>=2;k--){ // 枚舉級精選取得序列長度的長度,每一維都相當于是個01背包，所以倒序dp[__gcd(i,j)][k]=max(dp[__gcd(i,j)][k],dp[__gcd(i,j)][k]+dp[j][k-1]);dp[__gcd(i,j)][k]%=M;}}}int an=0;for(int i=2;i<=n;i++)an+=dp[i][m],an%=M;cout<<an;
} 
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;//cin>>_;while(_--)slove();return 0;
}

C-O神

這題感覺還是比較有意思的，不太好想，被題目中設立的情境給迷惑了；比賽的時候以為就是一個大模擬，但是賽后看題解才看出來居然是個背包dp；使用 dp[j]表示消耗 j能獲得的最大收益。把最優的充值情況記錄下來；然后看每一抽在最優的情況下需要花費多少的錢記錄在新的數組b[]中；

但是這個樣例看著太奇怪了，比賽的時候根本沒看懂，正常的概率不應該是小數嗎？后面發現是乘法逆元的緣故：

在普通數學中，概率 $pq\frac pq$ 是一個小于等于1的分數。但在模數下，分數 $pq\frac pq$ 被表示為 $p×q?1p\times q^{-1}$ mod $M$ ,其中 $q^{-1}$ 是 $q$ 的模逆元。模逆元 $q^{-1}$ 通常是一個很大的數(因為 $q$ 是小整數時， $q^{-1}\mod M$ 接近 $M$ )。期望計算中，每一項 $b[i]×p×qkb[i]\times p\times q^k$ 在模數下會被放大 $\frac pq$ 在模數下是 $p×q?1modMp\times q^-1\mod M$ (大數)。 $q^k$ 是 $1-p)^k\mod M$ ,但通常仍是大數。最終累加時，這些大數相乘再取模，結果可能仍然很大。進一步了解好像是大二會學到的離散；

對概率逆元操作完之后，把每一抽的期望[總概率（成功的概率×當前失敗的概率）×代價]計算出來累加就好了！

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define pii pair<int,int>
#define fi first
#define se second
const int inf=0x3f3f3f3f;
const int N=2e3+3;
const int M=1e9+7;
int dp[N],b[N];
pii a[N];
int kksu(int a,int b){a%=M;int s=1;while(b){if(b&1){s*=a;s%=M;}a*=a;a%=M;b>>=1;}return s;
}
void slove(){int x,p,q,m;cin>>x>>p>>q>>m;int n;cin>>n;for(int i=1;i<=n;i++)cin>>a[i].fi>>a[i].se;for(int i=1;i<=n;i++)for(int j=N;j>=a[i].fi;j--)dp[j]=max(dp[j],dp[j-a[i].fi]+a[i].se);int t=0;for(int i=1;i<=m;i++){while(dp[t]<x*i)t++;b[i]=t;}int p1=p*kksu(q,M-2)%M;int q1=((1-p1)%M+M)%M;t=1;int an=0;for(int i=1;i<m;i++){an+=b[i]*p1%M*t%M;an%=M;t*=q1;t%=M;}an+=t*b[m];cout<<an%M;
} 
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;//cin>>_;while(_--)slove();return 0;
}

但是代碼里面的細節超級多，超級容易寫錯，因為逆元的緣故，所以基本上計算的地方都要一直去取模；

B-異或期望的秘密

這題沒看懂的原因和上一題一樣，不明白樣例里面為什么突然變得那么大，還是對乘法逆元的理解不夠深刻！

看懂后其實不難理解；

再具體的看這題之前先看下面這兩題；

小藍的二進制詢問

D-小藍的二進制詢問_河南萌新聯賽2024第（一）場：河南農業大學

~~不難發現，這道題也是這個人出的~~

題目要求計算區間 [l, r]內所有整數的二進制表示中1的個數之和的問題。核心策略是利用按位計算的方法高效地計算從0到任意整數n（包括n）的二進制1的個數之和，然后通過前綴和思想計算區間和。

整體的思想就是類似于前綴和的思想對于查詢 [l, r]，區間和等于 f(r) - f(l-1)，即：
$ans=(∑i=0rpopcount(i))?(∑i=0l?1popcount(i))\text{ans} = (\sum_{i=0}^{r} \text{popcount}(i)) - (\sum_{i=0}^{l-1} \text{popcount}(i))$

f(n)計算從0到n（包括0和n）的所有整數的二進制表示中1的個數之和。

循環條件：變量 t從2開始，每次左移一位(即t * =2),直到t>=n * 2。

周期貢獻：對于每個位位置 (相當于以 t為周期),完整周期的個數是n/t。每個周期中該位為1的個數是 t/2。因此，完整周期貢獻為：(n/t)*(t/2)。

以i=2，第二位為例

十進制數  二進制   第2位
0        000      0  ← 周期開始
1        001      0
2        010      0
3        011      0 
4        100      1
5        101      1
6        110      1
7        111      1
8       1000      0   ← 下一個周期開始
...

周期長度：T = 2ⁱ⁺¹ = 8
每個周期內：前2ⁱ個數第2位為0，后4個數為1

所以得到每一位的周期就是T = 2ⁱ⁺¹，周期內1的個數就是2ⁱ；

剩余部分貢獻：在一個不完整的周期中，如果余數n%t大于 t/2,則剩余部分中該位為1的個數是 n%t- t/2。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define pii pair<int,int>
#define fi first
#define se second
const int inf=0x3f3f3f3f;
const int N=1e5+5;
const int M=998244353;
int f(int n){if(n==0) return 0;int s=0,t=2;n++;while(t<n*2){s+=n/t*(t/2);if(n%t>t/2) s+=n%t-t/2;s%=M;t<<=1;}return s%M;
}
void slove(){int l,r;cin>>l>>r;cout<<(f(r)-f(l-1)+M)%M<<endl; 
} 
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;cin>>_;while(_--)slove();return 0;
}

累加器

F-累加器_河南萌新聯賽2024第（三）場：河南大學

這題要讓我們看從x到x＋y這期間，對應二進制的數的每一位；可以延續上一題的思路；我們看看從0到x+y中變了多少次再減去從0到x變了多少次，就是我們的結果；

這道題我們只用找到他變化的周期就行，不要再具體看有幾個1了，所以更簡單點；

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define pii pair<int,int>
#define fi first
#define se second
const int inf=0x3f3f3f3f;
const int N=1e5+5;
const int M=998244353;
int f(int x){int s=0;int t=1;while(t<=x){s+=x/t;t<<=1;}return s;
}
void slove(){int x,y;cin>>x>>y;cout<<f(x+y)-f(x)<<endl;
} 
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;cin>>_;while(_--)slove();return 0;
}

異或期望的秘密

現在我們再回來看這道題；這題看著帶這個異或的字樣，其實和異或關系并不大；異或時相同的位會被賦予0，所以我們去找不同的位的個數，再去比上區間長，就是我們所求的期望；

為了方便統計，我們就一位一位的看，看看這個區間的數的這一位上有幾個1幾個0，再看參與運算的k這一位是1還是0，找到不一樣的那個數的個數，累加的分子里面；最后計算出的結果是個分數，題目要求輸出逆元的形式；和上面的推導是一樣的；這里每次f函數判斷一位就行，遍歷每一位的for在主函數中；

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define pii pair<int,int>
#define fi first
#define se second
const int inf=0x3f3f3f3f;
const int N=1e5+5;
const int M=1e9+7;
int kksu(int a,int b){int s=1;while(b){if(b&1){s*=a;s%=M;}a*=a;a%=M;b>>=1;}return s;
}
int f(int n,int i){if(n==0) return 0;int s=0,t=1<<(i+1);n++;s+=n/t*(t/2);if(n%t>t/2) s+=n%t-t/2;s%=M;return s%M;
}
void slove(){int l,r,k;cin>>l>>r>>k;int fz=0,fm=r-l+1;for(int i=0;i<=30,(1ll<<i)<=max(k,r);i++){int v=f(r,i)-f(l-1,i);if(k>>i&1) v=fm-v;fz+=v;fz%=M;}int an=fz*kksu(fm,M-2)%M;cout<<an<<endl;
} 
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;cin>>_;while(_--)slove();return 0;
}

A-約數個數和

樸實無華的題目描述，樸實無華的模板；一開賽就看到好多人都過了，題目還這么簡短；那大概率就是模板了；一開始是毫無頭緒的，因數的分解一直不太會（后來才想明白為什么是除），比賽的時候列了超級多的例子，驚奇的發現我們要求的答案就是 $∑i=1nni\sum_{i=1}^{n}\frac{n}{i}$ ，當時可激動了于是就暴力提交；但是數據很大超時了；于是就把每一項都列了出來，想到了之前看到過的整除分塊，但是之前沒具體學，好在還記得當時的思路自己推了推；

看似很簡單，但是當時寫完d后就一直在推推推…；好在最后還是對了；

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define pii pair<int,int>
#define fi first
#define se second
const int inf=0x3f3f3f3f;
const int N=1e5+5;
void slove(){int n;cin>>n;int an=0;for(int l=1;l<=n;l++){int r=n/(n/l);an+=(n/l)*(r-l+1);l=r;}cout<<an;
} 
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;//cin>>_;while(_--)slove();return 0;
}

整除分塊

什么是整除分塊？

整除分塊 (又稱數論分塊) 是一種用于高效計算涉及整除運算的和式的技巧，常見于數論和算法問題中。其核心思想是將求和式中相同的整除結果進行“分塊”,合并計算，從而將時間復雜度從 $O (n)$ 優化至 $O(n)O(\sqrt{n})$ 。

給定一個正整數 $n$ ,如何快速計算以下和式？

$S=∑k=1n?nk?S=\sum_{k=1}^n\lfloor\frac{n}{k}\rfloor$

我們以16為例，現將結果列出來

$i1234567891011121314151616i201065432222111111\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline i & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 \\ \hline \frac{16}{i} & 20 & 10 & 6 & 5 & 4 & 3 & 2 & 2 & 2 & 2 & 1 & 1 & 1 & 1 & 1 & 1 \\ \hline \end{array}$

觀察整除結果：對于 $k∈[1,n]k\in[1,n]$ , $?nk?的取值最多只有2n\left\lfloor\frac nk\right\rfloor\text{的取值最多只有}{2\sqrt{n}}$ 種(因為 $k≤n時有n種取值，k>n時?nk?≤n)k\leq\sqrt{n}\text{時有}{\sqrt{n}}\text{種取值，}{k>\sqrt{n}}\text{時}{\left\lfloor\frac nk\right\rfloor\leq\sqrt{n}})$ 。

合并相同值：找到所有滿足 $?nk?=q的連續區間?[l,r]\left\lfloor\frac nk\right\rfloor=q\text{的連續區間 }{[l,r]}$ ,計算該區間的貢獻為 $q?(r?l+1)q\cdot(r-l+1)$ 。

確定右端點：對于當前分塊的左端點 $l,其右端點為r=∣nq∣l\text{,其右端點為}r=\left|\frac nq\right|$ ,其中 $q=?nl?q=\left\lfloor\frac nl\right\rfloor$ 。

看不懂？沒關系來數形結合，畫出 $16i\frac{16}{i}$ 的函數圖像，就是我們熟悉的反比例函數的圖像；因為計算機的除法會向下取整，所以我們畫出向下取整的函數，不難發現也是一段一段的！
與我們發現的規律一致；

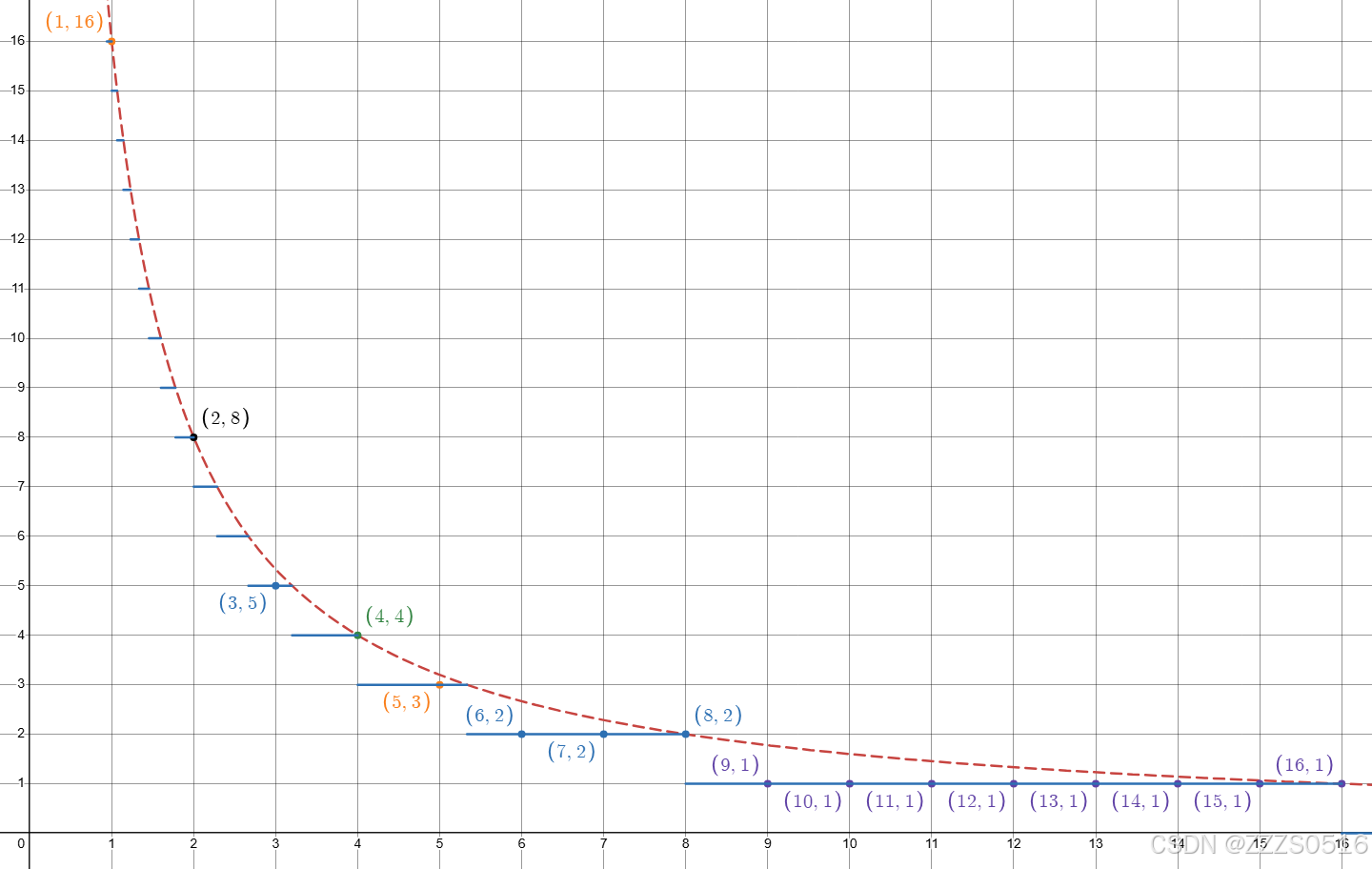
所以整除分塊就是找到這些連續的塊的左右端點，這樣求和的時候就不用每個數都遍歷一遍了；

我們可以這么理解，因為是向下取整，所以順序遍歷新得到的結果的數可能是除不盡的（可能會有余數），那我們就反除這個結果，得到恰好能除完的位置，那個位置就是我們的右端點；再往后就是新的結果了；

分塊過程還是以16為例

分塊區間 [l, r]	q = $?16l?\left\lfloor\frac{16}{l}\right\rfloor$	右端點 $\left\lfloor\frac{16}{q}\right\rfloor$	貢獻 $\cdot (r - l + 1)$
[1, 1]	16	1	16 × 1 = 16
[2, 2]	8	2	8 × 1 = 8
[3, 3]	5	3	5 × 1 = 5
[4, 4]	4	4	4 × 1 = 4
[5, 5]	3	5	3 × 1 = 3
[6, 8]	2	8（因為 $?162?=8\left\lfloor\frac{16}{2}\right\rfloor = 8$ ）	2 × 3 = 6
[9, 16]	1	16	1 × 8 = 8

所以就能得到模板

for(int l=1;l<=n;l++){int r=n/(n/l);an+=(n/l)*(r-l+1);l=r;
}

同類練習

K-取模_2022年中國高校計算機大賽-團隊程序設計天梯賽（GPLT）上海理工大學校內選拔賽

也是一道數學題；題目要求 $∑i=1n(n%i)\sum_{i=1}^{n}\left(n\%i\right)$ 的結果；

我們可以得出 $n%i=n??ni??in\%i=n-\lfloor\frac{n}{i}\rfloor\cdot i$

我們的問題就可以轉行為 $∑i=1n(n%i)=∑i=1n(n??ni??i)\sum_{i=1}^{n}(n\%i)=\sum_{i=1}^{n}(n-\lfloor\frac{n}{i}\rfloor\cdot i)$ 也就是 $=n2?∑i=1n(?ni??i)=n^{2}-\sum_{i=1}^{n}(\lfloor\frac{n}{i}\rfloor\cdot i)$

只看右邊進而得到 $∑x=lrx??ni?\sum_{x=l}^{r}x\cdot\lfloor\frac{n}{i}\rfloor$ 所以我們要求的就是整除分塊后每一塊的區間和（用等差數列求和）×這一塊的值；最后累加起來用n²減；就可以了；

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define pii pair<int,int>
#define fi first
#define se second
const int inf=0x3f3f3f3f;
const int N=1e5+5;
const int M=998244353;
void slove(){int n;cin>>n;__int128 s=0;for(__int128 l=1,r=1;l<=n;l++){int k=n/l;r=n/k;s+=((l+r)*(r-l+1)/2*k+M)%M;l=r;}int an=((__int128)n*(__int128)n-s)%M;cout<<an;
} 
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;//cin>>_;while(_--)slove();return 0;
}