實驗設計如何拯救我的 CEI VSR 28G 設計

為了確定總體設計裕量，CEI 28G VSR/100 Gb 以太網設計需要分析 500 萬種通道變化、收發器工藝和均衡設置的組合。蠻力模擬需要 278 天，這顯然超出了可用的時間表。

相反，我們使用實驗設計（DOE）和響應面建模（RSM）將模擬次數減少了 19,000 倍，但產生了同樣有意義的結果。

本文將演示 DOE 和 RSM 在 CEI 28G VSR 設計中的應用。我們將展示創建 DOE、將數據擬合到模型、確定擬合的優度和可靠性，然后使用模型執行“假設”分析、優化設計因素和量化制造變化的影響的過程。

介紹

CEI VSR 28G/100 Gb 以太網鏈路的單位間隔僅為 35.7 ps，是一項具有挑戰性的系統級設計。在本文中，我們介紹了系統設計過程，該流程產生了業界第一個采用 Inphi 的 GearBox 和 CDR 芯片的 100 Gb 以太網 CMOS PHY。抖動預算緊張，并且由于系統中可能存在各種變化，因此有超過 500 萬個系統條件需要檢查和驗證性能。此外，為了確保系統不會設計過度或性能不佳，需要估計制造變化對性能和制造良率的影響。同時實現和優化所有這些目標確實是一項嚴峻的挑戰。

下一代核心路由器和數據中心需要更多的帶寬、更快的速度和更低的功耗。這迫使該行業實施高達 28 Gbps 的線路速度。圖 1 給出了此類接口的示例拓撲，顯示了芯片到模塊應用，其中可插拔光收發器 CFP2 模塊連接到線卡主機 IC。不要被看似干凈的通道所迷惑，這里有很多損傷，并且比特誤差率（BER）容限僅為千萬億位中的一個誤差，這是一個世界級的挑戰。

1：28G VSR 主機到模塊通道圖。

CMOS 設計使 Inphi 能夠將功率包絡降低到競爭對手 SiGe 和 FPGA 解決方案的三分之一和一半的面積。

設計過程中的眾多挑戰之一是確保發射器和接收器能夠在各種通道中運行，包括一些超過 28G VSR 10 dB 主機到模塊通道的通道。這里使用實驗設計（DOE）和響應面建模（RSM）來確定最大允許走線長度、PCB 布線的最佳層、最佳過孔反焊盤尺寸以及由于 IC 工藝、電壓和溫度（PVT）的制造差異而導致的性能下降;封裝阻抗;印刷電路板（PCB）阻抗;以及 Via Stub Length 變化。將解決這些設計目標中的每一個，我們將說明 DOE/RSM 方法如何提供明智的路徑來回答這些問題。

問題是，盡管系統配置的每個模擬只需 4.8 秒即可完成，但要檢查 500 萬個條件則需要 278 天的計算時間才能完成！大型計算場會有所幫助，但如果在探索空間中添加其他因素，或者如果模擬需要更多時間才能完成，則很容易被結果的計算和存儲所淹沒。使用的鏈路仿真方法是一種快速分析方法，用于估計鏈路配置的 1e-12 BER。如果使用逐位時域分析來估計性能，那么仿真時間很容易接近每個 5 分鐘。在這種計算負載下，500 萬個案例只需要 47.5 年的計算時間。在這種情況下，蠻力分析不會是一個非常有效的工具。我們需要找到另一種方式。

理想情況下，如果有一個神奇的方程式，考慮到走線長度、阻抗和工藝拐角等輸入因素，可以準確揭示最終的系統性能，那就太好了。這個神奇的方程式將支持多種分析，如優化、虛擬“假設”分析，以及定位設計以最大限度地減少制造差異影響的能力。

當然，這并不完全可能，但通過將 DOE 與 RSM 結合使用，我們可以實現這一理想。DOE 用于對因子空間進行采樣，RSM 用于創建最適合數據的方程（或模型）。在驗證了模型的正確性之后，我們可以利用它來做上述所有事情，優化、執行“假設”分析，并最大限度地減少制造變化的影響。DOE/RSM 流程在下面的圖 2 中可視化，這是為了強調分析的迭代性質。此外，分析的每個階段都有一定的假設，在獲得滿意的結果之前，需要重新審視和修改這些假設。

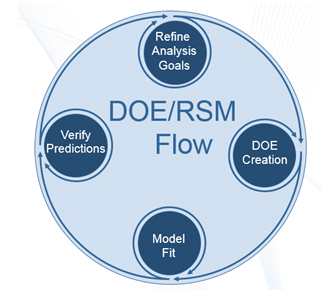
圖 2：實驗設計（DOE）和響應面建模（RSM）方法流程。

分析方法

任何類型分析中最重要的一步都是確定工作的目標。據稱，阿爾伯特·愛因斯坦曾說過：“如果我只有一個小時來拯救世界，我會花 55 分鐘思考問題，而只有 5 分鐘思考解決方案”。同樣，在開始使用 DOE/RSM 方法的實際工作之前，明確定義要解決的問題和答案的準確性水平是絕對必要的。明確的分析目標將使您處于實現目標的最佳位置。

DOE 和 RSM 流程圖強調了分析的迭代性質，因為它允許在過程的每個步驟中完善假設。也可以看出，如果沒有明確的分析目標和退出標準，這樣的做法可能會導致周末的損失和永無止境的評論。

對于一些人來說，一種表示完整性的統計思維方式，即在存在不確定性的情況下做出決策，是令人不舒服的。DOE/RSM 分析將提供置信區間之間的答案，表明結果的準確性，而不是依賴于詳盡的確定分析。詳盡確定的思維方式和統計思維方式之間的唯一區別是，在前者中，任何不確定性都被假裝消失了，而在后者中，不確定性被量化、仔細審查和傳達。無論我們是否愿意，總會存在不確定性，最好的方法是理解它，減少它并接受它。適應不確定性。

請注意，JMP 統計發現軟件用于 DOE 創建和模型擬合分析。本文檔中的許多圖都來自 JMP 報表或源自 JMP 報表。系統鏈路仿真是使用 SiSoft 的 Quantum Channel Designer （QCD）進行的。???

假設

除了思維方式的改變之外，DOE/RSM 技術還需要對所應用的相關統計概念有深入的了解，這可能是一個挑戰。我們將在本文中使用的方法是首先討論一些關鍵概念和其中的假設，然后提供 VSR 28G 接口設計方法的可靠應用示例。

一般來說，對對象進行建模就是利用對感興趣方面的某個方面的簡化描述，從而允許探索對象的特征。一個物理示例是在風洞中使用模型飛機來研究其空氣動力學特性，以幫助設計全尺寸飛機。對我們來說，要建模的對象有點模糊，但通常是系統性能的響應，例如眼高或眼寬在研究因子范圍內的響應。

建模目標是通過對因子空間（如 DOE 表提供）進行采樣來描述真實響應的特征，然后將多項式方程擬合到數據。從這個意義上說，模型實際上是最適合數據的方程。這種模型的一個直觀示例如下圖 3 所示，其中給出了鏈路的眼高與走線長度和阻抗的關系。

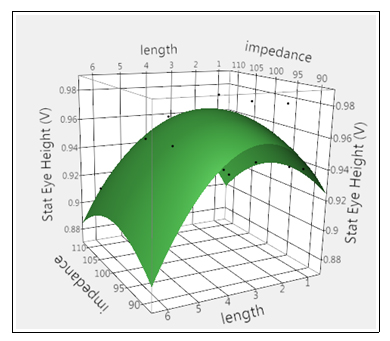
圖 3：眼高響應面示例與走線長度和阻抗的關系。

請注意，該模型只是實際響應的近似值，并且僅在準確的情況下代表現實。此外，從表面的曲率可以看出，該模型是最適合數據的二維拋物線。模型形式和從普通最小二乘擬合中獲得的系數估計值在下面的公式（1）中給出：

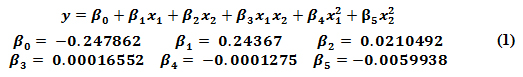
盡管這個表面代表了模型與數據的最佳擬合，但它并沒有解決以下問題：這是表示“真實響應”的最佳模型嗎？在這種情況下，為 length factor 添加更高的多項式項可能會更好地捕獲 trace 的諧振行為。雖然找到絕對最佳模型可能是一個難以捉摸的目標，但我們當然可以通過逐步改進模型形式來實現它。“太簡單”的模型會導致重要的響應特征被平滑化，而“太復雜”的模型會導致過分強調某些響應特征，而犧牲其他更重要的響應特征。

有人可能會認為，要找到最佳模型形式，只需將非常大范圍的多項式項應用于模型擬合，以查看哪些項有效。這種方法的難點在于，可用于擬合的模型形式受響應采樣的限制。如果沿因子維度只有兩個數據樣本，則最多可以有一條直線擬合到數據。如果有三個數據點，則最多可以擬合一條二次線，如果最多有四個數據點，則再擬合一條 3RD階多項式可以擬合。因此，在某些時候，給定一個固定的采樣集，可用于擬合的模型是有限的。這些限制導致這樣一種觀點：因子空間的抽樣還必須考慮模型形式，以便模型擬合可以準確估計真實響應。

從概念上講，使用連續因子可以迭代，直到獲得理想的采樣和模型形式，以實現高質量的模型擬合。但在實踐中，互連的各個部分通常由可能只有離散數量的層級的塊表示，例如以 S 參數模型為特征的連接器系列的情況。在這些情況下，采樣的分辨率是固定的，而高階系統響應特性與低階系統響應特性混疊，從而限制了分析。

模型假設的最后一個方面是多項式可以充分描述響應曲面的想法。還有其他數學上更復雜的模型，例如高斯過程建模，它們具有一些令人驚訝的特性（例如零殘差和空間認知插值），但在這里不討論。作者發現，DOE/RSM 方法的絕大多數信號完整性應用都可以用多項式模型充分描述。

將模型擬合到數據的過程通常由普通最小二乘法（OLS）回歸分析執行。此估計方法假定輸入因子不相關，擬合誤差方差不隨因子或因子水平變化，并且殘差呈正態分布。如果需要，可以放寬這些假設，但需要更復雜的最小二乘法，例如廣義線性模型（允許除正態分布之外的其他殘差誤差分布）和一般最小二乘法（允許相關因子和非均勻誤差方差）。在分析中，我們將對殘差進行廣泛的調查，以確保模型是適當的并且它滿足 OLS 假設。

方法在 28G VSR 系統分析中的應用

該研究的全部目標是回答設計問題并量化 28G VSR 鏈路設計的制造差異。設計問題是，PCB 的哪一層更適合高速布線，最好的 PCB 過孔反焊盤尺寸是多少，以及在足夠的系統性能下仍可以通過的最大 PCB 走線長度是多少？這些問題應該在存在制造差異的情況下得到回答，這也將被量化。

通過使用實驗設計方法對因子空間進行仔細采樣，評估這些 DOE 條件下的系統性能響應，將響應面模型擬合到數據以生成多維方程，然后可用于研究總因子空間。盡管此分析描述暗示了一個簡單的進展，但在實踐中它是相當迭代的，因為每個階段的假設都經過改進，以獲得具有足夠準確性的令人滿意的模型擬合。希望任何眼高和眼寬預測的不確定性小于 +/- 30 mV 和 +/- 0.5 ps。在第一次傳遞時達到所需的準確率很少發生（如果達到，那么它應該引起您的懷疑），但需要對模型假設、因子范圍和 DOE 創建進行細微的修改。

下面的表 1?列出了定義要探索的領域的九個因素。直接影響設計決策的因素稱為設計因素，生產中不可控的因素稱為制造因素。

參數名稱	因子類型	最小值	類型	麥克斯
Tx PVT 角	制造業	不銹鋼	TT	FF 系列
Tx PKG	制造業	90 歐姆	100 歐姆	110 歐姆
線卡 PCB 過孔反焊盤尺寸	設計	32 密爾	36 密爾	40 密爾
線卡 PCB 過孔短線長度	制造業	2 密耳	10 密耳	18 密爾
線卡 PCB 布線層	設計	3	--	9
線卡長度	設計	1 英寸	3 英寸	6 英寸
線卡 TL 阻抗	制造業	90 歐姆	100 歐姆	110 歐姆
Rx PKG	制造業	90 歐姆	100 歐姆	110 歐姆
Rx PVT 角	制造業	不銹鋼	TT	FF 系列

表 1：28G VSR 接口因子空間定義。

設計實驗

傳統上，有幾種方法可以對大型多維因子空間進行采樣。其中一些方法包括窮舉抽樣，其中評估每個條件;隨機抽樣，其中許多條件是偶然選擇的;以及一次抽樣一個因子，其中從名義條件中，每個因子都被孤立地掃描。任何類型抽樣的目標都是獲得總因子空間的表示，以便通過使用樣本的統計數據來推斷總因子空間。窮舉抽樣方法很好，但很可能是一種不切實際的方法。隨機抽樣方法（也稱為蒙特卡洛抽樣）可能是無偏的，但不能保證覆蓋整個空間，并且需要許多采樣點來確保考慮因子空間的所有區域。最后，一次抽樣一個因子（有時稱為 OFAT）會錯過許多重要的因子交互作用。

試驗抽樣設計方法嘗試對空間進行抽樣，以提供整個因子空間的良好覆蓋，同時最大限度地減少游程數。這是通過從隨機采樣開始，然后修改每個采樣點，直到 DOE 集的覆蓋范圍足夠來實現的。采樣的覆蓋率由樣本預測方差量化，這可以通過一些簡單的矩陣作輕松計算。預測方差的這種量化允許量化抽樣的不確定性，從而優化采樣。這就是為什么有些人稱 DOE 方法為最佳設計。

對于我們的 VSR 示例，使用 256 次游程對 9 個因子進行抽樣，并使用 D 最優方法使樣本的預測方差最小。D 最優設計對因子空間的邊的采樣比對中心更多的采樣，并且比其他最優性標準更準確地給出了模型參數估計。由于目標之一是找到因子空間的最壞情況（這些條件通常發生在空間的邊緣），因此準確估計因子空間的邊緣和角落非常重要。采樣的假設模型為 2ND1 的 order 多項式圣對所有因子之間的交互進行排序。

運行模擬并處理模型擬合后，模型擬合預測的準確性將通過置信區間進行量化。較小的置信區間將比較大的置信區間提供更多的保證。置信區間大小取決于三個因素：所需的置信水平（95%、99%、99.9% 等）、模型擬合誤差和 DOE 采樣的覆蓋率。在分析的 DOE 創建步驟中，了解 DOE 采樣的覆蓋率可以深入了解相對置信區間大小，并體現在預測方差中。雖然可視化 9 維空間是一項壯舉，但我們可以用設計空間圖的一小部分來總結整個空間的預測方差，如下圖 4 所示。

圖 4：設計空間分數圖，顯示空間分數上的 DOE 預測方差。

此圖顯示 50% 的因子空間的相對預測方差小于 0.19。雖然該指標的相對性質并不適合作為絕對的指導方針，但它允許對競爭設計進行比較。因此，建議生成一些設計，然后進行比較以選擇最佳設計。

理想的設計（有時稱為正交設計）是指能夠獨立計算參數估計值的設計。這僅適用于選定的設計，并且在大多數情況下（考慮到游程數和模型形式）無法進行正交設計。不過，設計可能接近正交特性。當設計不是正交的時，兩個或多個參數效應彼此之間會略微相關，并且在一定程度上無法區分。在下面圖 5 中的相關圖上的彩圖中，我們模型的所有 54 項的相關程度都可以量化。每個模型項的名稱都為圖的每一列給出，并且每個相應的行的名稱相同。圖中的顏色范圍從藍色（不相關）變為紅色（完全相關）。圖的紅色對角線表示每個模型項都與自身完全相關，正如預期的那樣，但最重要的是，沒有紅色的非對角線項，這表明設計不佳。

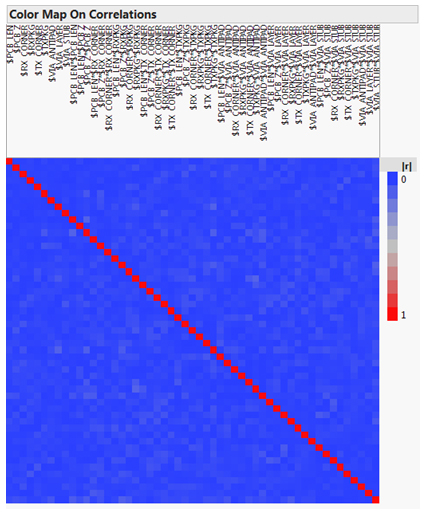
圖 5：響應曲面設計中所有項的相關圖上的色圖。理想情況下，兩個非對角線項之間的相關性為零，用藍色表示。

為了將即將到來的模型擬合置于最佳位置，實驗抽樣設計找到了一個樣本集，該樣本集充分覆蓋了因子空間，并允許對參數效應進行幾乎獨立的估計。

評估系統響應

將 DOE 采樣條件引入 28G VSR 拓撲的 EDA 鏈路仿真環境中，進行仿真并計算鏈路性能指標。這里將考慮的指標是 BER 為 1e-12 時的眼高和眼寬。必須檢查仿真結果波形的一致性和準確性。建議檢查性能中的異常值，以確保它們體現真實的結果。在模型擬合期間，將假定每個條件都代表實際響應，因此任何差異都會將誤差傳播到模型擬合中，并導致分析結論不佳甚至錯誤。下面的圖 6 是如何在 SiSoft 的 Quantum Channel Designer ? （QCD）中可視化結果的示例。

圖 6：在進行模型擬合之前，必須仔細評估仿真結果，以確保所有結果都是合理的。

響應曲面模型擬合

到目前為止，已采取的所有預防措施都已完成，以獲得良好的模型擬合。一旦擬合完成并測量了其質量，將確定這些預防措施是否足夠，或者是否需要更多的迭代和改進。我們將使用的模型形式稱為響應面模型，是一個具有交互項的多維多項式，如下面的方程（2）所示。這是測得的響應（例如眼睛高度）是 n=9 個因子之一，而是未知模型系數，將通過最小二乘法估計。

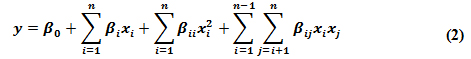
模擬的眼高與響應方程預測的眼高之間的差值稱為誤差殘差。通過檢查殘差，我們可以獲得模型質量的幾個度量并驗證假設。

擬合優度

最簡單的擬合度量稱為多重決定系數，但大家簡稱為“R 平方”，寫成 R2.此指標的范圍從 0 表示擬合差到 1 表示擬合良好。從概念上講，100*R2可以看作是模型中可以解釋的數據變異的百分比。一個有趣的事實是 R2如果添加其他模型術語，則無論這些新術語是否實際重要，指標都將始終提高。修改后的 R2metric 調用的R2調整，會考慮模型中使用的項數，并對任何額外的不必要項進行懲罰。因此，R2和 R2adjusted 表示模型中存在不必要的項。

擬合的誤差標準差可以通過以下方法估計：取數據集中每個點的殘差，對其進行平方，找到平均值，然后取平方根。此 RMSE 指標還可用作預測置信區間的快速估計值。對于 95% 置信區間估計值，只需將 RMSE 乘以 2 即可。如果 +/- 此值大于所需的精度，則有必要返回并重新訪問之前的假設，例如在 DOE 創建中使用的模型形式和因子空間定義。

?7：眼高（左）和眼寬（右）的擬合優度摘要。

如上圖 7 所示，是眼高和眼寬擬合的 JMP 統計軟件擬合匯總。我們看到 R2和 R2調整后的值為 90 年代，眼高的 RMSE 為 22 mV，眼寬為 0.45 ps。

最后，需要檢查擬合誤差殘差本身，以確保它是正態分布的并且不包含任何“結構”。下面的圖 8 顯示了眼高度和寬度的殘差分布，可以看作是大致呈正態分布的。

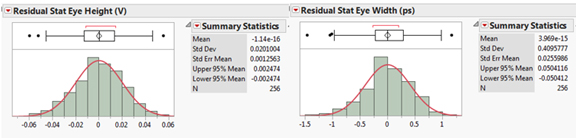
圖 8：眼高（左）和眼寬（右）的擬合誤差殘差。這些表明殘差大致按要求呈正態分布。

殘差與響應或其他重要因子的圖是在殘差中搜索 “structure” 的最佳方式。結構，即殘差和一些解釋變量之間的一些系統關系，是模型偏差的證據，可以提供關于模型擬合中應包含哪些新項的線索。通常，由于 DOE 的采樣不足，此類附加模型項無法立即使用，并且需要重新表述 DOE 創建，以便可以添加額外的模型項而不會使其他重要影響混疊。圖 9 的下方是殘差與響應的圖。無論如何觀察，殘差都應該呈正態分布，但從圖中可以看出，預測的最低眼高情況具有正殘差，如圖中圈出的那樣。進一步的研究表明，額外的模型項 PCB_LEN*PCB_Z*RX_CORNER 改善了擬合度。盡管可能有更多這樣的模型項可以提高擬合度，但準確性足以滿足研究的需要，并且模型擬合被認為足夠好。

圖 9：殘差與預測的眼高（左）和預測的眼寬（右）。殘差中的系統結構表明模型偏差。請注意，最低眼高性能情況都具有正殘差，這一觀察結果導致包含一個額外的模型項，從而提高了擬合度。

雖然這些是非常好的模型擬合結果，但考慮剩余不確定性的來源還是很有趣的。殘差只能來自兩個來源，隨機誤差和失擬。對于確定性信號完整性仿真，沒有隨機噪聲，因此殘差完全是由于缺乏擬合造成的。在實踐中，之所以無法實現完美的模型擬合，是因為潛在現象不是完美的多項式，還因為真正的潛在現象因子是亂碼，僅由研究因子不完美地表示。

探索和優化 28G VSR 系統

一旦完成了所有作以確保正確擬合，我們就可以探索模型所表示的因子空間，并確信不確定性已大致理解。在此應用程序中，可視化 10 維空間是一項艱巨的任務，幸運的是，有一些工具可以促進這種類型的分析。一個稱為預測刻畫器的圖顯示如果所有其他因子都保持不變，每個因子的響應將是什么。這種類型的繪圖在交互使用時最有用，但也可以從下面使用的靜態視圖中收集到很多信息。例如，考慮兩個因子 RSM 擬合的預測刻畫器圖，如圖 10 所示。

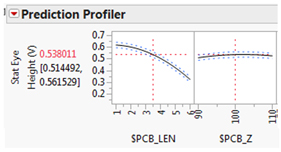
圖 10：預測眼高響應的預測刻畫器示例圖。它顯示了在所有其他因子保持不變的情況下，相對于每個因子的響應。

此預測刻畫器圖顯示了跨解釋因子、走線長度（PCB_LEN）和走線阻抗（PCB_Z）的眼高響應。由于跡線長度因子的斜率最大，我們可以說這是因子空間的這個區域中影響最大的因子。如果因子之間存在任何交互作用，則線的有效斜率可能會在因子空間的其他區域中發生變化。此外，該圖表明，當 PCB_LEN=3.5 且 PCB_Z = 100 時，預測的眼高為 0.538 V，95% 置信區間為 [0.514， 0.562] V，這相當于表示預測的眼高為 0.538 +/- 0.0234 V，置信區間為 95%。置信區間在預測刻畫器圖中由黑色實線預測響應周圍的藍色虛線表示。

置信區間（有時縮寫為 CI）可以被認為傳達以下信息：

置信區間為真實響應提供一系列合理值，超出該范圍的值相對不可信，或者
CI 給出估計的精度，其中上限和下限提供可能的最大估計誤差，盡管可能存在更大的誤差。

95% 的置信水平大致涵蓋與預測值的 2 個標準差，而 99.5% 的置信水平大致涵蓋與預測值的 3 個標準差。圖 11 給出了示例因子空間中間的預測刻畫器圖。

圖 11：眼高（頂行）和眼寬（底行）因子空間中間的預測刻畫器。重要因素可以通過曲線的斜率來識別

如前所述，走線長度是該空間區域中影響最大的因素。這兩行圖分別用于眼睛高度和眼睛寬度。如果希望了解某個因子對空間的這個區域的影響，此圖很容易提供此信息。

由于擬合的響應表面由定義明確的函數表示，因此可以在空間中搜索最壞情況，如圖 12 中的預測刻畫器圖所示。

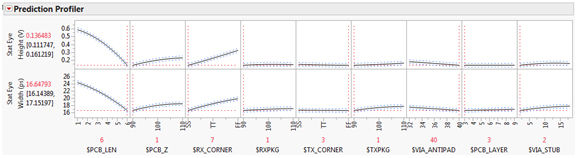
圖 12：在預測的最壞情況下，眼睛高度（頂行）和眼睛寬度（底行）的預測剖面圖。

需要注意的是，雖然走線長度仍然是空間這個區域最有影響力的因素，但與它們在因子空間中間的影響相比，走線阻抗和接收器 PVT 拐角（$RX_CORNER）也變得有些影響。

確定高速信號的 routing 層

這里使用的設計優化策略是首先確定最壞情況的制造條件，然后將設計因素置于最佳情況條件下，以最大限度地減少最壞情況性能的影響。

為了量化 PCB 布線層在最壞情況拐角處的影響，計算了 PCB_LAYER=3 和 PCB_LAYER=9 的預測響應并進行比較。如下圖 13 所示（請注意，縱軸已縮放以提供更好的視圖），兩個 PCB 層之間的眼高和眼寬差僅為 0.012 mV 和 0.35 ps。另請注意，眼高的 95% 置信區間為 +/-24 mV，眼寬的 95% 置信區間為 +/- 0.5 ps。當預測的差異小于置信區間時，可以說模型無法自信地將效應識別為顯著，并且沒有提供任何可作的信息。這可能會得出以下結論：

PCB routing 層是系統性能的弱預測器，第 3 層和第 9 層是等效的，或者
PCB routing layer 9 與 layer 3 相比具有輕微但不顯著的優勢。

如果這些結論中的任何一個都不足，那么將需要有關這兩個層的影響的額外信息來做出明確的決定。可以圍繞該因子定義一個更集中的 DOE/RSM，其中從研究中刪除了一些其他不重要的因子，以提高分析的準確性。此外，在做出任何決策時，應考慮對 routing layer 決策的其他影響，例如 PCB 空間成本或金錢成本。

對于 VSR 研究，將得出結論， PCB 布線層 9 比第 3 層略有優勢（盡管在統計上不顯著）。

圖 13：如何評估整個 PCB 層因子的“假設”場景的示例。左側的曲線顯示了 PCB 布線層位于第 3 層時的預測響應，右側的曲線顯示了當 PCB 布線層位于第 9 層時的預測響應。

確定最佳過孔反焊盤尺寸

將采用類似的方法來了解 PCB 對反焊盤尺寸的影響。對于眼高，32 和 40 mil 的反焊盤直徑之間的鏈路性能差異為 45 mV 和 0.47 ps，其中眼高置信區間為 +/- 25 mV，眼寬置信區間為 +/- 0.5 ps，置信度為 95%。從圖 14 中的預測刻畫器圖中可以直觀地看出這一點，因為眼高圖的紅色水平虛線不包含在藍色虛線置信區間線中，而紅色虛線包含在眼寬的藍色置信區間虛線中。因此，我們可以得出結論，32 mils 的反焊盤尺寸是眼高的更好解決方案，并且可能是眼寬性能的更好解決方案，但在統計上無關緊要。在做出最終決定之前，應仔細權衡其他限制，例如制造給定的防焊盤直徑時增加的制造問題。

對于這項研究，未來的分析將使用 32 mils 的反焊盤尺寸。

圖 14：跨過孔反焊盤因子的“假設”分析，顯示了不同過孔反焊盤尺寸之間的性能差異。

需要澄清的一點是，雖然 DOE/RSM 方法可以量化給定因素的影響，但它無法說明原因。在給定情況下，某個因素有影響的原因必須來自主題專業知識和工程判斷。如果沒有令人滿意的物理解釋，那么重要性的統計指示可能是進一步分析的動力，并且對數據的競爭性物理解釋做出假設可能很有用。

制造變化

量化制造變異的一種方法是為每個因子分配概率分布函數?（PDF），然后隨機生成數百萬個案例。利用響應面方程，可以量化每個隨機情況的系統性能，并用于指示產生特定系統性能水平的概率。必須非常小心才能獲得準確的 PDF，因為尾部的權重會在此類分析中產生很大差異。圖 15 顯示了預測刻畫器圖和分配給每個制造因子的 PDF。

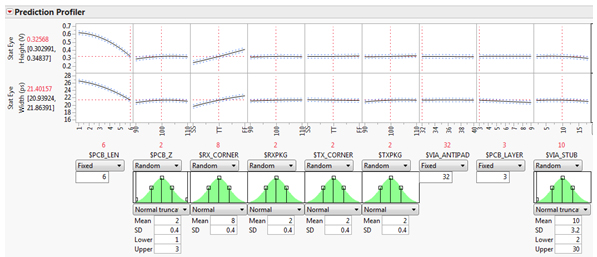
圖 15：預測刻畫器圖，其中分配了分配給每個制造因子的分布。根據這些分布對因子空間進行隨機抽樣將提供制造 Yield 信息。

希望將制造變化理解為線卡走線長度的函數。因此，對于 1 、 2 、 3 、 4 、 5 和 6 英寸的線卡長度，隨機生成 100 萬個案例，并使用響應面方程計算眼高和眼寬性能。圖 16 中給出了每種長度的 100 萬個案例的平均值和標準差。該分析清楚地表明，對于眼高，制造變化的影響隨著線卡走線長度的增加而增加。增加的一個可能解釋不是當線卡走線長度等于 6 英寸時會發生更多的制造變化，而是系統更容易受到上述變化的影響。還應注意的是，眼寬變化隨軌跡長度的增加而變化非常小。圖 16：制造良率預測與最大允許的跡線長度。豎條表示每個產量分析的標準差，并顯示眼高變異性隨著痕量長度的增加而增加。

每百萬缺陷數分析

最后一項分析是對每百萬個缺陷數的估計。如果因子 PDF 和響應面方程是準確的，則可以計算系統的制造良率。此分析的通過/失敗標準取決于模擬中包含的鏈接不確定性以及預算中的鏈接不確定性。在本例中，通過系統的規格限值為 200 mV 的眼高和 19 ps 的眼寬。對于線卡長度為 6 英寸的系統，眼高和眼寬的產量分布圖如下圖 17 所示。

圖 17：每百萬缺陷數（DPM）分析，根據眼高和眼寬要求分別顯示預測的 225 和 170 DPM。

此處，規格下限（LSL）繪制在分布上，顯示了低于此限值的分布百分比以及相應的百萬分之幾（PPM）值 224 和 170 個/百萬缺陷。

結論

我們已經展示了有助于第一個 CMOS 28G VSR / 100G 以太網 PHY 設計的方法。接口設計問題：要布線的 PCB 層、使用多大尺寸的過孔反焊盤以及允許的最大走線長度。確定了最壞的情況，并量化了制造變化對性能的影響。所有這些都是通過 DOE/RSM 方法完成的。DOE 無需數月的計算時間來模擬數百萬種情況，而是僅用 256 次運行就對因子空間進行了智能采樣。最小二乘模型擬合找到與數據最擬合的響應曲面，在驗證模型后，它用于預測整個因子空間的系統性能。必須強調的是，隨著模型假設的變化，需要對方法進行多次迭代。總體而言，DOE/RSM 方法已被證明是理解和優化令人眼花繚亂的大因子空間的強大方法，并為 Inphi 的成功做出了貢獻，推出了世界上第一個生產就緒的 100G CMOS PHY/SerDes 變速箱。