插入排序

算法思想

每次將?個待排序的記錄按其關鍵字大小插入到前面已排好序的子序列中，直到全部記錄插入完成。

代碼實現

void InsertSort(int A[],int n){int i,j,temp;for(i = 1;i<n;i++){if(A[i]<A[i-1]){temp = A[i];			//用temp暫存A[i]for(j=i-1;j>=0&&A[j]>temp;--j)		//檢查所有前面已經排好序的元素A[j+1]=A[j];				//所有大于temp的元素都往后挪一位A[j+1]=temp;					//復制到插入位置}}
}

代碼實現（帶哨兵）

void Insert(A[],int n){int i,j;for(i = 2;i<=n;i++){if(A[i]<A[i-1]){A[0]=A[i];for(j=i-1;A[0]<A[j];--j)A[j+1]=A[j];A[j+1] = A[0];}}
}

優點：不需要每輪循環都判斷一次j>=0

算法效率分析

時間復雜度	空間復雜度	穩定性
O(1)	主要來自對比關鍵字、移動 元素（若有n個元素 則需要 n-1 趟處理）	穩定
	最好情況：每次只需要對比一次 不需要移動→O(n)
	最壞情況：原本都是逆序排放的 → O(n2)
	平均時間復雜度：O(n2)

優化 – 折半插入排序

先用折半查找找到應該插入的位置，再移動元素

當low>high時折半查找停止，并將low之后的元素全部右移，并將A[0]復制到low所在位置

為了保證算法的穩定性，當A[mid]=A[0]時，應繼續在mid所指的右邊尋找插入位置

void InsertSOrt(int A[],int n){iint i,j,low,high,mid;for(i=2;i<=n;i++){A[0]=A[i];low = 1;high = i-1;while(low<=high){mid = (low+high)/2;if(A[mid]>A[0]) high = mid-1;else low=mid+1;}for(j=i-1;j>=high+1;--j)A[j+1]=A[j];A[high+1]=A[0];}
}

比起“直接插入排序”，比較關鍵字的次數減少了，但是移動元素的次數沒變，整體來看時間復雜度仍未O(n²)

希爾排序

算法思想

先將待排序表分割成若干形如 L[i, i + d, i + 2d,…, i + kd] 的“特殊”子表，對各個子表分別進行直接插入排序。縮小增量d，重復上述過程，直到d=1為止。

……

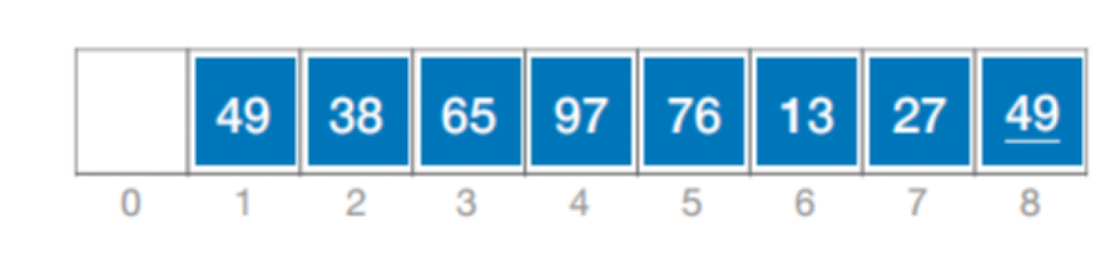
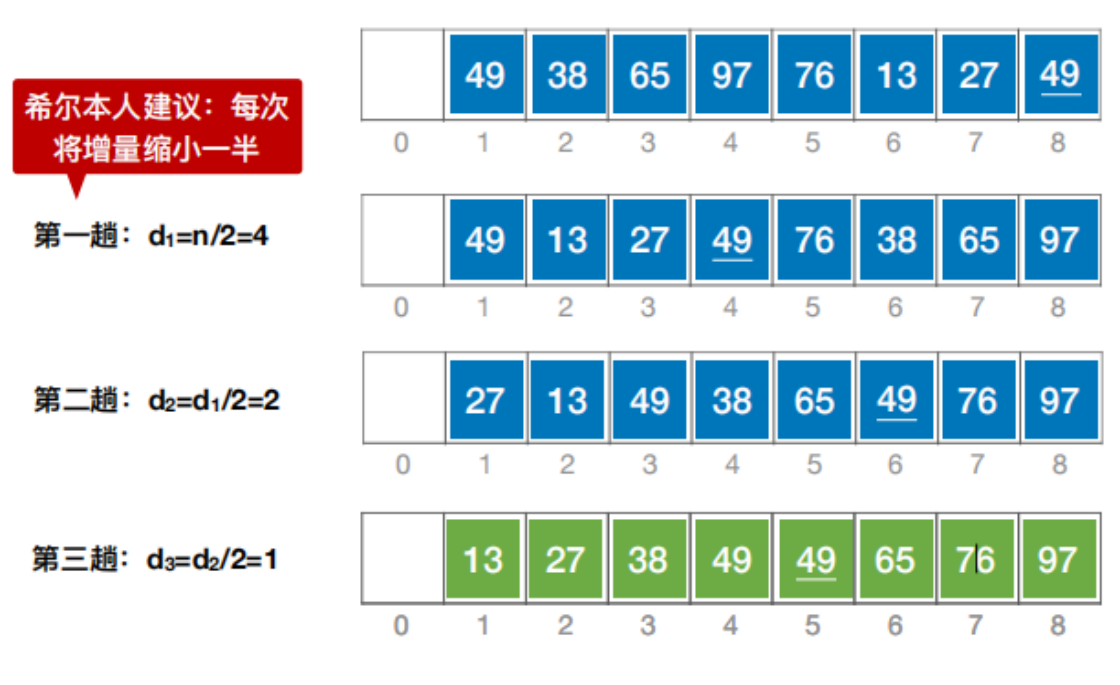
//希爾排序
void ShellSort(int A[],int n){int d,i,j;//A[0]只是暫存單元，不是哨兵，當j<=0時，插入位置已到for(i=d/2;d>=1;d=d/2)for(i=d+1;i<=n;++i)if(A[i]<A[i-d]){A[0]=A[i];for(j = i-d;j>0&&)}
}

目前無法用數學?段證明確切的時間復雜度 ，最壞時間復雜度為 O(n2)，當n在某個范圍內時，可達O(n1.3)

穩定性：不穩定

適?性：僅適?于順序表，不適?于鏈表