? ? ? ? 大家好，今天還是繼續我們的動態規劃里面的背包問題，前面我們主要接觸的是0-1背包和完全背包，其實這兩個背包問題主要就是看看每一件物品我們是否有多件，如果每一件物品我們只能取一次的話那這樣我們就是0-1背包，如果每一件物品我們可以取多件的話那這樣就是完全背包，那我們就接著以前的來繼續我們今天的題目。

第一題對應力扣上編號為322的題目零錢兌換

? ? ? ? ? 這道題大家聽到題目名字應該就會有種熟悉的感覺，我們是不是前面做過，是的我們前面的確做過一道關于零錢兌換的題目，而且我們在貪心算法章節還刷過一道叫做檸檬水找零的題目，那我們看看這道題目跟我們以前做過的有什么不一樣的：

? ? ? ? 其實這道題目的背景與我們前面的那道零錢兌換的題目是一樣的，不過那道題目讓我們求的是可以湊出給定數額的組合方案數，而這一道題目讓我們求的是湊出給定數額的所需的最少硬幣個數，其實很明顯題目還是很經典的完全背包問題，因為我們每種硬幣的數量是無限的，但本題和純完全背包不一樣，純完全背包是湊成背包最大價值是多少，而本題是要求湊成總金額的物品最少個數！那我們還是嘗試使用完全背包問題來解決，還是動用動規五部曲。

? ? ? ?首先動規五部曲的第一步就是確定dp數組的含義，其實這里的話我們使用一維dp數組就可以了，dp[j]：湊足總額為j所需錢幣的最少個數為dp[j]。

? ? ? ?第二步就是確定遞推公式，我們需要仔細考慮一下，因為題目要求我們去求湊出給定金額的最少的錢幣數，所以我們可以大致猜測肯定要出現取min值，我們很容易知道湊足總額為j - coins[i]的最少個數為dp[j - coins[i]]，那么只需要加上一個錢幣coins[i]即dp[j - coins[i]] + 1就是dp[j]（考慮coins[i]，那如果不考慮coins[i]呢？那就是dp[j], 那這樣兩個取最小值不就是我們的遞推公式了。

? ? ? ?第三步就是初始化dp數組，我們首先湊足總金額為0所需錢幣的個數一定是0，那么dp[0] = 0;

這個是很明顯的，考慮到遞推公式的特性，dp[j]必須初始化為一個最大的數，否則就會在min(dp[j - coins[i]] + 1, dp[j])比較的過程中被初始值覆蓋。因為我們每一次都要取最小值，這樣可以保證每次都可以正確更新所需的最少錢幣數。

? ? ? ? 第四步就是確定遍歷順序，本題求錢幣最小個數，那么錢幣有順序和沒有順序都可以，都不影響錢幣的最小個數。那其實我們先遍歷錢幣再遍歷金額是可以的，反過來也是可以的。

? ? ? ? 還有一步比較重要的就是舉例推導dp數組，以代碼隨想錄的例子為例：

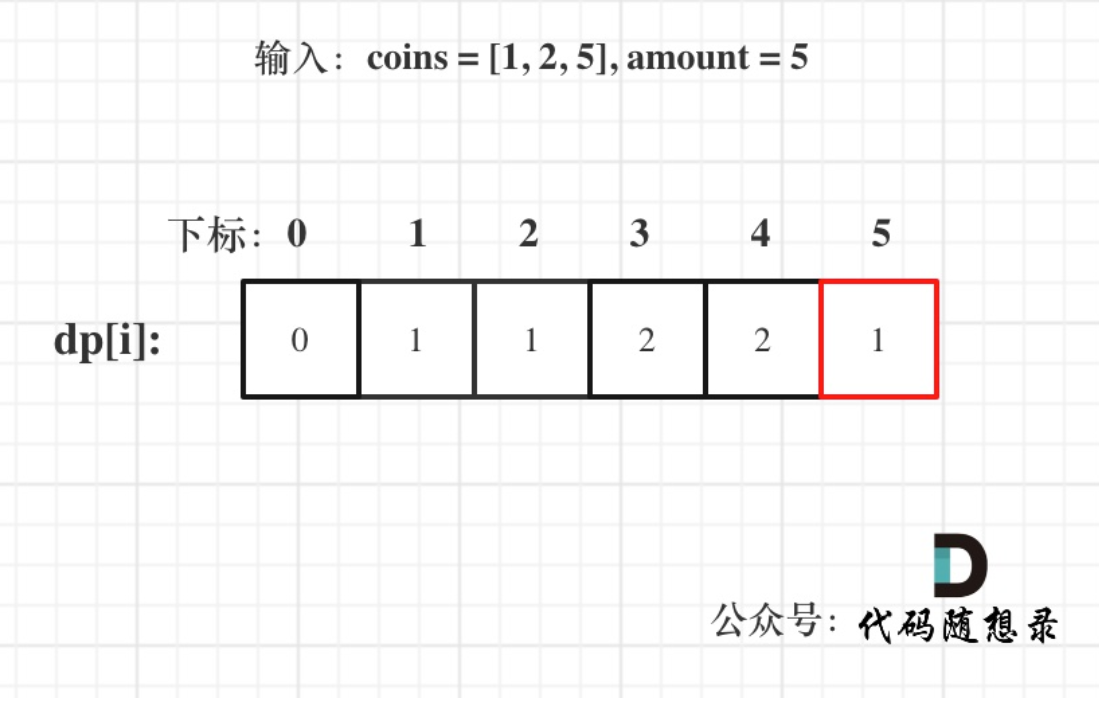
? ? ? ? ? ?那我們可以嘗試給出代碼：

class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX);//初始化dp數組dp[0] = 0;//先遍歷錢幣再遍歷總額for (int i = 0; i < coins.size(); ++i){for (int j = coins[i]; j <= amount; ++j){//如果被更新了就說明存在最少的硬幣數而且可以被湊出if (dp[j - coins[i]] != INT_MAX){dp[j] = min(dp[j - coins[i]] + 1, dp[j]);}}}if (dp[amount] == INT_MAX) return -1;return dp[amount];}
};

?第二題對應力扣編號為279的題目完全平方數

? ? ? ? ?這是我們今天的第二題，這道題我們以前沒有見過比較類似的背景，我們就直接看看這道題目的要求：

? ? ? ? 讀完題目之后我就知道了，其實就是湊出這個數我們至少需要幾個完全平方數，這個題目似乎與上一道題目比較類似，其實都是填滿背包至少需要多少件物品類型題目，很明顯這個題目還是完全背包，那我們還是得用動規五部曲來解決。

? ? ? ? 第一步還是確定dp數組的含義，dp[j]：和為j的完全平方數的最少數量為dp[j]。

? ? ? ? 第二步就是遞推公式，這道題目的遞推公式與上一道題目的遞推公式是異曲同工，還是我們考慮我是是否使用當前的完全平方數，當然我們不需要去寫一個函數判斷一個數是不是完全平方數，這里的每一個數就相當于我們上一道題的錢幣金額，所以我們的遞推公式大家或許就知道了應該是dp[j] = min(dp[j - i * i] + 1, dp[j])。

? ? ? ? 第三步一樣的思路還是dp數組的初始化，dp[0] = 0其實這里可能有同學存在疑問，明明0*0 = 0那為啥dp[0] = 1不對呢，看題目描述，找到若干個完全平方數（比如 1, 4, 9, 16, ...），題目描述中可沒說要從0開始，dp[0]=0完全是為了遞推公式。所以其實這個dp[0] = 0沒有什么意義，從遞歸公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要選最小的，所以非0下標的dp[j]一定要初始為最大值，這樣dp[j]在遞推的時候才不會被初始值覆蓋。這里其實與我們上面的題目也是類似的。

? ? ? ?第四步就是確定遍歷順序，我們還是使用完全背包的思路，先遍歷物品再遍歷背包就可以了。

? ? ? ? 第五步就是打印驗證dp數組這里就不說了，這個大家可以自行去測試。接下來走完動規五部曲以后我們就可以寫出這道題目的解題代碼：

class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1, INT_MAX);dp[0] = 0;//遍歷物品for (int i = 1; i <= n; ++i){//遍歷背包其實也就是我當前使用完全平方數和湊出來的和for (int j = i * i; j <= n; ++j){//這是我們的遞推公式，如果我想用一個i * i湊出的完全平方數就得先看前面那個數的需要//完全平方數的個數然后加1就可以了dp[j] = min(dp[j - i * i] + 1, dp[j]);}}return dp[n];}
};

第三題對應力扣編號為139的題目單詞拆分

? ? ? ?這是我們今天的最后一道題目，我們動態規劃章節似乎也沒有遇到過背景相似的題目，所以我們就先看看題目的要求：

? ? ? ?題目是給我們一個字符串列表里面存放了一些單詞，給定我們一個字符串，看看這個字符串是否可以由我們字符串列表里面的單詞拼接出來，而且字符串列表里面的單詞都是可以重復使用的，很明顯這還是一道完全背包的問題，那我們還是使用動規五部曲來解決這道題目。

? ? ? 第一步確定dp數組以及下標的含義：dp[i] : 字符串長度為i的話，dp[i]為true，表示可以拆分為一個或多個在字典中出現的單詞。這題目有點特殊，所以我們定義的dp數組也是有點奇怪，第一次出現過bool類型的dp數組。

? ? ? ?第二步就是我們的確定遞推公式，這或許很奇怪，既然我們的dp數組都定義成了bool類型的那我們還有什么遞推公式，其實是這樣的：如果確定dp[j] 是true，且 [j, i] 這個區間的子串出現在字典里，那么dp[i]一定是true。（j < i ）。這個聽起來很抽象其實不難理解，我們dp[j]已經湊出了，只要我們[j,i]的區間里面存在我們長度為j與長度為i相差的字符串，那不就說明長度為i的字符串也可以被湊出了。這個思路很有趣，大家要好好積累一下。

? ? ? ?第三步是dp數組如何初始化，從遞推公式中可以看出，dp[i] 的狀態依靠 dp[j]是否為true，那么dp[0]就是遞推的根基，dp[0]一定要為true，否則遞推下去后面都都是false了。大家可以想想其實題目也說了我們的字符串是非空的，其實dp[0]完全是為了遞推公式服務。

? ? ? ?第四步就是遍歷順序，這其實還是一道完全背包的題目，那我們其實還是可以按照完全背包的遍歷順序，其實單詞就是物品，題目所給字符串就是背包，題目還是有需要注意的地方，這道題目是在意順序，其實也就是排列問題而不是組合問題，如何理解？拿 s = "applepenapple", wordDict = ["apple", "pen"] 舉例。"apple", "pen" 是物品，那么我們要求 物品的組合一定是 "apple" + "pen" + "apple" 才能組成 "applepenapple"。"apple" + "apple" + "pen" 或者 "pen" + "apple" + "apple" 是不可以的，那么我們就是強調物品之間順序。所以我們就知道了這道題目我們就只能先遍歷背包再遍歷物品，如果我們先遍歷物品再遍歷背包就會出現亂序的情況，這點大家必須注意。

? ? ? ?那這樣其實題目的代碼與以前似乎還是有些不一樣：

class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {unordered_set<string> wordSet(wordDict.begin(), wordDict.end());vector<bool> dp(s.size() + 1, false);dp[0] = true;for (int i = 1; i <= s.size(); i++) {   // 遍歷背包for (int j = 0; j < i; j++) {       // 遍歷物品string word = s.substr(j, i - j); //substr(起始位置，截取的個數)if (wordSet.find(word) != wordSet.end() && dp[j]) {dp[i] = true;}}}return dp[s.size()];}
};

?今日總結

? ? ? ?我們今天的題目其實有難度，大家得多多思考，理解動態規劃并不容易，尤其是單詞拆分這道題目的確很有難度，我們得理解為什么必須先遍歷背包再遍歷物品，以及我們要區分題目是考察的我們是組合問題還是排列問題，就是看看有沒有順序要求即可，這就是我們今天的講解，我們明天見！?