引言

AVL樹，基于二叉搜索樹通過平衡得到

前面我們知道，通過🔗二叉搜索樹可以便捷快速地查找到數據，但是當序列有序時，就會退化成如下圖所示的單鏈表，搜索效率降低為O(N)，為了解決這個問題，引出了平衡二叉樹（AVL樹）

定義

平衡二叉樹，簡稱AVL樹，它可以是一顆空樹
如果不是空樹，則需要滿足 任何一個結點的左子樹與右子樹高度之差的絕對值不超過1

圖一是AVL樹
圖二不是AVL樹，因為虛線內部分高度差大于1

如何讓二叉樹變成AVL樹呢
答案是通過旋轉（左旋、右旋）操作，在說左旋和右旋操作之前，了解一個概念——平衡因子

是否為AVL樹需要根據結點的左右子樹高度差來判斷，所以引出平衡因子的概念
平衡因子：結點左子樹高度減去右子樹高度
之后我們還可以通過平衡因子來判斷需要哪種旋轉方式（左旋、右旋）

將二叉樹分為四種類型，分別是LL（left）型、RR（right）型、
LR型、RL型
這幾種類型是根據引起不平衡的結點的位置來分的，下面將引起不平衡的這個結點叫做unbalanceNode

旋轉方式

判斷右旋還是左旋，可以這樣理解
向哪個方向旋轉就是讓哪邊樹更高。比如左旋，就是右子樹高于左子樹，要想平衡就要讓左子樹更高一點

LL型

unbalanceNode在根結點左孩子的左子樹 – 根結點右旋

如圖，插入結點5后導致二叉樹失衡，插入的結點5在根結點左孩子14的左子樹上，所以就是 LL 型

LL型二叉樹的平衡因子滿足：
根結點：2
根結點的左孩子：1（左孩子的左子樹高度>右子樹）

方法就是將根結點右旋，意思就是將根結點向右旋轉到其左孩子的右孩子的位置

在根結點向右旋轉的過程中，因為根結點的左孩子14原本有右孩子20，所以根結點就會和20發生沖突，這時需要將14的右孩子20變成根結點的左孩子

根結點25旋轉完成后就是

再和14相連，最終結果：

---

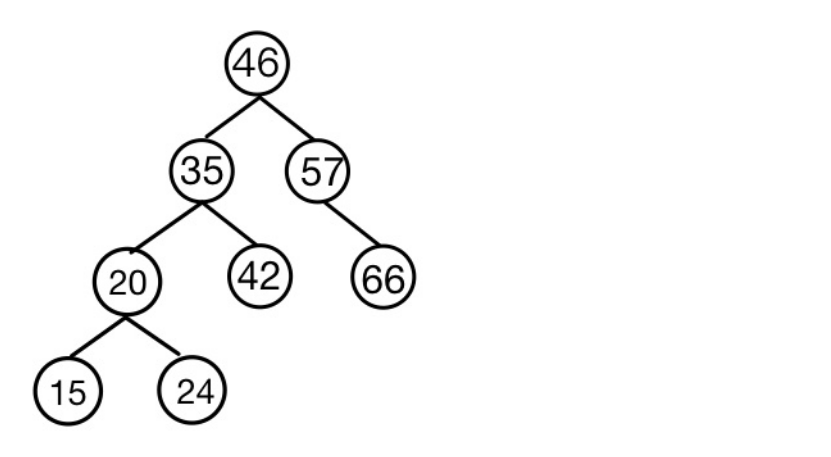
如果出現了多個結點都失衡的情況，如下圖

46、35、24都失衡了，那這時候就不是將根結點右旋了，而是將 與導致失衡的結點（15）最近的失衡結點右旋，在這個例子中也就是將24右旋

再與35相連，最終結果：

---

RR型

unbalanceNode在根結點右孩子的右子樹 – 根結點左旋

RR 型與 LL 型方法一致，只是換湯不換藥

如圖，插入結點67后導致二叉樹失衡，插入的結點67在根結點右孩子45的右子樹上，所以就是 RR 型

RR型二叉樹的平衡因子滿足：
根結點：-2
根結點的左孩子：-1（左孩子的右子樹高度>左子樹）

方法就是將根結點左旋，意思就是將根結點向左旋轉到其右孩子的左孩子的位置

在根結點向左旋轉的過程中，因為根結點的右孩子45原本有左孩子34，所以根結點就會和34發生沖突，這時需要將45的左孩子34變成根結點的右孩子

根結點26旋轉完成后就是

再和45相連，最終結果：

---

如果同時出現了多個失衡結點，和 LL 型一樣，也是找到與導致失衡結點距離最近的失衡的結點，對該結點進行左旋操作

---

LR型

unbalanceNode在根結點左孩子的右子樹 – 先左旋再右旋（根結點的左孩子左旋，根結點右旋）

如圖，插入結點40后導致二叉樹失衡，插入的結點40在根結點左孩子25的右子樹上，所以就是 LR 型

LR型的平衡因子滿足：
根結點：2
根結點的左孩子：-1（左孩子的右子樹高度>左子樹）

方法就是

1. 先將根結點的左孩子左旋
2. 再將根結點右旋

對于這個二叉樹，調整過程：

1. 將根結點的左孩子左旋
   
2. 將根結點右旋后
   

---

RL型

unbalanceNode在根結點右孩子的左子樹 – 先右旋再左旋（根結點的右孩子右旋，根結點左旋）

如圖，插入結點29后導致二叉樹失衡，插入的結點29在根結點右孩子48的左子樹上，所以就是 RL 型

LR型的平衡因子滿足：
根結點：-2
根結點的右孩子：1（右孩子的左子樹高度>右子樹）

方法就是

1. 先將根結點的右孩子右旋
2. 再將根結點左旋

對于這個二叉樹，調整過程：

1. 將根結點的右孩子右旋
   

2. 將根結點左旋
   

實現

結構

結構體中一定包含的是數據data 和左右孩子指針
又因為需要計算平衡因子，所以需要知道左右子樹的高度，直接將高度height 包含在結構體中

// 定義樹結構
type BTNode struct {data   int //數據left   *BTNoderight  *BTNodeheight int //樹的高度
}

獲取結點高度

首先判斷結點 t 為不為 nil， 為 nil 直接返回0

// 獲取結點高度
func (t *BTNode) GetHeight() int {if t == nil {return 0}return t.height
}

平衡因子

平衡因子 = 左子樹高度 - 右子樹高度
若結點 t 為 nil ，直接返回0

// 計算結點的平衡因子 -- 左子樹高度-右子樹高度
func (t *BTNode) GetBalanceFactor() int {if t == nil {return 0}return t.left.GetHeight() - t.right.GetHeight()
}

更新高度

在插入或刪除數據后，根結點和其他結點的高度都有可能發生變化，所以在插入或刪除結點后，需要更新節點的高度，否則在計算平衡因子會出錯

// 更新高度
func (t *BTNode) UpdateHeight() {leftHeight := t.left.GetHeight()rightHeight := t.right.GetHeight()if leftHeight > rightHeight {t.height = leftHeight + 1} else {t.height = rightHeight + 1}
}

左旋

對 node 進行左旋 --> node連接在node.right 的左孩子，如果node.right 原本有左孩子leftChild，那讓leftChild 連接到node 的右孩子

// 左旋
func (t *BTNode) LeftRotate() *BTNode {//新的根結點變為t的右孩子newT := t.right//判斷newT有沒有左孩子if newT.left == nil{  //newT原本沒有左孩子，t為newt.T左孩子newT.left = t}else { //newT原本有左孩子，原本的左孩子變為t的右孩子，t為newT左孩子t.right = newT.leftnewT.left = t}//更新高度t.UpdateHeight()newT.UpdateHeight()return newT
}

對上面的代碼，還可以再簡化
如果newT沒有左孩子，即為nil，也可以直接賦值給t.right

// 左旋
func (t *BTNode) LeftRotate() *BTNode {//新的根結點變為t的右孩子newT := t.rightt.right = newT.leftnewT.left = t//更新高度t.UpdateHeight()newT.UpdateHeight()return newT
}

右旋

對 node 進行右旋 --> node連接在node.left 的右孩子，如果node.left 原本有右孩子rightChild，那讓rightChild 連接到node 的左孩子

// 右旋
func (t *BTNode) RightRotate() *BTNode {newT := t.leftt.left = newT.rightnewT.right = tt.UpdateHeight()newT.UpdateHeight()return newT
}

插入結點

按照二叉搜索樹插入數據的方式插入，再根據平衡因子判斷是否需要調整和調整的方式

// 插入結點
func (t *BTNode) Insert(data int) *BTNode {if t == nil {return &BTNode{data,nil,nil,1,}}//遞歸查找插入位置if data < t.data {t.left = t.left.Insert(data)} else if data > t.data {t.right = t.right.Insert(data)} else {return t //不支持重復數據}//更新當前結點的高度t.UpdateHeight()//檢查是否需要旋轉balance := t.GetBalanceFactor()//左子樹高if balance > 1 {if t.left.GetHeight() == 1 { //左孩子的左子樹高 -- ll型//右旋return t.RightRotate()}if t.left.GetHeight() == -1 { //左孩子的右子樹高 -- lr型//先對左孩子左旋，再對結點右旋t.left.LeftRotate()return t.RightRotate()}}//右子樹高if balance < -1 {if t.right.GetHeight() == 1 { //右孩子的右子樹高 -- rr型return t.LeftRotate()}if t.right.GetHeight() == -1 { //右孩子的左子樹高 -- rl型先對右孩子右旋，再對結點左旋t.right.RightRotate()return t.LeftRotate()}}return t
}

中序遍歷

// 中序遍歷
func (t *BTNode) InOrder() {if t == nil {return}t.left.InOrder()fmt.Printf("%d ", t.data)t.right.InOrder()
}