一、實驗要求與目的

1.復習CCC基本概念，并根據實驗平臺提供的資料完成驗證性實驗。

2.編程練習：以書上例題小模數p為例編程實現ECC的基本運算規則。

二、實驗內容與步驟記錄（只記錄關鍵步驟與結果，可截圖，但注意排版與圖片大小）

ECC的設計思路

ECC（橢圓曲線密碼學）是一種基于橢圓曲線數學的現代加密技術，其設計思路主要圍繞橢圓曲線的代數結構和有限域上的運算特性展開。以下是詳細的設計思路：

1.橢圓曲線的選擇與點的尋找

ECC 的基礎是橢圓曲線，通常表示為 y2=x3+ax+b 的形式，其中 a 和 b 是曲線參數。為了在有限域 Fp? 上實現 ECC，我們需要選擇一個素數 p 作為模數，并在該有限域上找到所有滿足橢圓曲線方程的整數點。這些點構成了橢圓曲線上的一個有限群，是 ECC 運算的基礎。通過遍歷 x 的所有可能值，計算對應的 y 值，并驗證其是否為二次剩余，可以準確地找到所有整數點。

2.橢圓曲線上的運算規則設計

在找到橢圓曲線上的所有點之后，需要設計橢圓曲線上的基本運算規則，這些規則是 ECC 的核心。主要包括：

點加法：定義了如何將兩個點 P 和 Q 相加，得到一個新的點 R。點加法的計算涉及到斜率的計算和新的坐標公式，需要考慮點是否相同、是否為無窮遠點等特殊情況。

點乘法：定義了如何將一個點 P 乘以一個標量 k，即計算 kP。點乘法可以通過重復的點加法實現，通常使用雙倍和加算法來提高效率。

點的逆元求解：定義了如何找到一個點 P 的逆元 ?P。在橢圓曲線上，點 P=(x,y) 的逆元是 ?P=(x,?y)，這在有限域中表示為 (x,p?y)。

3.加密與解密的實現

在主函數中，利用上述運算規則實現 ECC 的加密和解密過程。具體步驟如下：

密鑰生成：用戶輸入一個基點 G（生成元）和一個私鑰 d，計算公鑰 Q=dG。

加密：用戶輸入一個隨機數 k，計算 C1?=kG 和 C2?=M+kQ，其中 M 是明文點。

解密：使用私鑰 d 恢復明文點 M=C2??dC1?。

通過上述設計思路，ECC 能夠在較小的密鑰長度下提供高強度的安全性，同時保持高效的計算性能。這種設計不僅確保了加密和解密過程的正確性，還通過有限域上的運算特性提供了強大的安全性保障。

實驗結果如下：

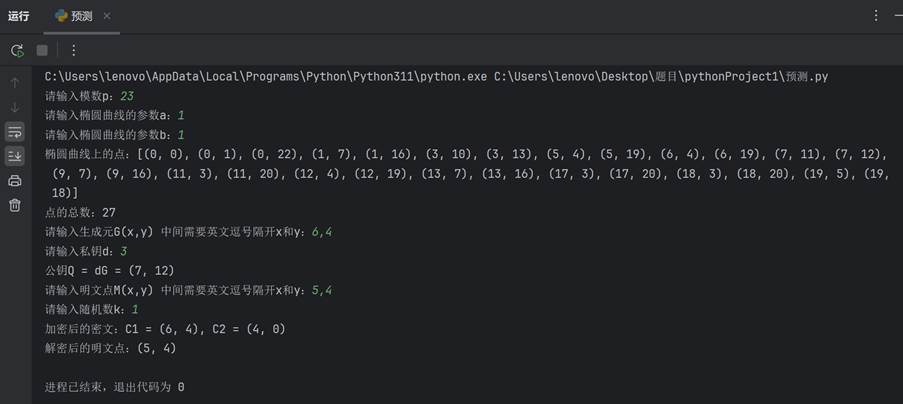
三、源代碼記錄（關鍵代碼需備注）

def findsolution(p, a, b):"""找到橢圓曲線 y^2 = x^3 + ax + b 在有限域 F_p 上的所有點"""s = []cnt = 0for i in range(p):z = (i**3 + a * i + b) % pif pow(z, (p - 1) // 2, p) == 1:y1 = pow(z, (p + 1) // 4, p)s.append((i, y1))cnt += 1y2 = p - y1if y1 != y2:s.append((i, y2))cnt += 1s.append((0, 0))  # 添加無窮遠點cnt += 1s.sort()return s, cntdef point_addition(p, a, P, Q):"""橢圓曲線上的點加法"""if P == (0, 0):return Qif Q == (0, 0):return Pif P == Q:if P[1] == 0:return (0, 0)  # 無窮遠點numerator = (3 * P[0]**2 + a) % pdenominator = (2 * P[1]) % pelse:if P[0] == Q[0] and P[1] != Q[1]:return (0, 0)  # 無窮遠點numerator = (Q[1] - P[1]) % pdenominator = (Q[0] - P[0]) % p# 計算斜率 lambdalambda_ = (numerator * pow(denominator, p - 2, p)) % p# 計算新的點x3 = (lambda_**2 - P[0] - Q[0]) % py3 = (lambda_ * (P[0] - x3) - P[1]) % preturn (x3, y3)def point_negation(p, P):"""計算點的逆點"""return (P[0], p - P[1])def point_multiplication(p, a, P, k):"""橢圓曲線上的點乘法"""result = (0, 0)temp = Pwhile k > 0:if k % 2 == 1:result = point_addition(p, a, result, temp)temp = point_addition(p, a, temp, temp)k //= 2return result# 輸入參數
p = int(input("請輸入模數p："))
a = int(input("請輸入橢圓曲線的參數a："))
b = int(input("請輸入橢圓曲線的參數b："))# 找到橢圓曲線上的所有點
points, point_count = findsolution(p, a, b)
print(f"橢圓曲線上的點：{points}")
print(f"點的總數：{point_count}")# 輸入生成元G和私鑰d
generator = tuple(map(int, input("請輸入生成元G(x,y) 中間需要英文逗號隔開x和y：").strip("()").split(",")))
private_key = int(input("請輸入私鑰d："))# 驗證生成元是否在橢圓曲線上
if generator not in points:raise ValueError("輸入的生成元G不在橢圓曲線上！")# 生成公鑰
public_key = point_multiplication(p, a, generator, private_key)
print(f"公鑰Q = dG = {public_key}")# 加密
plaintext_point = tuple(map(int, input("請輸入明文點M(x,y) 中間需要英文逗號隔開x和y：").strip("()").split(",")))
k = int(input("請輸入隨機數k："))  # 用于加密過程# 計算C1 = kG
C1 = point_multiplication(p, a, generator, k)
# 計算C2 = M + k * d * G
C2 = point_addition(p, a, plaintext_point, point_multiplication(p, a, generator, k * private_key))
print(f"加密后的密文：C1 = {C1}, C2 = {C2}")# 解密
# 計算M = C2 - k * d * G
decrypted_point = point_addition(p, a, C2, point_negation(p, point_multiplication(p, a, C1, private_key)))
print(f"解密后的明文點：{decrypted_point}")

四、實驗思考

ECC密碼算法的安全性在于什么？

答： ECC（橢圓曲線密碼學）的安全性主要基于橢圓曲線離散對數問題的計算困難性。

橢圓曲線離散對數問題（ECDLP）

ECC 的安全性依賴于橢圓曲線離散對數問題的計算難度。具體來說，給定橢圓曲線上的兩個點 P 和 Q，其中 Q=kP（k 是一個標量），在已知 P 和 Q 的情況下，計算標量 k 是非常困難的。這種計算困難性使得 ECC 在面對攻擊時具有很高的安全性。

計算難度：與傳統的離散對數問題（如在有限域中）相比，橢圓曲線上的離散對數問題被認為更加難以解決。目前，已知的最有效的算法（如 Pollard's rho 算法）在計算復雜度上仍然非常高，這使得 ECC 在較小的密鑰長度下就能提供與傳統加密算法（如 RSA）相當的安全性。

密鑰長度優勢：由于 ECDLP 的計算難度，ECC 可以使用較短的密鑰長度來實現相同的安全級別。例如，一個 256 位的 ECC 密鑰可以提供與 3072 位 RSA 密鑰相當的安全性。這使得 ECC 在計算資源有限的環境中（如移動設備和物聯網設備）具有顯著的優勢。