提示:100道LeetCode熱題-8-3主要是二叉樹相關,包括三題:將有序數組轉換為二叉搜索樹、驗證二叉搜索樹、二叉搜索樹中第K小的元素。由于初學,所以我的代碼部分僅供參考。
目錄
前言
題目1:將有序數組轉換為二叉搜索樹
1.題目要求:
2.結果代碼:
題目2:驗證二叉搜索樹
1.題目要求:
2.結果代碼:
題目3:二叉搜索樹中第K小的元素
1.題目要求:
2.結果代碼:
總結
前言
五一快樂~
二叉搜索樹奉上~
提示:以下是本篇文章正文內容,下面結果代碼僅供參考
題目1:將有序數組轉換為二叉搜索樹
1.題目要求:
題目如下:
給你一個整數數組?
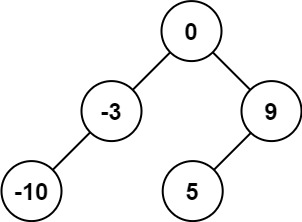
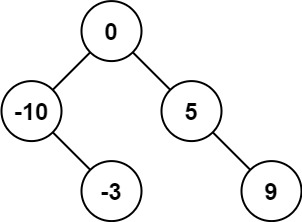
nums?,其中元素已經按?升序?排列,請你將其轉換為一棵?平衡?二叉搜索樹。示例 1:
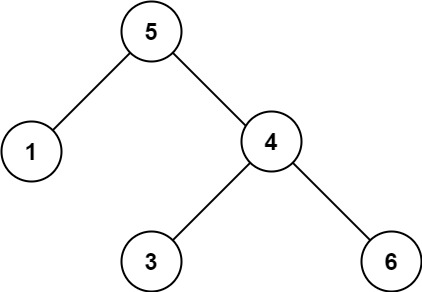
輸入:nums = [-10,-3,0,5,9] 輸出:[0,-3,9,-10,null,5] 解釋:[0,-10,5,null,-3,null,9] 也將被視為正確答案:
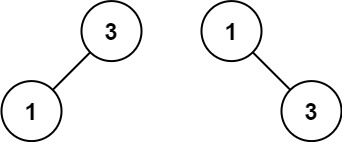
示例 2:
輸入:nums = [1,3] 輸出:[3,1] 解釋:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索樹。提示:
1 <= nums.length <=?-?<= nums[i] <=?
nums?按?嚴格遞增?順序排列
代碼框架已經提供如下:
# Definition for a binary tree node.
# class TreeNode(object):
# ? ? def __init__(self, val=0, left=None, right=None):
# ? ? ? ? self.val = val
# ? ? ? ? self.left = left
# ? ? ? ? self.right = right
class Solution(object):
? ? def sortedArrayToBST(self, nums):
? ? ? ? """
? ? ? ? :type nums: List[int]
? ? ? ? :rtype: Optional[TreeNode]
? ? ? ? """
? ? ? ?
2.結果代碼:
class Solution(object):def sortedArrayToBST(self, nums):if not nums:returnmid_index = len(nums) // 2return TreeNode(nums[mid_index], self.sortedArrayToBST(nums[:mid_index]), self.sortedArrayToBST(nums[mid_index + 1:]))說明:
1)更快,Python 的列表切片操作在底層是高度優化的,對于小數組,切片操作的常數開銷可能比遞歸調用的開銷小。

2)小心Python 的遞歸深度默認為 1000。如果數組非常大,遞歸調用可能會導致棧溢出。。
題目2:驗證二叉搜索樹
1.題目要求:
題目如下:
給你一個二叉樹的根節點?
root?,判斷其是否是一個有效的二叉搜索樹。有效?二叉搜索樹定義如下:
- 節點的左子樹只包含?小于?當前節點的數。
- 節點的右子樹只包含?大于?當前節點的數。
- 所有左子樹和右子樹自身必須也是二叉搜索樹。
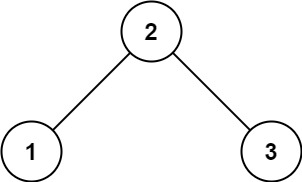
示例 1:
輸入:root = [2,1,3] 輸出:true示例 2:
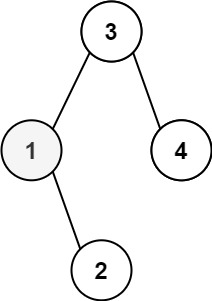
輸入:root = [5,1,4,null,null,3,6] 輸出:false 解釋:根節點的值是 5 ,但是右子節點的值是 4 。提示:
- 樹中節點數目范圍在
[1,?內]
-<= Node.val <=
- 1
代碼框架已經提供如下:
# Definition for a binary tree node.
# class TreeNode(object):
# ? ? def __init__(self, val=0, left=None, right=None):
# ? ? ? ? self.val = val
# ? ? ? ? self.left = left
# ? ? ? ? self.right = right
class Solution(object):
? ? def isValidBST(self, root):
? ? ? ? """
? ? ? ? :type root: Optional[TreeNode]
? ? ? ? :rtype: bool
? ? ? ? """
2.結果代碼:
方法一:遞歸檢查(帶范圍)
# Definition for a binary tree node.
class TreeNode(object):def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution(object):def isValidBST(self, root):""":type root: TreeNode:rtype: bool"""def is_valid_bst_helper(node, lower=float('-inf'), upper=float('inf')):if not node:return Trueif node.val <= lower or node.val >= upper:return Falsereturn (is_valid_bst_helper(node.left, lower, node.val) andis_valid_bst_helper(node.right, node.val, upper))return is_valid_bst_helper(root)-
定義了一個遞歸輔助函數
is_valid_bst_helper,它接收三個參數。 -
如果當前節點為空(
node為None),返回True,因為空樹是有效的二叉搜索樹。 -
如果當前節點的值小于等于下界或大于等于上界,返回
False,因為這違反了二叉搜索樹的性質。 -
遞歸檢查左右子樹:
-
對左子樹遞歸調用時,更新上界為當前節點的值(
node.val),因為左子樹的所有值必須小于當前節點的值。 -
對右子樹遞歸調用時,更新下界為當前節點的值,因為右子樹的所有值必須大于當前節點的值。
-
遞歸檢查左右子樹是否都滿足二叉搜索樹的性質。
-
方法二:中序遍歷
# Definition for a binary tree node.
class TreeNode(object):def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution(object):def isValidBST(self, root):""":type root: TreeNode:rtype: bool"""stack = []prev_val = float('-inf')curr = rootwhile curr or stack:while curr:stack.append(curr)curr = curr.leftcurr = stack.pop()if curr.val <= prev_val:return Falseprev_val = curr.valcurr = curr.rightreturn True-
使用一個棧來模擬遞歸的調用過程,初始化一個指針
curr指向根節點,prev_val用于記錄上一個訪問的節點值(初始為負無窮)。 -
遍歷過程:
-
沿著左子樹一直向下,將節點壓入棧中,直到左子樹為空。
-
彈出棧頂節點(即當前子樹的根節點),檢查其值是否大于
prev_val。 -
如果當前節點的值小于等于
prev_val,返回False,因為這違反了二叉搜索樹的性質。 -
更新
prev_val為當前節點的值,然后將指針移動到右子樹。
-
題目3:二叉搜索樹中第K小的元素
1.題目要求:
題目如下:
給定一個二叉搜索樹的根節點?
root?,和一個整數?k?,請你設計一個算法查找其中第?k?小的元素(從 1 開始計數)。示例 1:
輸入:root = [3,1,4,null,2], k = 1 輸出:1示例 2:
輸入:root = [5,3,6,2,4,null,null,1], k = 3 輸出:3提示:
- 樹中的節點數為?
n?。1 <= k <= n <=?0 <= Node.val <=?進階:如果二叉搜索樹經常被修改(插入/刪除操作)并且你需要頻繁地查找第?
k?小的值,你將如何優化算法?
代碼框架已經提供如下:
# Definition for a binary tree node.
# class TreeNode(object):
# ? ? def __init__(self, val=0, left=None, right=None):
# ? ? ? ? self.val = val
# ? ? ? ? self.left = left
# ? ? ? ? self.right = right
class Solution(object):
? ? def kthSmallest(self, root, k):
? ? ? ? """
? ? ? ? :type root: Optional[TreeNode]
? ? ? ? :type k: int
? ? ? ? :rtype: int
? ? ? ? """
2.結果代碼:
class Solution:def kthSmallest(self, root, k):stack = []curr = rootcount = 0while curr or stack:while curr:stack.append(curr)curr = curr.leftcurr = stack.pop()count += 1if count == k:return curr.valcurr = curr.right說明:使用棧模擬遞歸過程,避免遞歸調用的開銷。
邏輯:
-
使用棧存儲節點,模擬遞歸的中序遍歷。
-
先將當前節點的所有左子節點壓入棧中。
-
彈出棧頂節點,計數加 1,檢查是否為第 k 個節點。
-
如果未達到第 k 個節點,繼續遍歷右子樹。
進階優化:如果二叉搜索樹經常被修改(插入/刪除操作),并且需要頻繁查找第 k 小的值,可以采用以下優化方法:
-
存儲子樹大小:在每個節點中增加一個字段,記錄其左子樹的節點數量。這樣可以在遍歷時快速跳過不必要的子樹。
-
高效查找:通過子樹大小信息,直接定位到第 k 小的節點,而無需完整遍歷。
這種方法的時間復雜度為 O(h),其中 h 是樹的高度,對于平衡二叉搜索樹,復雜度為 O(log n)。
總結
針對二叉樹的三種題型進行了學習,了解了部分有關二叉樹與python的相關知識,大家加油!

)

:C 語言函數可變參數詳解)
Nova Cell理解)








)

)




