數據結構初階：二叉樹（四）

概述：本篇博客主要介紹鏈式結構二叉樹的實現。

1.實現鏈式結構二叉樹

1.1 二叉樹的頭文件（tree.h）

1.2 創建二叉樹?

?1.3 前中后序遍歷

1.3.1 遍歷規則?

1.3.1.1 前序遍歷代碼實現

1.3.1.2??中序遍歷代碼實現

1.3.1.3? 后序遍歷代碼實現

?1.4 二叉樹結點的個數

?1.5 二叉樹葉子結點個數

1.6? 二叉樹第k層結點個數

1.7? 二叉樹的深度/高度

?編輯

?1.8 查找值為x的結點

1.9 二叉樹的銷毀?

2. 小結?

1.實現鏈式結構二叉樹

1.1 二叉樹的頭文件（tree.h）

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>//定義鏈式結構二叉樹
//二叉樹結點的結構
typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//前序遍歷
void preOrder(BTNode* root);
//中序遍歷
void InOrder(BTNode* root);
//后序遍歷
void postOrder(BTNode* root);//二叉樹結點個數
int BinaryTreeSize(BTNode* root);
//void BinaryTreeSize(BTNode* root,int* psize);//二叉樹葉子結點個數
int BinaryTreeLeafSize(BTNode* root);//二叉樹第k層結點個數
int BinaryTreeLevelKSize(BTNode* root, int k);//二叉樹的深度/高度
int BinaryTreeDepth(BTNode* root);//二叉樹查找值為x的結點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);//二叉樹銷毀
void BinaryTreeDestroy(BTNode** root);//層序遍歷
void LevelOrder(BTNode* root);//判斷二叉樹是否是完全二叉樹
bool BinaryTreeComplete(BTNode* root);

1.2 創建二叉樹?

?用鏈表來表示一顆二叉樹，即用鏈來指示元素的邏輯關系。通常的方法是鏈表中每個結點由三個域組成，數據域和左右指針域，左右指針分別用來給出該結點左孩子和右孩子所在的鏈結點的存儲地址，其結構如下：

//定義鏈式結構二叉樹
//二叉樹結點的結構
typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;  // 指向當前結點左孩子struct BinaryTreeNode* right; // 指向當前結點右孩子
}BTNode;

二叉樹的創建方式比較復雜，為了更好走進二叉樹的學習中，我們先手動構建一顆鏈式二叉樹。?

#include"Tree.h"
BTNode* buyNode(char x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));node->data = x;node->left = node->right = NULL;return node;
}
BTNode* creatBinaryTree()
{BTNode* nodeA = buyNode('A');BTNode* nodeB = buyNode('B');BTNode* nodeC = buyNode('C');BTNode* nodeD = buyNode('D');BTNode* nodeE = buyNode('E');BTNode* nodeF = buyNode('F');nodeA->left = nodeB;nodeA->right = nodeC;nodeB->left = nodeD;nodeC->left = nodeE;nodeC->right = nodeF;return nodeA;
}

回顧二叉樹的概念，二叉樹分為空樹和非空二叉樹，非空二叉樹由根結點根結點的左子樹、根結點的右子樹組成的。?

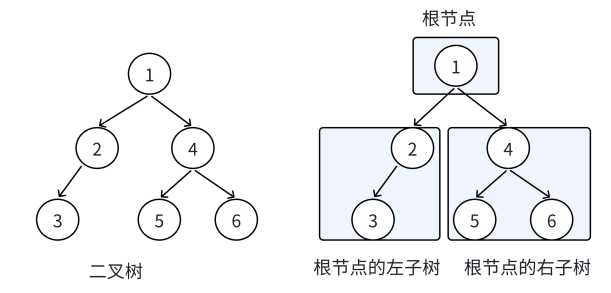
?根結點的左子樹和右子樹分別又是由子樹結點、子樹結點的左子樹、子樹結點的右子樹組成的，因此二叉樹定義式遞歸式的，后續鏈式二叉樹的操作基本都是按照該概念實現的。

?1.3 前中后序遍歷

二叉樹的操作離不開樹的遍歷，我們先來看一下二叉樹的遍歷有哪些方式。?

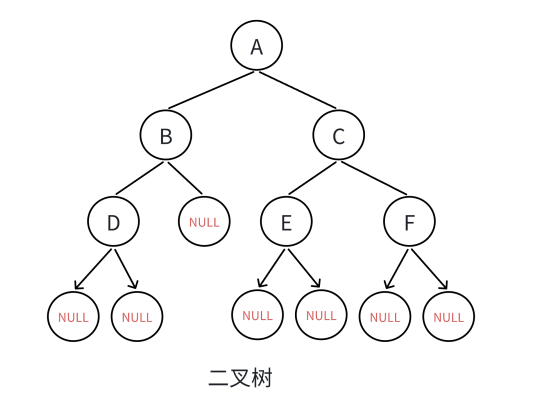
1.3.1 遍歷規則?

?按照規則，二叉樹的遍歷有：前序/中序/后序的遞歸結構遍歷：

1）前序遍歷(Preorder Traversal 亦稱先序遍歷)：訪問根結點的操作發生在遍歷其左右子樹之前

訪問順序為：根結點、左子樹、右子樹

?2）中序遍歷(Inorder Traversal)：訪問根結點的操作發?在遍歷其左右子樹之中（間）

訪問順序為：左子樹、根結點、右子樹?

3）后序遍歷(Postorder Traversal)：訪問根結點的操作發生在遍歷其左右子樹之后

?訪問順序為：左子樹、右子樹、根結點

1.3.1.1 前序遍歷代碼實現

void preOrder(BTNode* root)
{if(root == NULL){printf("NULL ");return;}printf("%c ", root->data);preOrder(root->left);preOrder(root->right);
}

邏輯概述：?

?這段代碼定義了一個先序遍歷二叉樹的函數 `preOrder`。函數的參數是一個指向二叉樹節點的指針 `root`。

如果 `root` 為空，函數會輸出 `NULL` 并返回。否則，函數會先輸出當前節點的數據，然后對左子樹和右子樹分別遞歸調用 `preOrder` 函數進行先序遍歷。

在代碼中，`printf("%c ", root->data);` 用于輸出當前節點的數據，假設 `data` 是字符類型。?

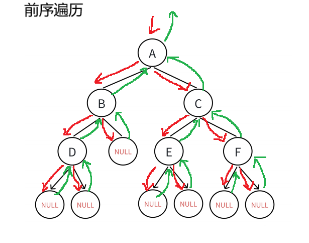
1.3.1.2??中序遍歷代碼實現

void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}

邏輯概述：?

這段代碼是一個二叉樹的中序遍歷函數。其功能是：如果根節點為空，輸出"NULL "并返回；否則，先對左子樹進行中序遍歷，然后輸出根節點的數據，最后對右子樹進行中序遍歷。其實現過程與常見的二叉樹中序遍歷的邏輯一致。?

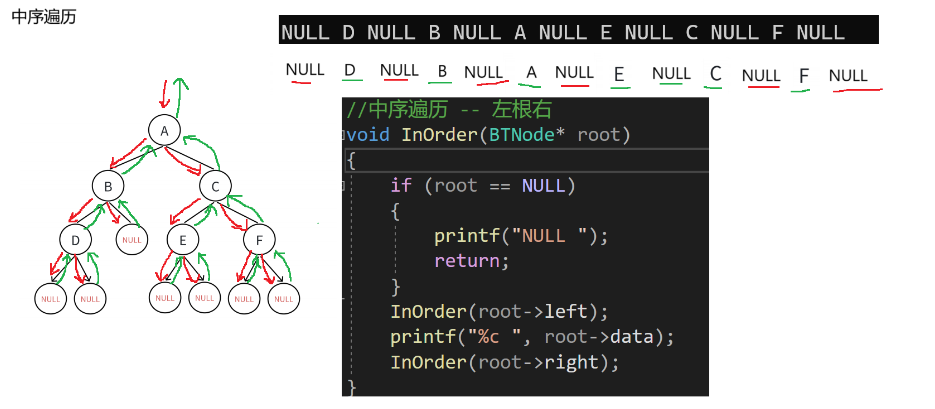
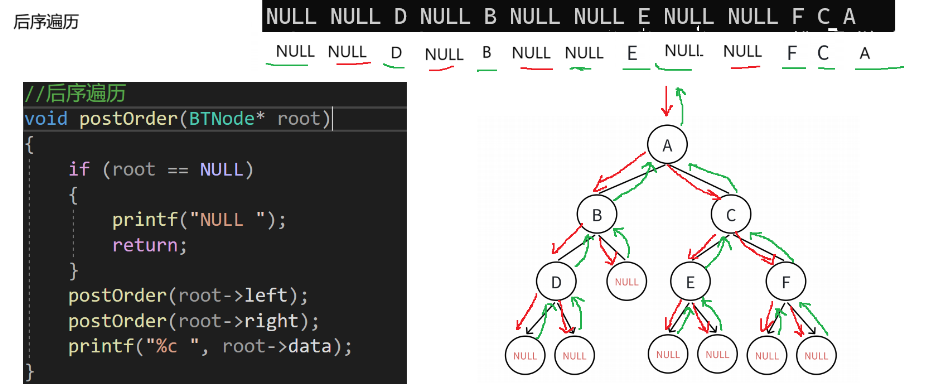
1.3.1.3? 后序遍歷代碼實現

void postOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}postOrder(root->left);postOrder(root->right);printf("%c ", root->data);
}

邏輯概述：?

?這段代碼定義了一個二叉樹的后序遍歷函數 `postOrder` 。函數的作用是：如果根節點為空，輸出 `"NULL "` 并返回；否則，先對左子樹進行后序遍歷，再對右子樹進行后序遍歷，最后輸出根節點的數據。這符合二叉樹后序遍歷的邏輯，即先遍歷左子樹，再遍歷右子樹，最后訪問根節點。?

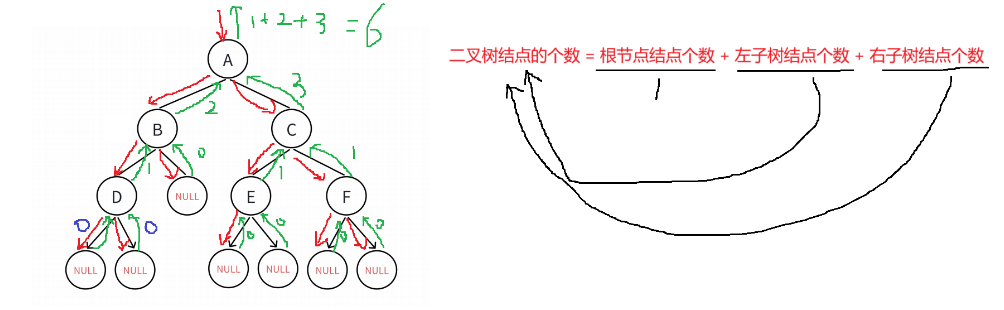
?1.4 二叉樹結點的個數

int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return 1 + BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

邏輯概述：?

?這段代碼定義了一個計算二叉樹節點個數的函數 `BinaryTreeSize` 。

函數的邏輯是：如果根節點為空，返回 0；如果根節點的左右子樹都為空，返回 1；否則，返回 1 加上左子樹的節點個數和右子樹的節點個數。其中，左子樹和右子樹的節點個數通過遞歸調用 `BinaryTreeLeafSize` 函數來計算。?

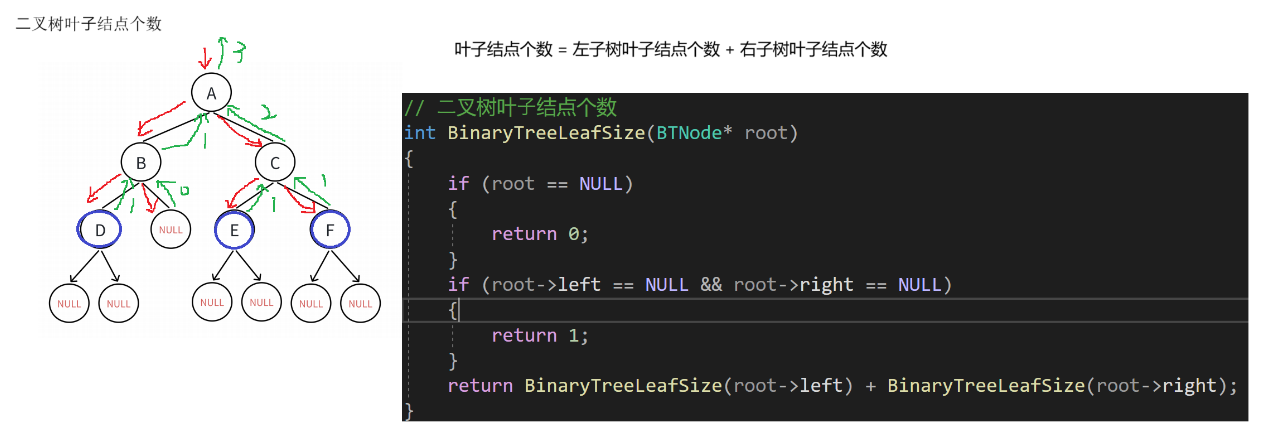
?1.5 二叉樹葉子結點個數

//二叉樹葉子結點個數
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

?邏輯概述：

?這段代碼定義了一個計算二叉樹葉子結點個數的函數`BinaryTreeLeafSize`。

函數的邏輯是：如果根節點為空，返回0；如果根節點的左右子樹都為空，說明該節點為葉子節點，返回1；否則，通過遞歸調用函數本身，分別計算左子樹和右子樹的葉子節點個數，并將它們相加后返回。?

1.6? 二叉樹第k層結點個數

// 計算二叉樹第 k 層結點個數
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL) {return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

?邏輯概述：

這段代碼的功能是計算二叉樹中第k層的節點個數。如果根節點為空，返回0。如果k等于1，說明當前根節點就是第k層的節點，返回1。否則，通過遞歸調用函數本身，分別計算左子樹和右子樹中第k - 1層的節點個數，并將它們相加后返回。

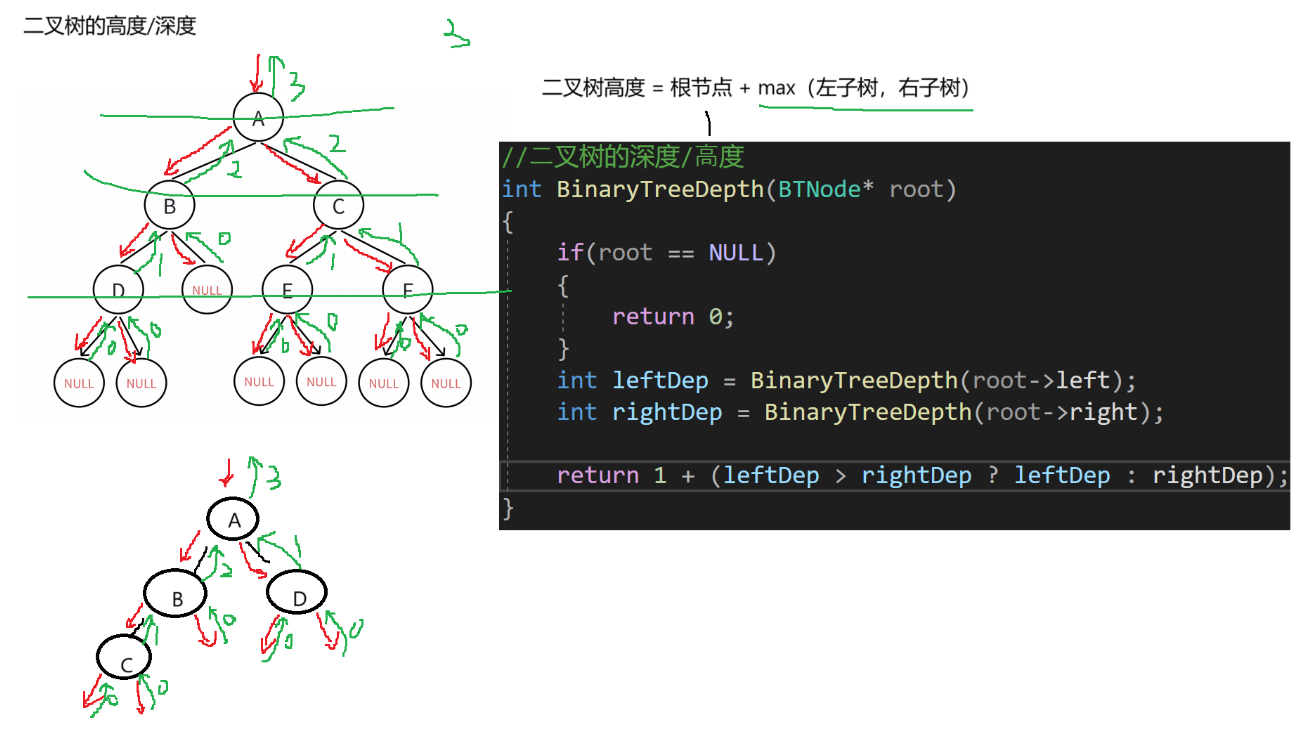
1.7? 二叉樹的深度/高度

//二叉樹的深度/高度
int BinaryTreeDepth(BTNode* root)
{if (root == NULL){return 0;}int leftDep = BinaryTreeDepth(root->left);int rightDep = BinaryTreeDepth(root->right);return 1 + (leftDep > rightDep ? leftDep : rightDep);
}

邏輯概述：?

?這段代碼定義了一個計算二叉樹深度（高度）的函數 `BinaryTreeDepth` 。

函數的邏輯是：如果根節點為空，返回 0 。然后分別計算左子樹和右子樹的深度，記為 `leftDep` 和 `rightDep` 。最后，二叉樹的深度為 1 加上 `leftDep` 和 `rightDep` 中的較大值。?

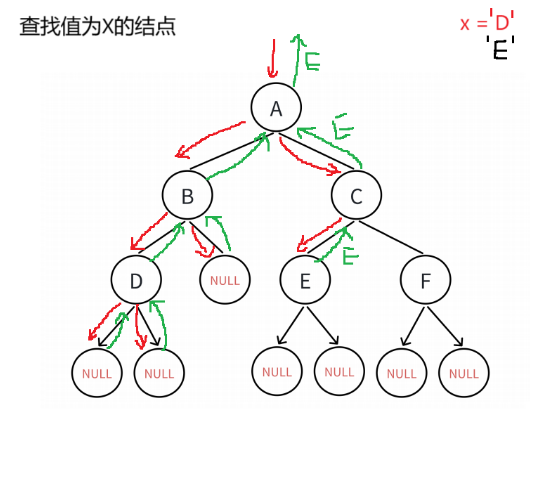
?1.8 查找值為x的結點

//二叉樹查找值為x的結點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* leftFind = BinaryTreeFind(root->left, x);if (leftFind){return leftFind;}BTNode* rightFind = BinaryTreeFind(root->right, x);if (rightFind){return rightFind;}return NULL;
}

邏輯概述：?

?這段代碼定義了一個在二叉樹中查找值為`x`的節點的函數`BinaryTreeFind`。

函數的執行過程如下：
- 如果根節點為空，直接返回`NULL`，表示未找到。
- 如果根節點的值等于`x`，則返回根節點。
- 然后在左子樹中遞歸查找值為`x`的節點，如果找到則返回該節點。
- 如果在左子樹中未找到，再在右子樹中遞歸查找值為`x`的節點，如果找到則返回該節點。
- 如果在整個二叉樹中都未找到值為`x`的節點，則最終返回`NULL`。?

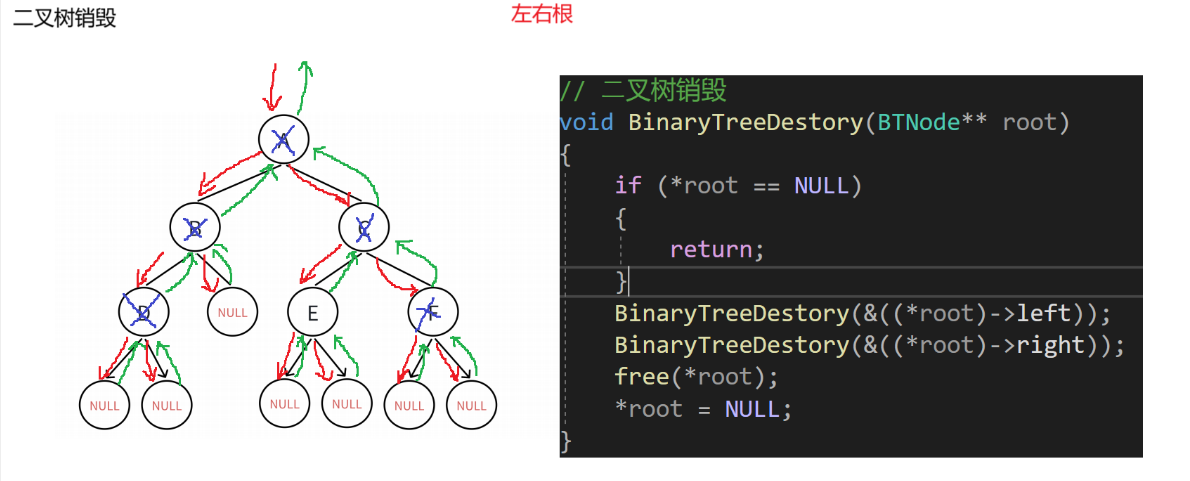
1.9 二叉樹的銷毀?

//二叉樹銷毀
void BinaryTreeDestroy(BTNode** root)
{if (*root == NULL){return;}BinaryTreeDestroy(&((*root)->left));BinaryTreeDestroy(&((*root)->right));*root == NULL;
}