一、紅黑樹
1、紅黑樹
? ? 前面介紹了2-3樹,可以看到2-3樹能保證在插入元素之后,樹依然保持平衡狀態,它的最壞情況下所有子結點都是2-結點,樹的高度為IgN,相比于我們普通的二叉查找樹,最壞情況下樹的高度為N,確實保證了最壞情況下的時間復雜度,但是2-3樹實現起來過于復雜,所以我們介紹一種2-3樹思想的簡單實現:紅黑樹。
? ? 紅黑樹主要是對2-3樹進行編碼,紅黑樹背后的基本思想是用標準的二叉查找樹(完全由2-結點構成)和一些額外的信息(替換3-結點)來表示2-3樹。我們將樹中的鏈接分為兩種類型:
? ? ? ? 紅鏈接:將兩個2-結點連接起來構成一個3-結點,
? ? ? ? 黑鏈接:則是2-3樹中的普通鏈接。
? ? 確切的說,我們將3-結點表示為由由一條左斜的紅色鏈接(兩個2-結點其中之一是另一個的左子結點)相連的兩個2-結點。這種表示法的個優點是,我們無需修改就可以直接使用標準的二叉查找樹的get方法。
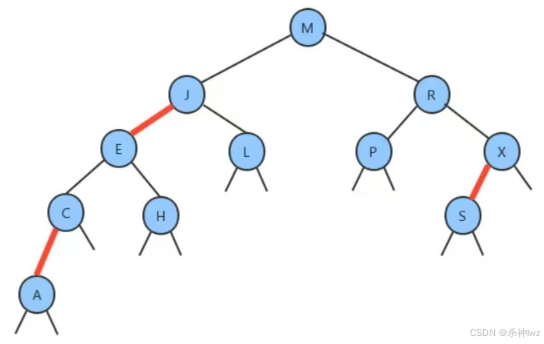
1.1、紅黑樹的定義
紅黑樹是含有紅黑鏈接并滿足下列條件的二叉查找樹:
? ? 1、紅鏈接均為左鏈接;
? ? 2、沒有任何一個結點同時和兩條紅鏈接相連;
? ? 3、該樹是完美黑色平衡的,即任意空鏈接到根結點的路徑上的黑鏈接數量相同;
下面是紅黑樹與2-3樹的對應關系:



1.2、紅黑樹結點API
? ? 因為每個結點都只會有一條指向自己的鏈接(從它的父結點指向它),我們可以在之前的Node結點中添加一個布爾類型的變量color來表示鏈接的顏色。如果指向它的鏈接是紅色的,那么該變量的值為true,如果鏈接是黑色的,那么該變量的值為false。

API設計:
| 類名 | Node<Key,Value> |
| 構造方法 | Node(Key key, Value value, Node left, Node right , boolean color):創建Node對象 |
| 成員變量 | 1.public Node left:記錄左子結點 2.public Node right:記錄右子結點 3.public Key key:存儲鍵 4.public Value value:存儲值 5.public boolean color:由其結點指向它的鏈接的顏色 |
代碼:
public class Node<Key, Value> {//存儲鍵public key key;//存儲值private value value;//記錄左子結點public Node left;//記錄右子結點public Node right;//由其父結點指向它的鏈接的顏色public boolean color;public Node(Key key, Value value, Node left, Node right, boolean color) {this.key = key;this.value = value;this.left = left;this.right = right;this.color = color;}
}1.3、平衡化
? ? 在對紅黑樹進行一些增刪改查的操作后,很有可能會出現紅色的右鏈接或者兩條連續紅色的鏈接,而這些都不滿足紅黑樹的定義,所以我們需要對這些情況通過旋轉進行修復,讓紅黑樹保持平衡。
1.3.1、左旋
? ? 當某個結點的左子結點為黑色,右子結點為紅色,此時需要左旋。
前提:當前結點為h,它的右子結點為x;
左旋過程:
? ? 1、讓x的左子結點變為h的右子結點:h.right=x.left;
? ? 2、讓h成為x的左子結點:x.left=h;
? ? 3、讓h的color屬性變為x的color屬性值:x.color=h.color;
? ? 4、讓h的color屬性變為RED:h.color=true;


1.3.2、右旋
? ? 當某個結點的左子結點是紅色,且左子結點的左子結點也是紅色,需要右旋。
前提:當煎結點為h,它的左子結點為x;
右旋過程:
? ? 1、讓x的右子結點成為h的左子結點:h.left=x.right;
? ? 2、讓h成為x的右子結點:x.right=h;
? ? 3、讓x的color變為h的color屬性值:x.color =h.color;
? ? 4、讓h的color為RED ;


數據結構和算法(一)
數據結構和算法(八)--2-3查找樹
數據結構--棧、隊列、鏈表、散列表、排序二叉樹
再小的努力,乘以365都很明顯!
每天??記錄?點點。內容也許不重要,但習慣很重要!
一個程序員最重要的能力是:寫出高質量的代碼!!
有道無術,術尚可求也,有術無道,止于術。
無論你是年輕還是年長,所有程序員都需要記住:時刻努力學習新技術,否則就會被時代拋棄!



















