LeetCode 熱題 100：回溯

46. 全排列

給定一個不含重復數字的數組 nums ，返回其 所有可能的全排列 。你可以 按任意順序 返回答案。

示例 1：
輸入：nums = [1,2,3]
輸出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：
輸入：nums = [0,1]
輸出：[[0,1],[1,0]]
示例 3：
輸入：nums = [1]
輸出：[[1]]
提示：

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整數 互不相同

vector<vector<int>> ans;
vector<int> path;
vector<bool> vis;vector<vector<int>> permute(vector<int>& nums) {int n = nums.size();vis = vector<bool>(n, false);dfs(nums);return ans;
}void dfs(vector<int>& nums) {int n = nums.size();if (path.size() == n) {ans.push_back(path);return;}for (int i = 0; i < n; ++i) {if (vis[i] == false) {path.push_back(nums[i]);vis[i] = true;dfs(nums);path.pop_back();vis[i] = false;}}
}

78. 子集

給你一個整數數組 nums ，數組中的元素 互不相同 。返回該數組所有可能的子集（冪集）。

解集不能包含重復的子集。你可以按 任意順序 返回解集。

示例 1：
輸入：nums = [1,2,3]
輸出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2：
輸入：nums = [0]
輸出：[[],[0]]
提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

vector<vector<int>> ans;
vector<int> path;vector<vector<int>> subsets(vector<int>& nums) {dfs(nums, 0);return ans;
}void dfs(vector<int>& nums, int pos) {if (pos == nums.size()) {ans.push_back(path);return;}dfs(nums, pos + 1);path.push_back(nums[pos]);dfs(nums, pos + 1);path.pop_back();
}

另一種方法

vector<vector<int>> ans;
vector<int> path;vector<vector<int>> subsets(vector<int>& nums) {dfs(nums, 0);return ans;
}void dfs(vector<int>& nums, int pos) {ans.push_back(path);for (int i = pos; i < nums.size(); ++i) {path.push_back(nums[i]);dfs(nums, i + 1);path.pop_back();}
}

17. 電話號碼的字母組合

給定一個僅包含數字 2-9 的字符串，返回所有它能表示的字母組合。答案可以按 任意順序 返回。

給出數字到字母的映射如下（與電話按鍵相同）。注意 1 不對應任何字母。

示例 1：
輸入：digits = "23"
輸出：["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2：
輸入：digits = ""
輸出：[]
示例 3：
輸入：digits = "2"
輸出：["a","b","c"]
提示：

0 <= digits.length <= 4
digits[i] 是范圍 ['2', '9'] 的一個數字。

vector<string> ans;
string path;
vector<string> nums = {"", "", "abc", "def","ghi", "jkl", "mno","pqrs", "tuv", "wxyz"
};vector<string> letterCombinations(string digits) {if (digits.size() == 0) {return ans;}dfs(digits, 0);return ans;
}void dfs(string digits, int pos) {if (path.size() == digits.size()) {ans.push_back(path);return;}int n = digits[pos] - '0';string str = nums[n];for (int i = 0; i < str.size(); ++i) {path.push_back(str[i]);dfs(digits, pos + 1);path.pop_back();}
}

39. 組合總和

給你一個 無重復元素 的整數數組 candidates 和一個目標整數 target ，找出 candidates 中可以使數字和為目標數 target 的所有 不同組合 ，并以列表形式返回。你可以按 任意順序 返回這些組合。

candidates 中的 同一個 數字可以 無限制重復被選取 。如果至少一個數字的被選數量不同，則兩種組合是不同的。

對于給定的輸入，保證和為 target 的不同組合數少于 150 個。

示例 1：
輸入：candidates = [2,3,6,7], target = 7
輸出：[[2,2,3],[7]]
解釋：
2 和 3 可以形成一組候選，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一個候選， 7 = 7 。
僅有這兩種組合。
示例 2：
輸入: candidates = [2,3,5], target = 8
輸出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3：
輸入: candidates = [2], target = 1
輸出: []
提示：

1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40

vector<vector<int>> ans;
vector<int> path;vector<vector<int>> combinationSum(vector<int>& candidates, int target) {dfs(candidates, target, 0, 0);return ans;
}void dfs(vector<int>& candidates, int target, int sum, int pos) {if (sum > target) {return;}if (sum == target) {ans.push_back(path);return;}for (int i = pos; i < candidates.size(); ++i) {path.push_back(candidates[i]);dfs(candidates, target, sum + candidates[i], i);path.pop_back();}
}

22. 括號生成

數字 n 代表生成括號的對數，請你設計一個函數，用于能夠生成所有可能的并且 有效的 括號組合。

示例 1：
輸入：n = 3
輸出：["((()))","(()())","(())()","()(())","()()()"]
示例 2：
輸入：n = 1
輸出：["()"]
提示：

1 <= n <= 8

vector<string> ans;
string path;vector<string> generateParenthesis(int n) {dfs(n, 0, 0);return ans;
}void dfs(int n, int left, int right) {if (left + right == 2 * n) {ans.push_back(path);return;}if (left < n) {path.push_back('(');dfs(n, left + 1, right);path.pop_back();}if (right < left) {path.push_back(')');dfs(n, left, right + 1);path.pop_back();}
}

79. 單詞搜索

給定一個 m x n 二維字符網格 board 和一個字符串單詞 word 。如果 word 存在于網格中，返回 true ；否則，返回 false 。

單詞必須按照字母順序，通過相鄰的單元格內的字母構成，其中“相鄰”單元格是那些水平相鄰或垂直相鄰的單元格。同一個單元格內的字母不允許被重復使用。

示例 1：
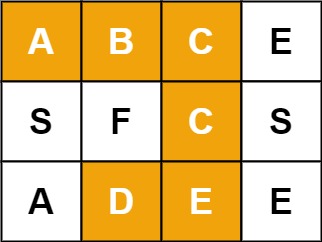
輸入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
輸出：true
示例 2：
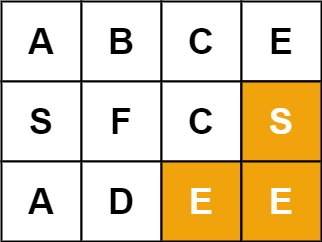
輸入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
輸出：true
示例 3：
輸入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
輸出：false
提示：

m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 僅由大小寫英文字母組成

vector<vector<bool>> vis;
const int dx[4] = {0, 0, 1, -1};
const int dy[4] = {1, -1, 0, 0};bool exist(vector<vector<char>>& board, string word) {int n = board.size(), m = board[0].size();vis = vector<vector<bool>>(n, vector<bool>(m, false));for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (board[i][j] == word[0]) {vis[i][j] = true;if (dfs(board, word, i, j, 1) == true) {return true;}vis[i][j] = false;}}}return false;
}bool dfs(vector<vector<char>>& board, const string& word, int x, int y, int pos) {if (pos == word.size()) {return true;}int n = board.size(), m = board[0].size();for (int k = 0; k < 4; ++k) {int nx = x + dx[k], ny = y + dy[k];if (nx >= 0 && nx < n && ny >= 0 && ny < m && board[nx][ny] == word[pos] && vis[nx][ny] == false) {vis[nx][ny] = true;if (dfs(board, word, nx, ny, pos + 1) == true) {return true;}vis[nx][ny] = false;}}return false;
}

131. 分割回文串

給你一個字符串 s，請你將 s 分割成一些子串，使每個子串都是 回文串 。返回 s 所有可能的分割方案。

示例 1：
輸入：s = "aab"
輸出：[["a","a","b"],["aa","b"]]
示例 2：
輸入：s = "a"
輸出：[["a"]]
提示：

1 <= s.length <= 16
s 僅由小寫英文字母組成

vector<vector<string>> ans;
vector<string> path;
unordered_set<string> hash;
unordered_set<string> nonhash;vector<vector<string>> partition(string s) {dfs(s, 0);return ans;
}void dfs(const string& s, int pos) {if (pos == s.size()) {ans.push_back(path);return;}// pos開始，i結尾for (int i = pos; i < s.size(); ++i) {string str = s.substr(pos, i - pos + 1);if (isPalindrome(str)) {path.push_back(str);dfs(s, i + 1);path.pop_back();}}
}bool isPalindrome(const string& s) {if (hash.count(s)) {return true;}if (nonhash.count(s)) {return false;}int left = 0, right = s.size() - 1;while (left < right) {if (s[left] != s[right]) {nonhash.insert(s);return false;}left++, right--;}hash.insert(s);return true;
}

51. N 皇后

按照國際象棋的規則，皇后可以攻擊與之處在同一行或同一列或同一斜線上的棋子。

n 皇后問題 研究的是如何將 n 個皇后放置在 n×n 的棋盤上，并且使皇后彼此之間不能相互攻擊。

給你一個整數 n ，返回所有不同的 n 皇后問題 的解決方案。

每一種解法包含一個不同的 n 皇后問題 的棋子放置方案，該方案中 'Q' 和 '.' 分別代表了皇后和空位。

示例 1：
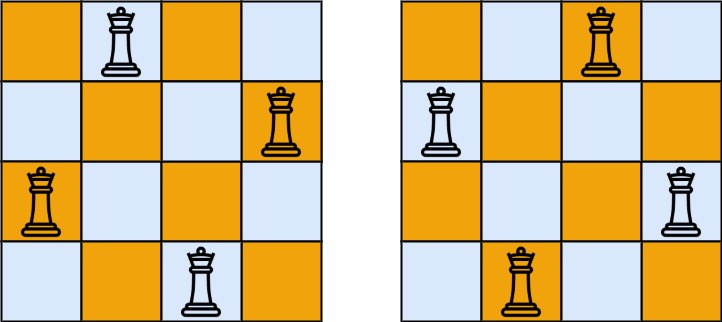
輸入：n = 4
輸出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解釋：如上圖所示，4 皇后問題存在兩個不同的解法。
示例 2：
輸入：n = 1
輸出：[["Q"]]
提示：

1 <= n <= 9

通過x = 0時y = b來判斷是否當前斜線上有無皇后。

vector<vector<string>> ans;
vector<string> path;
bool vis[10];
bool vis1[20]; // y - x = b
bool vis2[20]; // y + x = bvector<vector<string>> solveNQueens(int n) {path.resize(n);for (int i = 0; i < n; ++i) {path[i].append(n, '.');}dfs(n, 0);return ans;
}void dfs(int n, int y) {if (y == n) {ans.push_back(path);return;}for (int x = 0; x < n; ++x) {if (!vis[x] && !vis1[y - x + 10] && !vis2[y + x]) {path[y][x] = 'Q';vis[x] = vis1[y - x + 10] = vis2[y + x] = true;dfs(n, y + 1);path[y][x] = '.';vis[x] = vis1[y - x + 10] = vis2[y + x] = false;}}
}