? ? ? ? 我之前只看到了數據結構與算法的冰山一角，感覺這些術語只會讓知識越來越難理解，現在來看，他們完美抽象一些概念和知識，非常重要。

????????本篇概念肯定總結不全，只有遇到的會寫上，持續更新，之前文章已經提過的如并查集、最短路徑、鄰接表等不再重復，這里為補充。

---

????????圖形結構中的元素之間存在多對多的聯系。

? ? ? ? 圖形結構中，每一個元素前驅結點可以有多個，后繼結點也可以有多個。? ??

?????????首先我們肯定都知道圖可以分為有向圖和無向圖，它們各自有一些獨屬于自己的術語和共同的術語，下面這個思維導圖幫大家理清一些概念：??

---

共同術語?

我們先從共同的概念說起 ：

• 完全圖：針對有向圖和無向圖，即每兩個頂點都有一條邊（有向圖至少??條邊，無向圖至少條邊），如圖所示。

• 稀疏圖與稠密圖?：根據概念來說，有很少條邊或弧（如??，其中e為邊的數目，n為頂點的個數）。需要注意的的是，因為這兩個概念常用于選擇鄰接矩陣或鄰接表，具體選用要與算法結合。
• 權和網：權和網可以理解為帶權圖，在絕大數應用中，每條邊應該是帶有權重的，權可以表示從一個頂點到另一個頂點的距離、時間或代價等含義。
• 鄰接點：無向圖中鄰接點是沒有方向的，或者稱為對稱的，假若頂點v 和頂點w 之間存在一條邊， 則稱頂點v 和w 互為鄰接點。在有向圖中，鄰接點是有方向的，如果存在從頂點到頂點的有向邊，那么我們說頂點是頂點的出邊鄰接點，頂點是頂點的入邊鄰接點。

無向圖

• 連通：兩個頂點有路徑。
• 連通圖：任意兩個頂點有路徑，但不一定都有邊。
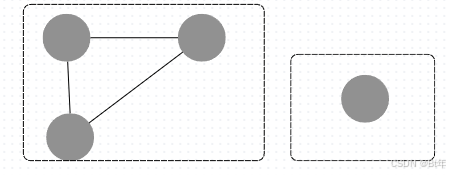
• 連通分量：指在無向圖中的極大連通子圖，如圖中的無向非連通圖有兩個連通分量。

• 度：頂點v的度是指和v相關聯的邊的數目；如圖中，頂點v的度為3。

有向圖

• 強連通圖：任意兩個頂點有路徑，但不一定都有邊。（注意并不一定兩個頂點和有兩條邊，只要可以形成環就行。）完全有向圖肯定就是強連通圖。
• 強連通分量：有向圖中的極大強連通子圖稱作有向圖的強連通分量，如圖所示的有向非強連通圖有兩個強連通分量。

• 出度和入度：對于有向圖，頂點v的度被分為出度和入度，入度是以頂點v為頭的的弧數目（箭頭指向v），出度就是以頂點v為尾的的弧數目。頂點v的入度為1，出度為2。?

壓縮存儲

????????壓縮存儲是指在不丟失數據信息的前提下，對數據進行重新編碼或組織，以減少數據所占用的存儲空間的方法。通過特定的算法和數據結構，將原始數據轉換為一種更緊湊的表示形式，在需要使用數據時再進行解壓縮還原。

? ? ? ? 這里主要介紹矩陣的壓縮存儲。

? ? ? ? 對稱矩陣

? ? ? ? 即，首先我們先回顧一個等差數列的公式：。

根據這個公式，我們就可以把一個n維矩陣，用一個一維數組進行存儲了。無向圖的鄰接矩陣就是對稱矩陣可用一維數組壓縮儲存。?

? ? ? ? 可以按行主序即下三角存儲；或者按列主序即上三角存儲。如果我們要找矩陣中位置第i行第j列的元素,還是利用上面等差數列公式按行存儲和列存儲即可搞定。

? ? ? ? 三角矩陣

? ? ? ? 三角矩陣即只有矩陣的一個三角的數字有意義，對稱矩陣就可以理解為三角矩陣，所以三角矩陣的壓縮儲存與對角矩陣基本一樣。

? ? ? ? 對角矩陣

? ? ? ? 就是只在對角線上存在的元素有意義。 一般分兩種方式存儲：行序存儲和對角線。

????????可以將主對角線元素存儲在一個一維數組中，通過數組下標與矩陣主對角線元素的對應關系來實現對矩陣元素的訪問和操作。例如，對于對角矩陣的主對角線元素，可以存儲在一維數組中，。

? ? ? ? 其它

? ? ? ? 另外稀疏矩陣的壓縮存儲可以用一個三元組表來表示稀疏矩陣中的非0元素。

????????稀疏矩陣是指矩陣中絕大多數元素為 0，只有少數非 0 元素的矩陣。為了節省存儲空間和提高運算效率，通常采用壓縮存儲的方式來存儲稀疏矩陣，其中一種常見的方法就是用三元組表來表示稀疏矩陣中的非 0 元素。

????????三元組表中的每個三元組通常表示為（行標，列標，值），分別記錄了稀疏矩陣中每個非 0 元素所在的行、列位置以及該元素的值。通過這種方式，可以只存儲稀疏矩陣中的非 0 元素，而不必像常規的二維數組存儲方式那樣為大量的 0 元素分配存儲空間，從而達到壓縮存儲的目的。例如，對于一個稀疏矩陣：

????????可以用三元組表表示為：{(1, 1, 1), (2, 3, 3), (4, 2, 4)}

????????除了三元組表，壓縮存儲稀疏矩陣還可以使用十字鏈表等其他方法。

參考文獻

稠密圖與稀疏圖判別 - 焓青 - 博客園

【數據結構】圖的基本概念—無/有向圖、權和網、完全圖、路徑與回路-阿里云開發者社區