一、多元線性回歸模型簡介
回歸分析是數據分析中最基礎也是最重要的分析工具,絕大多數的數據分析問題,都可以使用回歸的思想來解決。回歸分析的任務就是,通過研究自變量X和因變量Y的相關關系,嘗試去解釋Y的形成機制,進而達到通過X去預測Y的目的。
常見的回歸分析有五類:線性回歸、0-1回歸、定序回歸、計數回歸和生存回歸,其劃分的依據是因變量Y的類型。本篇主要講解多元線性回歸以及lasso回歸。
回歸分析的目的
- 識別重要變量
- 判斷相關性的方向
- 要估計權重(回歸系數)
回歸分析分類
| 類型 | 模型 | Y的特點 | 例子 |
| 線性回歸 | OLS、GLS(最小二乘) | 連續數值型變量 | GDP、產量、收入 |
| 0-1回歸 | logistic回歸 | 二值變量(0-1) | 是否違約、是否得病 |
| 定序回歸 | probit定序回歸 | 定序變量 | 等級評定(優良差) |
| 計數回歸 | 泊松回歸(泊松分布) | 計數變量 | 每分鐘車流量 |
| 生存回歸 | Cox等比例風險回歸 | 生存變量(截斷數據) | 企業、產品的壽命 |
二、適用賽題
解釋類問題
- 問一個因變量y由多個自變量x決定,探究這多個x和y的關系
- 解釋哪個x和y關系更緊密
預測類問題
- 由于回歸模型會得到一個擬合曲線,進而可以由這個曲線去預測一些值
- 不過注意,當要用擬合曲線預測的時候,擬合優度一定要大
三、模型流程

四、流程分析
注:回歸模型其中涉及到矩陣論、概率論與數理統計的知識,本篇不展開證明和講解。且推薦使用Stata軟件來進行多元線性回歸分析。
1.處理變量
我們得到了一組數據,要對數據進行分類
橫截面數據
- 在某一時點收集的不同對象的數據
- 例如:我們自己發放問卷得到的數據,全國各省份2018年GDP的數據,大一新生今年體測的得到的數據
時間序列數據
- 對同一對象在不同時間連續觀察所取得的數據
- 例如:從出生到現在,你的體重的數據(每年生日稱一次),中國歷年來GDP的數據,在某地方每隔一小時測得的溫度數據
面板數據
- 橫截面數據與時間序列數據綜合起來的一種數據資源
- 例如:2008-2018年,我國各省份GDP的數據
| 數據類型 | 常見建模方法 |
| 橫截面數據 | 多元線性回歸 |
| 時間序列數據 | 移動平均、指數平滑、ARIMA、GARCH、VAR、 協積 |
| 面板數據 | 固定效應和隨機效應、靜態面板和動態面板 |
現在給出多元線性回歸方程

無內生性(no endogeneity)要求所有解釋變量均與擾動項不相關,這個假定通常太強,因為解釋變量一般很多(比如,5-15個解釋變量),且需要保證它們全部外生。是否可能弱化此條件?答案是肯定的,如果你的解釋變量可以區分為核心解釋變量與控制變量兩類。
- 核心解釋變量:我們最感興趣的變量,因此我們特別希望得到對其系數的一致估計(當樣本容量無限增大時,收斂于待估計參數的真值)
- 控制變量:我們可能對于這些變量本身并無太大興趣,而之所以把它們也放入回歸方程,主要是為了“控制住”那些對被解釋變量有影響的遺漏因素
- 在實際應用中,我們只要保證核心解釋變量與μ不相關即可
如果自變量中有定性變量,例如性別、地域等,在回歸中要怎么處理呢?例如:我們要研究性別對于工資的影響(性別歧視)。這時候可以用到虛擬變量


Female就是一個虛擬變量。
為了避免完全多重共線性的影響,引入虛擬變量的個數一般是分類數減1。例如男女是兩類,就引入了一個Female;如果是區別全國34個省的人,就可以設置33個虛擬變量。
2.初次回歸
利用Stata得到初次回歸的結果后,需要檢驗結果的可靠性,如果可靠就可以解釋系數完成工作如果不可靠,還需要調整方法繼續回歸。
問題出在擾動項

橫截面數據容易出現異方差的問題;時間序列數據容易出現自相關的問題。
①異方差
如果擾動項存在異方差
- OLS估計出來的回歸系數是無偏、一致的
- 假設檢驗無法使用(構造的統計量失效了)
- OLS估計量不再是最優線性無偏估計量(BLUE)
如何檢驗是否存在異方差
BP檢驗

原假設:擾動項不存在異方差。P值小于0.05,說明在95%的置信水平下拒絕原假設,即我們認為擾動項存在異方差。
懷特檢驗

原假設:擾動項不存在異方差。P值小于0.05,說明在95%的置信水平下拒絕原假設,即我們認為擾動項存在異方差。
②多重共線性
自相關的問題就是多重共線性的問題
如何檢驗是否存在多重共線性

3.處理問題
①如何解決異方差
- 使用OLS + 穩健的標準誤。如果發現存在異方差,一種處理方法是,仍然進行OLS回歸,但使用穩健標準誤。這是最簡單,也是目前通用的方法。只要樣本容量較大,即使在異方差的情況下,若使用穩健標準誤,則所有參數估計、假設檢驗均可照常進行。換言之,只要使用了穩健標準誤,就可以與異方差“和平共處”了
- 廣義最小二乘估計法GLS。原理:方差較大的數據包含的信息較少,我們可以給予信息量大的數據(即方差較小的數據更大的權重)缺點:我們不知道擾動項真實的協方差矩陣,因此我們只能用樣本數據來估計,這樣得到的結果不穩健,存在偶然性
- Stock and Watson (2011)推薦,在大多數情況下應該使用“OLS +穩健標準誤”
②如何處理多重共線性
- 如果不關心具體的回歸系數,而只關心整個方程預測被解釋變量的能力,則通常可以不必理會多重共線性(假設你的整個方程是顯著的)。這是因為,多重共線性的主要后果是使得對單個變量的貢獻估計不準,但所有變量的整體效應仍可以較準確地估計
- 如果關心具體的回歸系數,但多重共線性并不影響所關心變量的顯著性,那么也可以不必理會。即使在有方差膨脹的情況下,這些系數依然顯著;如果沒有多重共線性,則只會更加顯著
- 如果多重共線性影響到所關心變量的顯著性,則需要增大樣本容量,剔除導致嚴重共線性的變量(不要輕易刪除哦,因為可能會有內生性的影響),或對模型設定進行修改
③逐步回歸分析
沒有太好的方法處理多重共線性問題,可以調整回歸的方式
向前逐步回歸(Forward selection)
- 將自變量逐個引入模型,每引入一個自變量后都要進行檢驗,顯著時才加入回歸模型
- 缺點:隨著以后其他自變量的引入,原來顯著的自變量也可能又變為不顯著了,但是,并沒有將其及時從回歸方程中剔除掉
向后逐步回歸(Backward elimination)
- 與向前逐步回歸相反,先將所有變量均放入模型,之后嘗試將其中一個自變量從模型中剔除,看整個模型解釋因變量的變異是否有顯著變化,之后將最沒有解釋力的那個自變量剔除。此過程不斷迭代,直到沒有自變量符合剔除的條件
- 缺點:一開始把全部變量都引入回歸方程,這樣計算量比較大。若對一些不重要的變量,一開始就不引入,這樣就可以減少一些計算。當然這個缺點隨著現在計算機的能力的提升,已經變得不算問題了
注意事項
- 向前逐步回歸和向后逐步回歸的結果可能不同
- 不要輕易使用逐步回歸分析,因為剔除了自變量后很有可能會產生新的問題,例如內生性問題(后面會介紹lasso回歸)
- 有沒有更加優秀的篩選方法?有的,那就是每種情況都嘗試一次,最終一共有2的k次方 - 1種可能。如果自變量很多,那么計算相當費時
4.解釋系數

這里也可以看到,引入了新的自變量價格后,對回歸系數的影響非常大。這就是遺漏變量導致的內生性的造成的。

伍德里奇的《計量經濟學導論,現代觀點》里,第六章176 -177頁有詳細的論述。取對數意味著原被解釋變量對解釋變量的彈性,即百分比的變化而不是數值的變化。目前,對于什么時候取對數還沒有固定的規則,但是有一些經驗法則
- 與市場價值相關的,例如,價格、銷售額、工資等都可以取對數
- 以年度量的變量,如受教育年限、工作經歷等通常不取對數
- 比例變量,如失業率、參與率等,兩者均可
- 變量取值必須是非負數,如果包含0,則可以對y取對數ln(1+y)
取對數的好處
- 減弱數據的異方差性
- 如果變量本身不符合正態分布,取了對數后可能漸近服從正態分布
- 模型形式的需要,讓模型具有經濟學意義
下面有四類模型回歸系數的解釋
- 一元線性回歸:y = a + bx + μ,x每增加1個單位,y平均變化b個單位
- 雙對數模型:?lny = a + blnx + μ,x每增加1%,y平均變化b%
- 半對數模型:?y = a + blnx + μ,x每增加1%,y平均變化b/100個單位
- 半對數模型:?lny = a + bx + μ,x每增加1個單位,y平均變化(100b)%
5.再次回歸
在前面已經介紹了如何解決存在異方差的情況。但是對于多重共線性并未有一個較好的解決方法,解決方法中的增大樣本量顯然不太現實,找點數據已經不容易了,還要增大樣本量。所以在不用后面的方法的情況下,一般都是將導致嚴重共線性的變量刪除。下面我們介紹lasso回歸。
和lasso回歸一起出來的,還有嶺回歸。事實上,回歸中關于自變量的選擇大有門道, 變量過多時可能會導致多重共線性問題造成回歸系數的不顯著,甚至造成OLS估計的失效。本篇介紹到的嶺回歸和lasso回歸在OLS回歸模型的損失函數上加上了不同的懲罰項,該懲罰項由回歸系數的函數構成。一方面,加入的懲罰項能夠識別出模型中不重要的變量,對模型起到簡化作用,可以看作逐步回歸法的升級版;另一方面,加入的懲罰項能夠讓模型變得可估計,即使之前的數據不滿足列滿秩。
和前面一樣,還是推薦使用Stata軟件分析。但大多數博客或講義上都是使用Python來做嶺回歸和lasso回歸的,因此有Python機器學習基礎的同學可以自己查閱相關的調用代碼。
另外,Stata中對于嶺回歸的估計有點bug,因此推薦用lasso回歸。
那么,什么時候用lasso回歸呢?
我們首先使用最一般的OLS對數據進行回歸,然后計算方差膨脹因子VIF,如果VIF > 10則說明存在多重共線性的問題,此時我們需要對變量進行篩選。
在前面我們提到可以使用逐步回歸法來篩選自變量,讓回歸中僅留下顯著的自變量來抵消多重共線性的影響,知道lasso回歸后,我們完全可以把lasso回歸視為逐步回歸法的進階版,我們可以使用lasso回歸來幫我們篩選出不重要的變量,步驟如下
- 判斷自變量的量綱是否一樣,如果不一樣則首先進行標準化的預處理;
- 對變量使用lasso回歸,記錄下lasso回歸結果表中回歸系數不為0的變量,這些變量就是最終我們要留下來的重要變量,其余未出現在表中的變量可視為引起多重共線性的不重要變量
在得到了重要變量后,我們實際上就完成了變量篩選,此時我們只將這些重要變量視為自變量,然后進行回歸,并分析回歸結果即可。(注意:此時的變量可以是標準化前的,也可以是標準化后的,因為lasso只起到變量篩選的目的)
五、補充
1.擬合優度較低怎么辦
- 回歸分為解釋型回歸和預測型回歸。預測型回歸一般才會更看重R2。解釋型回歸更多的關注模型整體顯著性以及自變量的統計顯著性和經濟意義顯著性即可
- 可以對模型進行調整,例如對數據取對數或者平方后再進行回歸
- 數據中可能有存在異常值或者數據的分布極度不均勻
2.標準化回歸系數
為了更為精準的研究影響評價量的重要因素(去除量綱的影響),我們可考慮使用標準化回歸系數。
對數據進行標準化,就是將原始數據減去它的均數后,再除以該變量的標準差,計算得到新的變量值,新變量構成的回歸方程稱為標準化回歸方程,回歸后相應可得到標準化回歸系數。
標準化系數的絕對值越大,說明對因變量的影響就越大(只關注顯著的回歸系數哦)。
3.對于線性的理解
線性假定并不要求初始模型都呈上述的嚴格線性關系,自變量與因變量可通過變量替換而轉化成線性模型。比如下面的都是線性模型
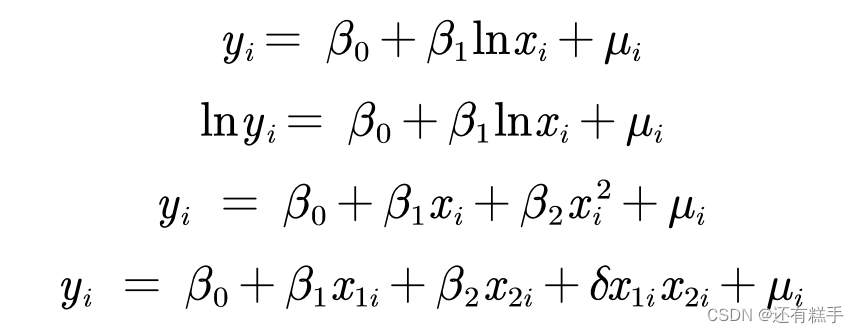





:坤坤的籃球回避秀)


)

)


![Linux基礎命令[9]-wc](http://pic.xiahunao.cn/Linux基礎命令[9]-wc)





)