目錄

?編輯

1. 算法效率

2. 時間復雜度

2.1 時間復雜度的概念

2.2 大O的表示漸進法

2.3? 一個栗子

3. 空間復雜度

4. 常見復雜度對比

?5. 完結散花

---

???????

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ? ? ?悟已往之不諫，知來者猶可追 ?

創作不易，寶子們！如果這篇文章對你們有幫助的話，別忘了給個免費的贊喲~

1. 算法效率

算法在編寫成可執行程序后，運行時需要耗費時間資源和空間(內存)資源 。因此衡量一個算法的好壞，一般是從時間和空間兩個維度來衡量的，即時間復雜度和空間復雜度。
時間復雜度主要衡量一個算法的運行快慢，而空間復雜度主要衡量一個算法運行所需要的額外空間。在計算機發展的早期，計算機的存儲容量很小。所以對空間復雜度很是在乎。但是經過計算機行業的迅速發展，計算機的存儲容量已經達到了很高的程度。所以我們如今已經不需要再特別關注一個算法的空間復雜度
?

2. 時間復雜度

2.1 時間復雜度的概念

時間復雜度的定義：在計算機科學中，算法的時間復雜度是一個函數，它定量描述了該算法的運行時間。一個算法執行所耗費的時間，從理論上說，是不能算出來的，只有你把你的程序放在機器上跑起來，才能知道。但是我們需要每個算法都上機測試嗎？是可以都上機測試，但是這很麻煩，所以才有了時間復雜度這個分析方式。一個算法所花費的時間與其中語句的執行次數成正比例，算法中的基本操作的執行次數，為算法的時間復雜度。
即：找到某條基本語句與問題規模N之間的數學表達式，就是算出了該算法的時間復雜度。
下面代碼中count++語句一共執行了幾次呢？????????

void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}

Func1 執行的基本操作次數 ：F（N）=N^2+2*N+10
N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010
實際中我們計算時間復雜度時，我們其實并不一定要計算精確的執行次數，而只需要大概執行次數，那么這里我們使用大O的漸進表示法。

2.2 大O的表示漸進法

大O符號（Big O notation）：是用于描述函數漸進行為的數學符號。
推導大O階方法：
1、用常數1取代運行時間中的所有加法常數。
2、在修改后的運行次數函數中，只保留最高階項。
3、如果最高階項存在且不是1，則去除與這個項目相乘的常數。得到的結果就是大O階。
使用大O的漸進表示法以后，Func1的時間復雜度為：O（N^2）
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
通過上面我們會發現大O的漸進表示法去掉了那些對結果影響不大的項，簡潔明了的表示出了執行次數。
另外有些算法的時間復雜度存在最好、平均和最壞情況：
最壞情況：任意輸入規模的最大運行次數(上界)
平均情況：任意輸入規模的期望運行次數
最好情況：任意輸入規模的最小運行次數(下界)
例如：在一個長度為N數組中搜索一個數據x
最好情況：1次找到
最壞情況：N次找到
平均情況：N/2次找到
在實際中一般情況關注的是算法的最壞運行情況，所以數組中搜索數據時間復雜度為O(N)

2.3? 一個栗子

int Fib(size_t n)
{if (n < 3)return 1;elsereturn Fib(n - 1) + Fib(n - 2);
}

上面代碼的時間復雜度是多少呢~

所以上面函數的時間復雜度為O（2^N）~

實際上，遞歸的時間復雜度等于遞歸次數*每次遞歸的執行次數

3. 空間復雜度

空間復雜度也是一個數學表達式，是對一個算法在運行過程中臨時占用存儲空間大小的量度 。
空間復雜度不是程序占用了多少bytes的空間，因為這個也沒太大意義，所以空間復雜度算的是變量的個數。
空間復雜度計算規則基本跟實踐復雜度類似，也使用大O漸進表示法。
注意：函數運行時所需要的棧空間(存儲參數、局部變量、一些寄存器信息等)在編譯期間已經確定好了，因此空間復雜度主要通過函數在運行時候顯式申請的額外空間來確定。
舉一個栗子啦~

int Fib(size_t n)
{if (n < 3)return 1;elsereturn Fib(n - 1) + Fib(n - 2);
}

?上面代碼的空間復雜度是多少呢~

實際上，對于遞歸來說，空間復雜度=遞歸次數（即遞歸深度）~

而該函數的最深的遞歸深度是n次，所以他的空間復雜度是O（N）~

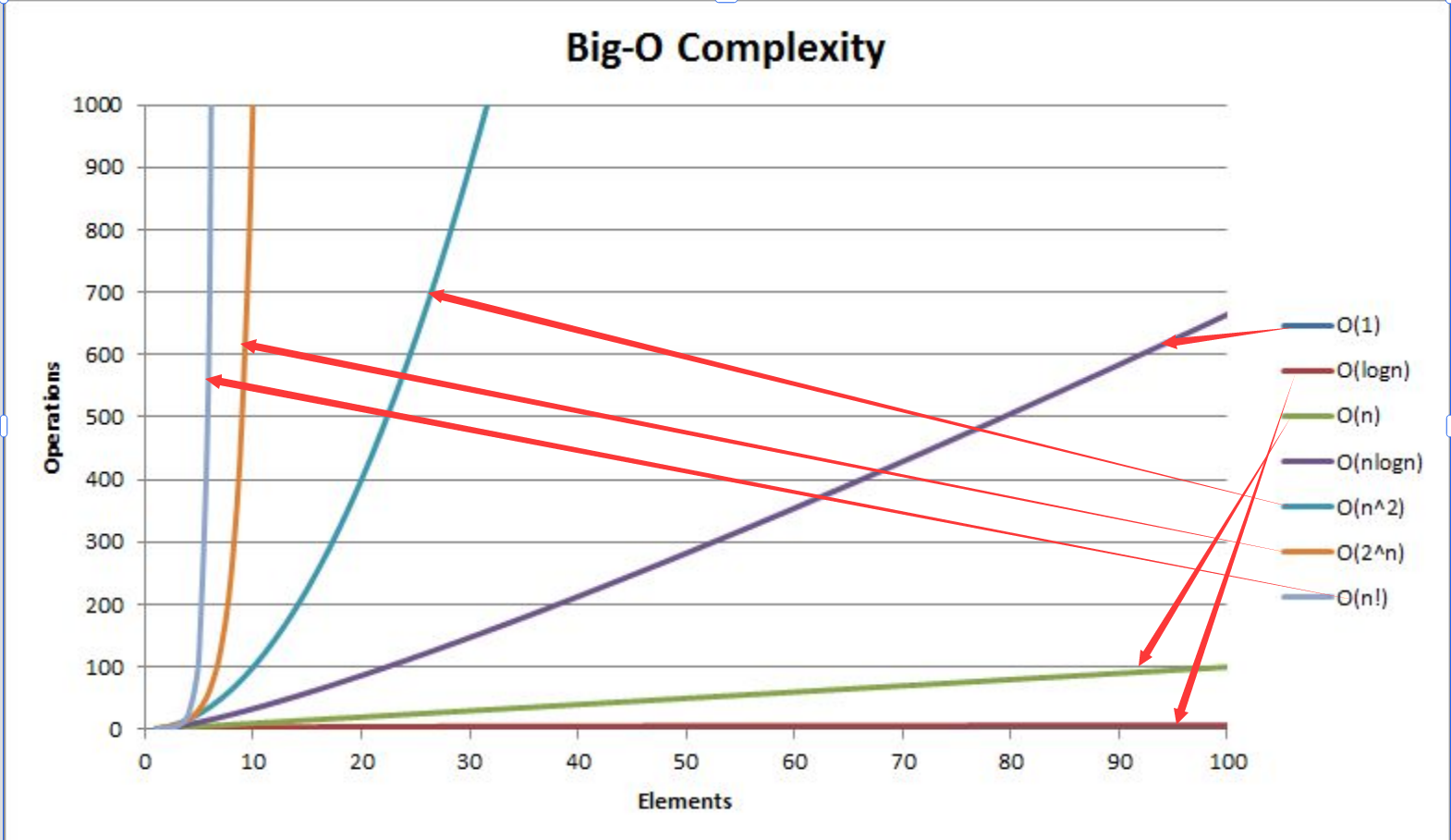
4. 常見復雜度對比

一般算法常見的復雜度如下~

?5. 完結散花

好了，這期的分享到這里就結束了~

如果這篇博客對你有幫助的話，可以用你們的小手指點一個免費的贊并收藏起來喲~

如果期待博主下期內容的話，可以點點關注，避免找不到我了呢~

我們下期不見不散~~