一、差分的特點和原理

對于一個數組a[]，差分數組diff[]的定義是:

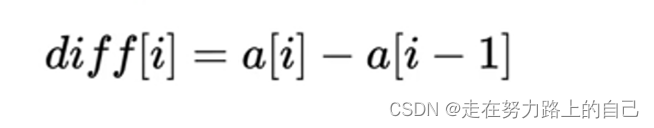
對差分數組做前綴和可以還原為原數組:

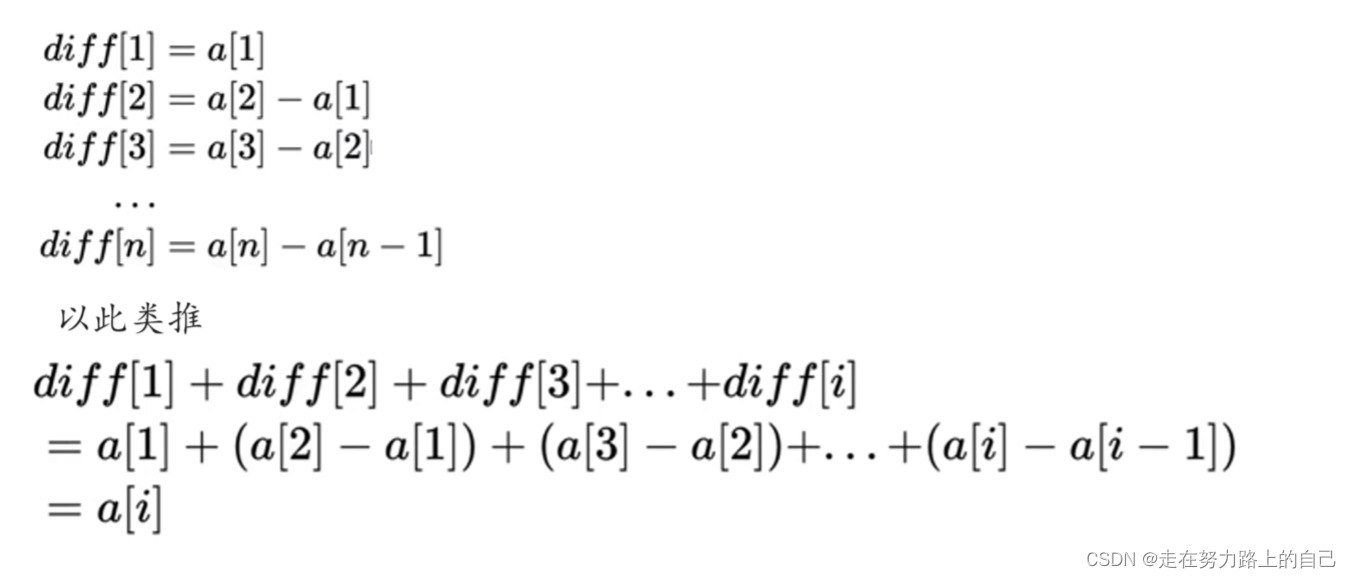
利用差分數組可以實現快速的區間修改，下面是將區間[l, r]都加上x的方法:

diff[l] += x;
diff[r + 1] -= x;

在修改完成后，需要做前綴和恢復為原數組，所以上面這段代碼的含義是:

diff[l]+=x表示將區間[l, n]都加上x但是[r+1,n]我們并不想加x，所以再將[r+1,n]減去x即可。

但是注意，差分數組不能實現“邊修改邊查詢(區間和)，只能實現"多次修改完成后多次查詢"。如果要實現“邊修改邊查詢”需要使用樹狀數組、線段樹等數據結構。

二、差分的實現

直接循環O(n)實現即可，注意這里建議使得a[0] = 0，下標從1開始。

for(int i = 1; i <= n; ++i)diff[i] = a[i] - a[i - 1];

將區間[l, r]都加上x：

diff[l] += x;
diff[r + 1] -= x;

三、區間更新

用戶登錄

問題描述

給定一個長度為 n 的數組 a[1], a[2], ..., a[n]。同時給定 m 個操作，每個操作包含三個整數數據 x, y, z。每個操作的意義是給數組中下標為 x 到下標為 y 之間（包括 x 和 y）的元素的值都加上 z。

輸入格式

輸入包含多組數據，數據組數不大于 5。

每組數據的第一行有兩個整數 n, m（0 < n, m < 100），分別表示數組的長度和操作的數量。

第二行有 n 個整數，分別代表 a[1], a[2], ..., a[n]（0 ≤ a[i] < 10）的初始值。

接下來 m 行，每行包含三個整數 x, y, z（1 ≤ x ≤ y ≤ n, 0 < z < 10），表示一個操作。

輸出格式

對于每組數據，輸出一行，包含這個序列的所有元素的值，并且每個值之間應該以空格隔開。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 9;
vector<int>a(N), b(N);void solve(int n, int m) {for (int i = 1; i <= n; i++)cin >> a[i];for (int i = 1; i <= n; i++)b[i] = a[i] - a[i - 1];// 初始化差分數組while (m--) {int l, r, x; cin >> l >> r >> x;b[l] += x; b[r + 1] -= x;  // 區間[l,r] [l]+x    [r+1]-x}for (int i = 1; i <= n; i++)a[i] = a[i - 1] + b[i];for (int i = 1; i <= n; i++)cout << a[i] << " \n"[i == n];必須是雙引號，\之前可以寫空格或者逗號
}
int main()
{int n, m;// 輸入 n, 表示 a[n] 的元素個數// 輸入 m, 表示 m 行while (cin >> n >> m)solve(n, m);return 0;
}

今天就先到這了！！！

看到這里了還不給博主扣個：
?? 點贊??收藏 ?? 關注！

你們的點贊就是博主更新最大的動力！
有問題可以評論或者私信呢秒回哦。