文章目錄
- 強化學習概念
- 實現
- qLearning
- 基于這個思路,那么解決這個問題的代碼如下
強化學習概念
強化學習有一個非常直觀的表現,就是從出發點到目標之間存在著一個連續的狀態轉換,比如說從狀態一到狀態456,而每一個狀態都有多種的行為,這些行為會有相應的懲罰和獎勵。比如走迷宮問題,每上下左右,或者靜止走一步都距離出口進入了不同的狀態
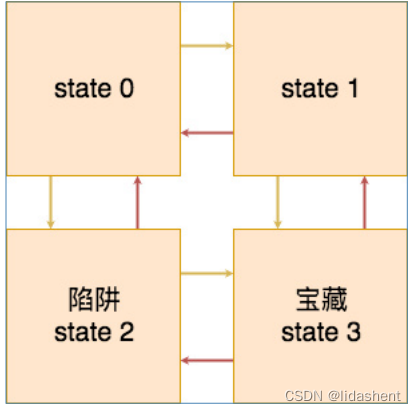
我們可以根據每一步進入的狀態得到不同的獎勵,從而找到出口.最后就得到了我們無論進入哪一個狀態,而預知的有益的下一步行動的獎勵表。
這樣就叫做環境狀態感知,將一個智能體隨機放入當前環境任何狀態,他都可以根據學到的決策表選擇最佳行動
接下來我們來實現這個走迷宮的問題。來具體的實踐 qlearning的基礎思想。
實現
狀態矩陣,如下矩陣中的每一行都代表了從出發點到目標之間的的每一個狀態,分別是狀態一,狀態二,狀態三,狀態4,而每一個狀態都有5種行動,分別是上下左右靜止,這個是四個狀態上下左右行為的狀態獎勵表,0表示行動不可以進行,-1表示行動可以進行,但是不是終點,10則表示是終點。-10是陷阱
解讀第一行就是狀態一無法向上,得到0分,向下扣10分,無法向左得0分,向右扣1分,靜止扣1分
reward = np.array([[0, -10, 0, -1, -1],[0, 10, -1, 0, -1],[-1, 0, 0, 10, -10],[-1, 0, -10, 0, 10]])
狀態轉移矩陣,這個矩陣表示的是,哪一個狀態可以向哪一個狀態進行遷移,分別是上下左右靜止所進入的狀態,負一表示無法進入新的狀態,零表示進入狀態0,一表示進入狀態一,二表示進入狀態二,三表示進入狀態三。
對應這四個狀態的五種行動,分別會進入到什么狀態中
解讀第一行就是狀態一向上無法進入新狀態,向下進入狀態2,向左無法進入新狀態,向右進入狀態1,靜止待在狀態0
transition_matrix = np.array([[-1, 2, -1, 1, 0],[-1, 3, 0, -1, 1],[0, -1, -1, 3, 2],[1, -1, 2, -1, 3]])
有效行動矩陣,這個矩陣表示了每一個狀態可行的行為。對應上面的狀態轉移矩陣。由此智能體無論落在哪一個狀態,他都可以選擇有效的行動。
valid_actions = np.array([[1, 3, 4],[1, 2, 4],[0, 3, 4],[0, 2, 4]])
綜上所述,我們定義了,智能體從出發到終點,每一個狀態的有效的行為,以及智能體如何進行狀態轉移。那么我們接下來所要求的是智能體無論落在哪一個狀態他都要快速而有效的找到終點,得到每一個狀態有效的行動獎勵表
我們初始化這個行動表,并設置收益系數為0.8,即是用來計算智能體在他可預見的行為里,每一個行為可以得到的收益.
q_matrix = np.zeros((4, 5))
gamma = 0.8
然后我們隨機將智能體放在任意的狀態上,并讓他隨機地選擇行動,我們來查看一下, Ta.所統計出的行動獎勵表,以及每一個行動以及所得到的收益。
for i in range(10):start_state = np.random.choice([0, 1, 2], size=1)[0] # 隨機初始起點print('start_state:{}'.format(start_state))current_state = start_statewhile current_state != 3: # 判斷是否到達終點action = random.choice(valid_actions[current_state]) # greedy 隨機選擇當前狀態下的有效動作next_state = transition_matrix[current_state][action] # 通過選擇的動作得到下一個狀態future_rewards = []for action_nxt in valid_actions[next_state]:future_rewards.append(q_matrix[next_state][action_nxt]) # 得到下一個狀態所有可能動作的獎勵q_state = reward[current_state][action] + gamma * max(future_rewards) # bellman equationq_matrix[current_state][action] = q_state # 更新 q 矩陣current_state = next_state # 將下一個狀態變成當前狀態print('episode: {}, q matrix: \n{}'.format(i, q_matrix))print()
我們上面這個程序是讓每一個智能體隨機的走,直到走出終點為止,然后對他所走過的路給出評分評價。我們可以先看到,第一次智能體落在了狀態0,它嘗試向右走,得到了-1分來到了狀態1,然后向左走來到狀態0,又是-1分,從狀態0又向下走到狀態2,得到了-10分,然后選擇靜止一次,扣了10分,最后從狀態2向右走到終點狀態3,得到10分,然后結束第一次嘗試,更新記憶表
我怎么看出來的?
我已經說了,每行代表的是每個狀態,每列代表的是上下左右靜止5個動作,你從狀態0去看,看看走哪個狀態會得到-10和-1,結合那個迷宮走向,根據得分就可以看出來

qLearning
從上面的基礎模型中我們知道,如果要尋找最佳行動策略,需要的事件數據有,當前環境狀態,可以進行的行為,當前環境每個行為的下一步獎勵,最后得到一個狀態獎勵表,表示從這個狀態里如何走才是最佳策略
問題是,現實世界不簡單啊,前面迷宮的狀態是有限的,格子總是有限的,動作和狀態還可以錄入,但是現實中狀態太多了.
我們將走迷宮問題改成下棋問題,比如圍棋,我們每走一步,都有幾百種落點可供選擇,預示著幾百個落點后棋盤會處于多少種不同的狀態,然后再次走一步,繼續是幾百種不同的狀態,我們要求ai下棋贏過我們,讓ai可以估計接下來的10步如何走才能形成優勢,讓ai記憶棋譜是行不通的,狀態太多了,狀態可以逼近了萬億種狀態,幾乎無窮無盡
如果可以讓ai自己探索,自己去學習和觀察其中有益的動作狀態,自己給自己喂數據,自己訓練自己,最后只根據結果完成的好不好來判定,那么就好了
神經網絡則提出了一種新的方式,不必知道所有的環境狀態,只需要讓神經網絡學習曾經經歷過的有益的狀態就可以了,就像人類一樣,形成經驗,我們可以把當前圍棋環境參數輸入神經網絡,讓神經網絡自主學習如何走出下一步,估計下一步得分,只要對局足夠多,神經網絡就會學習的足夠多,它就會根據有益的下棋經歷,形成一套自己的經驗價值獎勵表,至于其從對局中學習到了什么,我們是無從得知的,但是從實際結果上看,從aphaGO擊敗柯潔后,幾乎圍棋領域已經無人敢稱尊了
那么我們不必告訴神經網絡我們的環境中有多少種狀態,我們只需要告訴他環境參數是如何的,有幾種行動就可以了,讓它自己找到最佳策略
接下來我們來解決一下gym里經典的擺錘問題:
有一輛小車和一個豎桿,初始狀態下,桿子是傾斜的,要求智能體左右移動小車讓豎桿保持直立
如果豎桿偏移小車中心2個單位智能體就會失敗,相反桿子持續豎著,智能體堅持時間越長獎勵越多
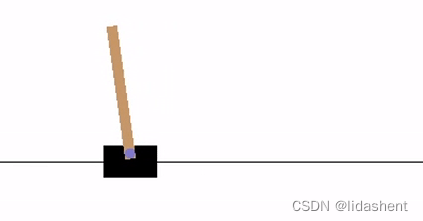
那么接下來就需要設計一下,如何讓神經網絡完成這個目標
先說一下目標,我們希望得到一個模型,這個模型可以根據環境狀態給出每個行動狀態的下一步狀態的獎勵預測,從而選擇最佳狀態去行動
那么我們這個神經網絡學習的目標就是如何準確預測當前狀態采取的每個行動所得到的獎勵,即是q值,這是我們的優化目標
正常來說,需要一個神經網絡A,根據當前的環境數據,動作數據,以及跟隨動作的下一步環境狀態反饋獎勵數據,讓這個A不斷的自我學習,預測出的行動獎勵和真實的環境獎勵貼近就可以了
但是實際訓練中,往往不會直接使用真實的環境獎勵,而是采取了緩步更新的方式
這種方式是這樣的:
策略網絡A:根據當前環境給出估計的下一步最優行動,給出估計獎勵值Q1
目標網絡B:根據當前環境給出下一步行動的估計獎勵值Q2
A與B的網絡結構一樣,A負責接收環境數據進行訓練更新參數,
目標網絡B不進行訓練,其參數來自于A的復制,但是其估算值Q2和當前環境下一步實際獎勵值Q進行一起計算得到Q3,Q3用于對A進行訓練,作為A的優化目標值進行A的網絡結構更新
B的參數隨著A的訓練緩步更新,B的參數復制更新總是遲滯于A,Q1向著Q3優化
這樣使用同一個網絡結構,B來引導A進行訓練
這主要是基于以下幾個問題考慮:
1.穩定性:使用目標網絡可以提供一種穩定的目標值來更新在策略網絡的Q值。如果直接使用策略網絡的Q值來更新,那么每次更新都可能導致目標值發生變化,這會使得學習過程更加不穩定。通過使用目標網絡,我們可以確保在一段時間內目標值是穩定的,這有助于算法的收斂。
2.減少過擬合:目標網絡的作用類似于深度學習中的dropout或正則化技術,它可以減少在線網絡對特定樣本的過擬合。如果每次更新都直接依賴于當前策略網絡的輸出,那么策略網絡可能會過于擬合當前的數據,導致泛化能力下降。
3.解耦目標和當前策略:使用目標網絡可以解耦目標Q值的計算和當前策略的選擇。這意味著我們可以獨立地更新目標網絡,而不需要在每個時間步都重新計算目標Q值。這提高了算法的效率。
4.平滑學習:目標網絡通過保持一定的穩定性,使得學習過程更加平滑。在每次更新時,我們不會引入太大的變化,這有助于算法逐步逼近最優解。
5.避免陷入局部最優:通過引入目標網絡,算法能夠在一定程度上避免陷入局部最優解。因為目標網絡提供的目標值是基于過去的策略和Q值估計,這有助于引導策略網絡探索更多的狀態空間
基于這個思路,那么解決這個問題的代碼如下
import time
import matplotlib.pyplot as plt
from IPython import display
import gymnasium as gym
import math
import random
import matplotlib
import matplotlib.pyplot as plt
from collections import namedtuple, deque
from itertools import count
import os
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import gymfrom gym import wrappersenv = gym.make("CartPole-v1",render_mode="human")
# set up matplotlib
is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:from IPython import display
# 開啟交互式繪圖模式。動態展示訓練過程
plt.ion()# if GPU is to be used
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 命名元組,狀態轉移變量,state: 表示當前狀態。
# action: 表示采取的動作。
# next_state: 表示轉移到的下一個狀態。
# reward: 表示從當前狀態到下一個狀態的獎勵
Transition = namedtuple('Transition',('state', 'action', 'next_state', 'reward'))# 經驗回放內存類
class ReplayMemory(object):# 經驗回放內存的容量。雙向隊列長度,maxlen 參數限制了隊列的最大長度,確保內存不會無限增長def __init__(self, capacity):self.memory = deque([], maxlen=capacity)# 保存一次狀態轉移,添加到內存隊列def push(self, *args):"""Save a transition"""self.memory.append(Transition(*args))# 從內存中隨機采樣一批狀態轉移def sample(self, batch_size):return random.sample(self.memory, batch_size)# 獲取內存中狀態轉移的數量def __len__(self):return len(self.memory)# 這個 DQN 模型是一個具有兩個隱藏層的前饋神經網絡,用于近似 Q-值函數
class DQN(nn.Module):# n_observations:表示輸入狀態的維度(觀測值的數量)。# n_actions:表示輸出動作的維度(動作的數量)def __init__(self, n_observations, n_actions):super(DQN, self).__init__()# 創建了一個線性層(nn.Linear),將輸入狀態映射到一個具有 128 個神經元的隱藏層。self.layer1 = nn.Linear(n_observations, 128)# 創建了第二個具有 128 個神經元的隱藏層self.layer2 = nn.Linear(128, 128)# 創建了一個線性層,將隱藏層的輸出映射到動作空間的維度。self.layer3 = nn.Linear(128, n_actions)# Called with either one element to determine next action, or a batch# during optimization. Returns tensor([[left0exp,right0exp]...]).# 調用這個方法來獲取模型的輸出。# 將輸入 x 通過 ReLU 激活函數傳遞給第一個隱藏層,然后再傳遞給第二個隱藏層。最后,我們返回輸出層的結果,表示不同動作的預期值。def forward(self, x):x = F.relu(self.layer1(x))x = F.relu(self.layer2(x))return self.layer3(x)# 每次訓練時從經驗回放內存中隨機選擇的狀態轉移的數量
BATCH_SIZE = 128
# 計算未來獎勵的折現值。較大的折扣因子意味著更重視未來獎勵
GAMMA = 0.99
# ε-貪心策略 中的參數。在訓練初期,智能體更傾向于探索新的動作(ε 較大)。
# 隨著訓練的進行,它逐漸減少探索,更傾向于選擇當前估計最優的動作(ε 較小)。
EPS_START = 0.9
EPS_END = 0.05
# 探索率(ε)的衰減速率。每隔一定步數,ε 會減小一次,以平衡探索和利用。
EPS_DECAY = 1000
# 目標網絡 更新的參數。目標網絡用于計算目標 Q-值,通過軟更新(滑動平均)來更新。較小的 TAU 值意味著更頻繁的更新目標網絡。
TAU = 0.005
# 調整模型權重的更新步長
LR = 1e-4
# 獲取了 OpenAI Gym 環境中的動作數量(n_actions),然后獲取了狀態觀測值的數量(n_observations)
# Get number of actions from gym action space
n_actions = env.action_space.n
# Get the number of state observations
state, info = env.reset()
n_observations = len(state)
# 主要模型,用于預測每個動作的 Q 值。它接受狀態觀測值作為輸入,并輸出每個動作的預期值。
policy_net = DQN(n_observations, n_actions).to(device)
# 目標網絡,用于計算目標 Q 值。在訓練過程中,它的參數會被軟更新(滑動平均)以穩定訓練。
target_net = DQN(n_observations, n_actions).to(device)
# 用于將 policy_net 的參數加載到 target_net 中,確保兩者初始狀態相同。可以使用 policy_net 進行訓練和推斷,同時使用 target_net 計算目標 Q 值
target_net.load_state_dict(policy_net.state_dict())
# 使用了 AdamW 優化器來訓練模型,并創建了一個經驗回放內存,用于存儲狀態轉移數據
optimizer = optim.AdamW(policy_net.parameters(), lr=LR, amsgrad=True)
memory = ReplayMemory(1000)steps_done = 0# 負責根據ε-貪心策略選擇動作
# 探索和利用之間的平衡由**探索率(epsilon)**控制。
# epsilon 越大,越傾向于探索(隨機選擇動作)。
# epsilon 值隨著時間衰減,以鼓勵智能體在學習過程中更多地進行利用。
def select_action(state):global steps_done# 生成一個介于 0 和 1 之間的隨機樣本。sample = random.random()# 根據當前 epsilon 值計算探索閾值。eps_threshold = EPS_END + (EPS_START - EPS_END) * \math.exp(-1. * steps_done / EPS_DECAY)steps_done += 1# 如果樣本大于閾值,選擇具有最高 Q 值的動作(利用)。if sample > eps_threshold:with torch.no_grad():# t.max(1) will return the largest column value of each row.# second column on max result is index of where max element was# found, so we pick action with the larger expected reward.return policy_net(state).max(1).indices.view(1, 1)# 否則,從動作空間中隨機采樣一個動作(探索)。else:return torch.tensor([[env.action_space.sample()]], device=device, dtype=torch.long)episode_durations = []# 繪制訓練過程中的回合持續時間(Duration),用于繪圖
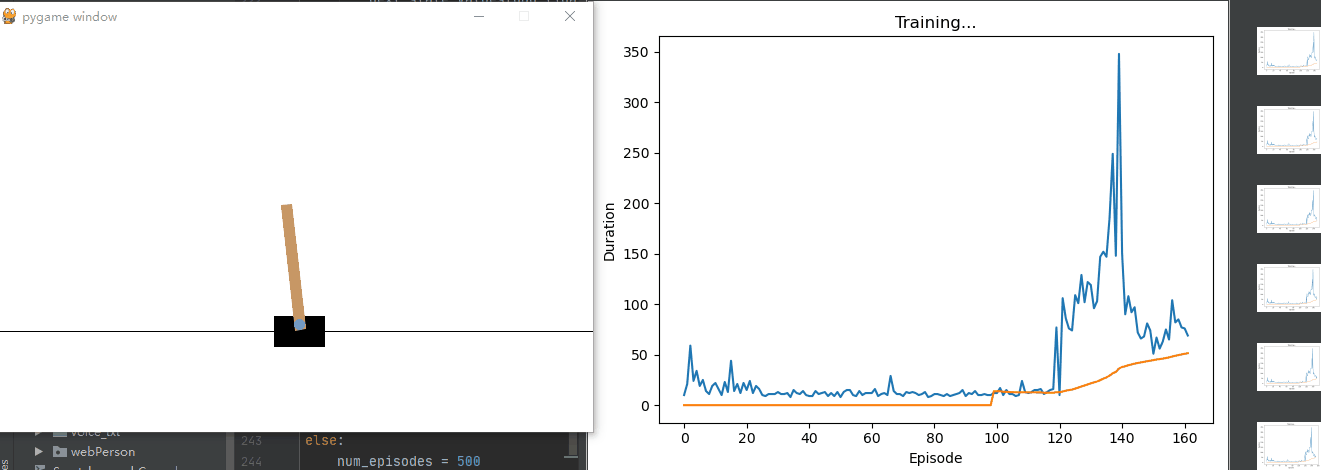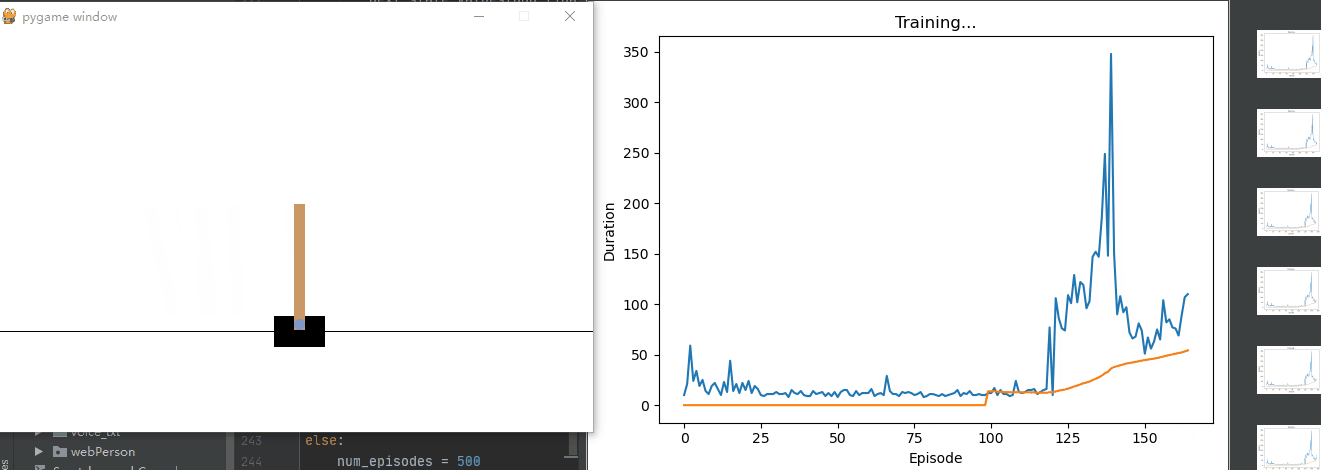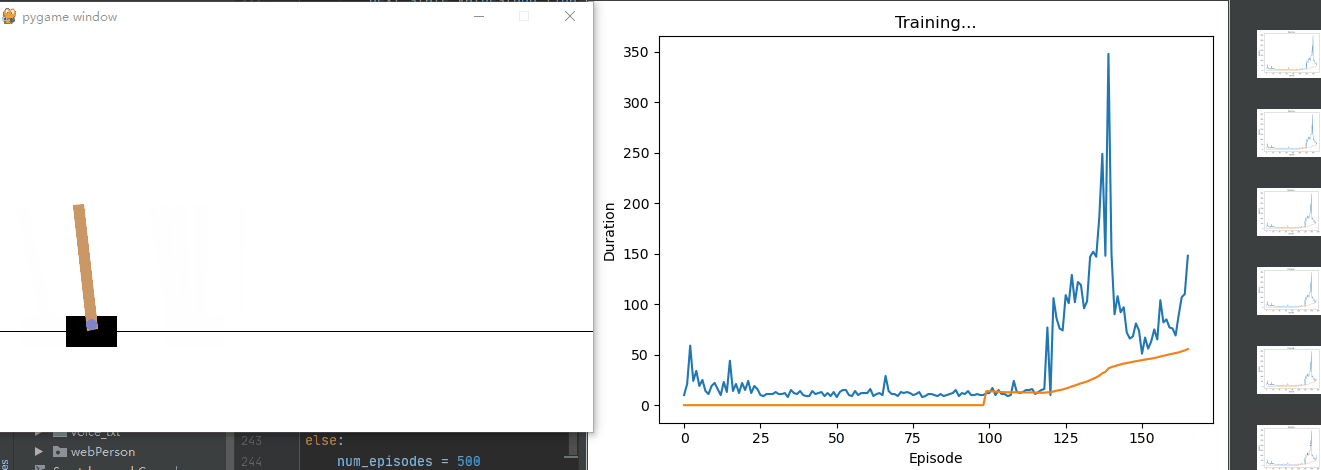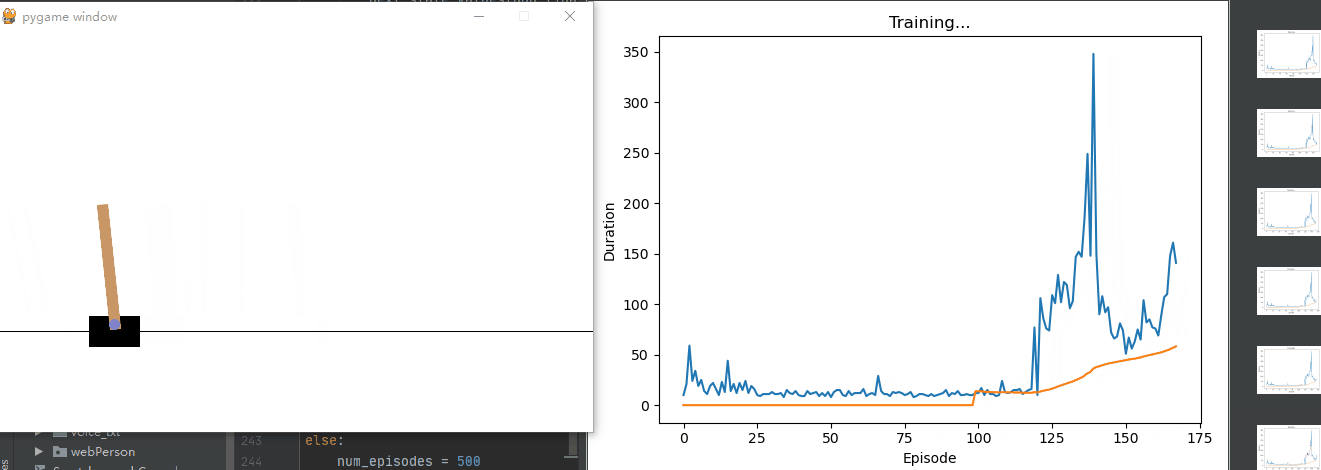
def plot_durations(show_result=False):# 創建一個名為 plt.figure(1) 的圖形。plt.figure(1)# 將回合持續時間(episode_durations)轉換為張量 durations_t。durations_t = torch.tensor(episode_durations, dtype=torch.float)# 如果 show_result 為真,標題設置為“Result”;否則,標題設置為“Training…”。if show_result:plt.title('Result')else:plt.clf()plt.title('Training...')# 橫軸表示回合數,縱軸表示持續時間。plt.xlabel('Episode')plt.ylabel('Duration')plt.plot(durations_t.numpy())# 繪制了回合持續時間的折線圖,并計算了最近 100 個回合的平均值。如果回合數超過 100,還會繪制平均值的折線圖。# 幫助我們可視化訓練過程中的回合持續時間# Take 100 episode averages and plot them tooif len(durations_t) >= 100:means = durations_t.unfold(0, 100, 1).mean(1).view(-1)means = torch.cat((torch.zeros(99), means))plt.plot(means.numpy())plt.pause(0.001) # pause a bit so that plots are updatedif is_ipython:if not show_result:display.display(plt.gcf())display.clear_output(wait=True)else:display.display(plt.gcf())# Deep Q-Network (DQN) 訓練過程中的關鍵部分
def optimize_model():# 如果回放內存的大小小于批次大小 (BATCH_SIZE),則提前返回(不進行優化)if len(memory) < BATCH_SIZE:return# 否則,從回放內存中隨機采樣一批過渡數據。transitions = memory.sample(BATCH_SIZE)# Transpose the batch (see https://stackoverflow.com/a/19343/3343043 for# detailed explanation). This converts batch-array of Transitions# to Transition of batch-arrays.# 轉置批處理(參見https://stackoverflow.com/a/19343/3343043# 詳細解釋)。這將轉換轉換的批處理數組# to批量數組的轉換。batch = Transition(*zip(*transitions))# Compute a mask of non-final states and concatenate the batch elements# (a final state would've been the one after which simulation ended)# 計算非最終狀態的掩碼,并連接批處理元素# (最終狀態是模擬結束后的狀態)non_final_mask = torch.tensor(tuple(map(lambda s: s is not None,batch.next_state)), device=device, dtype=torch.bool)non_final_next_states = torch.cat([s for s in batch.next_stateif s is not None])state_batch = torch.cat(batch.state)action_batch = torch.cat(batch.action)reward_batch = torch.cat(batch.reward)# 使用 policy_net 計算當前狀態-動作對的 Q 值。# Compute Q(s_t, a) - the model computes Q(s_t), then we select the# columns of actions taken. These are the actions which would've been taken# for each batch state according to policy_net# 計算Q(s_t, a) -模型計算Q(s_t),然后我們選擇# 所采取的行動列。這些都是應該采取的行動# 根據policy_net對應每個批處理狀態state_action_values = policy_net(state_batch).gather(1, action_batch)# Compute V(s_{t+1}) for all next states.# Expected values of actions for non_final_next_states are computed based# on the "older" target_net; selecting their best reward with max(1).values# This is merged based on the mask, such that we'll have either the expected# state value or 0 in case the state was final.# 計算所有下一個狀態的V(s_{t+1})# non_final_next_states的動作期望值是基于計算的# 在“舊的”target_net上;選擇最大(1)個值的最佳獎勵# 這是基于掩碼合并的,這樣我們就會有預期的# state值,如果狀態為final,則為0。# 使用 target_net 計算下一狀態的預期 Q 值。next_state_values = torch.zeros(BATCH_SIZE, device=device)with torch.no_grad():next_state_values[non_final_mask] = target_net(non_final_next_states).max(1).values# Compute the expected Q values# 計算預期 Q 值與當前 Q 值之間的均方誤差作為損失。通過反向傳播更新 policy_net 的參數。# 這個函數使用從回放內存中采樣的一批過渡數據來優化 policy_netexpected_state_action_values = (next_state_values * GAMMA) + reward_batch# SmoothL1Loss 是一種用于回歸任務的損失函數,它在絕對誤差和平方誤差之間取得平衡。# 在 DQN 訓練中,我們使用它來計算 Q 值的損失。這段代碼計算了損失并通過反向傳播更新了模型的參數# Compute Huber losscriterion = nn.SmoothL1Loss()loss = criterion(state_action_values, expected_state_action_values.unsqueeze(1))# Optimize the modeloptimizer.zero_grad()loss.backward()# In-place gradient clippingtorch.nn.utils.clip_grad_value_(policy_net.parameters(), 100)optimizer.step()if torch.cuda.is_available():num_episodes = 6000
else:num_episodes = 500for i_episode in range(num_episodes):# Initialize the environment and get it's state# 初始化環境并獲取初始狀態。env.render()state, info = env.reset()state = torch.tensor(state, dtype=torch.float32, device=device).unsqueeze(0)for t in count():# 在每個回合中,根據當前狀態選擇動作。action = select_action(state)# 執行動作,獲取獎勵和下一狀態。observation, reward, terminated, truncated, _ = env.step(action.item())reward = torch.tensor([reward], device=device)done = terminated or truncatedif terminated:next_state = Noneelse:next_state = torch.tensor(observation, dtype=torch.float32, device=device).unsqueeze(0)# 將過渡數據存儲到回放內存中。# Store the transition in memorymemory.push(state, action, next_state, reward)# Move to the next statestate = next_state# Perform one step of the optimization (on the policy network)optimize_model()# 執行一步優化,更新策略網絡的參數。# 軟更新目標網絡的權重。# Soft update of the target network's weights# θ′ ← τ θ + (1 ?τ )θ′target_net_state_dict = target_net.state_dict()policy_net_state_dict = policy_net.state_dict()for key in policy_net_state_dict:target_net_state_dict[key] = policy_net_state_dict[key] * TAU + target_net_state_dict[key] * (1 - TAU)target_net.load_state_dict(target_net_state_dict)# 如果回合結束,記錄回合持續時間并繪制圖表。if done:episode_durations.append(t + 1)plot_durations()print("Episode finished after {} timesteps".format(t + 1))breakprint('Complete')
plot_durations(show_result=True)
plt.ioff()
plt.show()等級考試試卷(一級) 測試卷2021年12月)







)








班課表)

