一、Adaboost算法
1.1 Adaboost分類算法
adaboost_discrete_c.py
import numpy as np
import copy
from ch4.decision_tree_C import DecisionTreeClassifierclass AdaBoostClassifier:"""adaboost分類算法:既可以做二分類、也可以做多分類,取決于基本分類器1. 同質學習器:非列表形式,按同種類型的基學習器構造2. 異質學習器:列表傳遞[logisticsregression, svm, cart, ...]"""def __init__(self, base_estimator=None, n_estimators=10, learning_rate=1.0):""":param base_estimator: 基學習器:param n_estimators: 基學習器的個數T:param learning_rate: 學習率,降低后續訓練的基分類器的權重,避免過擬合"""self.base_estimator = base_estimatorself.n_estimators = n_estimatorsself.learning_rate = learning_rate# 如果不提供基學習器,則默認按照深度為2的決策樹作為基分類器if self.base_estimator is None:self.base_estimator = DecisionTreeClassifier(max_depth=2)if type(base_estimator) != list:# 同質(同種類型)的分類器,深拷貝self.base_estimator = [copy.deepcopy(self.base_estimator)for _ in range(self.n_estimators)]else:# 異質(不同種類型)的分類器self.n_estimators = len(self.base_estimator)self.estimator_weights = [] # 每個基學習器的權重系數def fit(self, x_train, y_train):"""訓練AdaBoost每個基學習器,計算權重分布,每個基學習器的誤差率和權重系數α,:param x_train: 訓練集,二維數組:m * k:param y_train: 目標集:return:"""x_train, y_train = np.asarray(x_train), np.asarray(y_train)n_samples, n_class = x_train.shape[0], len(set(y_train)) # 樣本量,類別數sample_weight = np.ones(n_samples) # 為適應自寫的基學習器,設置樣本均勻權重為1.0# 針對每一個基學習器,根據帶有權重分布的訓練集訓練基學習器,計算相關參數for idx in range(self.n_estimators):# 1. 使用具有權重分布的Dm的訓練數據集學習,并預測self.base_estimator[idx].fit(x_train, y_train, sample_weight=sample_weight)# 只關心分類錯誤的,如果分類錯誤,則為0,正確則為1y_hat_0 = (self.base_estimator[idx].predict(x_train) == y_train).astype(int)# 2. 計算分類誤差率error_rate = sample_weight.dot(1.0 - y_hat_0) / n_samplesif error_rate > 0.5:self.estimator_weights.append(0) # 當前基分類器不起作用continue# 3. 計算基分類器的權重系數,考慮溢出alpha_rate = 0.5 * np.log((1 - error_rate) / error_rate + 1e-8) + np.log(n_class - 1)alpha_rate = min(10.0, alpha_rate) # 避免權重系數過大self.estimator_weights.append(alpha_rate)# 4. 更新樣本權重,為了適應多分類,yi*Gm(xi)計算np.power(-1.0, 1 - y_hat_0)sample_weight *= np.exp(-1.0 * alpha_rate * np.power(-1.0, 1 - y_hat_0))sample_weight = sample_weight / np.sum(sample_weight) * n_samples# 5. 更新estimator的權重系數,按照學習率for i in range(self.n_estimators):self.estimator_weights[i] *= np.power(self.learning_rate, i)def predict_proba(self, x_test):"""預測測試樣本所屬類別概率,軟投票:param x_test: 測試樣本集:return:"""x_test = np.asarray(x_test)# 按照加法模型,線性組合基學習器# 每個測試樣本,每個基學習器預測概率(10,[(0.68, 0.32),(0.55, 0.45)]...)y_hat_prob = np.sum([self.base_estimator[i].predict_proba(x_test) *self.estimator_weights[i] for i in range(self.n_estimators)], axis=0)return y_hat_prob / y_hat_prob.sum(axis=1, keepdims=True)def predict(self, x_test):"""預測測試樣本所屬類別:param x_test: 測試樣本集:return:"""return np.argmax(self.predict_proba(x_test), axis=1)1.2 Adaboost回歸算法
adaboost_regressor.py
import numpy as np
import copy
from ch4.decision_tree_R import DecisionTreeRegression # CARTclass AdaBoostRegressior:"""adaboost回歸算法:結合(集成)策略:加權中位數、預測值的平均加權1. 同質學習器,異質學習器2. 回歸誤差率依賴于相對誤差:平方誤差、線性誤差、指數誤差"""def __init__(self, base_estimator=None, n_estimators=10, learning_rate=1.0,loss="square", comb_strategy="weight_median"):""":param base_estimator: 基學習器:param n_estimators: 基學習器的個數T:param learning_rate: 學習率,降低后續訓練的基分類器的權重,避免過擬合:param loss: 損失函數:linear、square、exp:param comb_strategy: weight_median、weight_mean"""self.base_estimator = base_estimatorself.n_estimators = n_estimatorsself.learning_rate = learning_rateself.loss = loss # 相對誤差的損失函數self.comb_strategy = comb_strategy # 結合策略# 如果不提供基學習器,則默認按照深度為2的決策樹作為基分類器if self.base_estimator is None:self.base_estimator = DecisionTreeRegression(max_depth=2)if type(base_estimator) != list:# 同質(同種類型)的分類器,深拷貝self.base_estimator = [copy.deepcopy(self.base_estimator)for _ in range(self.n_estimators)]else:# 異質(不同種類型)的分類器self.n_estimators = len(self.base_estimator)self.estimator_weights = [] # 每個基學習器的權重系數def _cal_loss(self, y_true, y_hat):"""根據損失函數計算相對誤差:param y_true: 真值:param y_hat: 預測值:return:"""errors = np.abs(y_true - y_hat) # 絕對值誤差if self.loss.lower() == "linear": # 線性return errors / np.max(errors)elif self.loss.lower() == "square": # 平方errors_s = (y_true - y_hat) ** 2return errors_s / np.max(errors) ** 2elif self.loss.lower() == "exp": # 指數return 1 - np.exp(-errors / np.max(errors))else:raise ValueError("僅支持linear、square和exp...")def fit(self, x_train, y_train):"""Adaboost回歸算法,T個基學習器的訓練:1. 基學習器基于權重分布Dt的訓練集訓練2. 計算最大絕對誤差、相對誤差、回歸誤差率3. 計算當前ht的置信度4. 更新下一輪的權重分布:param x_train::param y_train::return:"""x_train, y_train = np.asarray(x_train), np.asarray(y_train)n_samples, n_class = x_train.shape[0], len(set(y_train)) # 樣本量,類別數sample_weight = np.ones(n_samples) # 為適應自寫的基學習器,設置樣本均勻權重為1.0for idx in range(self.n_estimators):# 1. 基學習器基于權重分布Dt的訓練集訓練以及預測self.base_estimator[idx].fit(x_train, y_train, sample_weight=sample_weight)y_hat = self.base_estimator[idx].predict(x_train) # 當前訓練集的預測值# 2. 計算最大絕對誤差、相對誤差、回歸誤差率errors = self._cal_loss(y_train, y_hat) # 相對誤差error_rate = np.dot(errors, sample_weight / n_samples) # 回歸誤差率# 3. 計算當前ht的置信度,基學習器的權重參數alpha_rate = error_rate / (1 - error_rate)self.estimator_weights.append(alpha_rate)# 4. 更新下一輪的權重分布sample_weight *= np.power(alpha_rate, 1 - errors)sample_weight = sample_weight / np.sum(sample_weight) * n_samples# 5. 計算基學習器的權重系數以及考慮學習率self.estimator_weights = np.log(1 / np.asarray(self.estimator_weights))for i in range(self.n_estimators):self.estimator_weights[i] *= np.power(self.learning_rate, i)def predict(self, x_test):"""Adaboost回歸算法預測,按照加權中位數以及加權平均兩種結合策略:param x_test: 測試樣本集:return:"""x_test = np.asarray(x_test)if self.comb_strategy == "weight_mean": # 加權平均self.estimator_weights /= np.sum(self.estimator_weights)# n * Ty_hat_mat = np.array([self.estimator_weights[i] *self.base_estimator[i].predict(x_test)for i in range(self.n_estimators)])# print(y_hat_mat.shape) (10, 5160)return np.sum(y_hat_mat, axis=0)elif self.comb_strategy == "weight_median": # 加權中位數# T個基學習器的預測結果構成一個二維數組(10, 5160)y_hat_mat = np.array([self.estimator_weights[i] *self.base_estimator[i].predict(x_test)for i in range(self.n_estimators)]).Tsorted_idx = np.argsort(y_hat_mat, axis=1) # 二維數組# 按照每個樣本預測值的升序排列序號,排序權重系數,然后累加計算weight_cdf = np.cumsum(self.estimator_weights[sorted_idx], axis=1)# 選擇最小的t,如下代碼產生二維bool數組median_or_above = weight_cdf >= 0.5 * weight_cdf[:, -1][:, np.newaxis]# print(median_idx)median_idx = np.argmax(median_or_above, axis=1) # 返回每個樣本的t索引值median_estimators = sorted_idx[np.arange(x_test.shape[0]), median_idx]return y_hat_mat[np.arange(x_test.shape[0]), median_estimators]1.3 SAMME算法
samme_r_muti_classifier.py?
import numpy as np
import copy
from ch4.decision_tree_C import DecisionTreeClassifierclass SAMMERClassifier:"""SAMME.R算法是將SAMME拓展到連續數值型的范疇。基學習器的輸出為連續型,一般為類別概率的預測值。"""def __init__(self, base_estimator=None, n_estimators=10):""":param base_estimator: 基學習器:param n_estimators: 基學習器的個數T"""self.base_estimator = base_estimatorself.n_estimators = n_estimators# 如果不提供基學習器,則默認按照深度為2的決策樹作為基分類器if self.base_estimator is None:self.base_estimator = DecisionTreeClassifier(max_depth=2)if type(base_estimator) != list:# 同質(同種類型)的分類器,深拷貝self.base_estimator = [copy.deepcopy(self.base_estimator)for _ in range(self.n_estimators)]else:# 異質(不同種類型)的分類器self.n_estimators = len(self.base_estimator)self.estimator_weights = [] # 每個基學習器的權重系數self.n_samples, self.n_class = None, None # 樣本量和類別數def _target_encoding(self, y_train):"""對目標值進行編碼:param y_train: 訓練目標集:return:"""self.n_samples, self.n_class = len(y_train), len(set(y_train))target = -1 / (self.n_class - 1) * np.ones((self.n_samples, self.n_class))for i in range(self.n_samples):target[i, y_train[i]] = 1 # 對應該樣本的類別所在編碼中的列改為1return targetdef fit(self, x_train, y_train):"""訓練SAMME.Rt每個基學習器,根據預測類別概率計算權重分布:param x_train: 訓練集,二維數組:m * k:param y_train: 目標集:return:"""x_train, y_train = np.asarray(x_train), np.asarray(y_train)target = self._target_encoding(y_train) # 編碼sample_weight = np.ones(self.n_samples) # 為適應自寫的基學習器,設置樣本均勻權重為1.0# 針對每一個基學習器,根據帶有權重分布的訓練集訓練基學習器,計算相關參數c = (self.n_class - 1) / self.n_classfor idx in range(self.n_estimators):# 1. 使用具有權重分布的Dm的訓練數據集學習,并預測self.base_estimator[idx].fit(x_train, y_train, sample_weight=sample_weight)# 根據訓練的基學習器,獲得其樣本的預測類別概率pred_p = self.base_estimator[idx].predict_proba(x_train)# 針對預測概率,小于eps的值替換為eps,避免log函數溢出np.clip(pred_p, np.finfo(pred_p.dtype).eps, None, out=pred_p)# 2. 更新樣本權重sample_weight *= np.exp(-c * (target * np.log(pred_p)).sum(axis=1))sample_weight = sample_weight / np.sum(sample_weight) * self.n_samples@staticmethoddef softmax_func(x):"""softmax函數,為避免上溢或下溢,對參數x做限制:param x: 數組: batch_size * n_classes:return: 1 * n_classes"""exps = np.exp(x - np.max(x)) # 避免溢出,每個數減去其最大值exp_sum = np.sum(exps, axis=1, keepdims=True)return exps / exp_sumdef predict_proba(self, x_test):"""預測測試樣本所屬類別概率,軟投票:param x_test: 測試樣本集:return:"""x_test = np.asarray(x_test)C_x = np.zeros((x_test.shape[0], self.n_class))for i in range(self.n_estimators):y_prob = self.base_estimator[i].predict_proba(x_test)np.clip(y_prob, np.finfo(y_prob.dtype).eps, None, out=y_prob)y_ln = np.log(y_prob)C_x += (self.n_class - 1) * (y_ln - np.sum(y_ln, axis=1, keepdims=True) / self.n_class)return C_xdef predict(self, x_test):"""預測測試樣本所屬類別:param x_test: 測試樣本集:return:"""return np.argmax(self.predict_proba(x_test), axis=1)1.4?Adaboost分類算法測試
test_adaboost_c.py
from sklearn.datasets import make_classification
from sklearn.metrics import classification_reportfrom ch4.decision_tree_C import DecisionTreeClassifier # 基學習器,決策樹
from ch3.logistic_regression_2class import LogisticRegression # 邏輯回歸
from ch6.svm_smo_classifier import SVMClassifier # 支持向量機
from adaboost_discrete_c import AdaBoostClassifier
from ch8.plt_decision_function import plot_decision_functionX, y = make_classification(n_samples=300, n_features=2, n_informative=1, n_redundant=0, n_repeated=0, n_classes=2,n_clusters_per_class=1, class_sep=1, random_state=42)
# 同質:同種類型的基學習器
base_tree = DecisionTreeClassifier(max_depth=3, is_feature_all_R=True, max_bins=20)
ada_bc = AdaBoostClassifier(base_estimator=base_tree, n_estimators=10, learning_rate=1.0)
ada_bc.fit(X, y) # adaboost訓練
print("基學習器的權重系數:\n", ada_bc.estimator_weights)
y_pred = ada_bc.predict(X) # 預測類別
print(classification_report(y, y_pred))
plot_decision_function(X, y, ada_bc)# 異質:不同類型的基學習器
log_reg = LogisticRegression(batch_size=20, max_epochs=5)
cart = DecisionTreeClassifier(max_depth=4, is_feature_all_R=True)
svm = SVMClassifier(C=5.0, max_epochs=20)
ada_bc2 = AdaBoostClassifier(base_estimator=[log_reg, cart, svm], learning_rate=1.0)
ada_bc2.fit(X, y) # adaboost訓練
print("異質基學習器的權重系數:", ada_bc2.estimator_weights)
y_pred = ada_bc2.predict(X) # 預測類別
print(classification_report(y, y_pred))
plot_decision_function(X, y, ada_bc2)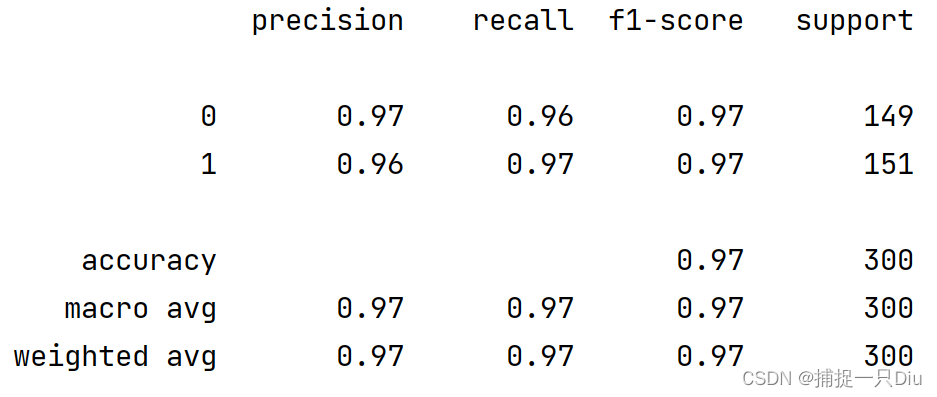

?test_adaboost_c2.py
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score
from sklearn.datasets import make_blobs
from ch4.decision_tree_C import DecisionTreeClassifier
from ch8.adaboost_discrete_c import AdaBoostClassifierX, y = make_blobs(n_samples=1000, n_features=10, centers=5, cluster_std=[1.5, 2, 0.9, 3, 2.8], random_state=0)
X = StandardScaler().fit_transform(X)base_em = DecisionTreeClassifier(max_depth=4, is_feature_all_R=True, max_bins=10)
acc_scores = [] # 存儲每次交叉驗證的均分
# 用10折交叉驗證評估不同基學習器個數T下的分類正確率
for n in range(1, 21):scores = [] # 一次交叉驗證的acc均值k_fold = KFold(n_splits=10)for idx_train, idx_test in k_fold.split(X, y):classifier = AdaBoostClassifier(base_estimator=base_em, n_estimators=n, learning_rate=1)classifier.fit(X[idx_train, :], y[idx_train])y_test_pred = classifier.predict(X[idx_test, :])scores.append(accuracy_score(y[idx_test], y_test_pred))acc_scores.append(np.mean(scores))print(n, ":", acc_scores[-1])plt.figure(figsize=(7, 5))
plt.plot(range(1, 21), acc_scores, "ko-", lw=1)
plt.xlabel("Number of Estimations", fontdict={"fontsize": 12})
plt.ylabel("Accuracy Score", fontdict={"fontsize": 12})
plt.title("Cross Validation Scores of Different Number of Base Learners", fontdict={"fontsize": 14})
plt.grid(ls=":")
plt.show()
1.5?Adaboost回歸算法測試
test_adaboost_regressor.py
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import r2_score
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from ch4.decision_tree_R import DecisionTreeRegression
from ch8.adaboost_regressor import AdaBoostRegressiorhousing = fetch_california_housing()
X, y = housing.data, housing.target
# print(X.shape)
# print(y.shape)
X = StandardScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)base_ht = DecisionTreeRegression(max_bins=50, max_depth=5)
plt.figure(figsize=(14, 15))def train_plot(cs, loss, i):abr = AdaBoostRegressior(base_estimator=base_ht, n_estimators=30,comb_strategy=cs, loss=loss)abr.fit(X_train, y_train)y_hat = abr.predict(X_test)# print(r2_score(y_test, y_hat))plt.subplots(231 + i)idx = np.argsort(y_test) # 對真值排序plt.plot(y_test[idx], "k-", lw=1.5, label="Test True")plt.plot(y_hat[idx], "r-", lw=1, label="Predict")plt.legend(frameon=False)plt.title("%s, %s, R2 = %.5f, MSE = %.5f" %(cs, loss, r2_score(y_test, y_hat), ((y_test - y_hat) ** 2).mean()))plt.xlabel("Test Samples Serial Number", fontdict={"fontsize": 12})plt.ylabel("True VS Predict", fontdict={"fontsize": 12})plt.grid(ls=":")print(cs, loss)loss_func = ["linear", "square", "exp"]
comb_strategy = ["weight_mean", "weight_median"]
i = 0
for loss in loss_func:for cs in comb_strategy:train_plot(cs, loss, i)i += 1
plt.show()
?1.6 SAMME算法測試
test_samme_r_c.py
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score
from sklearn.datasets import make_blobs
# from ch4.decision_tree_C import DecisionTreeClassifierR
from sklearn.tree import DecisionTreeClassifier
from ch8.samme_r_muti_classifier import SAMMERClassifierX, y = make_blobs(n_samples=1000, n_features=10, centers=5, cluster_std=[1.5, 2, 0.9, 3, 2.8], random_state=0)
X = StandardScaler().fit_transform(X)base_em = DecisionTreeClassifier(max_depth=4)
acc_scores = [] # 存儲每次交叉驗證的均分
# 用10折交叉驗證評估不同基學習器個數T下的分類正確率
for n in range(1, 21):scores = [] # 一次交叉驗證的acc均值k_fold = KFold(n_splits=10)for idx_train, idx_test in k_fold.split(X, y):classifier = SAMMERClassifier(base_estimator=base_em, n_estimators=n)classifier.fit(X[idx_train, :], y[idx_train])y_test_pred = classifier.predict(X[idx_test, :])scores.append(accuracy_score(y[idx_test], y_test_pred))acc_scores.append(np.mean(scores))print(n, ":", acc_scores[-1])plt.figure(figsize=(7, 5))
plt.plot(range(1, 21), acc_scores, "ko-", lw=1)
plt.xlabel("Number of Estimations", fontdict={"fontsize": 12})
plt.ylabel("Accuracy Score", fontdict={"fontsize": 12})
plt.title("Cross Validation Scores of Different Number of Base Learners", fontdict={"fontsize": 14})
plt.grid(ls=":")
plt.show()
1.7 可視化分類邊界函數
?plt_decision_function.py
import matplotlib.pyplot as plt
import numpy as npdef plot_decision_function(X, y, clf, is_show=True):"""可視化分類邊界函數:param X: 測試樣本:param y: 測試樣本的類別:param clf: 分類模型:param is_show: 是否在當前顯示圖像,用于父函數繪制子圖:return:"""if is_show:plt.figure(figsize=(7, 5))x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1xi, yi = np.meshgrid(np.linspace(x_min, x_max, 100),np.linspace(y_min, y_max, 100))y_pred = clf.predict(np.c_[xi.ravel(), yi.ravel()]) # 模型預測值y_pred = y_pred.reshape(xi.shape)plt.contourf(xi, yi, y_pred, cmap="winter", alpha=0.4)plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors="k")plt.xlabel("Feature 1", fontdict={"fontsize": 12})plt.ylabel("Feature 2", fontdict={"fontsize": 12})plt.title("Model Classification Boundary", fontdict={"fontsize": 14})if is_show:plt.show()二、提升樹算法boosting tree
2.1 提升樹回歸算法
boostingtree_r.py
import numpy as np
import copy
from ch4.decision_tree_R import DecisionTreeRegression # CARTclass BoostTreeRegressor:"""提升樹回歸算法,采用平方誤差損失"""def __init__(self, base_estimator=None, n_estimators=10, learning_rate=1.0):""":param base_estimator: 基學習器:param n_estimators: 基學習器的個數T:param learning_rate: 學習率,降低后續訓練的基分類器的權重,避免過擬合"""self.base_estimator = base_estimatorself.n_estimators = n_estimatorsself.learning_rate = learning_rate# 如果不提供基學習器,則默認按照深度為2的決策樹作為基分類器if self.base_estimator is None:self.base_estimator = DecisionTreeRegression(max_depth=2)if type(base_estimator) != list:# 同質(同種類型)的分類器,深拷貝self.base_estimator = [copy.deepcopy(self.base_estimator)for _ in range(self.n_estimators)]else:# 異質(不同種類型)的分類器self.n_estimators = len(self.base_estimator)def fit(self, x_train, y_train):"""提升樹的訓練,針對每個基決策樹算法,擬合上一輪的殘差:param x_train: 訓練集:param y_train: 目標集:return:"""x_train, y_train = np.asarray(x_train), np.asarray(y_train)# 1. 訓練第一棵回歸決策樹,并預測self.base_estimator[0].fit(x_train, y_train)y_hat = self.base_estimator[0].predict(x_train)y_residual = y_train - y_hat # 殘差,MSE的負梯度# 2. 從第二棵樹開始,每一輪擬合上一輪的殘差for idx in range(1, self.n_estimators):self.base_estimator[idx].fit(x_train, y_residual) # 擬合殘差# 累加第m-1棵樹的預測值,當前模型是f_(m-1)y_hat += self.base_estimator[idx].predict(x_train) * self.learning_ratey_residual = y_train - y_hat # 當前模型的殘差def predict(self, x_test):"""回歸提升樹的預測:param x_test: 測試樣本集:return:"""x_test = np.asarray(x_test)y_hat_mat = np.sum([self.base_estimator[0].predict(x_test)] +[np.power(self.learning_rate, i) * self.base_estimator[i].predict(x_test)for i in range(1, self.n_estimators - 1)] +[self.base_estimator[-1].predict(x_test)], axis=0)return y_hat_mat2.2 梯度提升樹分類算法
gradientboosting_c
import numpy as np
import copy
from ch4.decision_tree_R import DecisionTreeRegression # CARTclass GradientBoostClassifier:"""梯度提升樹多分類算法:多分類也可用回歸樹來做,即訓練與類別數相同的幾組回歸樹,每一組代表一個類別,然后對所有組的輸出進行softmax操作將其轉換為概率分布,再通過交叉熵或者KL一類的損失函數求每棵樹相應的負梯度,指導下一輪的訓練。"""def __init__(self, base_estimator=None, n_estimators=10, learning_rate=1.0):""":param base_estimator: 基學習器:param n_estimators: 基學習器的個數T:param learning_rate: 學習率,降低后續訓練的基分類器的權重,避免過擬合"""self.base_estimator = base_estimatorself.n_estimators = n_estimatorsself.learning_rate = learning_rate# 如果不提供基學習器,則默認按照深度為2的決策樹作為基分類器if self.base_estimator is None:self.base_estimator = DecisionTreeRegression(max_depth=2)if type(base_estimator) != list:# 同質(同種類型)的分類器,深拷貝self.base_estimator = [copy.deepcopy(self.base_estimator)for _ in range(self.n_estimators)]else:# 異質(不同種類型)的分類器self.n_estimators = len(self.base_estimator)self.base_estimators = [] # 擴展到class_num組分類器@staticmethoddef one_hot_encoding(target):class_labels = np.unique(target)target_y = np.zeros((len(target), len(class_labels)), dtype=np.int32)for i, label in enumerate(target):target_y[i, label] = 1 # 對應類別所在的列為1return target_y@staticmethoddef softmax_func(x):exps = np.exp(x - np.max(x))return exps / np.sum(exps, axis=1, keepdims=True)def fit(self, x_train, y_train):"""梯度提升分類算法的訓練,共訓練M * K個基學習器:param x_train: 訓練集:param y_train: 目標集:return:"""x_train, y_train = np.asarray(x_train), np.asarray(y_train)class_num = len(np.unique(y_train)) # 類別數y_encoded = self.one_hot_encoding(y_train)# 深拷貝class_num組分類器,每組(每個類別)n_estimators個基學習器# 假設是三分類:[[0, 1, 2, ..., 9], [10], [10]]self.base_estimators = [copy.deepcopy(self.base_estimator) for _ in range(class_num)]# 初始化第一輪基學習器,針對每個類別,分別訓練一個基學習器y_hat_scores = [] # 用于存儲每個類別的預測值for c_idx in range(class_num):self.base_estimators[c_idx][0].fit(x_train, y_encoded[:, c_idx])y_hat_scores.append(self.base_estimators[c_idx][0].predict(x_train))y_hat_scores = np.c_[y_hat_scores].T # 把每個類別的預測值構成一列,(120, 3) (n_samples, class_num)# print(np.asarray(y_hat_vals).shape)grad_y = y_encoded - self.softmax_func(y_hat_scores) # 按類別計算樣本的負梯度值# 訓練后續基學習器,共M - 1輪,每輪針對每個類別,分別訓練一個基學習器for idx in range(1, self.n_estimators):y_hat_values = [] # 用于存儲每個類別的預測值for c_idx in range(class_num):self.base_estimators[c_idx][idx].fit(x_train, grad_y[:, c_idx])y_hat_values.append(self.base_estimators[c_idx][idx].predict(x_train))y_hat_scores += np.c_[y_hat_values].T * self.learning_rate# print(np.asarray(y_hat_vals).shape)grad_y = y_encoded - self.softmax_func(y_hat_scores) # 按類別計算樣本的負梯度值def predict_proba(self, x_test):"""預測測試樣本所屬類別的概率:param x_test: 測試樣本集:return:"""x_test = np.asarray(x_test)y_hat_scores = []for c_idx in range(len(self.base_estimators)):# 取當前類別的M個基學習器estimator = self.base_estimators[c_idx]y_hat_scores.append(np.sum([estimator[0].predict(x_test)] +[self.learning_rate * estimator[i].predict(x_test)for i in range(1, self.n_estimators - 1)] +[estimator[-1].predict(x_test)], axis=0))# y_hat_scores的維度(3 * 30)return self.softmax_func(np.c_[y_hat_scores].T)def predict(self, x_test):"""預測測試樣本所屬類別,概率大的idx標記為類別:param x_test: 測試樣本集:return:"""print(self.predict_proba(x_test))return np.argmax(self.predict_proba(x_test), axis=1)
?2.3?梯度提升樹回歸算法
gradientboosting_r
import numpy as np
import copy
from ch4.decision_tree_R import DecisionTreeRegression # CARTclass GradientBoostRegressor:"""梯度提升樹回歸算法,損失函數:五個,以損失函數在當前模型的負梯度近似為殘差"""def __init__(self, base_estimator=None, n_estimators=10, learning_rate=1.0,loss="ls", huber_threshold=0.1, quantile_threshold=0.5):""":param base_estimator: 基學習器:param n_estimators: 基學習器的個數T:param learning_rate: 學習率,降低后續訓練的基分類器的權重,避免過擬合"""self.base_estimator = base_estimatorself.n_estimators = n_estimatorsself.learning_rate = learning_rate# 如果不提供基學習器,則默認按照深度為2的決策樹作為基分類器if self.base_estimator is None:self.base_estimator = DecisionTreeRegression(max_depth=2)if type(base_estimator) != list:# 同質(同種類型)的分類器,深拷貝self.base_estimator = [copy.deepcopy(self.base_estimator)for _ in range(self.n_estimators)]else:# 異質(不同種類型)的分類器self.n_estimators = len(self.base_estimator)self.loss = loss # 損失函數的類型self.huber_threshold = huber_threshold # 僅對Huber損失有效self.quantile_threshold = quantile_threshold # 僅對分位數損失函數有效def _cal_negative_gradient(self, y_true, y_pred):"""計算負梯度值:param y_true: 真值:param y_pred: 預測值:return:"""if self.loss.lower() == "ls": # MSEreturn y_true - y_predelif self.loss.lower() == "lae": # MAEreturn np.sign(y_true - y_pred)elif self.loss.lower() == "huber": # 平滑平均絕對損失return np.where(np.abs(y_true - y_pred) > self.huber_threshold,self.huber_threshold * np.sign(y_true - y_pred),y_true - y_pred)elif self.loss.lower() == "quantile": # 分位數損失return np.where(y_true > y_pred, self.quantile_threshold,self.quantile_threshold - 1)elif self.loss.lower() == "logcosh": # 雙曲余弦的對數的負梯度return -np.tanh(y_pred - y_true)else:raise ValueError("僅限于ls、lae、huber、quantile和logcosh,選擇有誤...")def fit(self, x_train, y_train):"""提升樹的訓練,針對每個基決策樹算法,擬合上一輪的殘差1. 假設回歸決策樹以mse構建的,針對不同的損失函數,計算不同的基尼指數劃分標準2. 預測,集成,也根據不同的損失函數,預測葉子結點的輸出...:param x_train: 訓練集:param y_train: 目標集:return:"""x_train, y_train = np.asarray(x_train), np.asarray(y_train)# 1. 訓練第一棵回歸決策樹,并預測self.base_estimator[0].fit(x_train, y_train)y_hat = self.base_estimator[0].predict(x_train)y_residual = self._cal_negative_gradient(y_train, y_hat) # 負梯度# 2. 從第二棵樹開始,每一輪擬合上一輪的殘差for idx in range(1, self.n_estimators):self.base_estimator[idx].fit(x_train, y_residual) # 擬合殘差# 累加第m-1棵樹的預測值,當前模型是f_(m-1)y_hat += self.base_estimator[idx].predict(x_train) * self.learning_ratey_residual = self._cal_negative_gradient(y_train, y_hat) # 負梯度def predict(self, x_test):"""回歸提升樹的預測:param x_test: 測試樣本集:return:"""x_test = np.asarray(x_test)y_hat_mat = np.sum([self.base_estimator[0].predict(x_test)] +[np.power(self.learning_rate, i) * self.base_estimator[i].predict(x_test)for i in range(1, self.n_estimators - 1)] +[self.base_estimator[-1].predict(x_test)], axis=0)return y_hat_mat?2.4 提升樹算法測試
test_boosting_tree_r.py
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import r2_score
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from ch4.decision_tree_R import DecisionTreeRegression
from ch8.boostingtree_r import BoostTreeRegressor
from sklearn.tree import DecisionTreeRegressor# housing = fetch_california_housing()
# X, y = housing.data[0:20000:100, :], housing.target[0:20000:100]
# print(X.shape)
# print(y.shape)
# X = StandardScaler().fit_transform(X)
# X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)X = np.linspace(1, 10, 10).reshape(-1, 1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05])# base_ht = DecisionTreeRegression(max_bins=10, max_depth=1)
base_ht = DecisionTreeRegressor(max_depth=1)
# n_estimators = np.linspace(2, 31, 29, dtype=np.int32)
# r2_scores = []
# for n in n_estimators:
# btr = BoostTreeRegressior(base_estimator=base_ht, n_estimators=n)
# btr.fit(X_train, y_train)
# y_hat = btr.predict(X_test)
# # print(r2_score(y_test, y_hat))
# r2_scores.append(r2_score(y_test, y_hat))
# print(n, ":", r2_scores[-1])r2_scores = []
for n in range(1, 7):btr = BoostTreeRegressor(base_estimator=base_ht, n_estimators=n)btr.fit(X, y)y_hat = btr.predict(X)# print(r2_score(y_test, y_hat))r2_scores.append(r2_score(y, y_hat))print(n, ":", r2_scores[-1], np.sum((y - y_hat) ** 2))# plt.figure(figsize=(7, 5))
# plt.plot(n_estimators, r2_scores, "ko-", lw=1)
# plt.show()# idx = np.argsort(y_test) # 對真值排序
#
# plt.figure(figsize=(7, 5))
# plt.plot(y_test[idx], "k-", lw=1.5, label="Test True")
# plt.plot(y_hat[idx], "r-", lw=1, label="Predict")
# plt.legend(frameon=False)
# plt.title("Regression Boosting Tree, R2 = %.5f, MSE = %.5f" %
# (r2_score(y_test, y_hat), ((y_test - y_hat) ** 2).mean()))
# plt.xlabel("Test Samples Serial Number", fontdict={"fontsize": 12})
# plt.ylabel("True VS Predict", fontdict={"fontsize": 12})
# plt.grid(ls=":")
#
# plt.show()

?2.5 梯度提升樹算法測試
test_gradboost_c1.py
from ch8.gradientboosting_c import GradientBoostClassifier
from sklearn.datasets import load_iris, load_digits, load_breast_cancer
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from ch4.decision_tree_R import DecisionTreeRegression
from sklearn.tree import DecisionTreeRegressor# iris = load_iris()
# X, y = iris.data, iris.targetdigits = load_digits()
X, y = digits.data, digits.target# bc_data = load_breast_cancer()
# X, y = bc_data.data, bc_data.targetX = PCA(n_components=10).fit_transform(X)
X = StandardScaler().fit_transform(X)X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=True, random_state=42)# base_es = DecisionTreeRegression(max_bins=50, max_depth=3)
base_es = DecisionTreeRegressor(max_depth=3)gbc = GradientBoostClassifier(base_estimator=base_es, n_estimators=50)
gbc.fit(X_train, y_train)
y_hat = gbc.predict(X_test)
print(classification_report(y_test, y_hat))
?三、Bagging算法
3.1 Bagging算法
bagging_c_r.py
import numpy as np
import copy
from ch4.decision_tree_R import DecisionTreeRegression # CART
from ch4.decision_tree_C import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, r2_scoreclass BaggingClassifierRegressor:"""1. Bagging的基本流程:采樣出T個含m個訓練樣本的采樣集,然后基于每個采樣集訓練出一個基學習器,再集成。2. 預測輸出進行結合:Bagging通常對分類任務采用簡單投票法,對回歸任務使用簡單平均法。3. 把回歸任務與分類任務集成到一個算法中,右參數task來控制,包外估計OOB控制"""def __init__(self, base_estimator=None, n_estimators=10, task="C", OOB=False):""":param base_estimator: 基學習器:param n_estimators: 基學習器的個數T:param task: 任務:C代表分類任務,R代表回歸任務:param OOB: 布爾變量,True表示進行包外估計"""self.base_estimator = base_estimatorself.n_estimators = n_estimatorsself.task = taskif task.lower() not in ["c", "r"]:raise ValueError("Bagging任務僅限分類(C/c)、回歸(R/r)")# 如果不提供基學習器,則默認按照深度為2的決策樹作為基分類器if self.base_estimator is None:if self.task.lower() == "c":self.base_estimator = DecisionTreeClassifier()elif self.task.lower() == "r":self.base_estimator = DecisionTreeRegression()if type(base_estimator) != list:# 同質(同種類型)的分類器,深拷貝self.base_estimator = [copy.deepcopy(self.base_estimator)for _ in range(self.n_estimators)]else:# 異質(不同種類型)的分類器self.n_estimators = len(self.base_estimator)self.OOB = OOB # 是否進行包外估計self.oob_indices = [] # 保存每次有放回采樣未被使用的樣本索引self.y_oob_hat = None # 包括估計樣本預測值(回歸)或預測類別概率(分類)self.oob_score = None # 包外估計的評分,分類和回歸def fit(self, x_train, y_train):"""Bagging算法(包含分類和回歸)的訓練:param x_train: 訓練集:param y_train: 目標集:return:"""x_train, y_train = np.asarray(x_train), np.asarray(y_train)n_samples = x_train.shape[0]for estimator in self.base_estimator:# 1. 有放回的隨機重采樣訓練集indices = np.random.choice(n_samples, n_samples, replace=True) # 采樣樣本索引indices = np.unique(indices)x_bootstrap, y_bootstrap = x_train[indices, :], y_train[indices]# 2. 基于采樣數據,訓練基學習器estimator.fit(x_bootstrap, y_bootstrap)# 存儲每個基學習器未使用的樣本索引n_indices = set(np.arange(n_samples)).difference(set(indices))self.oob_indices.append(list(n_indices)) # 每個基學習器未參與訓練的樣本索引# 3. 包外估計if self.OOB:if self.task.lower() == "c":self._oob_score_classifier(x_train, y_train)else:self._oob_score_regressor(x_train, y_train)def _oob_score_classifier(self, x_train, y_train):"""分類任務的包外估計:param x_train::param y_train::return:"""self.y_oob_hat, y_true = [], []for i in range(x_train.shape[0]): # 針對每個訓練樣本y_hat_i = [] # 當前樣本在每個基學習器下的預測概率,個數未必等于self.n_estimatorsfor idx in range(self.n_estimators): # 針對每個基學習器if i in self.oob_indices[idx]: # 如果該樣本屬于包外估計y_hat = self.base_estimator[idx].predict_proba(x_train[i, np.newaxis])y_hat_i.append(y_hat[0])# print(y_hat_i)if y_hat_i: # 非空,計算各基學習器預測類別概率的均值self.y_oob_hat.append(np.mean(np.c_[y_hat_i], axis=0))y_true.append(y_train[i]) # 存儲對應的真值self.y_oob_hat = np.asarray(self.y_oob_hat)self.oob_score = accuracy_score(y_true, np.argmax(self.y_oob_hat, axis=1))def _oob_score_regressor(self, x_train, y_train):"""回歸任務的包外估計:param x_train::param y_train::return:"""self.y_oob_hat, y_true = [], []for i in range(x_train.shape[0]): # 針對每個訓練樣本y_hat_i = [] # 當前樣本在每個基學習器下的預測概率,個數未必等于self.n_estimatorsfor idx in range(self.n_estimators): # 針對每個基學習器if i in self.oob_indices[idx]: # 如果該樣本屬于包外估計y_hat = self.base_estimator[idx].predict(x_train[i, np.newaxis])y_hat_i.append(y_hat[0])# print(y_hat_i)if y_hat_i: # 非空,計算各基學習器預測類別概率的均值self.y_oob_hat.append(np.mean(y_hat_i))y_true.append(y_train[i]) # 存儲對應的真值self.y_oob_hat = np.asarray(self.y_oob_hat)self.oob_score = r2_score(y_true, self.y_oob_hat)def predict_proba(self, x_test):"""分類任務中測試樣本所屬類別的概率預測:param x_test::return:"""if self.task.lower() != "c":raise ValueError("predict_proba()僅適用于分類任務。")x_test = np.asarray(x_test)y_test_hat = [] # 用于存儲測試樣本所屬類別概率for estimator in self.base_estimator:y_test_hat.append(estimator.predict_proba(x_test))# print(y_test_hat)return np.mean(y_test_hat, axis=0)def predict(self, x_test):"""分類任務:預測測試樣本所屬類別,類別概率大者索引為所屬類別回歸任務:預測測試樣本,對每個基學習器預測值簡單平均:param x_test::return:"""if self.task.lower() == "c":return np.argmax(self.predict_proba(x_test), axis=1)elif self.task.lower() == "r":y_hat = [] # 預測值for estimator in self.base_estimator:y_hat.append(estimator.predict(x_test))return np.mean(y_hat, axis=0)
3.2 Bagging算法測試
test_bagging_c1.py
from sklearn.datasets import load_iris
from ch8.bagging_c_r import BaggingClassifierRegressor
from ch4.decision_tree_C import DecisionTreeClassifier
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaleriris = load_iris()
X, y = iris.data, iris.target
X = StandardScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, shuffle=True, random_state=42)base_es = DecisionTreeClassifier(max_depth=10, max_bins=50, is_feature_all_R=True)
bagcr = BaggingClassifierRegressor(base_estimator=base_es, n_estimators=20, task="c", OOB=True)
bagcr.fit(X_train, y_train)
y_hat = bagcr.predict(X_test)
print(classification_report(y_test, y_hat))
print("包外估計的精度:", bagcr.oob_score)
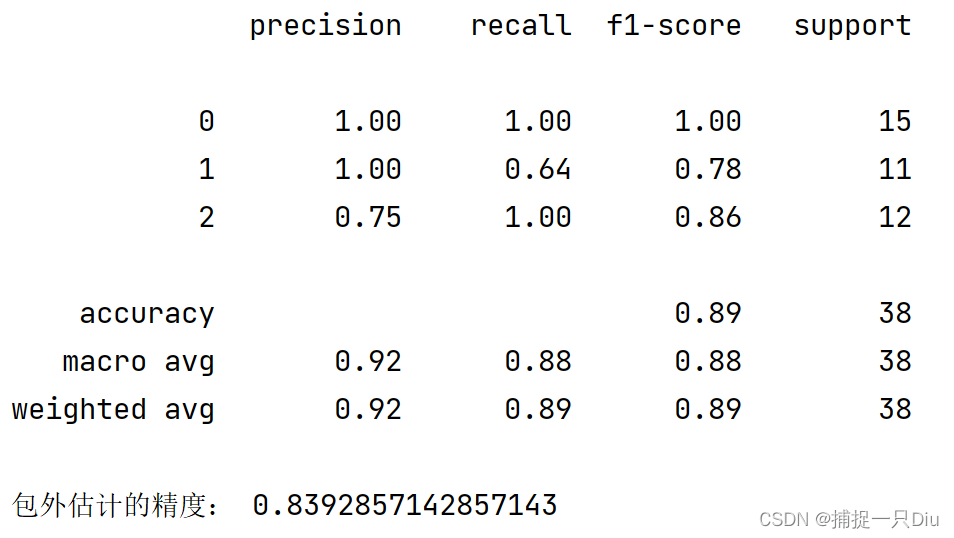
?test_bagging_c2.py
from sklearn.datasets import load_iris
from ch8.bagging_c_r import BaggingClassifierRegressor
from ch4.decision_tree_C import DecisionTreeClassifier
from sklearn.metrics import classification_report, accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, LabelEncoder
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltnursery = pd.read_csv("../ch4/data/nursery.csv").dropna()
X, y = np.asarray(nursery.iloc[:, :-1]), np.asarray(nursery.iloc[:, -1])
y = LabelEncoder().fit_transform(y)X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, shuffle=True, random_state=42)base_es = DecisionTreeClassifier(max_depth=10)
bagcr = BaggingClassifierRegressor(base_estimator=base_es, n_estimators=30, task="c")
bagcr.fit(X_train, y_train)
y_hat = bagcr.predict(X_test)
print(classification_report(y_test, y_hat))
# print("包外估計的精度:", bagcr.oob_score)y_test_scores = []
for i in range(30):bagcr = BaggingClassifierRegressor(base_estimator=base_es, n_estimators=1, task="c")bagcr.fit(X_train, y_train)y_hat = bagcr.predict(X_test)y_test_scores.append(accuracy_score(y_test, y_hat))plt.figure(figsize=(7, 5))
plt.plot(range(1, 31), y_test_scores, "ko-", lw=1.5)
plt.xlabel("Training Times", fontsize=12)
plt.ylabel("Test Accuracy", fontsize=12)
plt.grid(ls=":")
plt.show()?test_bagging_r.py
import numpy as np
import matplotlib.pyplot as plt
from ch4.decision_tree_R import DecisionTreeRegression
from ch8.bagging_c_r import BaggingClassifierRegressor
from sklearn.metrics import r2_scoref = lambda x: 0.5 * np.exp(-(x + 3) ** 2) + np.exp(-x ** 2) + 1.5 * np.exp(-(x - 3) ** 2)np.random.seed(0)
N = 200
X = np.random.rand(N) * 10 - 5
X = np.sort(X)
y = f(X) + 0.05 * np.random.randn(N)
X = X.reshape(-1, 1)
# print(X)base_estimator = DecisionTreeRegression(max_bins=30, max_depth=8)
model = BaggingClassifierRegressor(base_estimator=base_estimator, n_estimators=100, task="r")
model.fit(X, y)X_test = np.linspace(1.1 * X.min(axis=0), 1.1 * X.max(axis=0), 1000).reshape(-1, 1)y_bagging_hat = model.predict(X_test)base_estimator.fit(X, y)
y_cart_hat = base_estimator.predict(X_test)plt.figure(figsize=(7, 5))
plt.scatter(X, y, s=10, c="k", label="Raw Data")
plt.plot(X_test, f(X_test), "k-", lw=1.5, label="True F(x)")
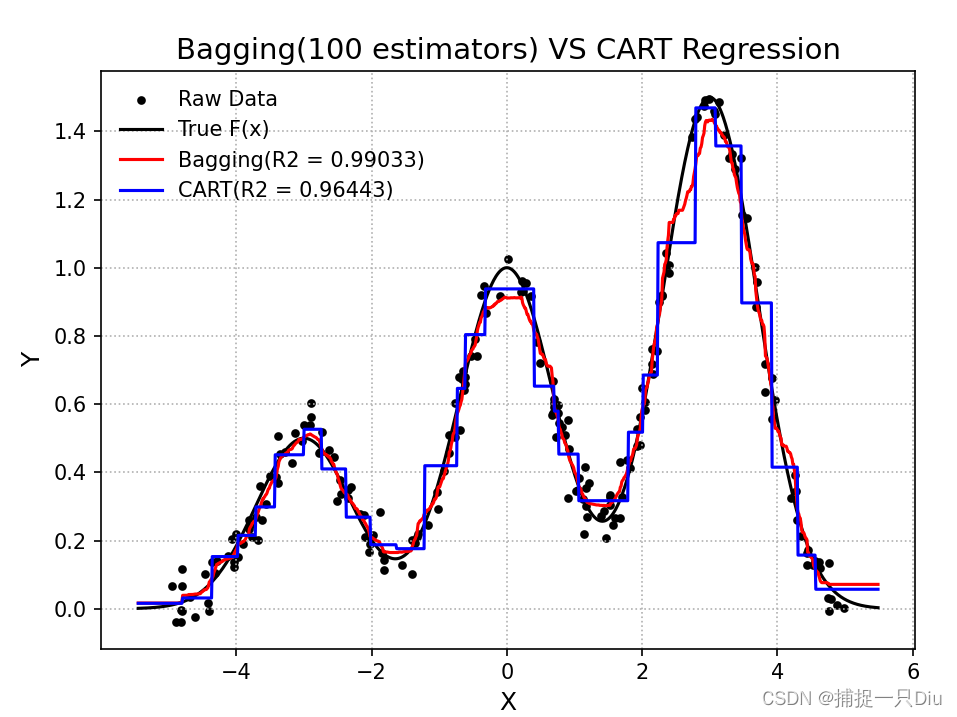
plt.plot(X_test, y_bagging_hat, "r-", label="Bagging(R2 = %.5f)" % r2_score(f(X_test), y_bagging_hat))
plt.plot(X_test, y_cart_hat, "b-", label="CART(R2 = %.5f)" % r2_score(f(X_test), y_cart_hat))
plt.legend(frameon=False)
plt.xlabel("X", fontsize=12)
plt.ylabel("Y", fontsize=12)
plt.grid(ls=":")
plt.title("Bagging(100 estimators) VS CART Regression", fontsize=14)
plt.show()
四、隨機森林算法
4.1 隨機森林算法
?rf_classifier_regressor.py
import numpy as np
import copy
from ch4.decision_tree_R import DecisionTreeRegression # CART
from ch4.decision_tree_C import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, r2_scoreclass RandomForestClassifierRegressor:"""隨機森林RF是Bagging的一個擴展變體。 RF在以決策樹為基學習器構建Bagging集成的基礎上,進一步在決策樹的訓練過程中引入了隨機屬性選擇, 即對訓練樣本和輸入變量增加隨機擾動。"""def __init__(self, base_estimator=None, n_estimators=10, feature_sampling_rate=0.5,task="C", OOB=False, feature_importance=False):""":param base_estimator: 基學習器:param n_estimators: 基學習器的個數T:param task: 任務:C代表分類任務,R代表回歸任務:param OOB: 布爾變量,True表示進行包外估計:param feature_sampling_rate: 特征變量的抽樣率:param feature_importance: 布爾變量,表示是否進行特征重要性的評估"""self.base_estimator = base_estimatorself.n_estimators = n_estimatorsself.feature_sampling_rate = feature_sampling_rateif task.lower() not in ["c", "r"]:raise ValueError("Bagging任務僅限分類(C/c)、回歸(R/r)")self.task = task# 如果不提供基學習器,則默認決策樹作為基分類器if self.base_estimator is None:if self.task.lower() == "c":base_estimator = DecisionTreeClassifier()elif self.task.lower() == "r":base_estimator = DecisionTreeRegression()self.base_estimator = [copy.deepcopy(base_estimator)for _ in range(self.n_estimators)]self.OOB = OOB # 是否進行包外估計self.oob_indices = [] # 保存每次有放回采樣未被使用的樣本索引self.y_oob_hat = None # 包括估計樣本預測值(回歸)或預測類別概率(分類)self.oob_score = None # 包外估計的評分,分類和回歸self.feature_importance = feature_importanceself.feature_importance_scores = None # 特征變量的重要性評分self.feature_importance_indices = [] # 針對每個基學習器,存儲特征變量的抽樣索引def fit(self, x_train, y_train):"""隨機森林算法(包含分類和回歸)的訓練:param x_train: 訓練集:param y_train: 目標集:return:"""x_train, y_train = np.asarray(x_train), np.asarray(y_train)n_samples, n_features = x_train.shapefor estimator in self.base_estimator:# 1. 有放回的隨機重采樣訓練集indices = np.random.choice(n_samples, n_samples, replace=True) # 采樣樣本索引indices = np.unique(indices)x_bootstrap, y_bootstrap = x_train[indices, :], y_train[indices]# 2. 對特征屬性變量進行抽樣fb_num = int(self.feature_sampling_rate * n_features) # 抽樣特征數feature_idx = np.random.choice(n_features, fb_num, replace=False) # 不放回self.feature_importance_indices.append(feature_idx)x_bootstrap = x_bootstrap[:, feature_idx] # 獲取特征變量抽樣后的訓練樣本# 3. 基于采樣數據,訓練基學習器estimator.fit(x_bootstrap, y_bootstrap)# 存儲每個基學習器未使用的樣本索引n_indices = set(np.arange(n_samples)).difference(set(indices))self.oob_indices.append(list(n_indices)) # 每個基學習器未參與訓練的樣本索引# 4. 包外估計if self.OOB:if self.task.lower() == "c":self._oob_score_classifier(x_train, y_train)else:self._oob_score_regressor(x_train, y_train)# 5. 特征重要性估計if self.feature_importance:if self.task.lower() == "c":self._feature_importance_score_classifier(x_train, y_train)else:self._feature_importance_score_regressor(x_train, y_train)def _oob_score_classifier(self, x_train, y_train):"""分類任務的包外估計:param x_train::param y_train::return:"""self.y_oob_hat, y_true = [], []for i in range(x_train.shape[0]): # 針對每個訓練樣本y_hat_i = [] # 當前樣本在每個基學習器下的預測概率,個數未必等于self.n_estimatorsfor idx in range(self.n_estimators): # 針對每個基學習器if i in self.oob_indices[idx]: # 如果該樣本屬于包外估計x_sample = x_train[i, self.feature_importance_indices[idx]]y_hat = self.base_estimator[idx].predict_proba(x_sample.reshape(1, -1))y_hat_i.append(y_hat[0])# print(y_hat_i)if y_hat_i: # 非空,計算各基學習器預測類別概率的均值self.y_oob_hat.append(np.mean(np.c_[y_hat_i], axis=0))y_true.append(y_train[i]) # 存儲對應的真值self.y_oob_hat = np.asarray(self.y_oob_hat)self.oob_score = accuracy_score(y_true, np.argmax(self.y_oob_hat, axis=1))def _oob_score_regressor(self, x_train, y_train):"""回歸任務的包外估計:param x_train::param y_train::return:"""self.y_oob_hat, y_true = [], []for i in range(x_train.shape[0]): # 針對每個訓練樣本y_hat_i = [] # 當前樣本在每個基學習器下的預測概率,個數未必等于self.n_estimatorsfor idx in range(self.n_estimators): # 針對每個基學習器if i in self.oob_indices[idx]: # 如果該樣本屬于包外估計x_sample = x_train[i, self.feature_importance_indices[idx]]y_hat = self.base_estimator[idx].predict(x_sample.reshape(1, -1))y_hat_i.append(y_hat[0])# print(y_hat_i)if y_hat_i: # 非空,計算各基學習器預測類別概率的均值self.y_oob_hat.append(np.mean(y_hat_i))y_true.append(y_train[i]) # 存儲對應的真值self.y_oob_hat = np.asarray(self.y_oob_hat)self.oob_score = r2_score(y_true, self.y_oob_hat)def _feature_importance_score_classifier(self, x_train, y_train):"""分類問題的特征變量重要性評估計算:param x_train::param y_train::return:"""n_feature = x_train.shape[1]self.feature_importance_scores = np.zeros(n_feature) # 特征變量重要性評分for f_j in range(n_feature): # 針對每個特征變量f_j_scores = [] # 當前第j個特征變量在所有基學習器預測的OOB誤差變化for idx, estimator in enumerate(self.base_estimator):f_s_indices = list(self.feature_importance_indices[idx]) # 獲取當前基學習器的特征變量索引if f_j in f_s_indices: # 表示當前基學習器中存在第j個特征變量# 1. 計算基于OOB的測試誤差errorx_samples = x_train[self.oob_indices[idx], :][:, f_s_indices] # OOB樣本以及特征抽樣y_hat = estimator.predict(x_samples)error = 1 - accuracy_score(y_train[self.oob_indices[idx]], y_hat)# 2. 計算第j個特征隨機打亂順序后的測試誤差np.random.shuffle(x_samples[:, f_s_indices.index(f_j)]) # 原地打亂第j個特征變量取值,其他特征取值不變y_hat_j = estimator.predict(x_samples)error_j = 1 - accuracy_score(y_train[self.oob_indices[idx]], y_hat_j)f_j_scores.append(error_j - error)# 3. 計算所有基學習器對當前第j個特征評分的均值self.feature_importance_scores[f_j] = np.mean(f_j_scores)return self.feature_importance_scoresdef _feature_importance_score_regressor(self, x_train, y_train):"""回歸任務的特征變量重要性評估計算:param x_train::param y_train::return:"""n_feature = x_train.shape[1]self.feature_importance_scores = np.zeros(n_feature) # 特征變量重要性評分for f_j in range(n_feature): # 針對每個特征變量f_j_scores = [] # 當前第j個特征變量在所有基學習器預測的OOB誤差變化for idx, estimator in enumerate(self.base_estimator):f_s_indices = list(self.feature_importance_indices[idx]) # 獲取當前基學習器的特征變量索引if f_j in f_s_indices: # 表示當前基學習器中存在第j個特征變量# 1. 計算基于OOB的測試誤差errorx_samples = x_train[self.oob_indices[idx], :][:, f_s_indices] # OOB樣本以及特征抽樣y_hat = estimator.predict[x_samples]error = 1 - r2_score(y_train[self.oob_indices[idx]], y_hat)# 2. 計算第j個特征隨機打亂順序后的測試誤差np.random.shuffle(x_samples[:, f_s_indices.index(f_j)]) # 原地打亂第j個特征變量取值,其他特征取值不變y_hat_j = estimator.predict[x_samples]error_j = 1 - r2_score(y_train[self.oob_indices[idx]], y_hat_j)f_j_scores.append(error_j - error)# 3. 計算所有基學習器對當前第j個特征評分的均值self.feature_importance_scores[f_j] = np.mean(f_j_scores)return self.feature_importance_scoresdef predict_proba(self, x_test):"""分類任務中測試樣本所屬類別的概率預測:param x_test::return:"""if self.task.lower() != "c":raise ValueError("predict_proba()僅適用于分類任務。")x_test = np.asarray(x_test)y_test_hat = [] # 用于存儲測試樣本所屬類別概率for idx, estimator in enumerate(self.base_estimator):x_test_bootstrap = x_test[:, self.feature_importance_indices[idx]]y_test_hat.append(estimator.predict_proba(x_test_bootstrap))# print(y_test_hat)return np.mean(y_test_hat, axis=0)def predict(self, x_test):"""分類任務:預測測試樣本所屬類別,類別概率大者索引為所屬類別回歸任務:預測測試樣本,對每個基學習器預測值簡單平均:param x_test::return:"""if self.task.lower() == "c":return np.argmax(self.predict_proba(x_test), axis=1)elif self.task.lower() == "r":y_hat = [] # 預測值for idx, estimator in enumerate(self.base_estimator):x_test_bootstrap = x_test[:, self.feature_importance_indices[idx]]y_hat.append(estimator.predict(x_test_bootstrap))return np.mean(y_hat, axis=0)
?4.2 隨機森林算法測試
test_rf_c1.py
?
from sklearn.datasets import load_iris, load_wine, load_digits
from ch8.randomforest.rf_classifier_regressor import RandomForestClassifierRegressor
# from ch4.decision_tree_C import DecisionTreeClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pdiris = load_iris()
X, y = iris.data, iris.target
X = StandardScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, shuffle=True, random_state=42)# base_es = DecisionTreeClassifier(max_depth=10, max_bins=50, is_feature_all_R=True)
base_es = DecisionTreeClassifier(max_depth=10)
rf_model = RandomForestClassifierRegressor(base_estimator=base_es, n_estimators=30,task="c", OOB=True, feature_importance=True)
rf_model.fit(X_train, y_train)
y_hat = rf_model.predict(X_test)
print(classification_report(y_test, y_hat))
print("包外估計的精度:", rf_model.oob_score)
print("特征重要性評分:", rf_model.feature_importance_scores)plt.figure(figsize=(9, 5))
data_pd = pd.DataFrame([iris.feature_names, rf_model.feature_importance_scores]).T
data_pd.columns = ["Feature Names", "Importance"]
sns.barplot(x="Importance", y="Feature Names", data=data_pd)
plt.title("Iris DataSet Feature Importance Scores", fontdict={"fontsize": 14})
plt.grid(ls=":")
print(data_pd)
plt.show()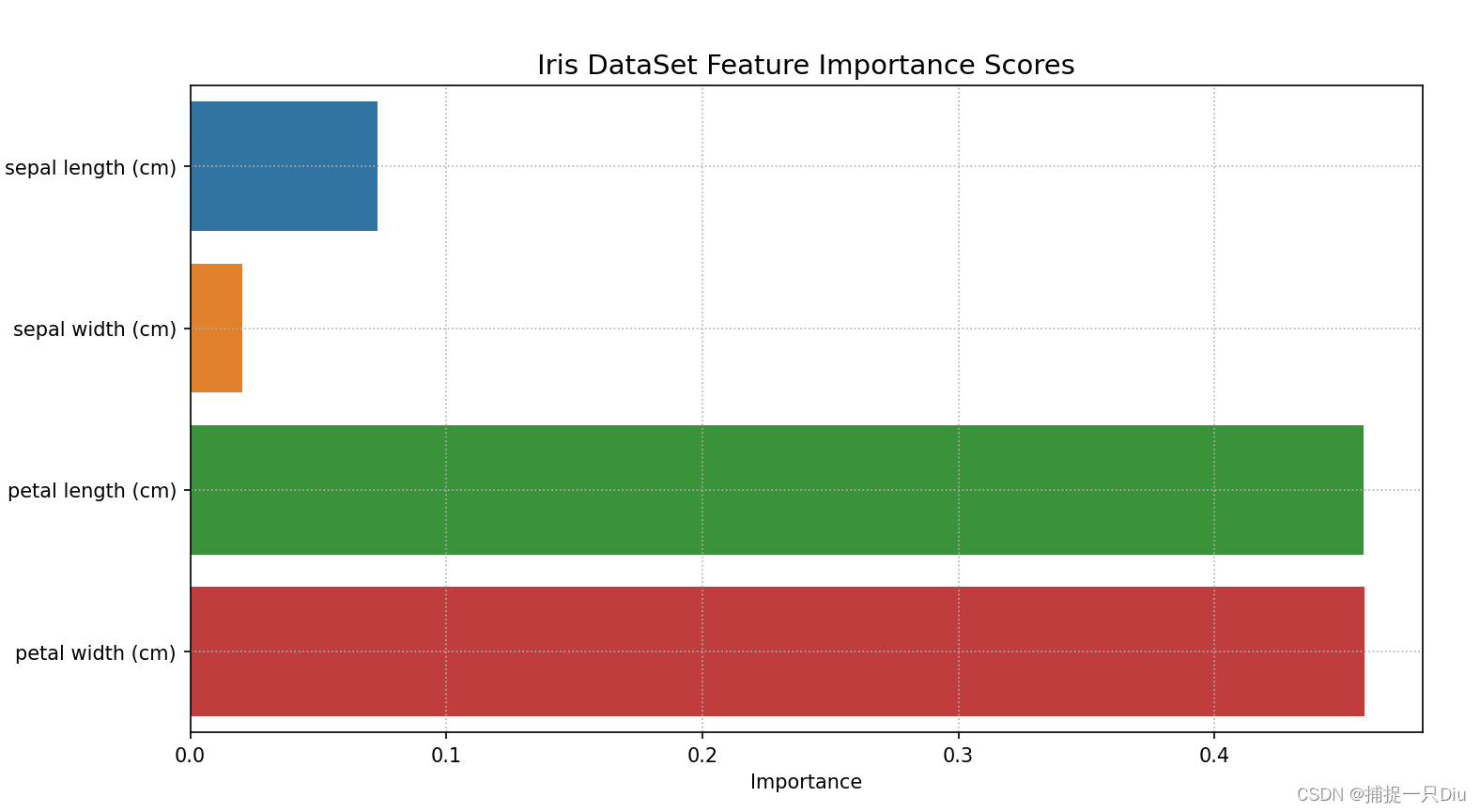
?

)








)


KMP)



)
 3DSlicer的醫學圖像數據增強擴展模塊)
)