【C++從0到王者】第四十八站：最短路徑

文章目錄

  • 一、最短路徑
  • 二、單源最短路徑 -- Dijkstra算法
    • 1.單源最短路徑問題
    • 2.算法思想
    • 3.代碼實現
    • 4.負權值帶來的問題
  • 三、單源最短路徑 -- Bellman-Ford算法
    • 1.算法思想
    • 2.算法實現
    • 3.SPFA優化
    • 4.負權回路
  • 四、多源最短路徑 -- Floyd-Warshall算法
    • 1.算法思想
    • 2.算法實現

一、最短路徑

最短路徑問題：從在帶權有向圖G中的某一頂點出發，找出一條通往另一頂點的最短路徑，最短也就是沿路徑各邊的權值總和達到最小。

一般來說，最短路徑都是針對于有向圖的，但是對于無向圖也是可以的！

二、單源最短路徑 – Dijkstra算法

1.單源最短路徑問題

單源最短路徑問題：給定一個圖G = ( V ， E ) ，求源結點s ∈ V到圖中每個結點v ∈ V的最短路徑。Dijkstra算法就適用于解決帶權重的有向圖上的單源最短路徑問題，同時算法要求圖中所有邊的權重非負。一般在求解最短路徑的時候都是已知一個起點和一個終點，所以使用Dijkstra算法求解過后也就得到了所需起點到終點的最短路徑。

2.算法思想

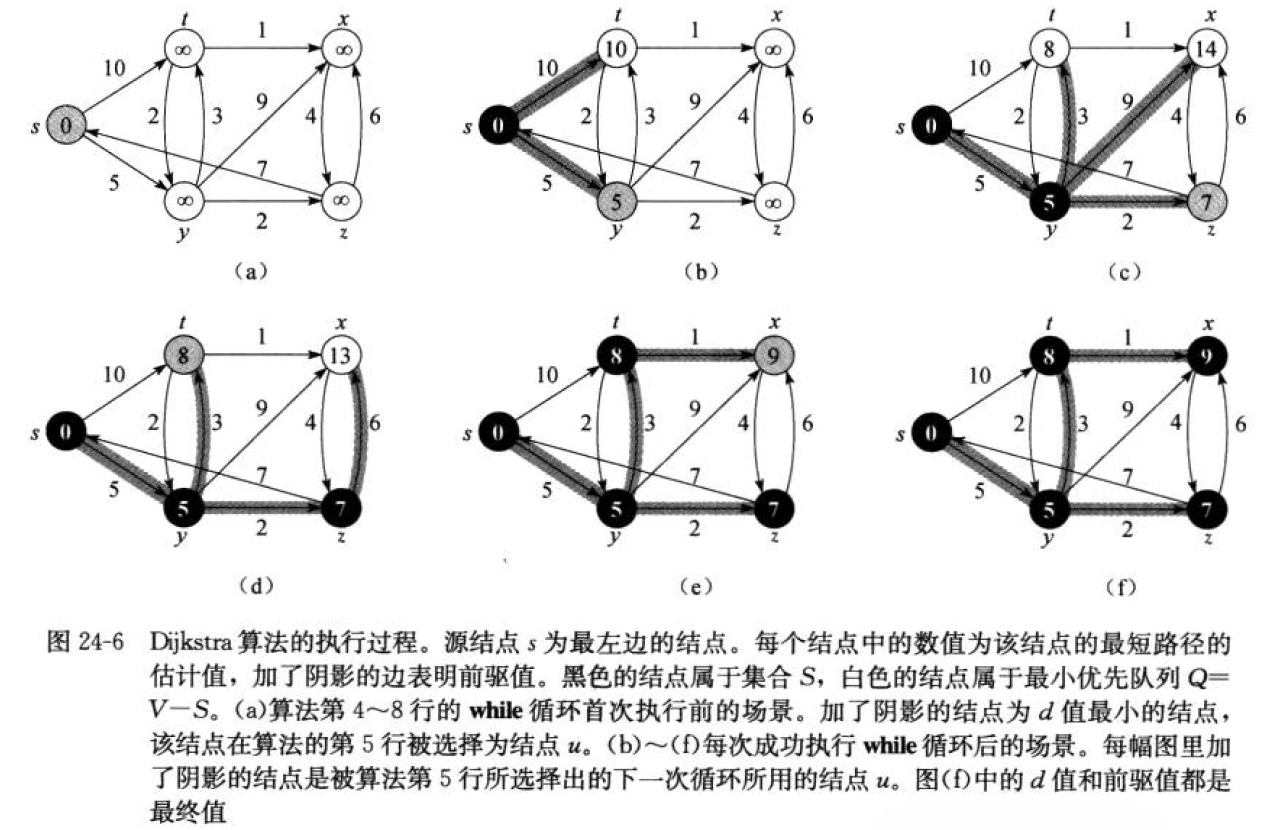
針對一個帶權有向圖G，將所有結點分為兩組S和Q，S是已經確定最短路徑的結點集合，在初始時為空（初始時就可以將源節點s放入，畢竟源節點到自己的代價是0），Q 為其余未確定最短路徑的結點集合，每次從Q 中找出一個起點到該結點代價最小的結點u ，將u 從Q 中移出，并放入S中，對u 的每一個相鄰結點v進行松弛操作。松弛即對每一個相鄰結點v ，判斷源節點s到結點u的代價與u 到v 的代價之和是否比原來s 到v 的代價更小，若代價比原來小則要將s 到v 的代價更新為s 到u 與u 到v 的代價之和，否則維持原樣。如此一直循環直至集合Q 為空，即所有節點都已經查找過一遍并確定了最短路徑，至于一些起點到達不了的結點在算法循環后其代價仍為初始設定的值，不發生變化。Dijkstra算法每次都是選擇V-S中最小的路徑節點來進行更新，并加入S中，所以該算法使用的是貪心策略

注意:Dijkstra算法存在的問題是不支持圖中帶負權路徑，如果帶有負權路徑，則可能會找不到一些路徑的最短路徑。

image-20240222011135364

3.代碼實現

namespace matrix
{//V代表頂點， W是weight代表權值，MAX_W代表權值的最大值，Direction代表是有向圖還是無向圖,flase表示無向template<class V, class W, W Max_W = INT_MAX, bool Direction = false>class Graph{typedef Graph<V, W, Max_W, Direction> Self;public:Graph() = default;//圖的創建//1. IO輸入 不方便測試//2. 圖結構關系寫到文件，讀取文件//3. 手動添加邊Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; i++){_vertexs.push_back(a[i]);_indexMap[a[i]] = i;}_matrix.resize(n);for (size_t i = 0; i < _matrix.size(); i++){_matrix[i].resize(n, Max_W);}}size_t GetVertexIndex(const V& v){//return _indexMap[v];auto it = _indexMap.find(v);if (it != _indexMap.end()){return it->second;}else{//assert(false)throw invalid_argument("頂點不存在");return -1;}}void _AddEdge(size_t srci, size_t dsti, const W& w){_matrix[srci][dsti] = w;if (Direction == false){_matrix[dsti][srci] = w;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVertexIndex(src);size_t dsti = GetVertexIndex(dst);_AddEdge(srci, dsti, w);}void Print(){for (size_t i = 0; i < _vertexs.size(); i++){cout << "[" << i << "]" << "->" << _vertexs[i] << endl;}cout << endl;cout << "   ";for (int i = 0; i < _vertexs.size(); i++){//cout << _vertexs[i] << " ";printf("%-3d ", i);}cout << endl;for (size_t i = 0; i < _matrix.size(); i++){//cout << _vertexs[i] << " ";printf("%d ", i);for (size_t j = 0; j < _matrix[i].size(); j++){if (_matrix[i][j] == INT_MAX){cout << " *  ";}else{printf(" %d  ", _matrix[i][j]);//cout << _matrix[i][j] << " ";}}cout << endl;}for (size_t i = 0; i < _matrix.size(); i++){for (size_t j = 0; j < _matrix[i].size(); j++){if (i < j && _matrix[i][j] != Max_W){cout << _vertexs[i] << "->" << _vertexs[j] << ":" << _matrix[i][j] << endl;}}}}void BFS(const V& src){int srci = GetVertexIndex(src);queue<int> q; //廣度遍歷的隊列vector<bool> visited(_vertexs.size(), false); //標記數組q.push(srci); //起點入隊visited[srci] = true; //已經被遍歷過了while (!q.empty()){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << endl;//把front頂點的鄰接頂點入隊列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}} void BFSLevel(const V& src){int srci = GetVertexIndex(src);queue<int> q; //廣度遍歷的隊列vector<bool> visited(_vertexs.size(), false); //標記數組q.push(srci); //起點入隊visited[srci] = true; //已經被遍歷過了int levelSize = 1;while (!q.empty()){for (int i = 0; i < levelSize; i++){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << " ";//把front頂點的鄰接頂點入隊列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}cout << endl;levelSize = q.size();}}void _DFS(size_t srci, vector<bool>& visited){cout << srci << ":" << _vertexs[srci] << endl;visited[srci] = true;for (int i = 0; i < _matrix[srci].size(); i++){if (_matrix[srci][i] != Max_W && visited[i] == false){_DFS(i, visited);}}}void DFS(const V& src){int srci = GetVertexIndex(src);vector<bool> visited(_vertexs.size(), false);_DFS(srci, visited);}struct Edge{int _srci;int _dsti;W _w;Edge(int srci, int dsti, W w):_srci(srci),_dsti(dsti),_w(w){}bool operator>(const Edge& e) const{return this->_w > e._w;}};//傳入的是一個只有結點的，沒有邊的圖W Kruskal(Self& minTree){//先將所有的邊，按照小堆的方式進行組織起來priority_queue<Edge, vector<Edge>, greater<Edge>> minque;size_t n = _vertexs.size();for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){//由于這里是無向圖，他是一個對稱矩陣，但是我們的邊只考慮一半就已經可以了。剩下的就重復了。if (i < j && _matrix[i][j] != Max_W){//已經按照自身的，帶有邊的圖，將所有的邊的信息全部組織好了minque.push(Edge(i, j, _matrix[i][j]));}}}//因為最小生成樹一定是n-1條邊，所以我們現在要選出n-1條邊，size是計數器int size = 0;//用于計算權值W totalW = W();//最關鍵的問題是判環，這里我們可以用并查集去檢測是否這兩個頂點在一個集合里面，如果在集合里面，說明一定是連通的，在加上就成環了UnionFindSet ufs(n);//開始選邊，我們要考慮到所有的邊while (!minque.empty()){//取出一個最小的邊，然后就可以將他踢出優先級隊列了，如果被選中不需要它了，如果沒有被選中，那只能是因為出現環了才不要它了。Edge min = minque.top();minque.pop();//看看是否在一個集合里面，如果在一個集合里面，那么他們已經是連通了，沒必要在連通，還想要連通那么一定是環！if (!ufs.InSet(min._srci, min._dsti)){//我們可以看看我們選出來的邊cout << _vertexs[min._srci] << "-" << _vertexs[min._dsti] << ":" << min._w << endl;//該邊是符合的，我們直接為這個圖加上邊minTree._AddEdge(min._srci, min._dsti, min._w);//加上之后，就連通了，我們讓他們形成集合ufs.Union(min._srci, min._dsti);//我們一定只有n-1條邊，我們需要計數++size;//將總的權值要加起來totalW += min._w;}//成環的情況，我們只是看看這是哪條邊else{cout << "構成環啦！:";cout << _vertexs[min._srci] << "-" << _vertexs[min._dsti] << ":" << min._w << endl;}}//上面的循環中，如果圖是連通的，那么最終一定選出來的是n-1條邊。除非圖是不連通的。if (size == n - 1){return totalW;}//圖不連通，直接返回0else{return W();}}W Prim(Self& minTree, const V& src){size_t srci = GetVertexIndex(src);int n = _vertexs.size();//使用集合的方式//set<int> X;//set<int> Y;//X.insert(srci);//for (int i = 0; i < n; i++)//{//	if (i != srci)//	{//		Y.insert(i);//	}//}//利用vector的方式,去記錄兩個集合。vector<bool> X(n, false);vector<bool> Y(n, true);X[srci] = true;Y[srci] = false;//從X->Y集合中連接的邊去選最小的邊priority_queue<Edge, vector<Edge>, greater<Edge>> minq;//把目前為止X集合（僅僅只有起點）的相關的邊，全部放入優先級隊列中for (int i = 0; i < n; i++){if (_matrix[srci][i] != Max_W){minq.push(Edge(srci, i, _matrix[srci][i]));}}//size用來判斷是否達到最小生成樹的個數n-1,totalW用來計算權值之和size_t size = 0;W totalW = W();//我們開始在優先級隊列中去尋找while (!minq.empty()){//在優先級隊列中找到一個最小的元素，由于優先級隊列中的一定是我們X集合可以延申的邊。所以是滿足Prim的選邊條件的Edge min = minq.top();//如果邊使用了，那么就不用了，如果不使用，那肯定是因為環才導致的，那也不要了minq.pop();//這里比較巧妙，因為根據我們的算法思想，我們選邊的時候一定是從X集合的某一個頂點開始的，然后去找一個不在X集合里面的頂點//所以這里我們可以直接判斷目的點是否在X集合里面，如果在，那么一定是環。如果不是，才可以把這條邊給加上去if (X[min._dsti]){//cout << "構成環：";//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;continue;}//把邊給加上去minTree._AddEdge(min._srci, min._dsti, min._w);//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;//X.insert(min._dsti);//Y.erase(min._dsti);//處理一下目的點的邊X[min._dsti] = true;Y[min._dsti] = false;++size;totalW += min._w;//這里相當于一次優化，因為該循環一定可以保證選出來的n-1條邊是最小生成樹，//后面的優先級隊列中的任何一條邊一定會導致出現環，會在前面的檢測目的點是否在X集合中被處理掉。//這里則是直接不用繼續入其他的邊進入隊列了。可以提高一些效率，減少無用的操作if (size == n - 1){break;}//當一條邊添加完成后，它就屬于X集合了，我們可以將該點所延申出的邊給加入到優先級隊列中//只有該邊存在，且目的地沒有被加入過的時候，才會入隊列。值得耐人尋味的是，這里雖然已經處理過一次可能出現環的情況了//但是可能由于在添加邊的時候，導致某些優先級隊列中的邊會導致構成環了，所以就有了前面的再次根據目的地時候在X集合中去判環for (int i = 0; i < n; i++){if (_matrix[min._dsti][i] != Max_W && X[i] == false){minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));}}}if (size == n - 1){return totalW;}else{return W();}}void PrintShortPath(const V& src, const vector<W>& dist, const vector<int>& pPath){size_t srci = GetVertexIndex(src);int n = _vertexs.size();for (int i = 0; i < n; i++){if (i != srci){cout << "[" << "pathlenth:" << dist[i] << "]";stack<int> path;size_t parent = i;while (parent != srci){path.push(parent);parent = pPath[parent];}path.push(parent);cout << "path:";while (!path.empty()){ int top = path.top();path.pop();cout << _vertexs[top] << "->";}cout << "nullptr" << endl;}}}//src是起始結點，dist數組的內容是存放最短路徑值的權值，即每個元素的內容代表著從起始結點到該結點的最短路徑//pPath數組是路徑的數組，因為有時候我們需要求出路徑的具體走法，所以我們可以用數組的方式，類似于并查集去尋找路徑的方式，建立一顆樹void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath){//確定好起始結點的下標size_t srci = GetVertexIndex(src);int n = _vertexs.size();//我們先讓所有的最短路徑無窮。即還未求出來dist.resize(n, Max_W);//注意源節點到源節點的最短路徑一定是0dist[srci] = 0;//我們讓所有的路徑都設置為-1，意味著所有的結點都沒有找出來最短路徑pPath.resize(n, -1);//這是表示起點它的路徑就是它自己，這步其實只是為了讓起點和為求出最短路徑給分開表示。不然都用-1可能會混亂pPath[srci] = srci;//這個S集合代表我們已經求出最短路徑的集合。如果是true代表著這個結點早已求出了最短路徑。false代表未求出vector<bool> S(n, false);//注意這里我們做一下特殊處理，雖然我們起點它本來就應該放在這個集合里面，但是我們還是先讓它為false。這里我們其實是想與下面的循環進行合并//所以迫不得已做的操作，因為一旦將某個結點設置為true，那么它的相鄰的結點路徑也應該被更新一下，那么這里就要把下面的對于代碼拷貝一份。//所以為了讓代碼簡潔，我們直接不寫這一步了，和下面的進行合并//S[srci] = true;//這里只是控制一下循環次數，因為我們要求所有的結點都要被遍歷一下，而每次只會遍歷一個結點，即將一個結點給放入S集合。//我們每次點亮的一定是之前從未遍歷過的結點for(int j = 0; j < n; j++){//Dijkstra算法要求每次都要找出一個，還沒有被訪問過的（不在S集合的），并且是有路徑的，且路徑是當前最小的一個結點//對于第一次找到的就是srci以及所對應的0值int u = 0;W min = Max_W;for (int i = 0; i < n; i++){if (S[i] == false && dist[i] < min){u = i;min = dist[i];}}//找到以后，我們可以讓他加入S集合，代表它已經被訪問過了。借助這里找到了srci，并且使他加入到S集合S[u] = true;//松弛更新u連接頂點v， srci->u + u->v < srci->v 就更新//注意，這里我們需要的是找到我們新加入S集合的鄰接的頂點，然后判斷是不是需要更新最短路徑，//但是我們一開始并不知道，所以我們遍歷所有的結點，依次判斷條件是否滿足for (int v = 0; v < n; v++){//我們這個要更新的不能是我們之前已經訪問過的了。因為之前訪問過的一定是最短路徑了！if (S[v] == false &&//因為是要鄰接的頂點，它必須要直接連通的兩個頂點。所以用這個條件進行排除_matrix[u][v] != Max_W//這是為了看一看用這個算出來的是不是小于我們原來的路徑，如果是，那么最短路徑就變成它了&& dist[u] + _matrix[u][v] < dist[v]){//更新最短路徑dist[v] = dist[u] + _matrix[u][v];//更新路徑的樹pPath[v] = u;}}}}private:vector<V> _vertexs; //頂點集合map<V, int> _indexMap; //頂點對應的下標關系vector<vector<W>> _matrix; //臨界矩陣};void TestGraphDijkstra(){const char* str = "syztx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 10);g.AddEdge('s', 'y', 5);g.AddEdge('y', 't', 3);g.AddEdge('y', 'x', 9);g.AddEdge('y', 'z', 2);g.AddEdge('z', 's', 7);g.AddEdge('z', 'x', 6);g.AddEdge('t', 'y', 2);g.AddEdge('t', 'x', 1);g.AddEdge('x', 'z', 4);vector<int> dist;vector<int> parentPath;g.Dijkstra('s', dist, parentPath);g.PrintShortPath('s', dist, parentPath);}void TestGraph(){Graph<char, int, INT_MAX, true> g("0123", 4);g.AddEdge('0', '1', 1);g.AddEdge('0', '3', 4);g.AddEdge('1', '3', 2);g.AddEdge('1', '2', 9);g.AddEdge('2', '3', 8);g.AddEdge('2', '1', 5);g.AddEdge('2', '0', 3);g.AddEdge('3', '2', 6);g.Print();}void TestGraphBDFS(){string a[] = { "張三", "李四", "王五", "趙六", "周七" };Graph<string, int> g1(a, sizeof(a) / sizeof(string));g1.AddEdge("張三", "李四", 100);g1.AddEdge("張三", "王五", 200);g1.AddEdge("王五", "趙六", 30);g1.AddEdge("王五", "周七", 30);g1.Print();g1.BFS("張三");cout << endl;g1.BFSLevel("張三");cout << endl;g1.DFS("張三");}void TestGraphMinTree(){const char* str = "abcdefghi";Graph<char, int> g(str, strlen(str));g.AddEdge('a', 'b', 4);g.AddEdge('a', 'h', 8);//g.AddEdge('a', 'h', 9);g.AddEdge('b', 'c', 8);g.AddEdge('b', 'h', 11); g.AddEdge('c', 'i', 2);g.AddEdge('c', 'f', 4);g.AddEdge('c', 'd', 7);g.AddEdge('d', 'f', 14);g.AddEdge('d', 'e', 9);g.AddEdge('e', 'f', 10);g.AddEdge('f', 'g', 2);g.AddEdge('g', 'h', 1);g.AddEdge('g', 'i', 6);g.AddEdge('h', 'i', 7);//Graph<char, int> kminTree;//Graph<char, int> kminTree(str, strlen(str));//cout << "Kruskal:" << g.Kruskal(kminTree) << endl;//kminTree.Print();//Graph<char, int> pminTree(str, strlen(str));//cout << "Prim:" << g.Prim(pminTree, 'a') << endl;//pminTree.Print();for (int i = 0; i < strlen(str); i++){Graph<char, int> pminTree(str, strlen(str));cout << "Prim:" << str[i] << ":" << g.Prim(pminTree, str[i]) << endl;}}
}

運行結果如下

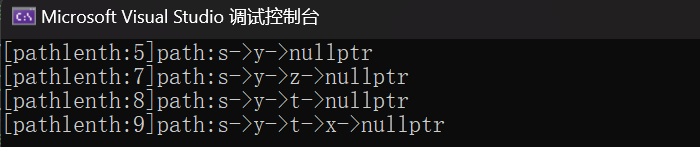
image-20240222013452523

上面的算法具體解釋已經放在了注釋當中,我們將代碼單獨拉出來方便我們閱讀

注意的是,已經訪問過的結點,一定不能再次訪問了!

		//src是起始結點，dist數組的內容是存放最短路徑值的權值，即每個元素的內容代表著從起始結點到該結點的最短路徑//pPath數組是路徑的數組，因為有時候我們需要求出路徑的具體走法，所以我們可以用數組的方式，類似于并查集去尋找路徑的方式，建立一顆樹void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath){//確定好起始結點的下標size_t srci = GetVertexIndex(src);int n = _vertexs.size();//我們先讓所有的最短路徑無窮。即還未求出來dist.resize(n, Max_W);//注意源節點到源節點的最短路徑一定是0dist[srci] = 0;//我們讓所有的路徑都設置為-1，意味著所有的結點都沒有找出來最短路徑pPath.resize(n, -1);//這是表示起點它的路徑就是它自己，這步其實只是為了讓起點和為求出最短路徑給分開表示。不然都用-1可能會混亂pPath[srci] = srci;//這個S集合代表我們已經求出最短路徑的集合。如果是true代表著這個結點早已求出了最短路徑。false代表未求出vector<bool> S(n, false);//注意這里我們做一下特殊處理，雖然我們起點它本來就應該放在這個集合里面，但是我們還是先讓它為false。這里我們其實是想與下面的循環進行合并//所以迫不得已做的操作，因為一旦將某個結點設置為true，那么它的相鄰的結點路徑也應該被更新一下，那么這里就要把下面的對于代碼拷貝一份。//所以為了讓代碼簡潔，我們直接不寫這一步了，和下面的進行合并//S[srci] = true;//這里只是控制一下循環次數，因為我們要求所有的結點都要被遍歷一下，而每次只會遍歷一個結點，即將一個結點給放入S集合。//我們每次點亮的一定是之前從未遍歷過的結點for(int j = 0; j < n; j++){//Dijkstra算法要求每次都要找出一個，還沒有被訪問過的（不在S集合的），并且是有路徑的，且路徑是當前最小的一個結點//對于第一次找到的就是srci以及所對應的0值int u = 0;W min = Max_W;for (int i = 0; i < n; i++){if (S[i] == false && dist[i] < min){u = i;min = dist[i];}}//找到以后，我們可以讓他加入S集合，代表它已經被訪問過了。借助這里找到了srci，并且使他加入到S集合S[u] = true;//松弛更新u連接頂點v， srci->u + u->v < srci->v 就更新//注意，這里我們需要的是找到我們新加入S集合的鄰接的頂點，然后判斷是不是需要更新最短路徑，//但是我們一開始并不知道，所以我們遍歷所有的結點，依次判斷條件是否滿足for (int v = 0; v < n; v++){//我們這個要更新的不能是我們之前已經訪問過的了。因為之前訪問過的一定是最短路徑了！if (S[v] == false &&//因為是要鄰接的頂點，它必須要直接連通的兩個頂點。所以用這個條件進行排除_matrix[u][v] != Max_W//這是為了看一看用這個算出來的是不是小于我們原來的路徑，如果是，那么最短路徑就變成它了&& dist[u] + _matrix[u][v] < dist[v]){//更新最短路徑dist[v] = dist[u] + _matrix[u][v];//更新路徑的樹pPath[v] = u;}}}}

4.負權值帶來的問題

我們看一下下面的測試用例

對于下面的圖

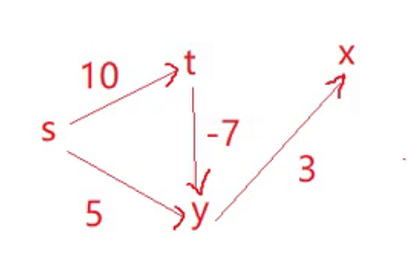
image-20240222013946282

	void TestGraphDijkstra(){const char* str = "sytx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 10);g.AddEdge('s', 'y', 5);g.AddEdge('t', 'y', -7);g.AddEdge('y', 'x', 3);vector<int> dist;vector<int> parentPath;g.Dijkstra('s', dist, parentPath);g.PrintShortPath('s', dist, parentPath);}

我們的運行結果為

image-20240222014018356

其實我們可以很容易的發現,第一條路徑和第三條路徑的最短距離,直接從圖中去看的話應該是3和6才對,但是結果居然是5和8.

它的具體步驟如下

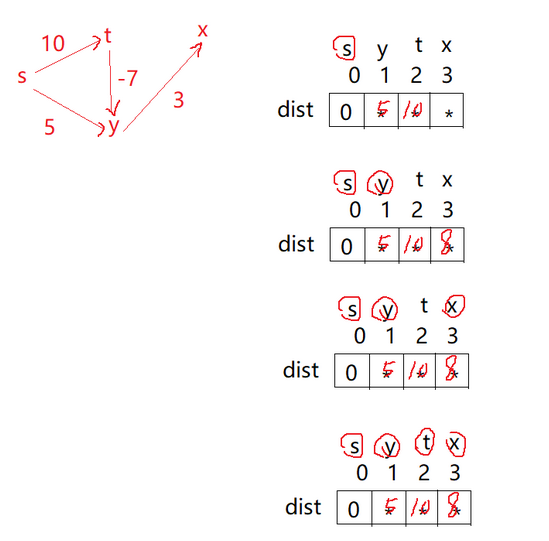
image-20240222014504325

所以它的最終是出現了問題

Dijkstra算法無法解決負權值問題主要有兩個原因：

  1. Dijkstra算法的基本思想是貪心算法，它總是選擇當前距離起始點最近（或說權重最小）的頂點進行處理。如果圖中存在負權重的邊，那么已經確定最短路徑的頂點的最短路徑可能會因為這個負權重的邊而改變，這與Dijkstra算法“確定的最短路徑就是永久不變的”初衷相矛盾。
  2. 如果圖中存在負權重的環路，Dijkstra算法可能會陷入無限循環中，因為每次經過這個負權重的環，都能使得路徑的權值變小。

因此，如果圖中邊的權值存在負值，我們通常使用Bellman-Ford算法或者Floyd-Warshall算法，這些算法能正確處理負權值的情況。

這個算法的時間復雜度是O(N2)，空間復雜度是O(N)

三、單源最短路徑 – Bellman-Ford算法

1.算法思想

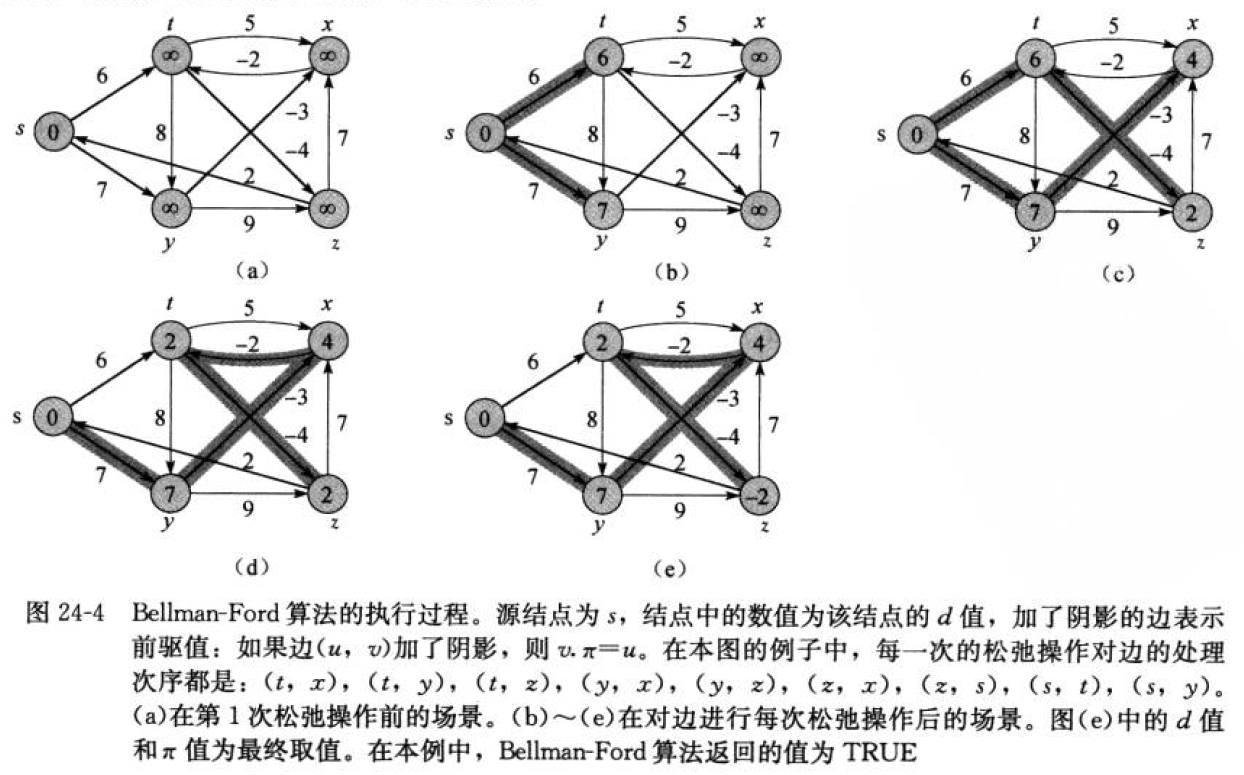
Dijkstra算法只能用來解決正權圖的單源最短路徑問題，但有些題目會出現負權圖。這時這個算法就不能幫助我們解決問題了，而bellman—ford算法可以解決負權圖的單源最短路徑問題。它的優點是可以解決有負權邊的單源最短路徑問題，而且可以用來判斷是否有負權回路。它也有明顯的缺點，它的時間復雜度 O(N*E) (N是點數，E是邊數)普遍是要高于Dijkstra算法O(N2)的。像這里如果我們使用鄰接矩陣實現，那么遍歷所有邊的數量的時間復雜度就是O(N^3)，這里也可以看出來Bellman-Ford就是一種暴力求解更新

image-20240224125506279

2.算法實現

如下代碼所示

namespace matrix
{//V代表頂點， W是weight代表權值，MAX_W代表權值的最大值，Direction代表是有向圖還是無向圖,flase表示無向template<class V, class W, W Max_W = INT_MAX, bool Direction = false>class Graph{typedef Graph<V, W, Max_W, Direction> Self;public:Graph() = default;//圖的創建//1. IO輸入 不方便測試//2. 圖結構關系寫到文件，讀取文件//3. 手動添加邊Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; i++){_vertexs.push_back(a[i]);_indexMap[a[i]] = i;}_matrix.resize(n);for (size_t i = 0; i < _matrix.size(); i++){_matrix[i].resize(n, Max_W);}}size_t GetVertexIndex(const V& v){//return _indexMap[v];auto it = _indexMap.find(v);if (it != _indexMap.end()){return it->second;}else{//assert(false)throw invalid_argument("頂點不存在");return -1;}}void _AddEdge(size_t srci, size_t dsti, const W& w){_matrix[srci][dsti] = w;if (Direction == false){_matrix[dsti][srci] = w;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVertexIndex(src);size_t dsti = GetVertexIndex(dst);_AddEdge(srci, dsti, w);}void Print(){for (size_t i = 0; i < _vertexs.size(); i++){cout << "[" << i << "]" << "->" << _vertexs[i] << endl;}cout << endl;cout << "   ";for (int i = 0; i < _vertexs.size(); i++){//cout << _vertexs[i] << " ";printf("%-3d ", i);}cout << endl;for (size_t i = 0; i < _matrix.size(); i++){//cout << _vertexs[i] << " ";printf("%d ", i);for (size_t j = 0; j < _matrix[i].size(); j++){if (_matrix[i][j] == INT_MAX){cout << " *  ";}else{printf(" %d  ", _matrix[i][j]);//cout << _matrix[i][j] << " ";}}cout << endl;}for (size_t i = 0; i < _matrix.size(); i++){for (size_t j = 0; j < _matrix[i].size(); j++){if (i < j && _matrix[i][j] != Max_W){cout << _vertexs[i] << "->" << _vertexs[j] << ":" << _matrix[i][j] << endl;}}}}void BFS(const V& src){int srci = GetVertexIndex(src);queue<int> q; //廣度遍歷的隊列vector<bool> visited(_vertexs.size(), false); //標記數組q.push(srci); //起點入隊visited[srci] = true; //已經被遍歷過了while (!q.empty()){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << endl;//把front頂點的鄰接頂點入隊列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}} void BFSLevel(const V& src){int srci = GetVertexIndex(src);queue<int> q; //廣度遍歷的隊列vector<bool> visited(_vertexs.size(), false); //標記數組q.push(srci); //起點入隊visited[srci] = true; //已經被遍歷過了int levelSize = 1;while (!q.empty()){for (int i = 0; i < levelSize; i++){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << " ";//把front頂點的鄰接頂點入隊列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}cout << endl;levelSize = q.size();}}void _DFS(size_t srci, vector<bool>& visited){cout << srci << ":" << _vertexs[srci] << endl;visited[srci] = true;for (int i = 0; i < _matrix[srci].size(); i++){if (_matrix[srci][i] != Max_W && visited[i] == false){_DFS(i, visited);}}}void DFS(const V& src){int srci = GetVertexIndex(src);vector<bool> visited(_vertexs.size(), false);_DFS(srci, visited);}struct Edge{int _srci;int _dsti;W _w;Edge(int srci, int dsti, W w):_srci(srci),_dsti(dsti),_w(w){}bool operator>(const Edge& e) const{return this->_w > e._w;}};//傳入的是一個只有結點的，沒有邊的圖W Kruskal(Self& minTree){//先將所有的邊，按照小堆的方式進行組織起來priority_queue<Edge, vector<Edge>, greater<Edge>> minque;size_t n = _vertexs.size();for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){//由于這里是無向圖，他是一個對稱矩陣，但是我們的邊只考慮一半就已經可以了。剩下的就重復了。if (i < j && _matrix[i][j] != Max_W){//已經按照自身的，帶有邊的圖，將所有的邊的信息全部組織好了minque.push(Edge(i, j, _matrix[i][j]));}}}//因為最小生成樹一定是n-1條邊，所以我們現在要選出n-1條邊，size是計數器int size = 0;//用于計算權值W totalW = W();//最關鍵的問題是判環，這里我們可以用并查集去檢測是否這兩個頂點在一個集合里面，如果在集合里面，說明一定是連通的，在加上就成環了UnionFindSet ufs(n);//開始選邊，我們要考慮到所有的邊while (!minque.empty()){//取出一個最小的邊，然后就可以將他踢出優先級隊列了，如果被選中不需要它了，如果沒有被選中，那只能是因為出現環了才不要它了。Edge min = minque.top();minque.pop();//看看是否在一個集合里面，如果在一個集合里面，那么他們已經是連通了，沒必要在連通，還想要連通那么一定是環！if (!ufs.InSet(min._srci, min._dsti)){//我們可以看看我們選出來的邊cout << _vertexs[min._srci] << "-" << _vertexs[min._dsti] << ":" << min._w << endl;//該邊是符合的，我們直接為這個圖加上邊minTree._AddEdge(min._srci, min._dsti, min._w);//加上之后，就連通了，我們讓他們形成集合ufs.Union(min._srci, min._dsti);//我們一定只有n-1條邊，我們需要計數++size;//將總的權值要加起來totalW += min._w;}//成環的情況，我們只是看看這是哪條邊else{cout << "構成環啦！:";cout << _vertexs[min._srci] << "-" << _vertexs[min._dsti] << ":" << min._w << endl;}}//上面的循環中，如果圖是連通的，那么最終一定選出來的是n-1條邊。除非圖是不連通的。if (size == n - 1){return totalW;}//圖不連通，直接返回0else{return W();}}W Prim(Self& minTree, const V& src){size_t srci = GetVertexIndex(src);int n = _vertexs.size();//使用集合的方式//set<int> X;//set<int> Y;//X.insert(srci);//for (int i = 0; i < n; i++)//{//	if (i != srci)//	{//		Y.insert(i);//	}//}//利用vector的方式,去記錄兩個集合。vector<bool> X(n, false);vector<bool> Y(n, true);X[srci] = true;Y[srci] = false;//從X->Y集合中連接的邊去選最小的邊priority_queue<Edge, vector<Edge>, greater<Edge>> minq;//把目前為止X集合（僅僅只有起點）的相關的邊，全部放入優先級隊列中for (int i = 0; i < n; i++){if (_matrix[srci][i] != Max_W){minq.push(Edge(srci, i, _matrix[srci][i]));}}//size用來判斷是否達到最小生成樹的個數n-1,totalW用來計算權值之和size_t size = 0;W totalW = W();//我們開始在優先級隊列中去尋找while (!minq.empty()){//在優先級隊列中找到一個最小的元素，由于優先級隊列中的一定是我們X集合可以延申的邊。所以是滿足Prim的選邊條件的Edge min = minq.top();//如果邊使用了，那么就不用了，如果不使用，那肯定是因為環才導致的，那也不要了minq.pop();//這里比較巧妙，因為根據我們的算法思想，我們選邊的時候一定是從X集合的某一個頂點開始的，然后去找一個不在X集合里面的頂點//所以這里我們可以直接判斷目的點是否在X集合里面，如果在，那么一定是環。如果不是，才可以把這條邊給加上去if (X[min._dsti]){//cout << "構成環：";//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;continue;}//把邊給加上去minTree._AddEdge(min._srci, min._dsti, min._w);//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;//X.insert(min._dsti);//Y.erase(min._dsti);//處理一下目的點的邊X[min._dsti] = true;Y[min._dsti] = false;++size;totalW += min._w;//這里相當于一次優化，因為該循環一定可以保證選出來的n-1條邊是最小生成樹，//后面的優先級隊列中的任何一條邊一定會導致出現環，會在前面的檢測目的點是否在X集合中被處理掉。//這里則是直接不用繼續入其他的邊進入隊列了。可以提高一些效率，減少無用的操作if (size == n - 1){break;}//當一條邊添加完成后，它就屬于X集合了，我們可以將該點所延申出的邊給加入到優先級隊列中//只有該邊存在，且目的地沒有被加入過的時候，才會入隊列。值得耐人尋味的是，這里雖然已經處理過一次可能出現環的情況了//但是可能由于在添加邊的時候，導致某些優先級隊列中的邊會導致構成環了，所以就有了前面的再次根據目的地時候在X集合中去判環for (int i = 0; i < n; i++){if (_matrix[min._dsti][i] != Max_W && X[i] == false){minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));}}}if (size == n - 1){return totalW;}else{return W();}}void PrintShortPath(const V& src, const vector<W>& dist, const vector<int>& pPath){size_t srci = GetVertexIndex(src);int n = _vertexs.size();for (int i = 0; i < n; i++){if (i != srci){cout << "[" << "pathlenth:" << dist[i] << "]";stack<int> path;size_t parent = i;while (parent != srci){path.push(parent);parent = pPath[parent];}path.push(parent);cout << "path:";while (!path.empty()){ int top = path.top();path.pop();cout << _vertexs[top] << "->";}cout << "nullptr" << endl;}}}//src是起始結點，dist數組的內容是存放最短路徑值的權值，即每個元素的內容代表著從起始結點到該結點的最短路徑//pPath數組是路徑的數組，因為有時候我們需要求出路徑的具體走法，所以我們可以用數組的方式，類似于并查集去尋找路徑的方式，建立一顆樹void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath){//確定好起始結點的下標size_t srci = GetVertexIndex(src);int n = _vertexs.size();//我們先讓所有的最短路徑無窮。即還未求出來dist.resize(n, Max_W);//注意源節點到源節點的最短路徑一定是0dist[srci] = 0;//我們讓所有的路徑都設置為-1，意味著所有的結點都沒有找出來最短路徑pPath.resize(n, -1);//這是表示起點它的路徑就是它自己，這步其實只是為了讓起點和為求出最短路徑給分開表示。不然都用-1可能會混亂pPath[srci] = srci;//這個S集合代表我們已經求出最短路徑的集合。如果是true代表著這個結點早已求出了最短路徑。false代表未求出vector<bool> S(n, false);//注意這里我們做一下特殊處理，雖然我們起點它本來就應該放在這個集合里面，但是我們還是先讓它為false。這里我們其實是想與下面的循環進行合并//所以迫不得已做的操作，因為一旦將某個結點設置為true，那么它的相鄰的結點路徑也應該被更新一下，那么這里就要把下面的對于代碼拷貝一份。//所以為了讓代碼簡潔，我們直接不寫這一步了，和下面的進行合并//S[srci] = true;//這里只是控制一下循環次數，因為我們要求所有的結點都要被遍歷一下，而每次只會遍歷一個結點，即將一個結點給放入S集合。//我們每次點亮的一定是之前從未遍歷過的結點for(int j = 0; j < n; j++){//Dijkstra算法要求每次都要找出一個，還沒有被訪問過的（不在S集合的），并且是有路徑的，且路徑是當前最小的一個結點//對于第一次找到的就是srci以及所對應的0值int u = 0;W min = Max_W;for (int i = 0; i < n; i++){if (S[i] == false && dist[i] < min){u = i;min = dist[i];}}//找到以后，我們可以讓他加入S集合，代表它已經被訪問過了。借助這里找到了srci，并且使他加入到S集合S[u] = true;//松弛更新u連接頂點v， srci->u + u->v < srci->v 就更新//注意，這里我們需要的是找到我們新加入S集合的鄰接的頂點，然后判斷是不是需要更新最短路徑，//但是我們一開始并不知道，所以我們遍歷所有的結點，依次判斷條件是否滿足for (int v = 0; v < n; v++){//我們這個要更新的不能是我們之前已經訪問過的了。因為之前訪問過的一定是最短路徑了！if (S[v] == false &&//因為是要鄰接的頂點，它必須要直接連通的兩個頂點。所以用這個條件進行排除_matrix[u][v] != Max_W//這是為了看一看用這個算出來的是不是小于我們原來的路徑，如果是，那么最短路徑就變成它了&& dist[u] + _matrix[u][v] < dist[v]){//更新最短路徑dist[v] = dist[u] + _matrix[u][v];//更新路徑的樹pPath[v] = u;}}}}bool BellmanFord(const V& src, vector<W>& dist, vector<int>& parentPath){size_t n = _vertexs.size();size_t srci = GetVertexIndex(src);dist.resize(n, Max_W);dist[srci] = W();parentPath.resize(n, -1);parentPath[srci] = srci;for (int k = 0; k < n; k++){bool update = false;for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){update = true;//srci->i + i->j => srci->jif (_matrix[i][j] != Max_W && dist[i] + _matrix[i][j] < dist[j]){dist[j] = dist[i] + _matrix[i][j];parentPath[j] = i;}}}if (update == false){break;}}//還能更新就是帶有負權回路for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){//srci->i + i->j => srci->jif (_matrix[i][j] != Max_W && dist[i] + _matrix[i][j] < dist[j]){return false;}}}}private:vector<V> _vertexs; //頂點集合map<V, int> _indexMap; //頂點對應的下標關系vector<vector<W>> _matrix; //臨界矩陣};void TestGraphBellmanFord(){const char* str = "syztx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 6);g.AddEdge('s', 'y', 7);g.AddEdge('y', 'z', 9);g.AddEdge('y', 'x', -3);g.AddEdge('z', 's', 2);g.AddEdge('z', 'x', 7);g.AddEdge('t', 'x', 5);g.AddEdge('t', 'y', 8);g.AddEdge('t', 'z', -4);g.AddEdge('x', 't', -2);vector<int> dist;vector<int> parentPath;if (g.BellmanFord('s', dist, parentPath)){g.PrintShortPath('s', dist, parentPath);}else{cout << "存在負權回路" << endl;}}void TestGraphDijkstra(){//const char* str = "syztx";//Graph<char, int, INT_MAX, true> g(str, strlen(str));//g.AddEdge('s', 't', 10);//g.AddEdge('s', 'y', 5);//g.AddEdge('y', 't', 3);//g.AddEdge('y', 'x', 9);//g.AddEdge('y', 'z', 2);//g.AddEdge('z', 's', 7);//g.AddEdge('z', 'x', 6);//g.AddEdge('t', 'y', 2);//g.AddEdge('t', 'x', 1);//g.AddEdge('x', 'z', 4);//vector<int> dist;//vector<int> parentPath;//g.Dijkstra('s', dist, parentPath);//g.PrintShortPath('s', dist, parentPath);const char* str = "sytx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 10);g.AddEdge('s', 'y', 5);g.AddEdge('t', 'y', -7);g.AddEdge('y', 'x', 3);vector<int> dist;vector<int> parentPath;g.Dijkstra('s', dist, parentPath);g.PrintShortPath('s', dist, parentPath);}void TestGraph(){Graph<char, int, INT_MAX, true> g("0123", 4);g.AddEdge('0', '1', 1);g.AddEdge('0', '3', 4);g.AddEdge('1', '3', 2);g.AddEdge('1', '2', 9);g.AddEdge('2', '3', 8);g.AddEdge('2', '1', 5);g.AddEdge('2', '0', 3);g.AddEdge('3', '2', 6);g.Print();}void TestGraphBDFS(){string a[] = { "張三", "李四", "王五", "趙六", "周七" };Graph<string, int> g1(a, sizeof(a) / sizeof(string));g1.AddEdge("張三", "李四", 100);g1.AddEdge("張三", "王五", 200);g1.AddEdge("王五", "趙六", 30);g1.AddEdge("王五", "周七", 30);g1.Print();g1.BFS("張三");cout << endl;g1.BFSLevel("張三");cout << endl;g1.DFS("張三");}void TestGraphMinTree(){const char* str = "abcdefghi";Graph<char, int> g(str, strlen(str));g.AddEdge('a', 'b', 4);g.AddEdge('a', 'h', 8);//g.AddEdge('a', 'h', 9);g.AddEdge('b', 'c', 8);g.AddEdge('b', 'h', 11); g.AddEdge('c', 'i', 2);g.AddEdge('c', 'f', 4);g.AddEdge('c', 'd', 7);g.AddEdge('d', 'f', 14);g.AddEdge('d', 'e', 9);g.AddEdge('e', 'f', 10);g.AddEdge('f', 'g', 2);g.AddEdge('g', 'h', 1);g.AddEdge('g', 'i', 6);g.AddEdge('h', 'i', 7);//Graph<char, int> kminTree;//Graph<char, int> kminTree(str, strlen(str));//cout << "Kruskal:" << g.Kruskal(kminTree) << endl;//kminTree.Print();//Graph<char, int> pminTree(str, strlen(str));//cout << "Prim:" << g.Prim(pminTree, 'a') << endl;//pminTree.Print();for (int i = 0; i < strlen(str); i++){Graph<char, int> pminTree(str, strlen(str));cout << "Prim:" << str[i] << ":" << g.Prim(pminTree, str[i]) << endl;}}
}

Bellman-Ford算法的基本思路是：

  • 首先是遍歷所有的邊。只要srci->i + i->j的距離小于之前的srci->j的距離。那么就進行更新，同時更新父路徑
  • 不過這里可能存在的一個問題是權值和路徑對不上的問題，因為只要更新出了更短的一條路徑，可能就會影響其他路徑。不過我們會發現如果在更新一次的話，那么就會修正這個問題，但是更新路徑又會影響其他路徑。所以還需要繼續更新，最多會更新n輪。最多也就是每個結點都更新一次。
  • 一旦我們發現某一輪沒有更新，那么后序的也絕不可能被影響到，所以后面可以不用更新了。

運行結果為

image-20240224143254165

3.SPFA優化

上面代碼的時間復雜度是O(N3),我們可以使用SPFA優化

SPFA優化的基本思想是

  • 第一輪更新，所有邊入隊列
  • 后面的輪次，更新最短路徑的邊入隊列
  • 每次只對隊列里面的邊進行操作

4.負權回路

如下測試用例所示

	void TestGraphBellmanFord(){//微調圖結構，帶有負權回路的測試const char* str = "syztx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 6);g.AddEdge('s', 'y', 7);g.AddEdge('y', 'x', -3);g.AddEdge('y', 'z', 9);g.AddEdge('y', 'x', -3);g.AddEdge('y', 's', 1); // 新增g.AddEdge('z', 's', 2);g.AddEdge('z', 'x', 7);g.AddEdge('t', 'x', 5);g.AddEdge('t', 'y', -8); // 更改g.AddEdge('t', 'z', -4);g.AddEdge('x', 't', -2);vector<int> dist;vector<int> parentPath;if (g.BellmanFord('s', dist, parentPath)){g.PrintShortPath('s', dist, parentPath);}else{cout << "存在負權回路" << endl;}}

在這個圖中存在負權回路

我們用上面的Bellman-Ford算法可以去檢測負權回路，因為最多更新n輪，如果還繼續更新，那么只能是負權回路惹的禍。所以可以借此來檢測負權回路

運行結果為

image-20240224143600279

注意：

負權回路，神仙難救，求不出最短路徑

四、多源最短路徑 – Floyd-Warshall算法

1.算法思想

Floyd-Warshall算法是解決任意兩點間的最短路徑的一種算法。
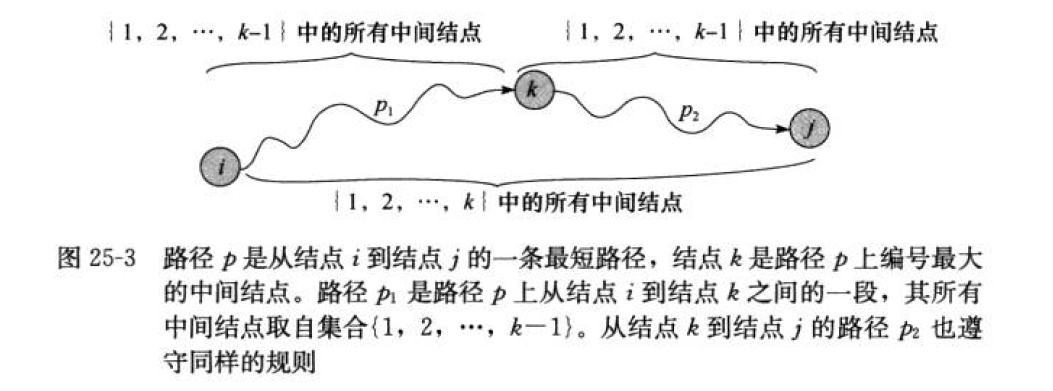
Floyd算法考慮的是一條最短路徑的中間節點，即簡單路徑p={v1,v2,…,vn}上除v1和vn的任意節點。
設k是p的一個中間節點，那么從i到j的最短路徑p就被分成i到k和k到j的兩段最短路徑p1，p2。p1是從i到k且中間節點屬于{1,2，…,k-1}取得的一條最短路徑。p2是從k到j且中間節點屬于{1，2，…，k-1}取得的一條最短路徑。

image-20240224161137658

image-20240224161210688

2.算法實現

namespace matrix
{//V代表頂點， W是weight代表權值，MAX_W代表權值的最大值，Direction代表是有向圖還是無向圖,flase表示無向template<class V, class W, W Max_W = INT_MAX, bool Direction = false>class Graph{typedef Graph<V, W, Max_W, Direction> Self;public:Graph() = default;//圖的創建//1. IO輸入 不方便測試//2. 圖結構關系寫到文件，讀取文件//3. 手動添加邊Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; i++){_vertexs.push_back(a[i]);_indexMap[a[i]] = i;}_matrix.resize(n);for (size_t i = 0; i < _matrix.size(); i++){_matrix[i].resize(n, Max_W);}}size_t GetVertexIndex(const V& v){//return _indexMap[v];auto it = _indexMap.find(v);if (it != _indexMap.end()){return it->second;}else{//assert(false)throw invalid_argument("頂點不存在");return -1;}}void _AddEdge(size_t srci, size_t dsti, const W& w){_matrix[srci][dsti] = w;if (Direction == false){_matrix[dsti][srci] = w;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVertexIndex(src);size_t dsti = GetVertexIndex(dst);_AddEdge(srci, dsti, w);}void Print(){for (size_t i = 0; i < _vertexs.size(); i++){cout << "[" << i << "]" << "->" << _vertexs[i] << endl;}cout << endl;cout << "   ";for (int i = 0; i < _vertexs.size(); i++){//cout << _vertexs[i] << " ";printf("%-3d ", i);}cout << endl;for (size_t i = 0; i < _matrix.size(); i++){//cout << _vertexs[i] << " ";printf("%d ", i);for (size_t j = 0; j < _matrix[i].size(); j++){if (_matrix[i][j] == INT_MAX){cout << " *  ";}else{printf(" %d  ", _matrix[i][j]);//cout << _matrix[i][j] << " ";}}cout << endl;}for (size_t i = 0; i < _matrix.size(); i++){for (size_t j = 0; j < _matrix[i].size(); j++){if (i < j && _matrix[i][j] != Max_W){cout << _vertexs[i] << "->" << _vertexs[j] << ":" << _matrix[i][j] << endl;}}}}void BFS(const V& src){int srci = GetVertexIndex(src);queue<int> q; //廣度遍歷的隊列vector<bool> visited(_vertexs.size(), false); //標記數組q.push(srci); //起點入隊visited[srci] = true; //已經被遍歷過了while (!q.empty()){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << endl;//把front頂點的鄰接頂點入隊列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}} void BFSLevel(const V& src){int srci = GetVertexIndex(src);queue<int> q; //廣度遍歷的隊列vector<bool> visited(_vertexs.size(), false); //標記數組q.push(srci); //起點入隊visited[srci] = true; //已經被遍歷過了int levelSize = 1;while (!q.empty()){for (int i = 0; i < levelSize; i++){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << " ";//把front頂點的鄰接頂點入隊列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}cout << endl;levelSize = q.size();}}void _DFS(size_t srci, vector<bool>& visited){cout << srci << ":" << _vertexs[srci] << endl;visited[srci] = true;for (int i = 0; i < _matrix[srci].size(); i++){if (_matrix[srci][i] != Max_W && visited[i] == false){_DFS(i, visited);}}}void DFS(const V& src){int srci = GetVertexIndex(src);vector<bool> visited(_vertexs.size(), false);_DFS(srci, visited);}struct Edge{int _srci;int _dsti;W _w;Edge(int srci, int dsti, W w):_srci(srci),_dsti(dsti),_w(w){}bool operator>(const Edge& e) const{return this->_w > e._w;}};//傳入的是一個只有結點的，沒有邊的圖W Kruskal(Self& minTree){//先將所有的邊，按照小堆的方式進行組織起來priority_queue<Edge, vector<Edge>, greater<Edge>> minque;size_t n = _vertexs.size();for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){//由于這里是無向圖，他是一個對稱矩陣，但是我們的邊只考慮一半就已經可以了。剩下的就重復了。if (i < j && _matrix[i][j] != Max_W){//已經按照自身的，帶有邊的圖，將所有的邊的信息全部組織好了minque.push(Edge(i, j, _matrix[i][j]));}}}//因為最小生成樹一定是n-1條邊，所以我們現在要選出n-1條邊，size是計數器int size = 0;//用于計算權值W totalW = W();//最關鍵的問題是判環，這里我們可以用并查集去檢測是否這兩個頂點在一個集合里面，如果在集合里面，說明一定是連通的，在加上就成環了UnionFindSet ufs(n);//開始選邊，我們要考慮到所有的邊while (!minque.empty()){//取出一個最小的邊，然后就可以將他踢出優先級隊列了，如果被選中不需要它了，如果沒有被選中，那只能是因為出現環了才不要它了。Edge min = minque.top();minque.pop();//看看是否在一個集合里面，如果在一個集合里面，那么他們已經是連通了，沒必要在連通，還想要連通那么一定是環！if (!ufs.InSet(min._srci, min._dsti)){//我們可以看看我們選出來的邊cout << _vertexs[min._srci] << "-" << _vertexs[min._dsti] << ":" << min._w << endl;//該邊是符合的，我們直接為這個圖加上邊minTree._AddEdge(min._srci, min._dsti, min._w);//加上之后，就連通了，我們讓他們形成集合ufs.Union(min._srci, min._dsti);//我們一定只有n-1條邊，我們需要計數++size;//將總的權值要加起來totalW += min._w;}//成環的情況，我們只是看看這是哪條邊else{cout << "構成環啦！:";cout << _vertexs[min._srci] << "-" << _vertexs[min._dsti] << ":" << min._w << endl;}}//上面的循環中，如果圖是連通的，那么最終一定選出來的是n-1條邊。除非圖是不連通的。if (size == n - 1){return totalW;}//圖不連通，直接返回0else{return W();}}W Prim(Self& minTree, const V& src){size_t srci = GetVertexIndex(src);int n = _vertexs.size();//使用集合的方式//set<int> X;//set<int> Y;//X.insert(srci);//for (int i = 0; i < n; i++)//{//	if (i != srci)//	{//		Y.insert(i);//	}//}//利用vector的方式,去記錄兩個集合。vector<bool> X(n, false);vector<bool> Y(n, true);X[srci] = true;Y[srci] = false;//從X->Y集合中連接的邊去選最小的邊priority_queue<Edge, vector<Edge>, greater<Edge>> minq;//把目前為止X集合（僅僅只有起點）的相關的邊，全部放入優先級隊列中for (int i = 0; i < n; i++){if (_matrix[srci][i] != Max_W){minq.push(Edge(srci, i, _matrix[srci][i]));}}//size用來判斷是否達到最小生成樹的個數n-1,totalW用來計算權值之和size_t size = 0;W totalW = W();//我們開始在優先級隊列中去尋找while (!minq.empty()){//在優先級隊列中找到一個最小的元素，由于優先級隊列中的一定是我們X集合可以延申的邊。所以是滿足Prim的選邊條件的Edge min = minq.top();//如果邊使用了，那么就不用了，如果不使用，那肯定是因為環才導致的，那也不要了minq.pop();//這里比較巧妙，因為根據我們的算法思想，我們選邊的時候一定是從X集合的某一個頂點開始的，然后去找一個不在X集合里面的頂點//所以這里我們可以直接判斷目的點是否在X集合里面，如果在，那么一定是環。如果不是，才可以把這條邊給加上去if (X[min._dsti]){//cout << "構成環：";//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;continue;}//把邊給加上去minTree._AddEdge(min._srci, min._dsti, min._w);//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;//X.insert(min._dsti);//Y.erase(min._dsti);//處理一下目的點的邊X[min._dsti] = true;Y[min._dsti] = false;++size;totalW += min._w;//這里相當于一次優化，因為該循環一定可以保證選出來的n-1條邊是最小生成樹，//后面的優先級隊列中的任何一條邊一定會導致出現環，會在前面的檢測目的點是否在X集合中被處理掉。//這里則是直接不用繼續入其他的邊進入隊列了。可以提高一些效率，減少無用的操作if (size == n - 1){break;}//當一條邊添加完成后，它就屬于X集合了，我們可以將該點所延申出的邊給加入到優先級隊列中//只有該邊存在，且目的地沒有被加入過的時候，才會入隊列。值得耐人尋味的是，這里雖然已經處理過一次可能出現環的情況了//但是可能由于在添加邊的時候，導致某些優先級隊列中的邊會導致構成環了，所以就有了前面的再次根據目的地時候在X集合中去判環for (int i = 0; i < n; i++){if (_matrix[min._dsti][i] != Max_W && X[i] == false){minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));}}}if (size == n - 1){return totalW;}else{return W();}}void PrintShortPath(const V& src, const vector<W>& dist, const vector<int>& pPath){size_t srci = GetVertexIndex(src);int n = _vertexs.size();for (int i = 0; i < n; i++){if (i != srci){cout << "[" << "pathlenth:" << dist[i] << "]";stack<int> path;size_t parent = i;while (parent != srci){path.push(parent);parent = pPath[parent];}path.push(parent);cout << "path:";while (!path.empty()){ int top = path.top();path.pop();cout << _vertexs[top] << "->";}cout << "nullptr" << endl;}}}//src是起始結點，dist數組的內容是存放最短路徑值的權值，即每個元素的內容代表著從起始結點到該結點的最短路徑//pPath數組是路徑的數組，因為有時候我們需要求出路徑的具體走法，所以我們可以用數組的方式，類似于并查集去尋找路徑的方式，建立一顆樹void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath){//確定好起始結點的下標size_t srci = GetVertexIndex(src);int n = _vertexs.size();//我們先讓所有的最短路徑無窮。即還未求出來dist.resize(n, Max_W);//注意源節點到源節點的最短路徑一定是0dist[srci] = 0;//我們讓所有的路徑都設置為-1，意味著所有的結點都沒有找出來最短路徑pPath.resize(n, -1);//這是表示起點它的路徑就是它自己，這步其實只是為了讓起點和為求出最短路徑給分開表示。不然都用-1可能會混亂pPath[srci] = srci;//這個S集合代表我們已經求出最短路徑的集合。如果是true代表著這個結點早已求出了最短路徑。false代表未求出vector<bool> S(n, false);//注意這里我們做一下特殊處理，雖然我們起點它本來就應該放在這個集合里面，但是我們還是先讓它為false。這里我們其實是想與下面的循環進行合并//所以迫不得已做的操作，因為一旦將某個結點設置為true，那么它的相鄰的結點路徑也應該被更新一下，那么這里就要把下面的對于代碼拷貝一份。//所以為了讓代碼簡潔，我們直接不寫這一步了，和下面的進行合并//S[srci] = true;//這里只是控制一下循環次數，因為我們要求所有的結點都要被遍歷一下，而每次只會遍歷一個結點，即將一個結點給放入S集合。//我們每次點亮的一定是之前從未遍歷過的結點for(int j = 0; j < n; j++){//Dijkstra算法要求每次都要找出一個，還沒有被訪問過的（不在S集合的），并且是有路徑的，且路徑是當前最小的一個結點//對于第一次找到的就是srci以及所對應的0值int u = 0;W min = Max_W;for (int i = 0; i < n; i++){if (S[i] == false && dist[i] < min){u = i;min = dist[i];}}//找到以后，我們可以讓他加入S集合，代表它已經被訪問過了。借助這里找到了srci，并且使他加入到S集合S[u] = true;//松弛更新u連接頂點v， srci->u + u->v < srci->v 就更新//注意，這里我們需要的是找到我們新加入S集合的鄰接的頂點，然后判斷是不是需要更新最短路徑，//但是我們一開始并不知道，所以我們遍歷所有的結點，依次判斷條件是否滿足for (int v = 0; v < n; v++){//我們這個要更新的不能是我們之前已經訪問過的了。因為之前訪問過的一定是最短路徑了！if (S[v] == false &&//因為是要鄰接的頂點，它必須要直接連通的兩個頂點。所以用這個條件進行排除_matrix[u][v] != Max_W//這是為了看一看用這個算出來的是不是小于我們原來的路徑，如果是，那么最短路徑就變成它了&& dist[u] + _matrix[u][v] < dist[v]){//更新最短路徑dist[v] = dist[u] + _matrix[u][v];//更新路徑的樹pPath[v] = u;}}}}bool BellmanFord(const V& src, vector<W>& dist, vector<int>& parentPath){size_t n = _vertexs.size();size_t srci = GetVertexIndex(src);dist.resize(n, Max_W);dist[srci] = W();parentPath.resize(n, -1);parentPath[srci] = srci;for (int k = 0; k < n; k++){bool update = false;for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){update = true;//srci->i + i->j => srci->jif (_matrix[i][j] != Max_W && dist[i] + _matrix[i][j] < dist[j]){dist[j] = dist[i] + _matrix[i][j];parentPath[j] = i;}}}if (update == false){break;}}//還能更新就是帶有負權回路for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){//srci->i + i->j => srci->jif (_matrix[i][j] != Max_W && dist[i] + _matrix[i][j] < dist[j]){return false;}}}}//vvDist中，vvDist[i][j]代表著以i為起點，到j的最短路徑//vvpPath中，vvpPath[i][j]代表著以i為起點，j為終點的最短路徑的上一個父路徑。void FloydWarShall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath){size_t n = _vertexs.size();vvDist.resize(n, vector<W>(n, Max_W));vvpPath.resize(n, vector<int>(n, -1));//把直接相連的邊更新一下for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (_matrix[i][j] != Max_W){vvDist[i][j] = _matrix[i][j];//i和j直接相連，即i->j，那么j的上一個父路徑一定是ivvpPath[i][j] = i;}if (i == j){vvDist[i][j] = W();}}}//最短路徑的更新，k要考慮每一個結點作為中間結點for (int k = 0; k < n; k++){for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){//k作為中間結點去嘗試更新所有的i->j路徑if (vvDist[i][k] != Max_W && vvDist[k][j] != Max_W&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j]){vvDist[i][j] = vvDist[i][k] + vvDist[k][j];// 從i到j的父路徑// 也就是說如果K和j直接相連，那么它的父路徑就是k本身，而此時vvPath[k][j]正好就是k本身// 如果k和j不直接相連，即 i->...->k->...->x->j,此時父路徑就是x,而此時vvpPath[k][j]的值其實也是xvvpPath[i][j] = vvpPath[k][j];}}}//打印一下權值和路徑矩陣for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (vvDist[i][j] == Max_W){printf("%3c", '*');}else{printf("%3d", vvDist[i][j]);}}cout << endl;}cout << endl;for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){printf("%3d", vvpPath[i][j]);}cout << endl;}cout << "=================" << endl;}} private:vector<V> _vertexs; //頂點集合map<V, int> _indexMap; //頂點對應的下標關系vector<vector<W>> _matrix; //臨界矩陣};void TestFloydWarShall(){const char* str = "12345";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('1', '2', 3);g.AddEdge('1', '3', 8);g.AddEdge('1', '5', -4);g.AddEdge('2', '4', 1);g.AddEdge('2', '5', 7);g.AddEdge('3', '2', 4);g.AddEdge('4', '1', 2);g.AddEdge('4', '3', -5);g.AddEdge('5', '4', 6);vector<vector<int>> vvDist;vector<vector<int>> vvParentPath;g.FloydWarShall(vvDist, vvParentPath);// 打印任意兩點之間的最短路徑for (size_t i = 0; i < strlen(str); ++i){g.PrintShortPath(str[i], vvDist[i], vvParentPath[i]);cout << endl;}}void TestGraphBellmanFord(){//const char* str = "syztx";//Graph<char, int, INT_MAX, true> g(str, strlen(str));//g.AddEdge('s', 't', 6);//g.AddEdge('s', 'y', 7);//g.AddEdge('y', 'z', 9);//g.AddEdge('y', 'x', -3);//g.AddEdge('z', 's', 2);//g.AddEdge('z', 'x', 7);//g.AddEdge('t', 'x', 5);//g.AddEdge('t', 'y', 8);//g.AddEdge('t', 'z', -4);//g.AddEdge('x', 't', -2);//vector<int> dist;//vector<int> parentPath;//if (g.BellmanFord('s', dist, parentPath))//{//	g.PrintShortPath('s', dist, parentPath);//}//else//{//	cout << "存在負權回路" << endl;//}//微調圖結構，帶有負權回路的測試const char* str = "syztx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 6);g.AddEdge('s', 'y', 7);g.AddEdge('y', 'x', -3);g.AddEdge('y', 'z', 9);g.AddEdge('y', 'x', -3);g.AddEdge('y', 's', 1); // 新增g.AddEdge('z', 's', 2);g.AddEdge('z', 'x', 7);g.AddEdge('t', 'x', 5);g.AddEdge('t', 'y', -8); // 更改g.AddEdge('t', 'z', -4);g.AddEdge('x', 't', -2);vector<int> dist;vector<int> parentPath;if (g.BellmanFord('s', dist, parentPath)){g.PrintShortPath('s', dist, parentPath);}else{cout << "存在負權回路" << endl;}}void TestGraphDijkstra(){//const char* str = "syztx";//Graph<char, int, INT_MAX, true> g(str, strlen(str));//g.AddEdge('s', 't', 10);//g.AddEdge('s', 'y', 5);//g.AddEdge('y', 't', 3);//g.AddEdge('y', 'x', 9);//g.AddEdge('y', 'z', 2);//g.AddEdge('z', 's', 7);//g.AddEdge('z', 'x', 6);//g.AddEdge('t', 'y', 2);//g.AddEdge('t', 'x', 1);//g.AddEdge('x', 'z', 4);//vector<int> dist;//vector<int> parentPath;//g.Dijkstra('s', dist, parentPath);//g.PrintShortPath('s', dist, parentPath);const char* str = "sytx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 10);g.AddEdge('s', 'y', 5);g.AddEdge('t', 'y', -7);g.AddEdge('y', 'x', 3);vector<int> dist;vector<int> parentPath;g.Dijkstra('s', dist, parentPath);g.PrintShortPath('s', dist, parentPath);}void TestGraph(){Graph<char, int, INT_MAX, true> g("0123", 4);g.AddEdge('0', '1', 1);g.AddEdge('0', '3', 4);g.AddEdge('1', '3', 2);g.AddEdge('1', '2', 9);g.AddEdge('2', '3', 8);g.AddEdge('2', '1', 5);g.AddEdge('2', '0', 3);g.AddEdge('3', '2', 6);g.Print();}void TestGraphBDFS(){string a[] = { "張三", "李四", "王五", "趙六", "周七" };Graph<string, int> g1(a, sizeof(a) / sizeof(string));g1.AddEdge("張三", "李四", 100);g1.AddEdge("張三", "王五", 200);g1.AddEdge("王五", "趙六", 30);g1.AddEdge("王五", "周七", 30);g1.Print();g1.BFS("張三");cout << endl;g1.BFSLevel("張三");cout << endl;g1.DFS("張三");}void TestGraphMinTree(){const char* str = "abcdefghi";Graph<char, int> g(str, strlen(str));g.AddEdge('a', 'b', 4);g.AddEdge('a', 'h', 8);//g.AddEdge('a', 'h', 9);g.AddEdge('b', 'c', 8);g.AddEdge('b', 'h', 11); g.AddEdge('c', 'i', 2);g.AddEdge('c', 'f', 4);g.AddEdge('c', 'd', 7);g.AddEdge('d', 'f', 14);g.AddEdge('d', 'e', 9);g.AddEdge('e', 'f', 10);g.AddEdge('f', 'g', 2);g.AddEdge('g', 'h', 1);g.AddEdge('g', 'i', 6);g.AddEdge('h', 'i', 7);//Graph<char, int> kminTree;//Graph<char, int> kminTree(str, strlen(str));//cout << "Kruskal:" << g.Kruskal(kminTree) << endl;//kminTree.Print();//Graph<char, int> pminTree(str, strlen(str));//cout << "Prim:" << g.Prim(pminTree, 'a') << endl;//pminTree.Print();for (int i = 0; i < strlen(str); i++){Graph<char, int> pminTree(str, strlen(str));cout << "Prim:" << str[i] << ":" << g.Prim(pminTree, str[i]) << endl;}}
}

運行結果為

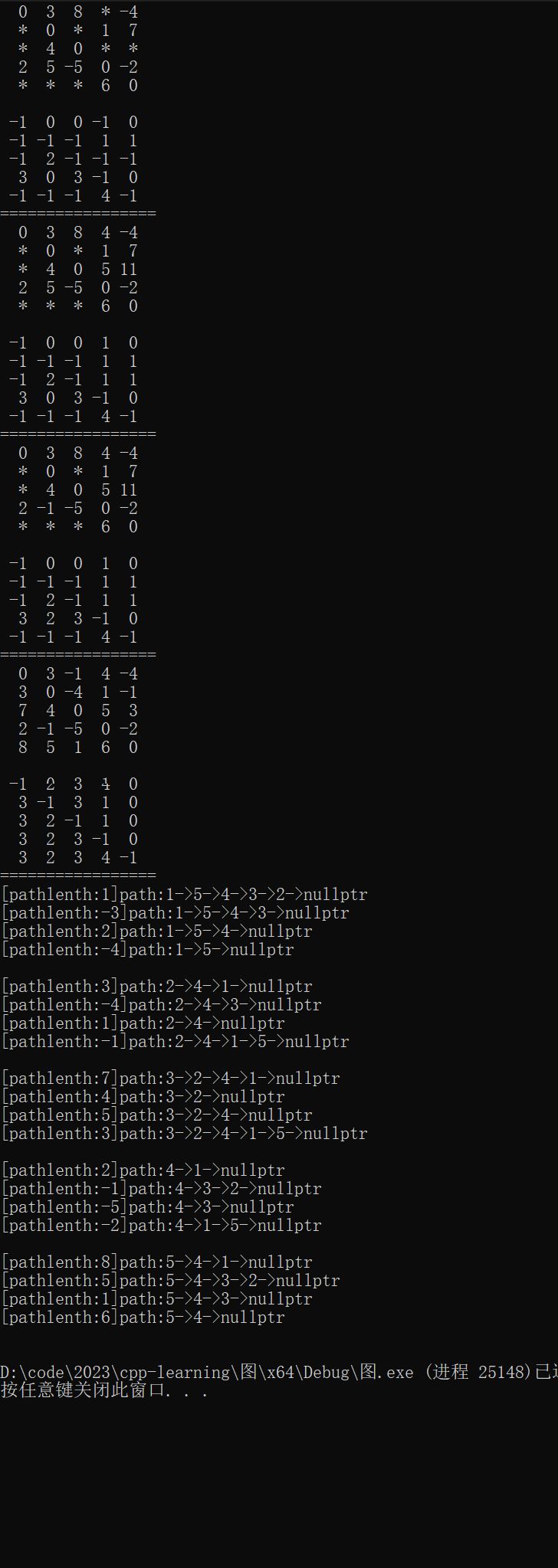
image-20240224161523162

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/714063.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/714063.shtml
英文地址，請注明出處：http://en.pswp.cn/news/714063.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

antd vue 日期控件的使用（選年份）

antd vue 日期控件的使用（選年份）

Ant Design Vue-------DatePicker 今天就講講Ant Design Vue下的控件----DatePicker 日期選擇框 結合項目中的需求&#xff0c;先講一下選擇年份如何使用&#xff0c;需求&#xff1a; &#xff08;1&#xff09;將庫中存的年份讀出到DatePicker控件里面&#xff1b; &…
閱讀更多...
Windows 10上安裝Docker

Windows 10上安裝Docker

在Windows 10上安裝Docker需要使用Docker Desktop for Windows&#xff0c;這是一個完全包含Docker工具和Docker Engine的應用程序&#xff0c;讓你可以在Windows環境中運行容器化應用程序。以下是安裝Docker Desktop for Windows的步驟&#xff1a; 系統要求檢查&#xff1a; …
閱讀更多...
推薦收藏！字節AI Lab-NLP算法（含大模型）面經總結！

推薦收藏！字節AI Lab-NLP算法（含大模型）面經總結！

節前&#xff0c;我們組織了一場算法崗技術&面試討論會&#xff0c;邀請了一些互聯網大廠同學、參加社招和校招面試的同學&#xff0c;針對大模型技術趨勢、大模型落地項目經驗分享、新手如何入門算法崗、該如何備戰、面試常考點分享等熱門話題進行了深入的討論。 今天整理…
閱讀更多...
Python調用ChatGPT API使用國內中轉key 修改接口教程

Python調用ChatGPT API使用國內中轉key 修改接口教程

大家好&#xff0c;我是淘小白~ 有的客戶使用4.0的apikey ,直接使用官方直連的apikey消費很高&#xff0c;有一位客戶一個月要消費2萬&#xff0c;想使用4.0中轉的apikey&#xff0c;使用中轉的apikey 需要修改官方的openai庫&#xff0c;下面具體說下。 1、首先確保安裝的op…
閱讀更多...
Java ElasticSearch-Linux面試題

Java ElasticSearch-Linux面試題

Java ElasticSearch-Linux面試題 前言1、守護線程的作用&#xff1f;2、鏈路追蹤Skywalking用過嗎&#xff1f;3、你對G1收集器了解嗎&#xff1f;4、你們項目用的什么垃圾收集器&#xff1f;5、內存溢出和內存泄露的區別&#xff1f;6、什么是Spring Cloud Bus&#xff1f;7、…
閱讀更多...
安裝ProxySQL，教程及安裝鏈接(網盤自提)

安裝ProxySQL，教程及安裝鏈接(網盤自提)

一、網盤下載&#xff0c;本地直傳 我網盤分享的是proxysql-2.5.5-1-centos8.x86_64.rpm&#xff0c;yum或者dnf直接安裝就行 提取碼&#xff1a;rhelhttps://pan.baidu.com/s/1nmx8-h8JEhrxQE3jsB7YQw 官方安裝地址 官網下載地址https://repo.proxysql.com/ProxySQL/ 二、…
閱讀更多...
題解：CF1889C1-Doremy‘s Drying Plan (Easy Version)

題解：CF1889C1-Doremy‘s Drying Plan (Easy Version)

題解&#xff1a;CF1889C1-Doremy’s Drying Plan (Easy Version) 一、 題意描述 1. 題目鏈接 &#xff08;1&#xff09; CF鏈接 CodeForces &#xff08;2&#xff09; 洛谷鏈接 洛谷 2. 題目翻譯 有一個長度為 n n n 的序列&#xff0c;上面有 n n n 個點&#xf…
閱讀更多...
快速搭建項目運行環境（JDK+Maven+Git+Docker+Mysql+Redis+Node.js+Nginx）+前后端項目分別部署

快速搭建項目運行環境（JDK+Maven+Git+Docker+Mysql+Redis+Node.js+Nginx）+前后端項目分別部署

JDK ①、從oracle官方網站上下載1.8版本中的最新版的JDK https://www.oracle.com/java/technologies/javase/javase-jdk8-downloads.html ②、把文件通過WinSCP或者XFTP上傳到服務器上 ③、解壓和配置環境變量 #進入安裝包目錄&#xff0c;解壓 cd /data/tmp tar -zxvf jdk-8…
閱讀更多...
【AIGC】“光影交織的戀曲：絕美情侶在藍天下的深情互動“

【AIGC】“光影交織的戀曲：絕美情侶在藍天下的深情互動“

外貌特征 (Physical Appearance)&#xff1a;給遠景鏡頭&#xff0c;這對情侶擁有出眾的容貌和氣質。男子身材挺拔&#xff0c;五官立體鮮明&#xff0c;陽光灑在他俊朗的臉龐上&#xff0c;更顯英氣逼人&#xff1b;女子則擁有一頭柔順亮麗的秀發&#xff0c;明亮的眼睛如同星…
閱讀更多...
代碼隨想錄| 深搜、797.所有可能的路徑

代碼隨想錄| 深搜、797.所有可能的路徑

回溯算法其實就是深搜&#xff0c;只不過這里的深搜是側重于在圖上搜索&#xff0c;回溯大多是在樹上搜索。 797.所有可能的路徑 完成 代碼 模板題 class Solution {List<List<Integer>> res new ArrayList<>();List<Integer> path new ArrayList…
閱讀更多...
GPT-4論文精讀【論文精讀·53】

GPT-4論文精讀【論文精讀·53】

Toolformer 今天我們來聊一下 GPT 4&#xff0c;但其實在最開始準備這期視頻的時候&#xff0c;我是準備講 Toolformer 這篇論文的&#xff0c;它是 Meta AI 在2月初的時候放出來的一篇論文。說這個大的語言模型可以利用工具了&#xff0c;比如說它就可以去調用各種各樣的API&a…
閱讀更多...
騰訊云優惠券領取的三個渠道，一個比一個優惠！

騰訊云優惠券領取的三個渠道，一個比一個優惠！

騰訊云代金券領取渠道有哪些&#xff1f;騰訊云官網可以領取、官方媒體賬號可以領取代金券、完成任務可以領取代金券&#xff0c;大家也可以在騰訊云百科蹲守代金券&#xff0c;因為騰訊云代金券領取渠道比較分散&#xff0c;騰訊云百科txybk.com專注匯總優惠代金券領取頁面&am…
閱讀更多...
Unity（第二十四部）UI

Unity（第二十四部）UI

在游戲開發中&#xff0c;用戶界面&#xff08;UI&#xff09;是至關重要的一部分。它負責與玩家進行交互&#xff0c;提供信息&#xff0c;并增強游戲的整體體驗。Unity 提供了強大的工具和功能來創建和管理 UI。 ui的底層就是畫布&#xff0c;創建畫布的時候會同時創建一個事…
閱讀更多...
19.2 基于SpringBoot電商項目:一刷(????)

19.2 基于SpringBoot電商項目:一刷(????)

19.2 基于SpringBoot電商項目一刷 1. 項目介紹2. 準備階段2.1 idea插件2.2 log4j2日志整合1. 排除springweb依賴的Logback依賴2. 引入log4j2依賴3. log4j2.xml文件3. 用戶模塊3.1 統一響應對象1. 統一響應對象2. 異常信息枚舉類3. 簡單案例3.2 業務異常處理1. 自定義業務異常類…
閱讀更多...
python筆記_位運算

python筆記_位運算

A&#xff0c;原碼反碼補碼 1&#xff0c;二進制 二進制的最高位是符號位&#xff0c;0為正&#xff0c;1為負 例 3 > 0000 0011 -3 > 1000 0011 2&#xff0c;正數 正數的原碼&#xff0c;反碼&#xff0c;補碼都一樣&#xff08;三碼合一&#xff09; 例 3 > 00…
閱讀更多...
docker 安裝（一）

docker 安裝（一）

docker的安裝 官方文檔&#xff1a;https://docs.docker.com/manuals/ 卸載舊版 首先如果系統中已經存在舊的docker&#xff0c;則先卸載&#xff1a;yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \dock…
閱讀更多...
C++ STL標準程序庫開發指南學習筆記

C++ STL標準程序庫開發指南學習筆記

一、類模板簡介&#xff1a; 在現今的C標準模板庫中&#xff0c;幾乎所有的東西都被設計為template形式&#xff0c;不支持模板&#xff0c;就無法使用標準程序庫。模板庫可以認為是針對一個或多個尚未明確的類型而編寫一套函數或類型。模板是C的一個新特性。通過使用模板&…
閱讀更多...
【前端素材】推薦優質電商類后臺管理系統網頁Vuesax平臺模板（附源碼）

【前端素材】推薦優質電商類后臺管理系統網頁Vuesax平臺模板（附源碼）

一、需求分析 在線后臺管理系統是指供管理員或運營人員使用的Web應用程序&#xff0c;用于管理和監控網站、應用程序或系統的運行和數據。它通常包括一系列工具和功能&#xff0c;用于管理用戶、內容、權限、數據等。下面是關于在線后臺管理系統的詳細分析&#xff1a; 1、功…
閱讀更多...
前端 css 實現標簽的效果

前端 css 實現標簽的效果

效果如下圖 直接上代碼&#xff1a; <div class"label-child">NEW</div> // css樣式 // 父元素 class .border-radius { position: relative; overflow: hidden; } .label-child { position: absolute; width: 150rpx; height: 27rpx; text-align: cente…
閱讀更多...
JavaScript中的this

JavaScript中的this

在實際應用中&#xff0c;了解 this 的行為是非常重要的&#xff0c;特別是在編寫庫或框架時&#xff0c;或者當你需要在回調函數中訪問特定的上下文時&#xff0c;通常推薦使用箭頭函數或者其他方法來確保 this 的正確指向。 在ES6中&#xff0c;this 的值取決于它是如何被調用…
閱讀更多...
最新文章

Copyright @ 2022~2023