參考資料:用python動手學統計學
? ? ? ? 殘差是表現數據與模型不契合的程度的重要指標。
1、導入庫
# 導入庫
# 用于數值計算的庫
import numpy as np
import pandas as pd
import scipy as sp
from scipy import stats
# 導入繪圖的庫
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
# 用于估計統計模型的庫
import statsmodels.formula.api as smf
import statsmodels.api as sm2、數據準備
# 讀取數據
test_result=pd.read_csv(r"文件路徑")
# 擬合模型
mod_glm=smf.glm('result~hours',data=test_result,family=sm.families.Binomial()).fit()3、皮爾遜殘差
二項式的皮爾遜殘差的計算公式如下:
其中,y為響應變量(二值隨機變量,即考試合格情況),N為試驗次數,為估計的成功概率(由mod_glm.predict()得到的預測值)。
對于每個預測結果,試驗次數都是1,所以皮爾遜殘差如下:
4、皮爾遜殘差的含義
????????皮爾遜殘差的分母中的就是二項分布的方差,它的平方根就是二項分布的標準差。
為殘差。殘差除以分布的標準差,得到的就是皮爾遜殘差。
? ? ? ? 假設N不變,那么當p=0.5時,二項分布的方差Np(1-p)最大。當合格與不合格各占一半時,數據非常分散,此時預測值與實際值之間的差距看起來反而更小(易于接受)。當p=0.9時,預測的結果是基本合格,方差較小,此時預測值與實際值之間的差距看起來反而更大(難以接受)。這就是皮爾遜殘差的含義。
? ? ? ? 皮爾遜殘差的平方和叫作皮爾遜卡方統計量。是模型契合度的指標。
5、計算皮爾遜殘差
????????按計算公式的計算代碼如下:
# 預測的成功概率
pred=mod_glm.predict()
# 響應變量(合格情況)
y=test_result.result
# 皮爾遜殘差
pearson_resid=(y-pred)/np.sqrt(pred*(1-pred))
pearson_resid? ? ? ? 從擬合的模型中直接獲取皮爾遜殘差
mod_glm.resid_pearson結果如下:

? ? ? ? 皮爾遜殘差的平方和即為皮爾遜卡方統計量。
# 方法一
np.sum(mod_glm.resid_pearson**2)
# 方法二
mod_glm.pearson_chi26、模型偏差
????????模型偏差(deviance)是評估模型契合度的指標。模型偏差越大,契合度越差。
? ? ? ? 模型偏差用似然的方式表現了殘差平方和,最大似然法所得的結果等于使得模型偏差最小的參數估計的結果。
? ? ? ? 模型偏差的含義就是廣義線性模型中的殘差平方和。對兩個模型偏差的差值進行檢驗的含義和方差分析相同。按模型偏差的定義,兩個模型偏差的差值近似卡方分布。
????????模型偏差的差值檢驗也叫做似然比檢驗。
????????偏差殘差的平方和就是模型偏差。偏差殘差計算公式相對比較復雜,直接從擬合的模型中獲取即可如下:
# 偏差殘差
mod_glm.resid_deviance
# 模型偏差
np.sum(mod_glm.resid_deviance**2)? ? ? ? 當然和可以模型的summary結果中直接獲取模型偏差。
mod_glm.summary().tables[0]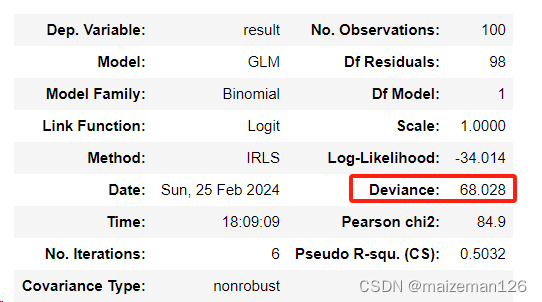
)



之 SQL 映射文件)

+three.js(0.161.0)實現3D可視化地圖)

)

)
)


)


)

