學習參考：

• 動手學深度學習2.0
• Deep-Learning-with-TensorFlow-book
• pytorchlightning

①如有冒犯、請聯系侵刪。
②已寫完的筆記文章會不定時一直修訂修改(刪、改、增)，以達到集多方教程的精華于一文的目的。
③非常推薦上面（學習參考）的前兩個教程，在網上是開源免費的，寫的很棒，不管是開始學還是復習鞏固都很不錯的。

深度學習回顧，專欄內容來源多個書籍筆記、在線筆記、以及自己的感想、想法，佛系更新。爭取內容全面而不失重點。完結時間到了也會一直更新下去，已寫完的筆記文章會不定時一直修訂修改(刪、改、增)，以達到集多方教程的精華于一文的目的。所有文章涉及的教程都會寫在開頭、一起學習一起進步。

1.導數基本含義

古希臘人把一個多邊形分成三角形，并把它們的面積相加，才找到計算多邊形面積的方法。 為了求出曲線形狀（比如圓）的面積，古希臘人在這樣的形狀上刻內接多邊形。 內接多邊形的等長邊越多，就越接近圓。 這個過程也被稱為逼近法（method of exhaustion）。

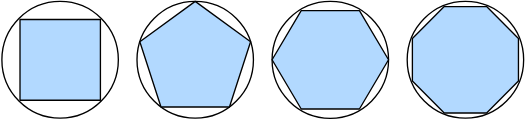
事實上，逼近法就是積分（integral calculus）的起源。 2000多年后，微積分的另一支，微分（differential calculus）被發明出來。 在微分學最重要的應用是優化問題，即考慮如何把事情做到最好。

導數是微積分中的重要概念，它表示函數在某一點處的變化率。具體來說，如果一個函數表示某一物理量隨著時間、空間或其他自變量的變化，那么該函數在某一點的導數就表示該物理量在這一點的變化速率。換句話說，導數告訴函數在某一點處是增加還是減少，以及增加或減少的速率有多快。

其中，?是一個無限接近于零的數。這個定義可以理解為，當 ? 趨近于零時，函數在點 x 處的導數就是函數在點 x 處的切線的斜率。

導數等價符號：

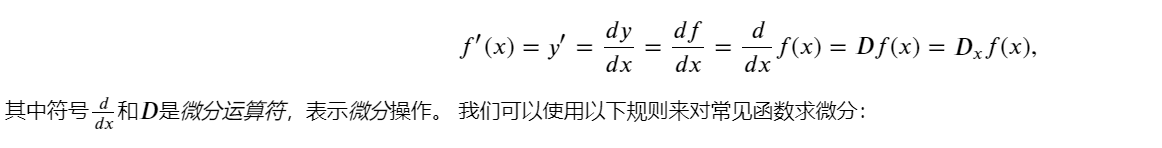
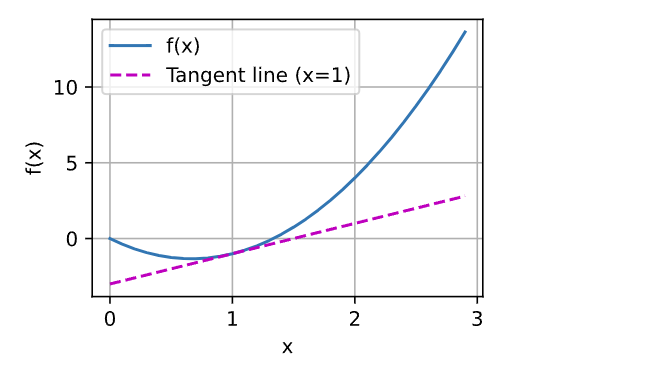
繪制函數 𝑢=𝑓(𝑥) 及其在 𝑥=1處的切線 𝑦=2𝑥?3 ]， 其中系數 2是切線的斜率：

2.基本導數公式

3.偏導數

深度學習中，函數通常依賴于許多變量。 因此，需要將微分的思想推廣到多元函數（multivariate function）上。

偏導數是多元函數的導數概念的推廣，它用于描述一個函數關于其中一個自變量的變化率，而將其他自變量視為常數。對于一個具有多個自變量的函數，其偏導數告訴我們，當其中一個自變量發生變化時，函數值的變化率是多少。

詳細一點說明：

4.梯度

可以連結一個多元函數對其所有變量的偏導數，以得到該函數的梯度（gradient）向量。梯度是一個向量，表示多元函數在給定點處的最大變化率和變化的方向。

函數 𝑓(𝐱) 相對于 𝐱 的梯度是一個包含 𝑛 個偏導數的向量：

梯度告訴函數在某一點的變化率最快的方向。在二維空間中，梯度就是函數的偏導數構成的向量，指向函數增長最快的方向，其大小表示增長的速率。在三維空間中，梯度也是類似的概念，它是一個三維向量，指向函數增長最快的方向。

梯度在優化問題中非常有用，因為在最小化或最大化一個函數時，沿著梯度的方向函數值變化最快，可以幫助找到函數的極小值或極大值。

5.鏈式法則

在深度學習中，多元函數通常是復合（composite）的， 所以難以應用上述任何規則來微分這些函數。 幸運的是，鏈式法則可以被用來微分復合函數。

6.自動微分

深度學習框架通過自動計算導數，即自動微分（automatic differentiation）來加快求導。 實際中，根據設計好的模型，系統會構建一個計算圖（computational graph）， 來跟蹤計算是哪些數據通過哪些操作組合起來產生輸出。 自動微分使系統能夠隨后反向傳播梯度。 這里，反向傳播（backpropagate）意味著跟蹤整個計算圖，填充關于每個參數的偏導數。

自動計算微分的過程示例如下：

import tensorflow as tf# 變量x賦值初始值
x = tf.range(4, dtype=tf.float32)
# 存放梯度的變量,將x轉換為Variable張量，方便更新。
x = tf.Variable(x)
print(x)
# 把所有計算記錄在磁帶上
with tf.GradientTape() as t:# 計算y=計算x和x的點積y = 2 * tf.tensordot(x, x, axes=1)
# 調用磁帶的反向傳播函數自動計算y關于x的每個梯度
x_grad = t.gradient(y, x)
x_grad,y,x

<tf.Variable 'Variable:0' shape=(4,) dtype=float32, numpy=array([0., 1., 2., 3.], dtype=float32)>
(<tf.Tensor: shape=(4,), dtype=float32, numpy=array([ 0.,  4.,  8., 12.], dtype=float32)>,<tf.Tensor: shape=(), dtype=float32, numpy=28.0>,<tf.Variable 'Variable:0' shape=(4,) dtype=float32, numpy=array([0., 1., 2., 3.], dtype=float32)>)

6.1非標量變量的反向傳播

當y不是標量時，向量y關于向量x的導數的最自然解釋是一個矩陣。 對于高階和高維的y和x，求導的結果可以是一個高階張量。

然而，雖然這些更奇特的對象確實出現在高級機器學習中（包括[深度學習中]）， 但當調用向量的反向計算時，我們通常會試圖計算一批訓練樣本中每個組成部分的損失函數的導數。

# 變量x賦值初始值
x = tf.range(4, dtype=tf.float32)
# 存放梯度的變量,將x轉換為Variable張量，方便更新。
x = tf.Variable(x)
print(x)
with tf.GradientTape() as t:y = x * x
t.gradient(y, x)  # 等價于y=tf.reduce_sum(x*x)

6.2分離計算

有時，希望將某些計算移動到記錄的計算圖之外。 例如，假設y是作為x的函數計算的，而z則是作為y和x的函數計算的。 想計算z關于x的梯度，但由于某種原因，希望將y視為一個常數， 并且只考慮到x在y被計算后發揮的作用。

這里可以分離y來返回一個新變量u，該變量與y具有相同的值， 但丟棄計算圖中如何計算y的任何信息。 換句話說，梯度不會向后流經u到x。 因此，下面的反向傳播函數計算z=ux關于x的偏導數，同時將u作為常數處理， 而不是z=xx*x關于x的偏導數。

# 變量x賦值初始值
x = tf.range(4, dtype=tf.float32)
# 存放梯度的變量,將x轉換為Variable張量，方便更新。
x = tf.Variable(x)
print(x)
# 設置persistent=True來運行t.gradient多次
with tf.GradientTape(persistent=True) as t:y = x * xu = tf.stop_gradient(y)z = u * xx_grad = t.gradient(z, x)
print(x_grad)
x_grad == u

<tf.Variable 'Variable:0' shape=(4,) dtype=float32, numpy=array([0., 1., 2., 3.], dtype=float32)>
tf.Tensor([0. 1. 4. 9.], shape=(4,), dtype=float32)
<tf.Tensor: shape=(4,), dtype=bool, numpy=array([ True,  True,  True,  True])>

由于記錄了y的計算結果，可以隨后在y上調用反向傳播， 得到y=x*x關于的x的導數結果查看或者用作其它用途：

t.gradient(y, x)

<tf.Tensor: shape=(4,), dtype=float32, numpy=array([0., 2., 4., 6.], dtype=float32)>

6.3控制流的梯度計算

即使構建函數的計算圖需要通過Python控制流（例如，條件、循環或任意函數調用），仍然可以計算得到的變量的梯度：

def f(a):b = a * 2while tf.norm(b) < 1000:b = b * 2if tf.reduce_sum(b) > 0:c = belse:c = 100 * breturn ca = tf.Variable(tf.random.normal(shape=()))
print(a)
with tf.GradientTape() as t:d = f(a)
d_grad = t.gradient(d, a)
print(d)
d_grad

7.概率

概率是描述隨機事件發生可能性的量度。在數學上，概率通常用一個介于 0 到 1 之間的實數來表示，其中 0 表示不可能事件，1 表示必然事件。例如，擲一枚公正硬幣出現正面的概率為 0.5，即 50% 的可能性。

概率可以通過頻率或基于理論模型來確定。頻率概率是通過觀察事件發生的次數來計算的，當試驗次數趨于無窮時，頻率概率會趨近于一個固定值。理論概率是基于事件的可能性和相關因素來計算的，常用的方法包括古典概率、幾何概率和條件概率等。
概率可以分為幾種不同的類型，主要包括以下幾種：

• 古典概率：也稱為等可能概率，指的是在有限個等可能結果的隨機試驗中，某個事件發生的概率等于該事件發生的可能性除以總的可能性個數。例如，擲一個公正骰子，出現任意一個點數的概率為1/6。
• 幾何概率：幾何概率是指根據幾何形狀和尺寸計算概率的方法，通常用于連續型隨機變量。例如，在一個正方形區域內隨機拋一點，落在某個子區域內的概率與該子區域的面積成正比。
• 條件概率：條件概率是指在給定某個條件下事件發生的概率。如果事件 A 和事件 B 都是隨機事件，且事件 B 的概率大于 0，則事件 A在事件 B 已經發生的條件下發生的概率稱為事件 A 在事件 B 條件下的概率，記作 P(A|B)。
• 貝葉斯概率：貝葉斯概率是指根據先驗概率和新的證據來計算更新后的概率，常用于統計推斷和機器學習中。
• 頻率概率：頻率概率是指根據大量重復實驗中事件發生的相對頻率來計算概率的方法。例如，擲一枚硬幣出現正面的概率可以通過大量重復擲硬幣實驗來估計。

把從概率分布中抽取樣本的過程稱為抽樣（sampling）。 籠統來說，可以把分布（distribution）看作對事件的概率分配。 將概率分配給一些離散選擇的分布稱為多項分布（multinomial distribution）。

7.1基本概率論

檢查骰子的唯一方法是多次投擲并記錄結果， 對于每個骰子，我們將觀察到 {1,…,6} 中的一個值。 對于每個值，一種自然的方法是將它出現的次數除以投擲的總次數， 即此事件（event）概率的估計值。 大數定律（law of large numbers）告訴我們： 隨著投擲次數的增加，這個估計值會越來越接近真實的潛在概率。

%matplotlib inline
import numpy as np
import tensorflow as tf
import tensorflow_probability as tfp
from d2l import tensorflow as d2lfair_probs = tf.ones(6) / 6
counts = tfp.distributions.Multinomial(10, fair_probs).sample(500)
cum_counts = tf.cumsum(counts, axis=0)
estimates = cum_counts / tf.reduce_sum(cum_counts, axis=1, keepdims=True)d2l.set_figsize((6, 4.5))
for i in range(6):d2l.plt.plot(estimates[:, i].numpy(),label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend();

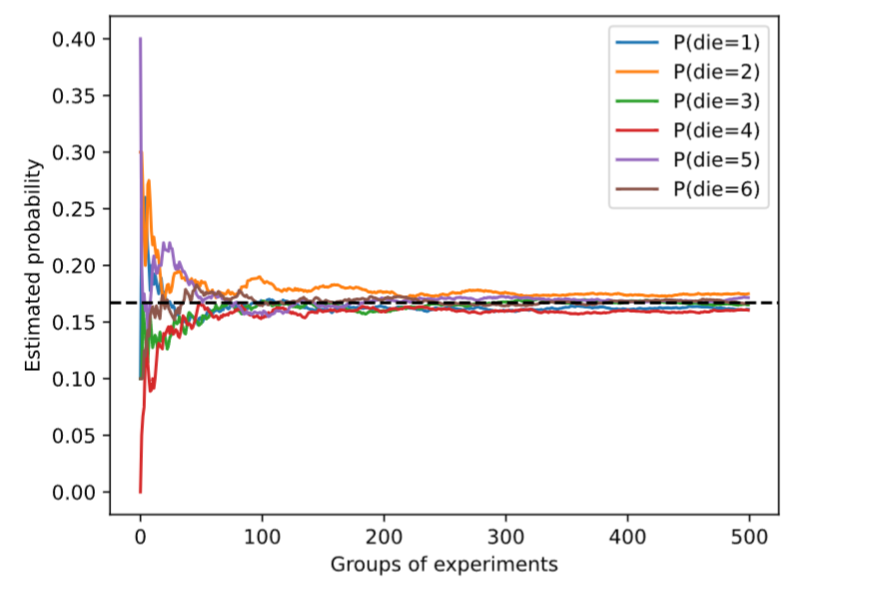
每條實線對應于骰子的6個值中的一個，并給出骰子在每組實驗后出現值的估計概率。 當我們通過更多的實驗獲得更多的數據時，這 6條實體曲線向真實概率收斂。

對骰子進行采樣，可以模擬1000次投擲。 然后，可以統計1000次投擲后，每個數字被投中了多少次。 具體來說，計算相對頻率，以作為真實概率的估計。

counts = tfp.distributions.Multinomial(1000, fair_probs).sample()
counts / 1000

<tf.Tensor: shape=(6,), dtype=float32, numpy=array([0.167, 0.175, 0.143, 0.164, 0.182, 0.169], dtype=float32)>

因為是從一個公平的骰子中生成的數據，每個結果都有真實的概率 1/6 ， 大約是 0.167 ，所以上面輸出的估計值看起來不錯。這也反映了大數定律的有效性。

概率論公理
在處理骰子擲出時，我們將集合 S={1,2,3,4,5,6} 稱為樣本空間（sample space）或結果空間（outcome space）， 其中每個元素都是結果（outcome）。 事件（event）是一組給定樣本空間的隨機結果。
概率（probability）可以被認為是將集合映射到真實值的函數。 在給定的樣本空間 S 中，事件 A 的概率， 表示為 𝑃(A) ，滿足以下屬性：

隨機變量
在概率論和統計學中，隨機變量是一個用來描述隨機現象結果的變量，它可以取多個可能的取值，每個取值對應著一種可能的結果。隨機變量可以是離散的，也可以是連續的。

• 離散隨機變量：離散隨機變量的取值是可數的，通常是整數。例如，拋一次硬幣正面出現的次數就是一個離散隨機變量，可能的取值為 0 或 1。
• 連續隨機變量：連續隨機變量的取值是在一個區間內的實數，取值是不可數的。例如，一個人身高就是一個連續隨機變量，可以在某個范圍內取任意實數值。

請注意，離散（discrete）隨機變量（如骰子的每一面） 和連續（continuous）隨機變量（如人的體重和身高）之間存在微妙的區別。 現實生活中，測量兩個人是否具有完全相同的身高沒有太大意義。 如果我們進行足夠精確的測量，最終會發現這個星球上沒有兩個人具有完全相同的身高。 在這種情況下，詢問某人的身高是否落入給定的區間，比如是否在1.79米和1.81米之間更有意義。 在這些情況下，我們將這個看到某個數值的可能性量化為密度（density）。 高度恰好為1.80米的概率為0，但密度不是0。 在任何兩個不同高度之間的區間，我們都有非零的概率。

7.2處理多個隨機變量

很多時候，會考慮多個隨機變量。 比如，可能需要對疾病和癥狀之間的關系進行建模。 給定一個疾病和一個癥狀，比如“流感”和“咳嗽”，以某個概率存在或不存在于某個患者身上。 需要估計這些概率以及概率之間的關系，以便可以運用推斷來實現更好的醫療服務。

（1）聯合概率

聯合概率（joint probability） 𝑃(𝐴=𝑎,𝐵=𝑏)。 給定任意值 𝑎 和 𝑏 ，聯合概率可以回答： 𝐴=𝑎 和 𝐵=𝑏 同時滿足的概率是多少？ 請注意，對于任何 𝑎 和 𝑏 的取值， 𝑃(𝐴=𝑎,𝐵=𝑏)≤𝑃(𝐴=𝑎)。 這點是確定的，因為要同時發生 𝐴=𝑎 和 𝐵=𝑏 ， 𝐴=𝑎 就必須發生， 𝐵=𝑏 也必須發生（反之亦然）。因此， 𝐴=𝑎 和 𝐵=𝑏同時發生的可能性不大于 𝐴=𝑎 或是 𝐵=𝑏 單獨發生的可能性。

（2）條件概率

聯合概率的不等式帶來一個有趣的比率： 0≤𝑃(𝐴=𝑎,𝐵=𝑏)𝑃(𝐴=𝑎)≤1 。 我們稱這個比率為條件概率（conditional probability）， 并用 𝑃(𝐵=𝑏∣𝐴=𝑎) 表示它：它是 𝐵=𝑏 的概率，前提是 𝐴=𝑎已發生。

（3）貝葉斯定理

使用條件概率的定義，我們可以得出統計學中最有用的方程之一： Bayes定理（Bayes’ theorem）。 根據乘法法則（multiplication rule ）可得到 𝑃(𝐴,𝐵)=𝑃(𝐵∣𝐴)𝑃(𝐴) 。 根據對稱性，可得到 𝑃(𝐴,𝐵)=𝑃(𝐴∣𝐵)𝑃(𝐵) 。 假設 𝑃(𝐵)>0，求解其中一個條件變量，得到：

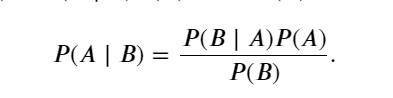
請注意，這里使用緊湊的表示法： 其中 𝑃(𝐴,𝐵) 是一個聯合分布（joint distribution）， 𝑃(𝐴∣𝐵)
是一個條件分布（conditional distribution）。 這種分布可以在給定值 𝐴=𝑎,𝐵=𝑏 上進行求值。

（4）邊際化（邊際概率）

為了能進行事件概率求和，需要求和法則（sum rule）， 即 𝐵 的概率相當于計算 𝐴 的所有可能選擇，并將所有選擇的聯合概率聚合在一起，這也稱為邊際化（marginalization）。 邊際化結果的概率或分布稱為邊際概率（marginal probability） 或邊際分布（marginal distribution）。：

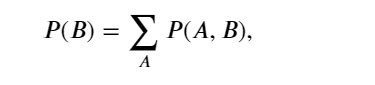
（5）獨立性

依賴（dependence）與獨立（independence）。 如果兩個隨機變量 𝐴 和 𝐵 是獨立的，意味著事件 𝐴
的發生跟 𝐵 事件的發生無關。 在這種情況下，統計學家通常將這一點表述為 𝐴⊥𝐵 。 根據貝葉斯定理，馬上就能同樣得到 𝑃(𝐴∣𝐵)=𝑃(𝐴) 。在所有其他情況下，我們稱 𝐴 和 𝐵 依賴。 比如，兩次連續拋出一個骰子的事件是相互獨立的。 相比之下，燈開關的位置和房間的亮度并不是依賴關系（因為可能存在燈泡壞掉、電源故障，或者開關故障）。

7.3期望與方差

為了概括概率分布的關鍵特征，需要一些測量方法。 一個隨機變量 𝑋的期望（expectation，或平均值（average））表示為

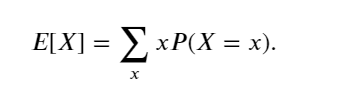
當函數 𝑓(𝑥) 的輸入是從分布 𝑃 中抽取的隨機變量時， 𝑓(𝑥) 的期望值為

在許多情況下，希望衡量隨機變量 𝑋 與其期望值的偏置。這可以通過方差來量化

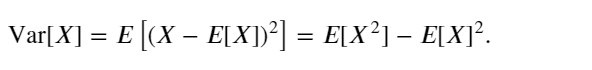
方差的平方根被稱為標準差（standard deviation）。 隨機變量函數的方差衡量的是：當從該隨機變量分布中采樣不同值 𝑥時， 函數值偏離該函數的期望的程度：
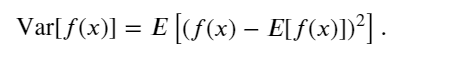