引入：RMQ問題：

什么是RMQ？

顯然，我們無法用前綴維護，因此，我們需要用到線段樹的知識：

什么是線段樹？

線段樹是用一種樹狀結構存儲一個連續區間信息的數據結構

下面我們用圖解釋用它來查詢2--5信息的方式：

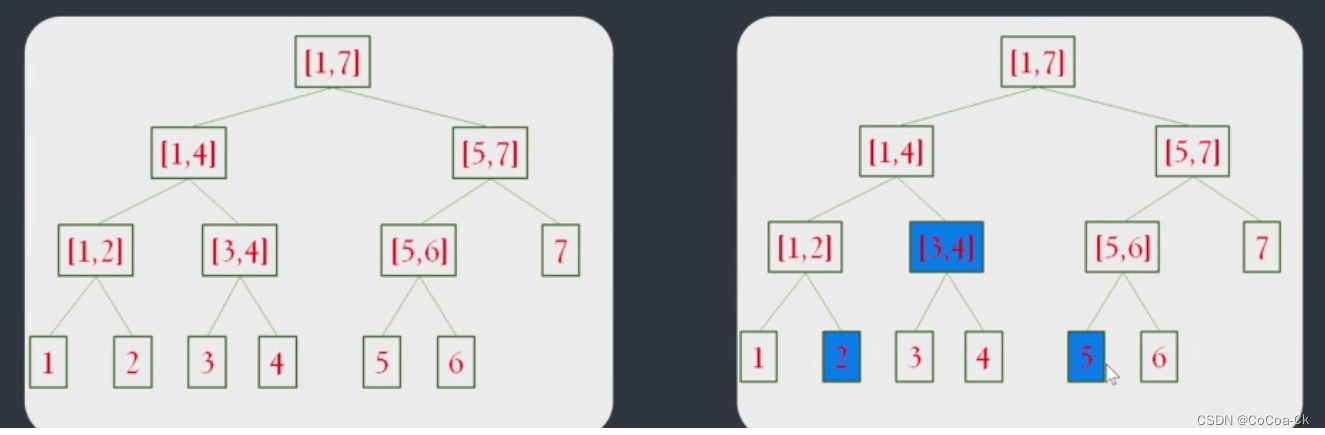
由此，我們可以得到幾點性質：

1.他是一個平衡的二叉樹。

2.對于任意兩個節點，要么完全包含，要么互不相交。

3.任意的線段[a,b]在查詢過程中最多分為log(b-a)個。

4.除建樹外為logn.

我們來一道模板題試試水：

下面是AC代碼：

#include<bits/stdc++.h>
using namespace std;
int n,a[100000];
int tree[4*100000];
void build(int p,int l,int r){if(l==r){tree[p]=a[l];return;}int mid=(l+r)/2;build(p*2,l,mid);build(p*2+1,mid+1,r);tree[p]=tree[p*2+1]+tree[p*2];return;
}
void change(int p,int l,int r,int pos,int num){if(l==r){tree[p]+=num;return;}int mid=(l+r)/2;if(pos<=mid) change(p*2,l,mid,pos,num);else change(p*2+1,mid+1,r,pos,num);tree[p]=tree[2*p]+tree[2*p+1];return;
}
int calc(int p,int l,int r,int x,int y){if(l>=x&&r<=y){return tree[p];}int mid=(l+r)/2;if(y<=mid) return calc(p*2,l,mid,x,y);if(x>mid) return calc(p*2+1,mid+1,r,x,y);return calc(p*2,l,mid,x,mid)+calc(p*2+1,mid+1,r,mid+1,y);
}
int main(){cin>>n;for(int i=1;i<=n;i++) cin>>a[i];build(1,1,n);for(int i=1;i<=n;i++){int x,y,z;cin>>x>>y>>z;if(x==1){change(1,1,n,y,z);}else cout<<calc(1,1,n,y,z);} 
} 

讓我們來看看它的實際應用吧：

區間和問題之懶標記：

我們維護一下節點的兩個信息：

1.sum[i]第i個節點對應的區間和。

2.add[i]第i個節點對應區間整體加上的值并且沒有同步給兒子。

這里我們就知道了為什么叫lazy,該標記僅當被標記的區間有部分被更改才順路把標記下放給它的兒子。這樣就可以減少修改的次數了。

下面是AC代碼：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,a[100010],m;
int tree[4*100010];
int lazy[4*100010];
void build(int p,int l,int r){//建樹 if(l==r){tree[p]=a[l];return;}int mid=(l+r)/2;build(p*2,l,mid);build(p*2+1,mid+1,r);tree[p]=tree[p*2+1]+tree[p*2];return;
}
void pushdown(int p,int l,int r){//lazy標記下移 int mid=(l+r)/2;lazy[p*2]+=lazy[p];lazy[p*2+1]+=lazy[p];tree[p*2]+=lazy[p]*(mid-l+1);//更新子節點的值 tree[p*2+1]+=lazy[p]*(r-mid);lazy[p]=0;//自己因為下移清0 
}
void change(int p,int l,int r,int x,int y,int num){if(x<=l&&r<=y){tree[p]+=num*(r-l+1);lazy[p]+=num;return;}if(lazy[p]!=0){//區間部分修改，需要下移 pushdown(p,l,r);}int mid=(l+r)/2;if(y<=mid) change(p*2,l,mid,x,y,num);if(x>mid) change(p*2+1,mid+1,r,x,y,num);if(x<=mid&&y>mid){change(p*2,l,mid,x,mid,num);change(p*2+1,mid+1,r,mid+1,y,num);}tree[p]=tree[2*p]+tree[2*p+1];return;
}
int calc(int p,int l,int r,int x,int y){if(l>=x&&r<=y){return tree[p];}if(lazy[p]!=0){pushdown(p,l,r);}int mid=(l+r)/2;if(y<=mid) return calc(p*2,l,mid,x,y);if(x>mid) return calc(p*2+1,mid+1,r,x,y);return calc(p*2,l,mid,x,mid)+calc(p*2+1,mid+1,r,mid+1,y);
}
signed main(){cin>>n>>m;for(int i=1;i<=n;i++) scanf("%lld",&a[i]);build(1,1,n);for(int i=1;i<=m;i++){int x,y,k,op;scanf("%lld%lld%lld",&op,&x,&y);if(op==1){scanf("%lld",&k);change(1,1,n,x,y,k);}else cout<<calc(1,1,n,x,y)<<endl;} 
} 

區間平方和問題：

我們還是用lazy標記，不過這時我們維護的sum應該是平方和。那么我們如何維護呢？

因此我們只要維護ai的前綴和即可。

下面是AC代碼：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,a[100010],m,sum[4*100010];
int tree[4*100010];
int lazy[4*100010];
void pushdown(int p,int l,int r);
int calc(int p,int l,int r,int x,int y,int k);
void build(int p,int l,int r){//建樹 if(l==r){tree[p]=a[l]*a[l];sum[p]=a[l];return;}int mid=(l+r)/2;build(p*2,l,mid);build(p*2+1,mid+1,r);tree[p]=tree[p*2+1]+tree[p*2];sum[p]=sum[p*2+1]+sum[p*2+1];return;
}
void pushdown(int p,int l,int r){//lazy標記下移 int mid=(l+r)/2;lazy[p*2]+=lazy[p];lazy[p*2+1]+=lazy[p];tree[p*2]+=2*lazy[p]*(sum[2*p])+lazy[p]*lazy[p]*(mid-l+1);//更新子節點的值 tree[p*2+1]+=2*lazy[p]*(sum[2*p+1])+lazy[p]*lazy[p]*(r-mid);sum[p*2]+=lazy[p]*(mid-l+1);sum[p*2+1]+=lazy[p]*(r-mid);lazy[p]=0;//自己因為下移清0 
}
void change(int p,int l,int r,int x,int y,int num){if(x<=l&&r<=y){tree[p]+=2*num*(sum[p])+num*num*(r-l+1);sum[p]+=num*(r-l+1);lazy[p]+=num;return;}if(lazy[p]!=0){//區間部分修改，需要下移 pushdown(p,l,r);}int mid=(l+r)/2;if(y<=mid) change(p*2,l,mid,x,y,num);if(x>mid) change(p*2+1,mid+1,r,x,y,num);if(x<=mid&&y>mid){change(p*2,l,mid,x,mid,num);change(p*2+1,mid+1,r,mid+1,y,num);}tree[p]=tree[2*p]+tree[2*p+1];sum[p]=sum[2*p]+sum[2*p+1];return;
}
int calc(int p,int l,int r,int x,int y,int k){if(l>=x&&r<=y){if(k==1) return tree[p];else return sum[p];}if(lazy[p]!=0){pushdown(p,l,r);}int mid=(l+r)/2;if(y<=mid) return calc(p*2,l,mid,x,y,k);if(x>mid) return calc(p*2+1,mid+1,r,x,y,k);return calc(p*2,l,mid,x,mid,k)+calc(p*2+1,mid+1,r,mid+1,y,k);
}
signed main(){cin>>n>>m;for(int i=1;i<=n;i++) scanf("%lld",&a[i]);build(1,1,n);for(int i=1;i<=m;i++){int x,y,k,op;scanf("%lld%lld%lld",&op,&x,&y);if(op==1){scanf("%lld",&k);change(1,1,n,x,y,k);}else cout<<calc(1,1,n,x,y,1)<<endl;} 
}