一、聚類模型簡介

“物以類聚， 人以群分”，所謂的聚類，就是將樣本劃分為由類似的對象組成的多個類的過程。聚類后，我們可以更加準確的在每個類中單獨使用統計模型進行估計、分析或預測，也可以探究不同類之間的相關性和主要差異。

聚類和分類的區別：分類是已知類別的，聚類未知。

注：聚類模型一般有三種算法，K-means++法、系統層次法和DBSCAN法。

二、適用賽題

只有一對數據，要求將數據分為幾類，類數不定。如有全國34個省的關于消費水平的幾個指標，現要求將34個省分為幾類分析。

三、模型流程

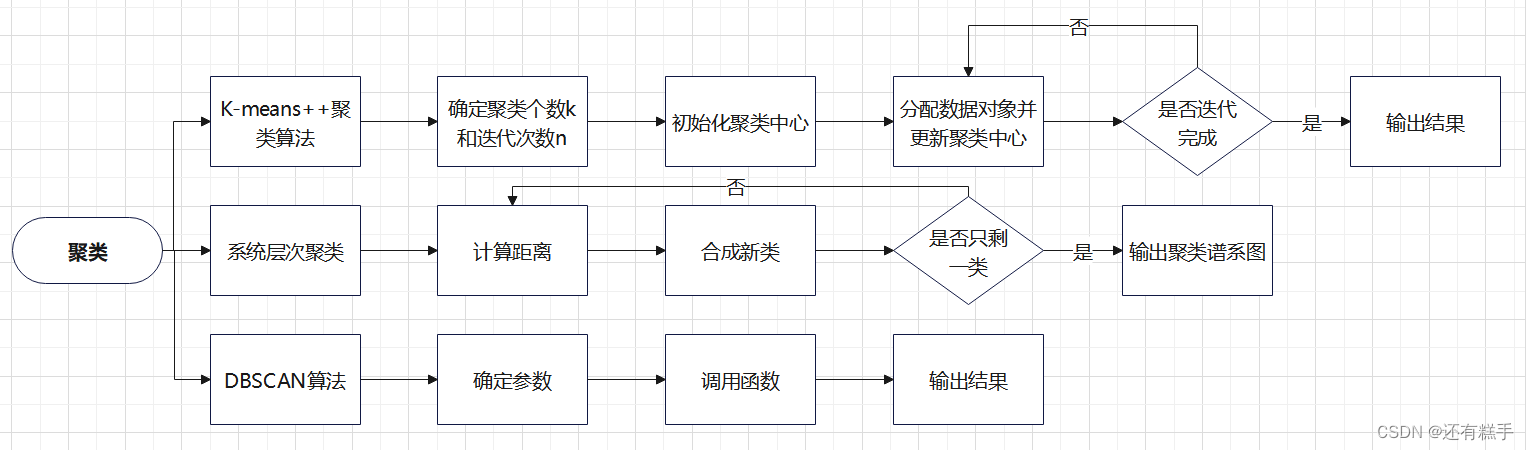
四、流程解析

1.K-means++聚類算法

K-means++算法是由K-means算法改進而來，對于K-means算法

優點

• 算法簡單、快速
• 對處理大數據集，該算法是相對高效率的

缺點

• 要求用戶必須事先給出要生成的簇的數目K
• 對初值敏感
• 對于孤立點數據敏感

而K-means++算法可解決后兩個缺點。

①確定參數

聚類個數也就是簇的個數，也就是像分為多少個類。

迭代次數是指數據每經過一次迭代，都會有不同的數據進入不同的類，直到達到最大迭代次數，一般10次后，每次迭代后類中的數據就不會改變了。

②初始化聚類中心

這里就是優化的地方。K-means算法在初始化的時候，只是隨機地選擇K個數據對象作為初始的聚類中心。而K-means++算法選擇初始聚類中心的基本原則是：初始的聚類中心之間的相互距離要盡可能的遠。

具體流程如下

1. 隨機選取一個樣本作為第一個聚類中心
2. 計算每個樣本與當前已有聚類中心的最短距離（即與最近一個聚類中心的距離），這個值越大，表示被選取作為聚類中心的概率較大。最后，用輪盤法（依據概率大小來進行抽選）選出下一個聚類中心
3. 重復步驟二，直到選出K個聚類中心。選出初始點后，就繼續使用標準的K-means算法了

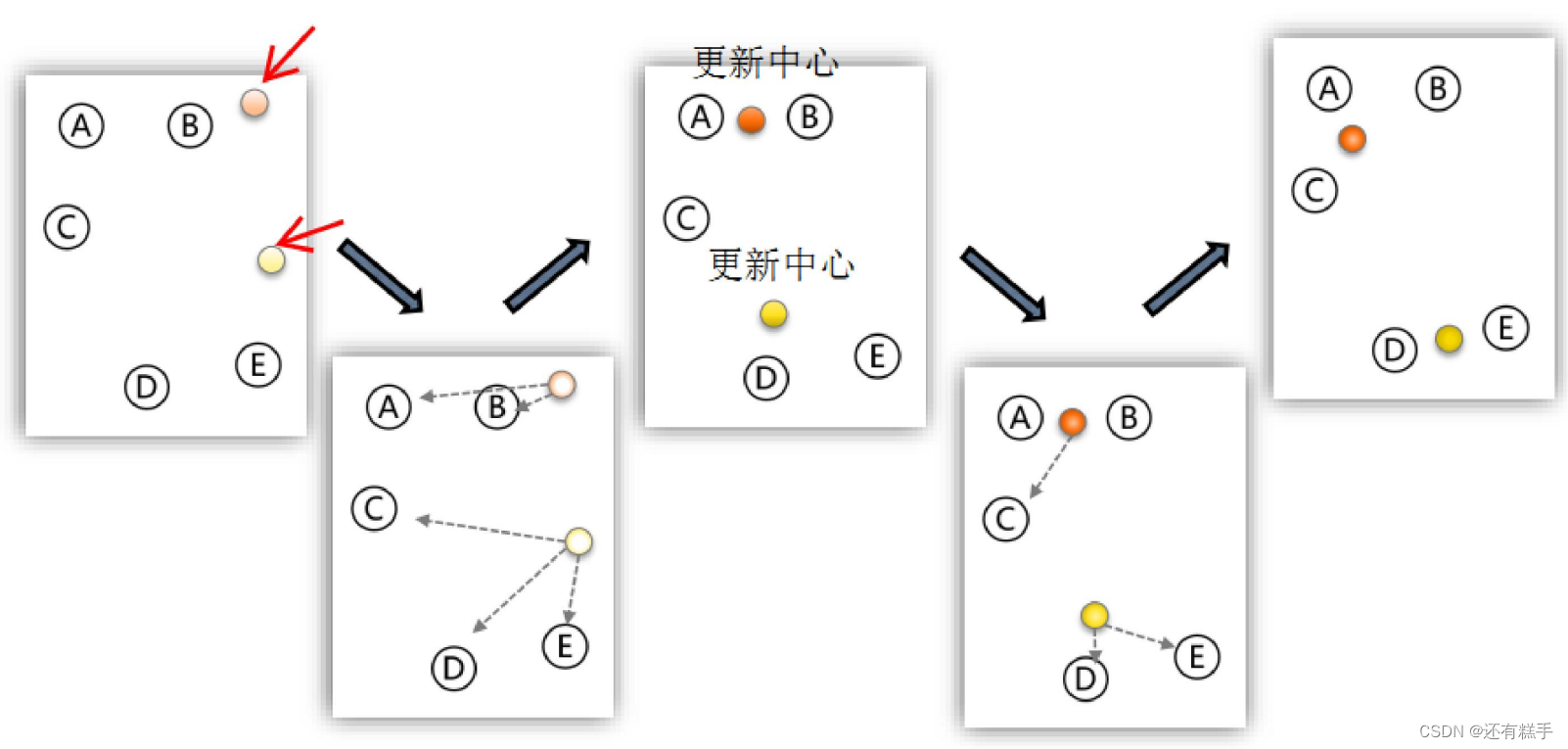
③分配和更新

分配數據對象是指計算其余的各個數據對象到這K個初始聚類中心的距離，把數據對象劃歸到距離它最近的那個中心所處在的簇類中變成一個新類。

更新聚類中心是指重新計算出新類的中心，新的中心就是所有數據對象的重心。

下面是K-means算法的演示圖

④輸出結果

當完成迭代次數后，得到結果。

⑤補充

聚類的個數K值怎么定？

答：分幾類主要取決于個人的經驗與感覺，通常的做法是多嘗試幾個K值,看分成幾類的結果更好解釋，更符合分析目的等。

數據的量綱不一致怎么辦？

答：如果數據的量綱不一樣，那么算距離時就沒有意義。例如:如果X1單位是米，X2單位是噸，用距離公式計算就會出現“米的平方”加上“噸的平方”再開平方，最后算出的東西沒有數學意義，這就有問題了。這就需要標準化。

這里還是推薦使用SPSS軟件進行操作。

2.系統層次聚類

系統聚類的合并算法通過計算兩類數據點間的距離，對最為接近的兩類數據點進行組合，并反復迭代這一過程，直到將所有數據點合成一類，并生成聚類譜系圖。

①計算距離

這里根據問題看是求誰的距離，一般是樣品之間距離，也有可能是求指標之間的距離。數據的一般格式如下圖

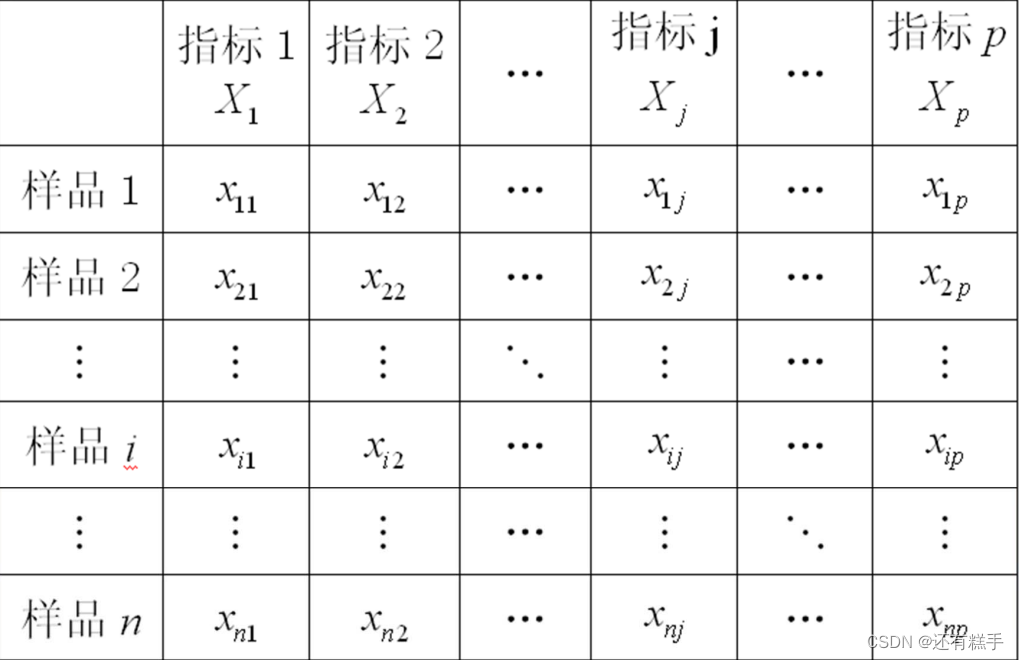
樣品與樣品之間的常用距離（樣品i與樣品j）

指標與指標之間的常用“距離”（指標i與指標j）

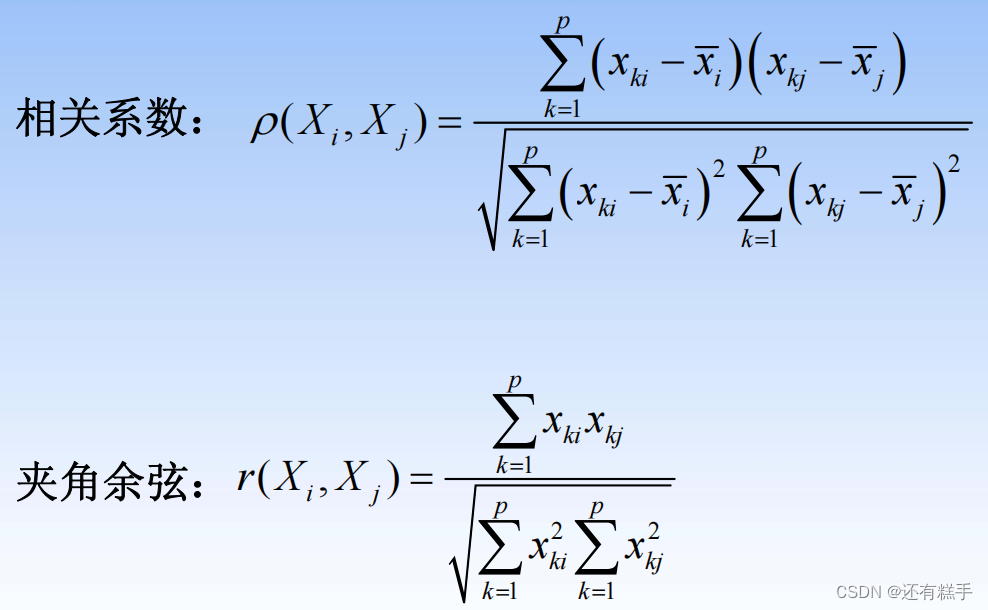
最開始的時候，將每個數據對象看作一類，計算兩兩之間的最小距離。后面是計算類與類之間的兩兩最小距離。

類與類之間的常用距離

• 由一個樣品組成的類是最基本的類，如果每一類都由一個樣品組成，那么樣品間的距離就是類間距離
• 如果某一類包含不止一個樣品，那么就要確定類間距離，類間距離是基于樣品間距離定義的，大致有如下幾種定義方式：

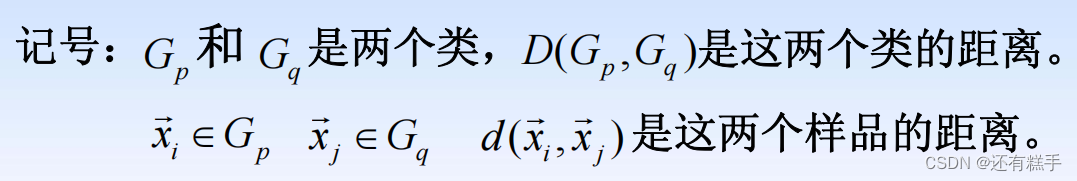
• 最短距離法（Nearest Neighbor）:

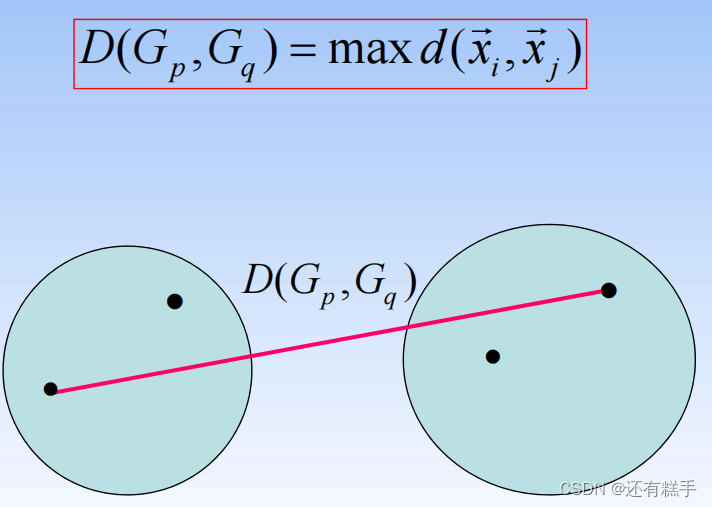
• 組間平均連接法（Between-group Linkage）：

• 組內平均連接法（Within-group Linkage）：

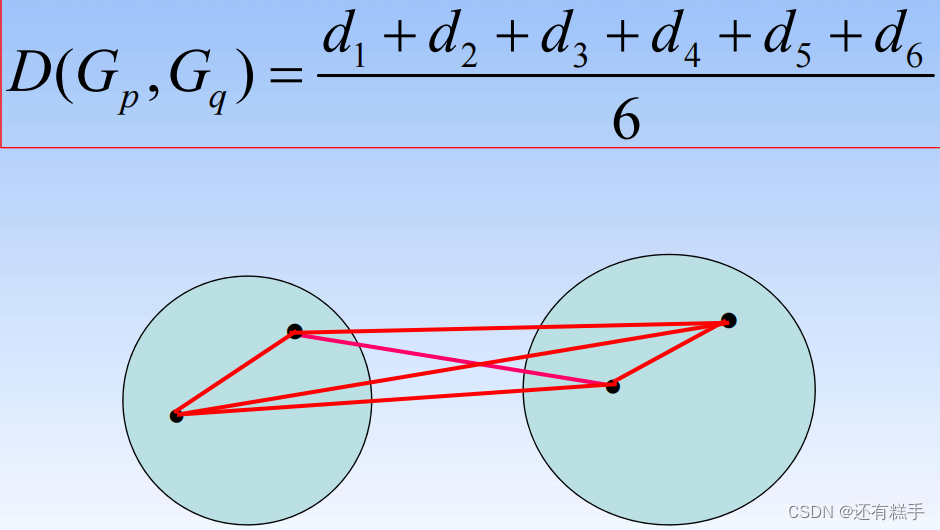
• 重心法（Centroid clustering）：

②合成新類

將距離最小的兩個類合并成一個新類。

③迭代完成

重復計算距離、合成新類，直到最后只剩下一類也就是所有類合并成一類。

④聚類譜系圖

下面就是一個聚類譜系圖

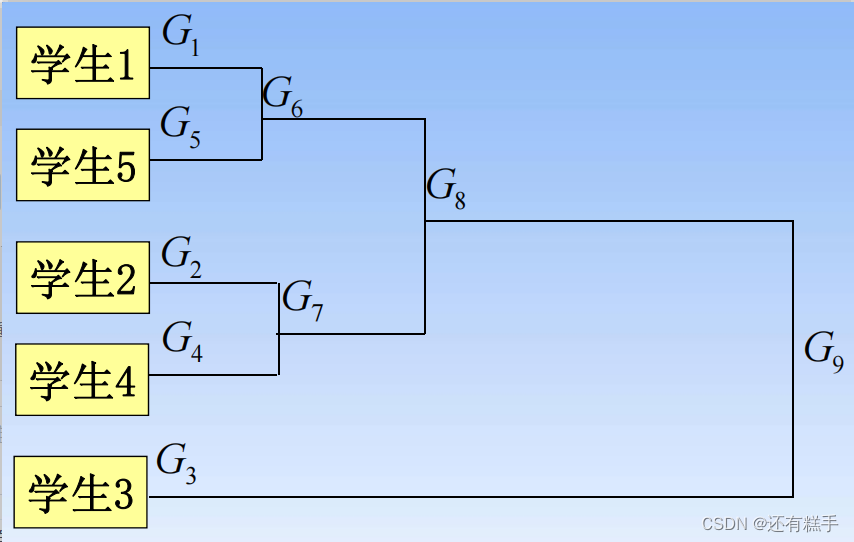
要分成幾類只需要畫豎線即可，有幾個交點就有幾個類，如下圖

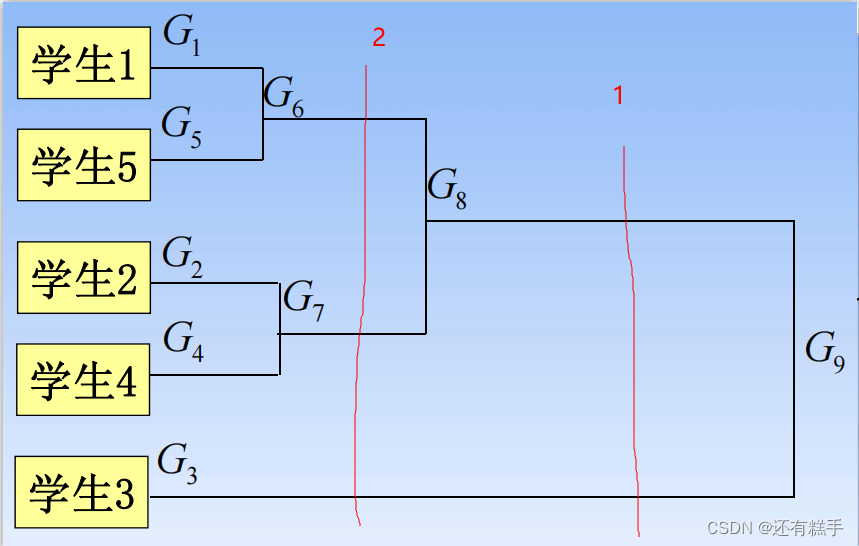
按照1分類就有兩類，按照2分類就有三類。

⑤補充

那劃成多少類才是最合適的？

肘部法則（Elbow Method）：通過圖形大致的估計出最優的聚類數量。

首先介紹

然后得到如下圖

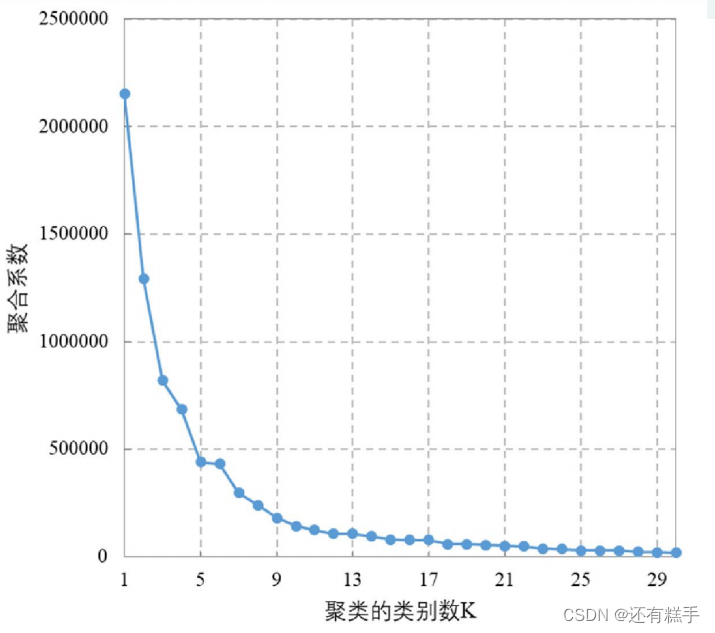
在下降趨勢趨緩的時候選擇，上圖就選擇K = 5。

這里還是推薦使用SPSS軟件進行操作。

3.DBSCAN法

DBSCAN（Density-based spatial clustering of applicationswith noise）是Martin Ester，Hans- PeterKriegel等人于1996年提出的一種基于密度的聚類方法，聚類前不需要預先指定聚類的個數，生成的簇的個數不定（和數據有關）。該算法利用基于密度的聚類的概念，即要求聚類空間中的一定區域內所包含對象（點或其他空間對象）的數目不小于某一給定閾值。該方法能在具有噪聲的空間數據庫中發現任意形狀的簇，可將密度足夠大的相鄰區域連接，能有效處理異常數據。

①確定參數

需要設置的參數

• 半徑：Eps
• 點數：MinPts

DBSCAN算法將數據點分為三類

• 核心點：在半徑Eps內含有不少于MinPts數目的點
• 邊界點：在半徑Eps內點的數量小于MinPts，但是落在核心點的鄰域內
• 噪音點：既不是核心點也不是邊界點的點

舉個例子

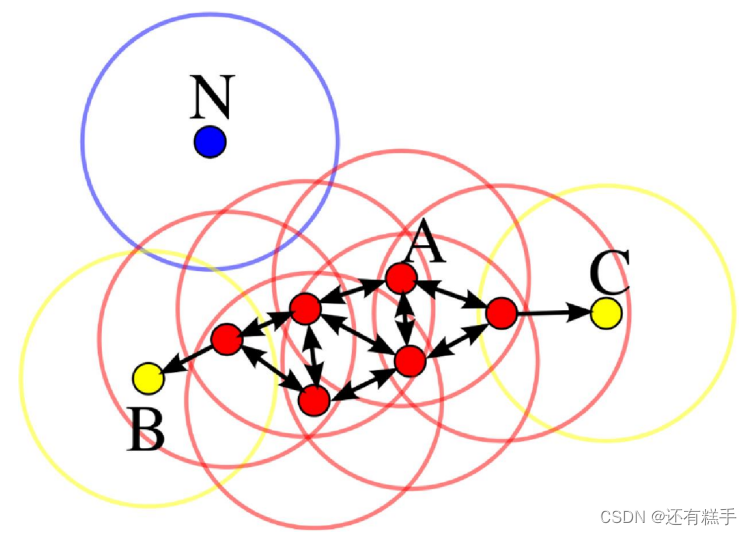
在這幅圖里，MinPts = 4，點A和其他紅色點是核心點，因為它們的Eps-鄰域（圖中紅色圓圈）里包含最少4個點（包括自己），由于它們之間相互相可達，它們形成了一-個聚類。點B和點C不是核心點，但它們可由A經其他核心點可達，所以也和A屬于同一個聚類。點N是局外點，它既不是核心點，又不由其他點可達。

②調用函數

MATLAB在2019a版本中正式加入了自己的dbscan函數，內置函數的運行效率更高。具體使用方法可以查閱MATLAB官網。

③補充

DBSCAN法優缺點

優點

• 基于密度定義，能處理任意形狀和大小的簇
• 可在聚類的同時發現異常點
• 與K-means比較起來，不需要輸入要劃分的聚類個數

缺點

• 對輸入參數Eps和Minpts敏感，確定參數困難
• 由于DBSCAN算法中，變量Eps和Minpts是全局唯一的，當聚類的密度不均勻時，聚類距離相差很大時，聚類質量差
• 當數據量大時，計算密度單元的計算復雜度大

建議

• 只有兩個指標，且你做出散點圖后發現數據表現得很“DBSCAN"，這時候你再用DBSCAN進行聚類
• 其他情況下，全部使用系統聚類吧。K-means++也可以用，不過用了的話論文上可寫的東西比較少