題目

給定一個包含非負整數的數組?nums?，返回其中可以組成三角形三條邊的三元組個數。

示例 1:

輸入: nums = [2,2,3,4]
輸出: 3
解釋:有效的組合是: 
2,3,4 (使用第一個 2)
2,3,4 (使用第二個 2)
2,2,3

示例 2:

輸入: nums = [4,2,3,4]
輸出: 4

提示:

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000

思路

題目判斷三角形，首先我們需要回顧一個小學知識點，三角形的兩邊和是要大于第三邊的，所以按常理講拿到三個數后需要來回判斷三次，而直接暴力枚舉的話，會大大增加時間復雜度，這里首先就可以做一個優化，先把三個數從小到大排，這樣只用判斷一次即可。

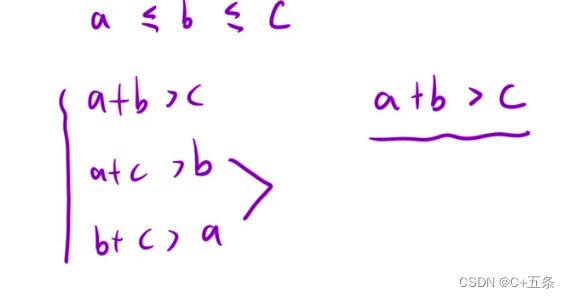
暴力枚舉三次for循環來依次遍歷，復雜度為n^3。明顯不可取。

通過上述小小優化可以先對數組進行一次排序，讓其先變的有序，有序后更方便進行枚舉。

此時可以利用雙指針（這里是三指針）通過單調性來對數據進行遍歷。

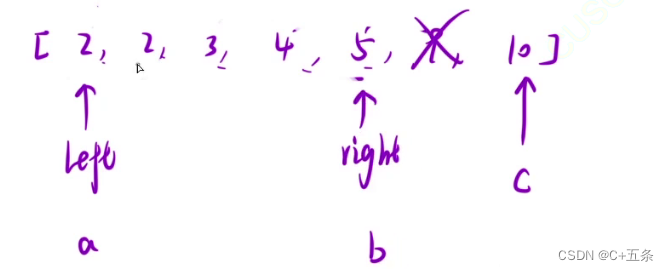
上圖為例，先固定出一個最大的數作為c，然后讓其他數依次組合來進行遍歷，最左為a最右為b，滿足的情況和為sum。

初步判斷a+b>c，所以符合條件，同時可以得出a往右到b之間所有的數相加都滿足此條件，b直接--左移。sum+=b-a。

?此時right指向的數為5，此時判斷a+b<c,此時也可以得出a往右到b之間所有的數相加都不滿足此條件，因為此時b是這個區間中的最大數，b都不滿足，比b小的自然也不滿足，left++向右移動一位。

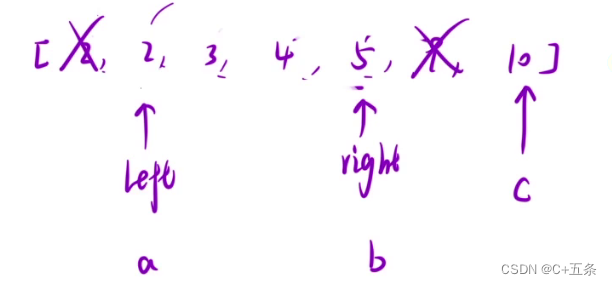
然后依次重復此過程，直到left和right相遇，此時c為10的情況就遍歷完成，然后c--,a b分別重置。

題解

class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(),nums.end());int a=0,b=nums.size()-2,c=nums.size()-1;int sum=0;while(c>=2){while(a<b){if(nums[a]+nums[b]>nums[c]){sum+=(b-a);--b;}else{++a;}}--c;a=0;b=c-1;}return sum;}
};

?